【树DP】2021ICPC南京 H
Problem - H - Codeforces
题意:
思路:
这题应该算是铜牌题
铜牌题 = 简单算法 + 基础思维
简单复盘一下思路
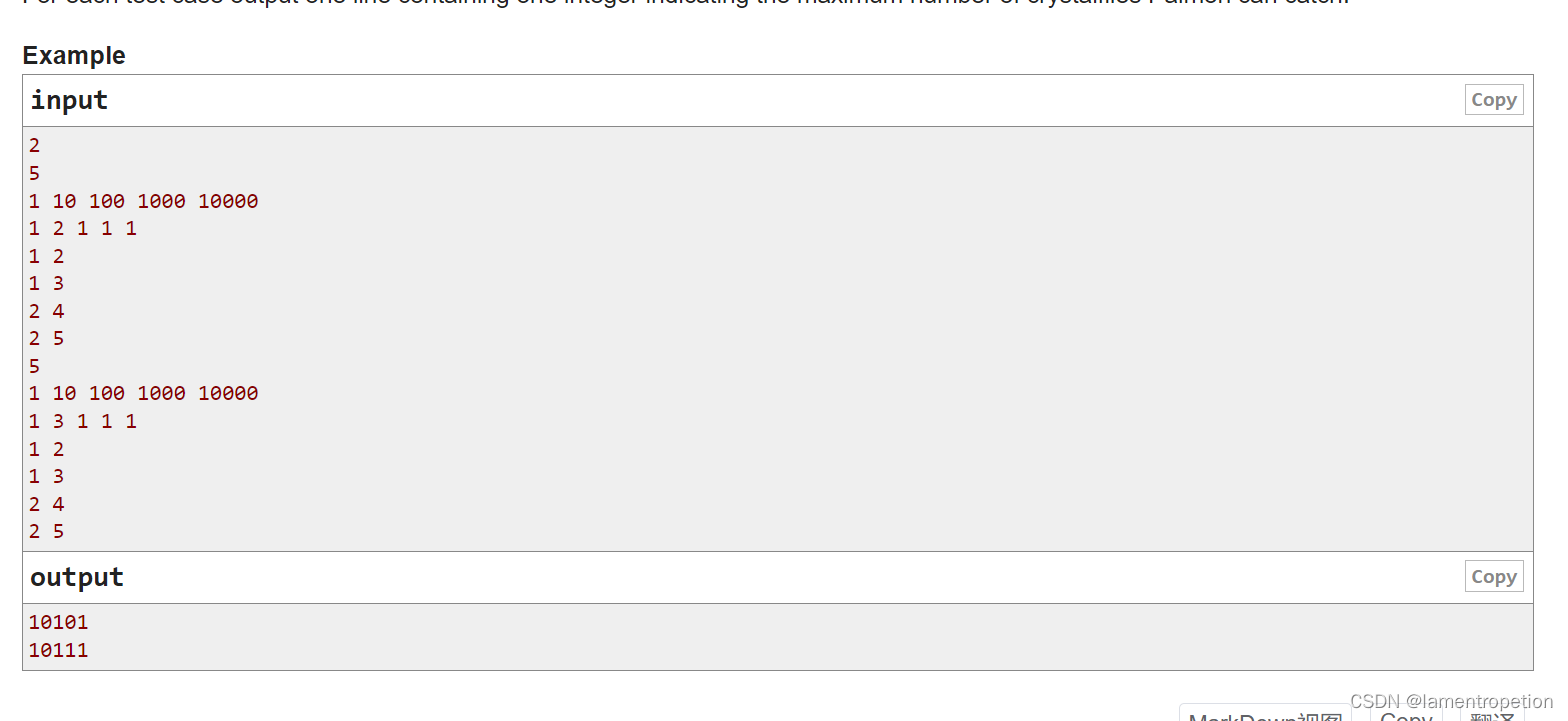
首先,我们发现有个很特殊的条件: ti <= 3
然后看一下样例:
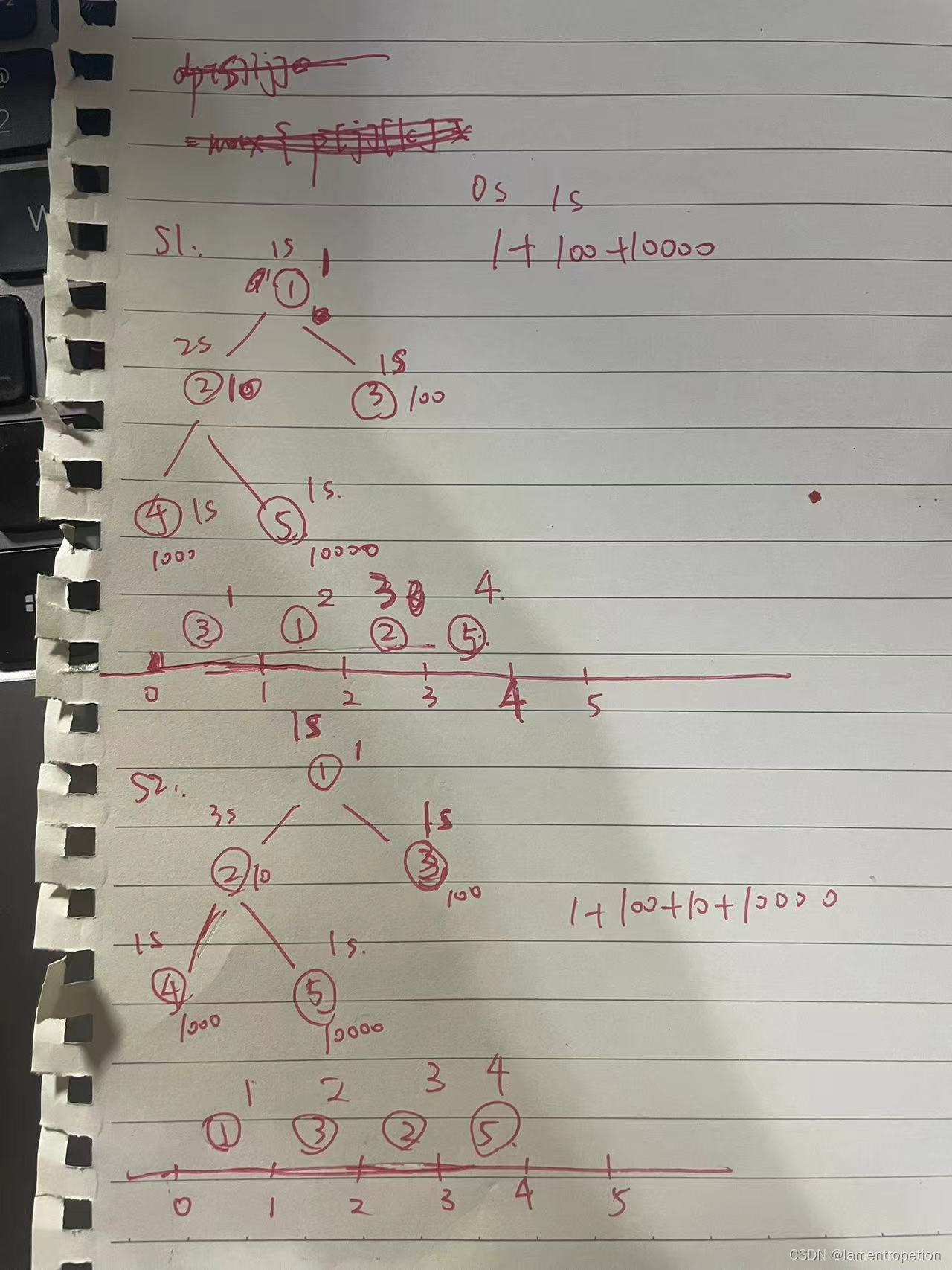
注意到,对于一个结点 u ,如果它的所有子节点中没有 tv = 3的,那么就肯定是沿着一棵子树走到底,然后去走剩下的子树
如果所有子节点中有 tv = 3的,那么可以先走到某个子节点,然后再走到这个 tv = 3的结点
注意到了子问题,那么很自然地去考虑树DP
注意到子问题可以分类成不算结点u 和 算结点u, 因此可以这样设计状态
设 dp[u] 为没有走过结点 u的这棵子树的贡献
然后考虑转移
因为 ti <= 3, 考虑在转移的时候暴力分讨
因为怎么转移和这些子节点中是否存在 tv = 3的结点有关,那么考虑先去把这些结点遍历一遍,看看是否存在,然后去转移
如果存在,那么就是先走到某个结点,再走到这个tv = 3的结点
考虑枚举这个“某个结点”,注意到tv = 3的结点可能会有多个,我们贪心地保留av最大的那个,这个可以考虑用multiset维护
为了计算贡献,我们设sum[u]表示所有子节点的 dp[v] 之和
此时的贡献为:
dp[u] = max{sum[u] - dp[v] + sum[v] + a[v] + *rbegin()}
然后考虑不存在tv = 3的结点,那么就是一次性走到底,再去遍历其他结点,此时贡献为 sum[u] + mx,其中 mx 为所有子节点中最大的 a[v]
为了防止出问题,我们在原来的multiset中先插入 -Inf
Code:
#include <bits/stdc++.h>#define int long longusing i64 = long long;constexpr int N = 1e5 + 10;
constexpr int M = 1e5 + 10;
constexpr int P = 2e2 + 10;
constexpr i64 Inf = 1e18;
constexpr int mod = 1e9 + 7;
constexpr double eps = 1e-6;std::vector<int> adj[N];int n;
int a[N], t[N];
int dp[N], sum[N];void dfs(int u, int fa) {std::multiset<int> S;int mx = 0;for (auto v : adj[u]) {if (v == fa) continue;dfs(v, u);sum[u] += dp[v];mx = std::max(mx, a[v]);if (t[v] == 3) S.insert(a[v]);}dp[u] = sum[u] + mx;S.insert(-0x3f3f3f3f);for (auto v : adj[u]) {if (v == fa) continue;if (t[v] == 3) S.erase(S.find(a[v]));dp[u] = std::max(dp[u], sum[u] - dp[v] + sum[v] + a[v] + (*S.rbegin()));if (t[v] == 3) S.insert(a[v]);}
}
void solve() {std::cin >> n;for (int i = 1; i <= n; i ++) {sum[i] = dp[i] = 0;adj[i].clear();}for (int i = 1; i <= n; i ++) {std::cin >> a[i];}for (int i = 1; i <= n; i ++) {std::cin >> t[i];}for (int i = 1; i <= n - 1; i ++) {int u, v;std::cin >> u >> v;adj[u].push_back(v);adj[v].push_back(u);}dfs(1, -1);std::cout << dp[1] + a[1] << "\n";
}
signed main() {std::ios::sync_with_stdio(false);std::cin.tie(nullptr);int t = 1;std::cin >> t;while (t--) {solve();}return 0;
}相关文章:

【树DP】2021ICPC南京 H
Problem - H - Codeforces 题意: 思路: 这题应该算是铜牌题 铜牌题 简单算法 基础思维 简单复盘一下思路 首先,我们发现有个很特殊的条件: ti < 3 然后看一下样例: 注意到,对于一个结点 u &#…...
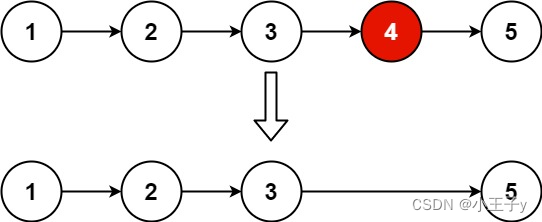
Leedcode19. 删除链表的倒数第 N 个结点
给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。 输入:head [1,2,3,4,5], n 2 输出:[1,2,3,5] 示例 2: 输入:head [1], n 1 输出:[] 示例 3: 输入࿱…...
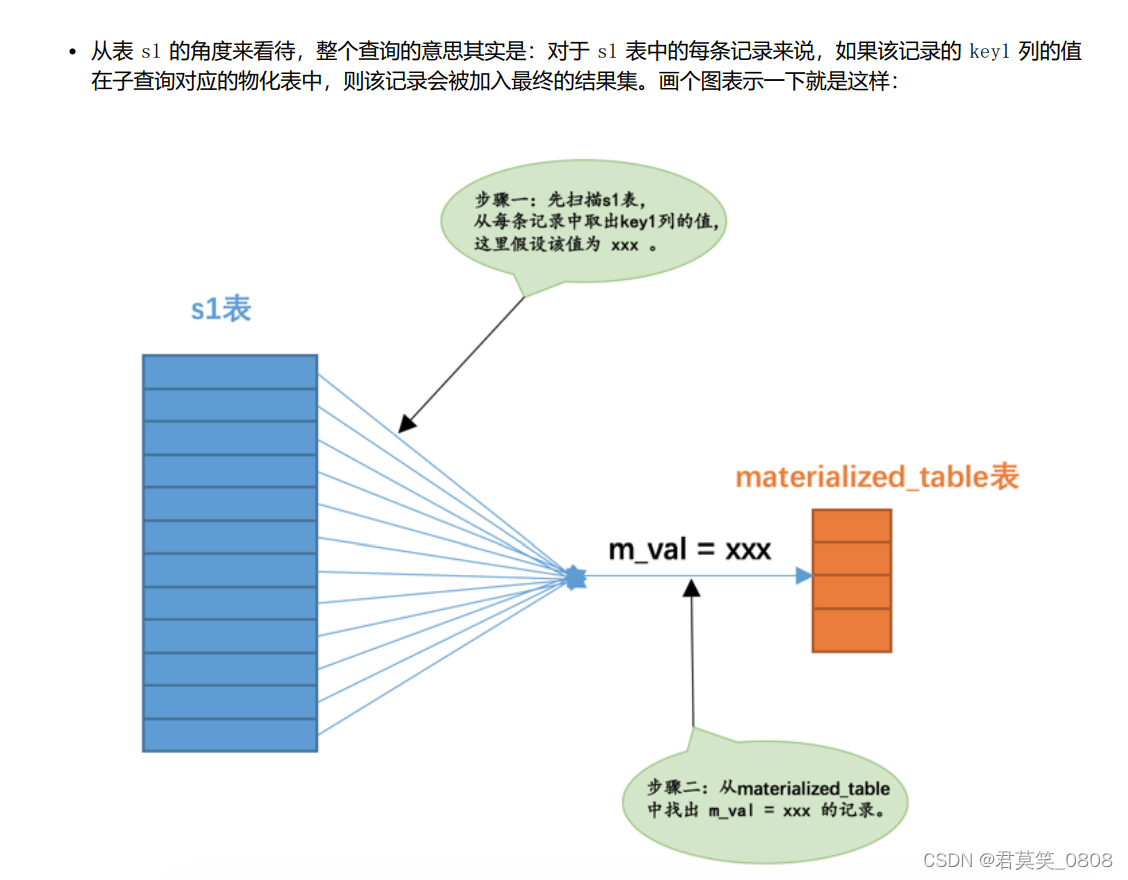
Mysql-索引查询相关
一、单表查询 1.1 二级索引为null 不论是普通的二级索引,还是唯一二级索引,它们的索引列对包含 NULL 值的数量并不限制,所以我们采用key IS NULL 这种形式的搜索条件最多只能使用 ref 的访问方法,而不是 const 的访问方法 1.2 c…...

C++ Pimpl
Pimpl(Pointer to implementation,指向实现的指针) 是一种减少代码依赖和编译时间的C编程技巧,其基本思想是将一个外部可见类(visible class)的实现细节(一般是所有私有的非虚成员)放在一个单独的实现类(implementation class)中&…...

rust学习-类型转换
基本类型转换 // 不显示类型转换产生的溢出警告。 #![allow(overflowing_literals)]fn main() {let decimal 65.4321_f32;// 错误!不提供隐式转换// let integer: u8 decimal;// 可以显式转换let integer decimal as u8;let character integer as char;println…...
算法通过村第四关-栈青铜笔记|手写栈操作
文章目录 前言1. 栈的基础概要1.1 栈的特征1.2 栈的操作1.3 Java中的栈 2. 栈的实现(手写栈)2.1 基于数组实现2.2 基于链表实现2.3 基于LinkedList实现 总结 前言 提示:我自己一个人的感觉很好 我并不想要拥有你 除非你比我的独处更加宜人 --…...

Python计算加速利器
迷途小书童的 Note 读完需要 6分钟 速读仅需 2 分钟 1 简介 Python 是一门应用非常广泛的高级语言,但是,长久以来,Python的运行速度一直被人诟病,相比 c/c、java、c#、javascript 等一众高级编程语言,完全没有优势。 那…...
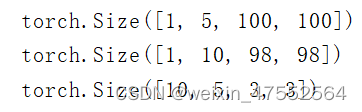
PyTorch 深度学习实践 第10讲刘二大人
总结: 1.输入通道个数 等于 卷积核通道个数 2.卷积核个数 等于 输出通道个数 1.单通道卷积 以单通道卷积为例,输入为(1,5,5),分别表示1个通道,宽为5,高为5。假设卷积核大小为3x3,…...

Linux特殊指令
目录 1.dd命令 2.mkfs格式化 3.df命令 4.mount实现硬盘的挂载 5.unshare 1.dd命令 dd命令可以用来读取转换并输出数据。 示例一: if表示infile,of表示outfile。这里的/dev/zero是一个特殊文件,会不断产生空白数据。 bs表示复制一块的大…...

MPI之主从模式的一般编程示例
比如,我们可以选举0号进程为master进程,其余进程为slaver进程 #include "mpi.h" #include <unistd.h> #include <iostream>int main(int argc, char *argv[]) {int err MPI_Init(&argc,&argv);int rank,size;MPI_Comm_r…...

基于野狗算法优化的BP神经网络(预测应用) - 附代码
基于野狗算法优化的BP神经网络(预测应用) - 附代码 文章目录 基于野狗算法优化的BP神经网络(预测应用) - 附代码1.数据介绍2.野狗优化BP神经网络2.1 BP神经网络参数设置2.2 野狗算法应用 4.测试结果:5.Matlab代码 摘要…...

C语言面向对象的编程思想
面向对象编程 面向对象编程Object-Oriented Programming,OOP) 作为一种新方法,其本质是以建立模型体现出来的抽象思维过程和面向对象的方法。模型是用来反映现实世界中事物特征的。任何一个模型都不可能反映客观事物的一切具体特征࿰…...

MPI之非阻塞通信中通信完成检测接口简介
在之前的文章中,简单的写了一个非阻塞的通信代码介绍最最基本的使用: int main(int argc, char *argv[]) {int err MPI_Init(&argc,&argv);int rank,size;MPI_Comm_rank(MPI_COMM_WORLD,&rank);MPI_Comm_size(MPI_COMM_WORLD, &size);…...
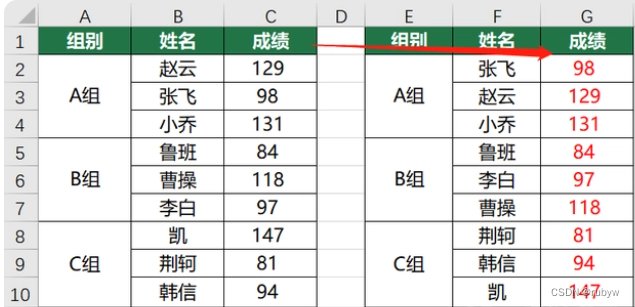
Excel:如何实现分组内的升序和降序?
一、POWER 1、构建辅助列D列,在D2单元格输入公式: -POWER(10,COUNTA($A$2:A2)3)C2 2、选中B1:D10,注意不能宣导A列的合并单元格,进行以下操作: 3、删除辅助列即可 二、COUNTA 第一步,D2建立辅助列…...
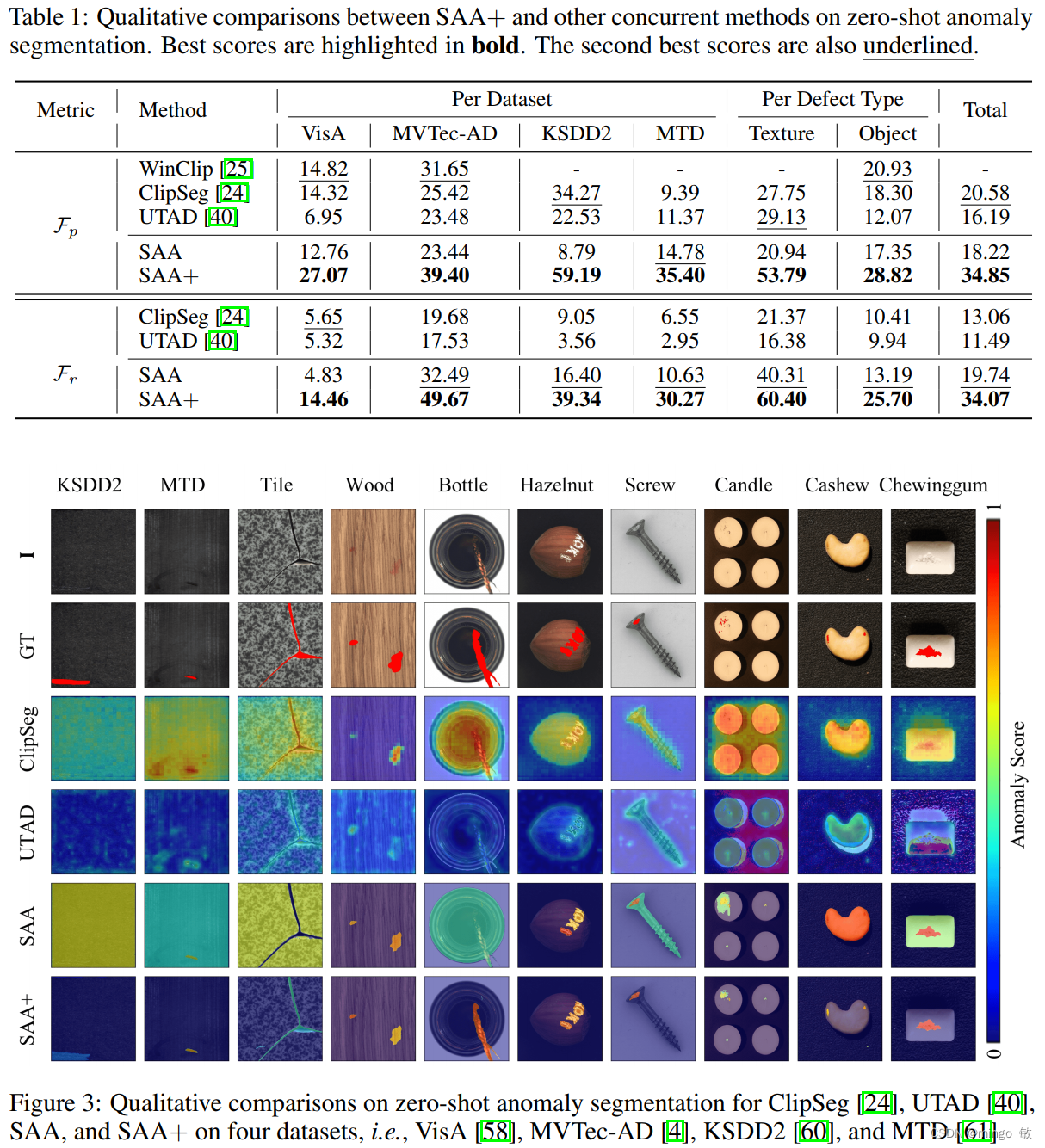
深度学习论文: Segment Any Anomaly without Training via Hybrid Prompt Regularization
深度学习论文: Segment Any Anomaly without Training via Hybrid Prompt Regularization Segment Any Anomaly without Training via Hybrid Prompt Regularization PDF: https://arxiv.org/pdf/2305.10724.pdf PyTorch代码: https://github.com/shanglianlm0525/CvPytorch Py…...
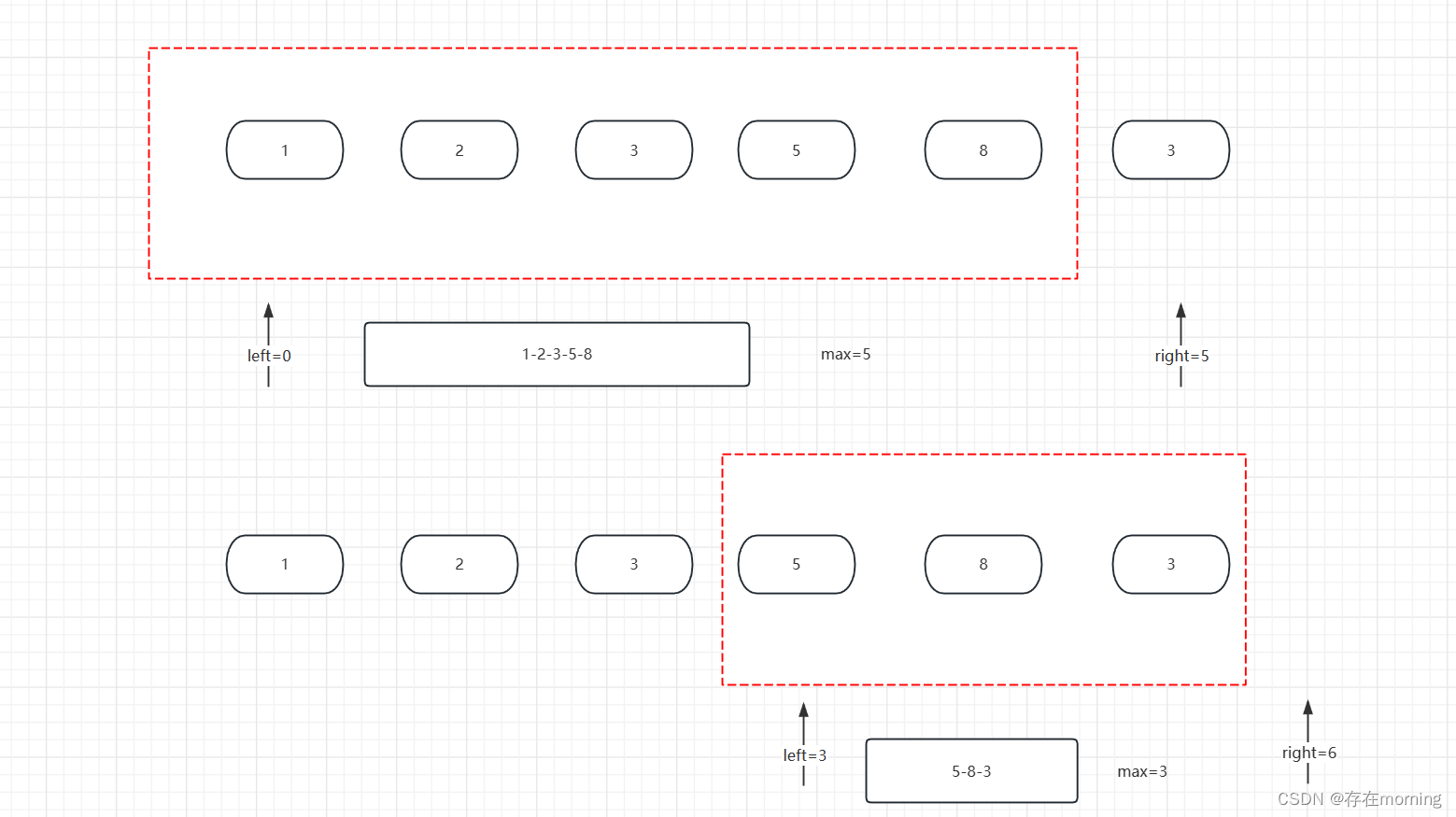
【算法训练-字符串】一 最长无重复子串
废话不多说,喊一句号子鼓励自己:程序员永不失业,程序员走向架构!本篇Blog的主题是最长无重复子串或最长无重复子数组,这类题目出现频率还是很高的。 最长无重复子串【MID】 先来看字符串数据结构的题目 题干 解题思…...
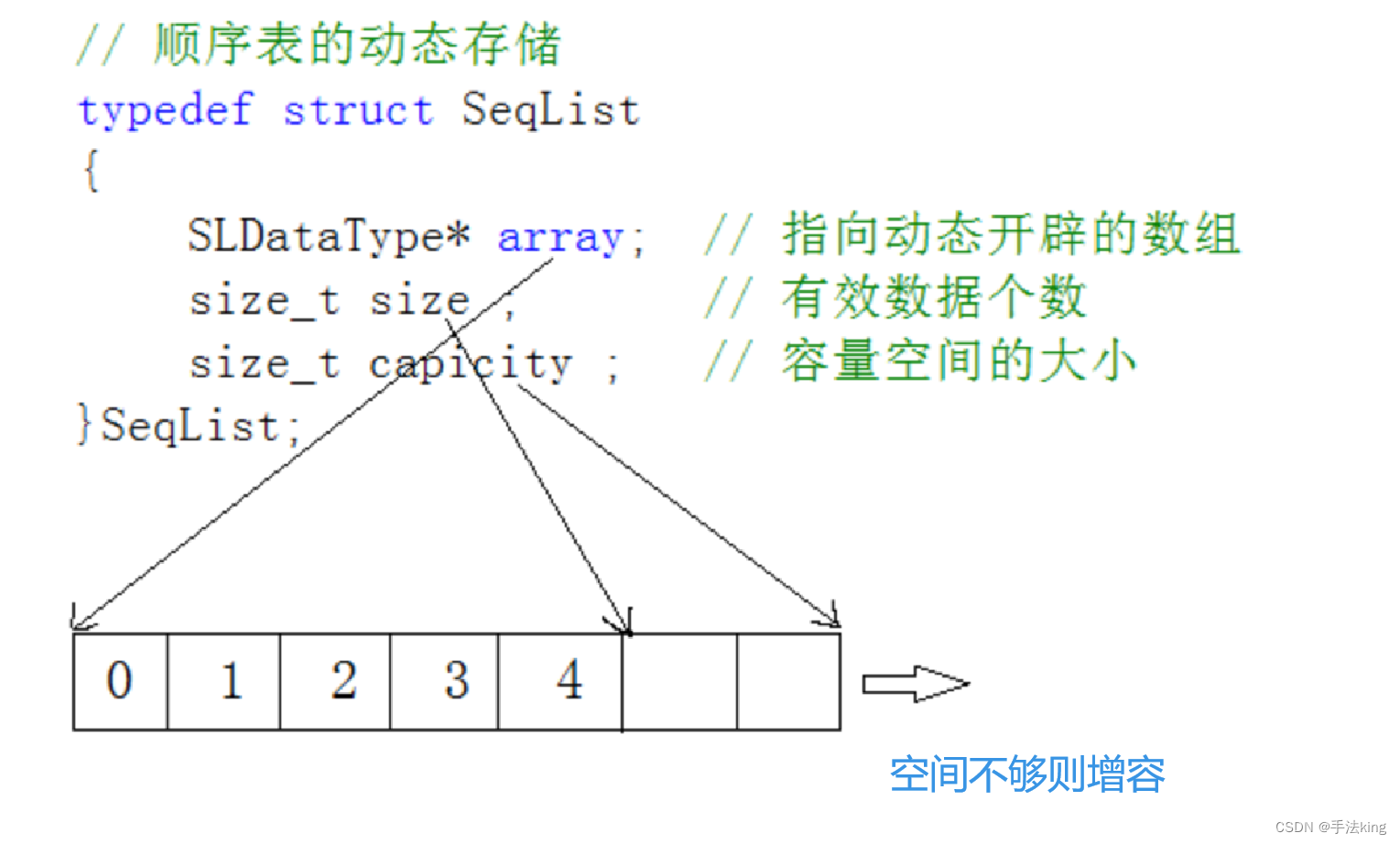
【数据结构】手撕顺序表
一,概念及结构 顺序表是用一段物理地址连续的存储单元依次存储数据元素的线性结构,一般情况下采用数组存储; 在数组上完成数据的增删查改。 1, 静态顺序表:使用定长数组存储元素。 2.,动态顺序表࿱…...
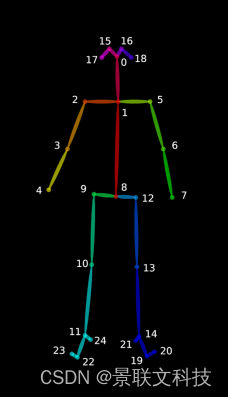
景联文科技数据标注:人体关键点标注用途及各点的位置定义
人体关键点标注是一种计算机视觉任务,指通过人工的方式,在指定位置标注上关键点,例如人脸特征点、人体骨骼连接点等,常用来训练面部识别模型以及统计模型。这些关键点可以表示图像的各个方面,例如角、边或特定特征。在…...

typescript基础之never
TypeScript 的 never 类型是一种特殊的类型,它表示的是那些永远不存在的值的类型。例如,一个抛出异常或无限循环的函数的返回值类型就是 never,因为它们永远不会返回任何值。never 类型是所有类型的子类型,也就是说,任…...

电子电路学习笔记之NCP304LSQ37T1G ——超低电流电压检测器
超低电流电压检测器是一种专门用于检测极小电流值的设备。它们常用于电子元件或电路中,用于监测电流的存在和程度。这些检测器通常具有高灵敏度和高精度,能够测量微安级别或更小的电流。 超低电流电压检测器的应用领域广泛,例如电池管理系统…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

智能职业发展系统:AI驱动的职业规划平台技术解析
智能职业发展系统:AI驱动的职业规划平台技术解析 引言:数字时代的职业革命 在当今瞬息万变的就业市场中,传统的职业规划方法已无法满足个人和企业的需求。据统计,全球每年有超过2亿人面临职业转型困境,而企业也因此遭…...

OpenGL-什么是软OpenGL/软渲染/软光栅?
软OpenGL(Software OpenGL)或者软渲染指完全通过CPU模拟实现的OpenGL渲染方式(包括几何处理、光栅化、着色等),不依赖GPU硬件加速。这种模式通常性能较低,但兼容性极强,常用于不支持硬件加速…...
