C#,数值计算——Midexp的计算方法与源程序

1 文本格式
using System;
namespace Legalsoft.Truffer
{
public class Midexp : Midpnt
{
public new double func(double x)
{
return funk.funk(-Math.Log(x)) / x;
}
public Midexp(UniVarRealValueFun funcc, double aa, double bb) : base(funcc, aa, bb)
{
base.a = 0.0;
base.b = Math.Exp(-aa);
}
}
}
2 代码格式
using System;namespace Legalsoft.Truffer
{public class Midexp : Midpnt{public new double func(double x){return funk.funk(-Math.Log(x)) / x;}public Midexp(UniVarRealValueFun funcc, double aa, double bb) : base(funcc, aa, bb){base.a = 0.0;base.b = Math.Exp(-aa);}}
}相关文章:

C#,数值计算——Midexp的计算方法与源程序
1 文本格式 using System; namespace Legalsoft.Truffer { public class Midexp : Midpnt { public new double func(double x) { return funk.funk(-Math.Log(x)) / x; } public Midexp(UniVarRealValueFun funcc, double aa, d…...
和wx.getStorageSync())
微信小程序使用本地存储方法wx.setStorageSync()和wx.getStorageSync()
微信小程序的本地存储可以使用wx.setStorageSync()和wx.getStorageSync()方法实现 使用wx.setStorageSync()方法可以将数据以键值对的方式存储到本地存储中: wx.setStorageSync(demo, demo123);获取数据:使用wx.getStorageSync()方法可以从本地存储中获…...

题解:ABC317C - Remembering the Days
题解:ABC317C - Remembering the Days 题目 链接:Atcoder。 链接:洛谷。 难度 算法难度:B。 思维难度:B。 调码难度:C。 综合评价:普及-。 算法 深度优先搜索。 思路 先建图&#x…...

【CSS】简记CSS效果:通过transition(动画过渡属性)实现侧边栏目滑入滑出
需求 在资金明细的页面中,点击按钮时筛选区域从左侧滑出,完成筛选点击确认后调用接口完成数据查询,筛选区域滑入左侧; 基于微信小程序页面实现 wxml代码 <view><!-- 操作按钮 --><button type"primary&qu…...
)
LeetCode——最大子数组和(中等)
题目 给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。 子数组 是数组中的一个连续部分。 示例 1: 输入:nums [-2,1,-3,4,-1,2,1,-5,4] 输出&#x…...

Zookeeper集成SpringBoot
Curator 是 Apache ZooKeeper 的Java客户端库。 Zookeeper现有常见的Java API如:原生JavaAPI、Curator、ZkClient等。 pom.xml <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0"…...
ModaHub魔搭社区:星环科技致力于打造更优越的向量数据库
在数字化时代,数据成为了最重要的资源之一。随着人工智能、大数据等技术的不断发展,向量数据库成为了处理这类数据的关键工具。星环科技作为一家专注于数据存储和管理技术的公司,其重要目标就是将向量数据库打造得更为优越。 在星环科技,有一个专注于向量数据库的团队。这个…...

Dubbo默认使用什么序列化框架?还有哪些?
Dubbo默认使用的序列化框架是Hessian 2.0。Hessian是一种基于二进制的序列化协议,它具有简单、高效的特点,适用于网络传输和存储数据。Hessian在Dubbo中被广泛使用,因为它可以在不同的编程语言之间进行对象的序列化和反序列化。 除了Hessian…...

攻防世界-What-is-this
原题 解题思路 解压后文件 没有后缀,不知道是什么文件。用notepad打开找不到flag。 尝试当成压缩包解压。 用stegsolve以打开图片1, 合成两张图片。...

[C++]构造与毁灭:深入探讨C++中四种构造函数与析构函数
个人主页:北海 🎐CSDN新晋作者 🎉欢迎 👍点赞✍评论⭐收藏✨收录专栏:C/C🤝希望作者的文章能对你有所帮助,有不足的地方请在评论区留言指正,大家一起学习交流!ǹ…...

【跟小嘉学 Rust 编程】二十一、网络编程
系列文章目录 【跟小嘉学 Rust 编程】一、Rust 编程基础 【跟小嘉学 Rust 编程】二、Rust 包管理工具使用 【跟小嘉学 Rust 编程】三、Rust 的基本程序概念 【跟小嘉学 Rust 编程】四、理解 Rust 的所有权概念 【跟小嘉学 Rust 编程】五、使用结构体关联结构化数据 【跟小嘉学…...
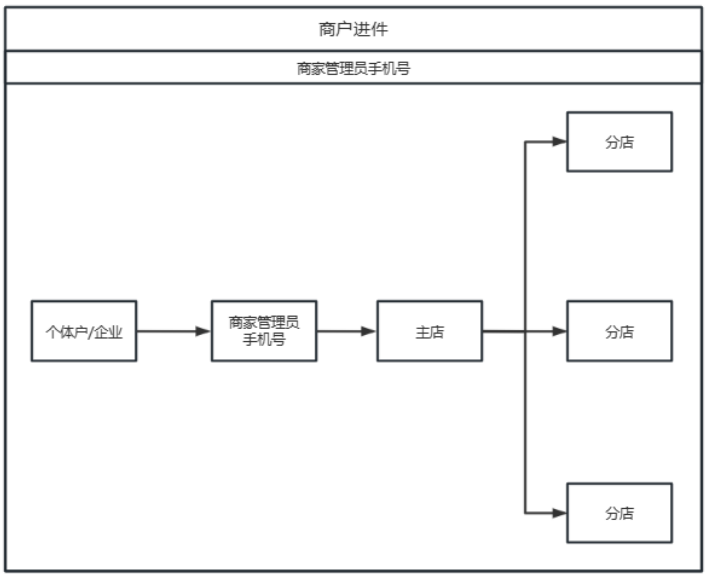
一文了解聚合支付
第四方支付是相对于第三方支付而提出的概念,又被称为“聚合支付”是指通过聚合第三方支付平台、合作银行、等多种支付工具进行的综合支付服务。 简言而之,把支付接口聚合到一个平台上面,来给商家或者个人来提供支付服务。 第四方支付集中了各…...
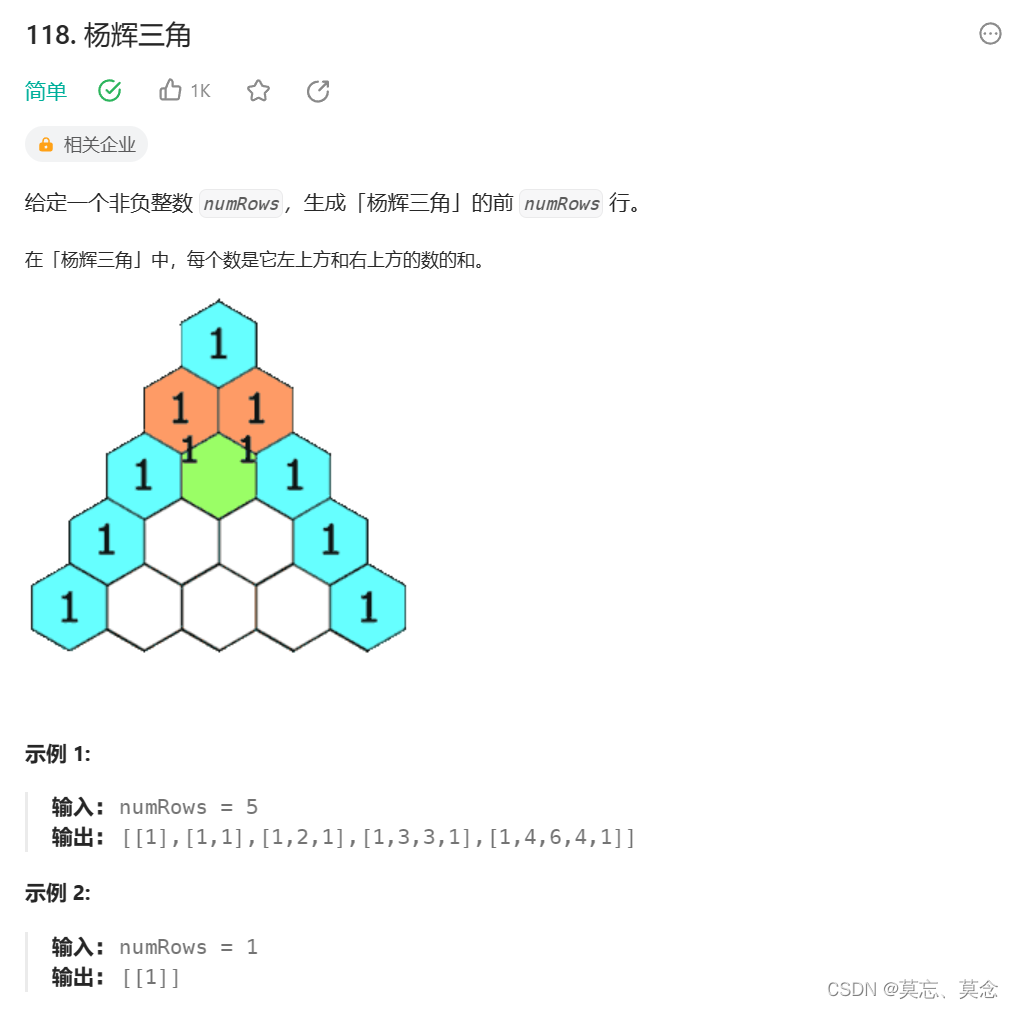
118.杨辉三角
一、题目 118. 杨辉三角 - 力扣(LeetCode) 二、代码 class Solution { public:vector<vector<int>> generate(int numRows) {vector<vector<int>>data(numRows);for(int i0;i<numRows;i){data[i].resize(i1);//扩容data[i]…...
第7节——渲染列表+Key作用
一、列表渲染 我们再react中如果渲染列表,一般使用map方法进行渲染 import React from "react";export default class LearnJSX2 extends React.Component {state {infos: [{name: "张三",age: 18,},{name: "李四",age: 20,},{nam…...

NTP服务器时间配置
简介 ntp服务器是一个同步时间都服务器。 开启ntpd 1.查看状态(可以看到状态为:inactive,也就是没有启动ntp服务) [rootlocalhost]$ systemctl status ntpd ● ntpd.service - Network Time ServiceLoaded: loaded (/usr/lib/…...
vulhub之MinIO信息泄露漏洞(CVE-2023-28432)
文章目录 0x01 前言0x02 漏洞描述0x03 影响范围0x04 漏洞复现1.启动环境2.查看端口3.构造POC 0x05 修复建议 0x01 前言 本次测试仅供学习使用,如若非法他用,与本文作者无关,需自行负责!!! 0x02 漏洞描述 …...

C语言:递归思想及实例详解
简介:在计算机科学中是指一种通过重复将问题分解为同类的子问题而解决问题的方法。通过函数的自调用化繁为简。 递归可以说是编程中最神奇的一种算法。因为我们有时候可能不能完全明晰代码的运行过程,但是我们却知道代码可以跑出正确的结果。而当我们使…...

好题分享0
P2141 [NOIP2014 普及组] 珠心算测验 原题链接 : [NOIP2014 普及组] 珠心算测验 - 洛谷 思路 : 用哈希表来存出现过的两数之和,最后ans即可 代码 : #include<bits/stdc.h> #define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0); #define end…...
python的asyncio事件循环
一、介绍 asyncio是Python标准库中的一个异步编程框架,它提供了一个事件循环(event loop),用于协调异步任务的执行和结果的返回。在asyncio中,事件循环是一个非常重要的概念,它是异步编程的核心。 事件循…...

QT day1登录界面设计
要设计如下图片: 代码如下: main.cpp widget.h widget.cpp 运行效果: 2,思维导图...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...
