C语言:递归思想及实例详解
简介:在计算机科学中是指一种通过重复将问题分解为同类的子问题而解决问题的方法。通过函数的自调用化繁为简。
递归可以说是编程中最神奇的一种算法。因为我们有时候可能不能完全明晰代码的运行过程,但是我们却知道代码可以跑出正确的结果。而当我们使用其他算法,我们必须将代码运行的每一个细节都弄清楚才能确保代码的正确性。这就是递归的神奇之处。
下面由浅入深对递归进行解析:
1.阶乘计算
相信这是每个人初学递归时都会遇到的问题。当然这也是最容易理解的一种递归,思路很简单:
如果要计算n的阶乘,我们可以先算出n-1的阶乘再乘上n,如果要计算n-1的阶乘,我们可以先算出n-2的阶乘再乘上n-1,依此类推,递归逐渐深入,我们只需要给出1的阶乘和0的阶乘,然后递归就会不断返回,最后算出n的阶乘。
这一点还是比较容易理解,此处不作赘述。
int f(int n)
{if (n == 0 || n == 1)return 1;elsereturn n * f(n - 1);
}2.爬楼梯
爬楼梯OJ
题目概述:
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
这也是一个典型可以用递归解决的问题
思路:如果我们要到达n阶,我们可以从n-1阶往上跳一个台阶,或者从n-2阶往上跳2个台阶,我们可以想想是不是只有这两种情况?所以到达n阶的方法数量是不是就是到达n-1阶的方法数量和到达n-2阶的方法数量之和?答案是显然的。那么这个问题是不是就和第一个例题类似了,只是这里的递归分支了,但是本质上是相同的,我们只需要给出到达1阶和到达2阶的方法数量,递归就能返回到n阶的方法数量。
int climbStairs(int n){if(n==1)return 1;else if(n==2)return 2;elsereturn climbStairs(n-1)+climbStairs(n-2);
}需要注意的是:这里给出的代码并不能通过,因为分支递归在递归层数过深的时候很容易超时,举个例子,我们要计算到达10阶的方法数,我们要算9阶和8阶.......
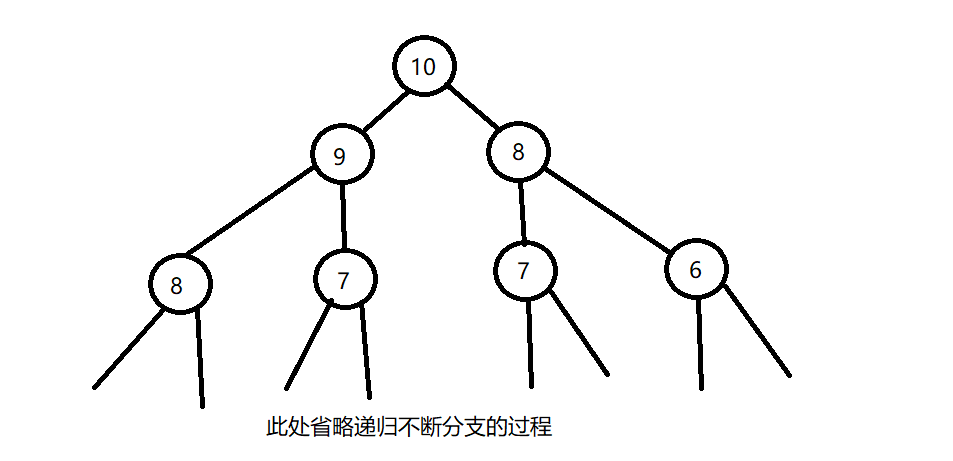
这里递归的时间复杂度是O(2^n),n过大时超时是必然的。如果要避免超时可以使用迭代(循环)代替递归。使用递归的优势是代码逻辑更加明了,而迭代的优势是速度更快,如果递归分支了那么迭代的优势会更加明显。
这里给出迭代的方法仅供参考,不作讨论
int climbStairs(int n){if(n==1)return 1;if(n==2)return 2;int a=1;int b=2;int c;while(n>=3){c=a+b;a=b;b=c;n--;}return c;
}3.找最大值
要求很简单,写一个函数
int find(int*nums,int numsSize)要求返回nums数组的最大值。最简单的方法是定义一个max变量遍历nums并更新max最后返回即可。如果使用递归该怎么做呢?
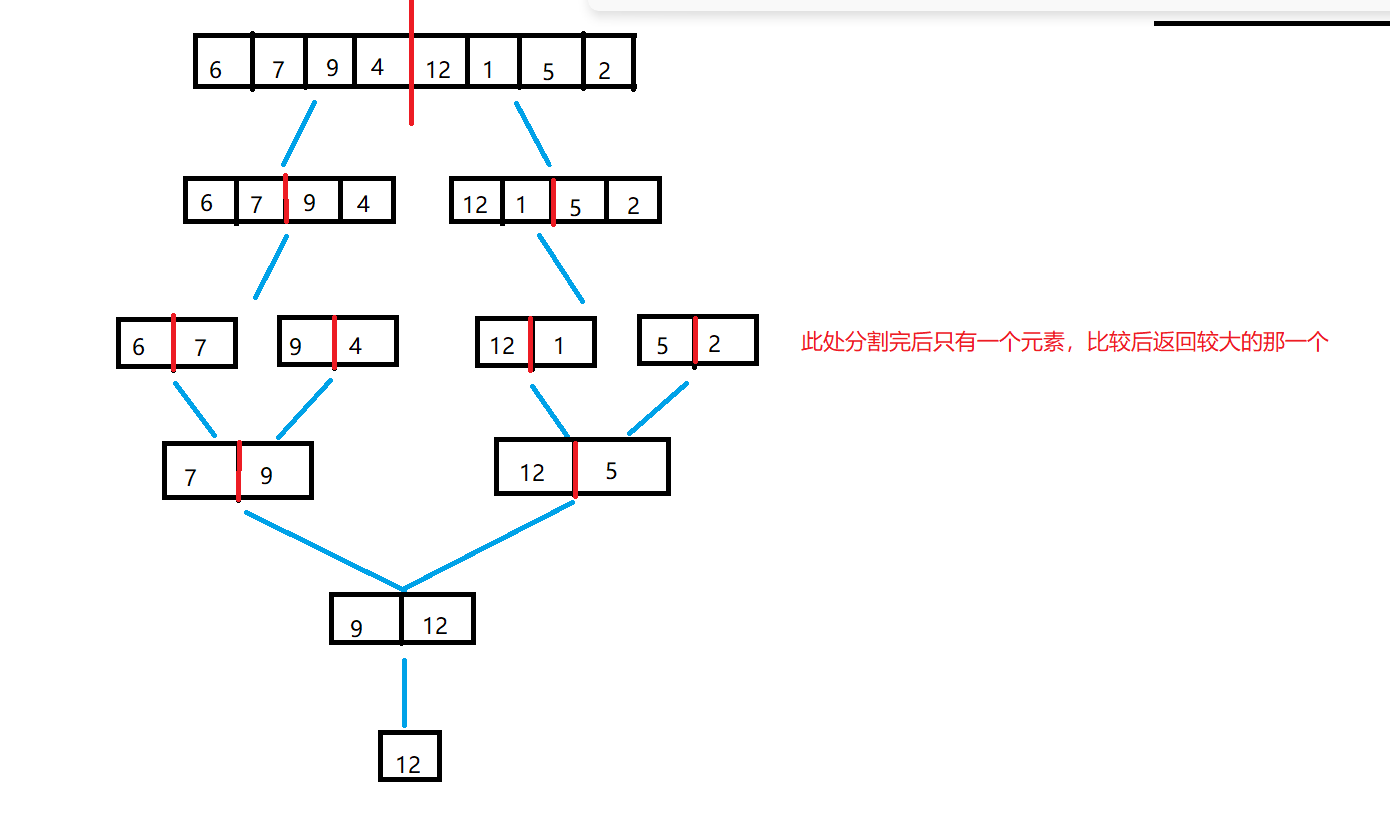
思路:我们将nums平分为左右两个部分,记左半部分最大值为max1,右半部分最大值为max2,那么显然整个nums的最大值是max1和max2中较大的一个。那么同样的,max1和max2是如何得到的呢?我们将左右部分分别再次平分........不断进行下去,知道最后平分完之后一个元素单独组成一个部分,那么这个部分的最大值就是这个单独的元素
int max(int* nums, int numsSize)
{int right = numsSize - 1;if (right == 0)return nums[0];else{int mid = right / 2;return max(nums, mid + 1) > max(nums + mid + 1, right -mid)? max(nums, mid + 1): max(nums + mid + 1, right - mid);}
}以下是一个示意图:
教学视频:
在这里强烈推荐一个视频,视频链接,看完这个视频会对递归以及接下来的问题有更深刻的认识
4.归并排序
从这个部分开始递归就上了一个档次,第三个问题其实是这个问题的铺垫
归并排序的原理:与第三个问题一样,将数组细分直到每个部分只有一个元素,此时每个部分可以看作升序,使用merge函数将两部分合并成一个升序的部分(merge函数是将[4,8,9,10,1,2,3]这样两个部分为升序的数组排成完全升序的数组,力扣上有类似的实现merge函数的OJ 合并两个有序数组,但是这里是仅处理一个数组,只需要进行一些细节处理就能转换成相同问题)
归并排序的实现
void sort(int* arr1, int left, int right)
{if (right == left)return;int mid = left + (right - left) / 2;//将左半部分排序sort(arr1, left, mid);//将右半部分排序sort(arr1, mid + 1, right);//将两个升序部分排成完全升序merge(arr1, left, mid, right);
}merge的实现
void merge(int* arr, int start, int mid, int end)
{int* copy = (int*)malloc(sizeof(int) * (end -start+ 1));memcpy(copy, arr+start,(end-start+1)*sizeof(int));int count = start;int count1 = 0;int count2 = mid-start+1;while (count1 <= mid-start && count2 <= end-start){if (copy[count1] <= copy[count2]){arr[count++] = copy[count1++];}else{arr[count++] = copy[count2++];}}if(count1==mid-start+1){while (count2 <= end-start){arr[count++] = copy[count2++];}}else{while (count1 <= mid-start){arr[count++] = copy[count1++];}}free(copy);
}在上边给出的教学视频里包含详细的动画展示,这里就不画图进行模拟了。
5.汉诺塔问题

有A、B、C三根柱子,初始状态A柱子上有若干个盘子,目标是将A上的所有盘子移动到C柱子上,并且小盘子在上,大盘子在下,与初始状态相同。移动过程中大盘子不能放在小盘子上。
我们设计一个函数
void hano(int n,char a,char b,char c)很多人对函数的四个参数不理解,或者理解不深刻,包括一些博文对几个参数都没有很好的解释。在这里先进行一个简单的分析,在后面的代码中会深入剖析。
参数分析:
很明显n表示A柱子上有n个盘子,奇怪的是为什么要三个char类型变量???其实很简单,这里的三个char类型形参接收的分别常量'A' 'B' 'C'中的一个。这个函数的含义是:将a变量的柱子上的n-1个盘子移动到b变量的盘子上,再将a变量柱子上第n个(最大的)盘子移动到c变量柱子上,最后将b变量柱子上的n-1个盘子移动到c变量柱子上。举个例子:
hano(15,'B','A','C');表示将B柱子上的14个盘子移动到A,再把B上最后一个盘子移动到C上,再把A上n-1个盘子移动到C上
但是n-1个盘子是不能直接移动的,所以具体是怎么移动的呢?
当n=2时,我们会使用这个函数
hano(2,'A','B','C');这样n-1=1,我们每次只会移动一个盘子,就可以直接移动了。
当n=3时,我们需要把2个盘子从A移动到B上,于是我们使用
hano(n-1,'A','C','B');那么怎么把2个盘子移动到B上?我们首先要把1个盘子移动到C上
那么对于n个盘子,我们的思路也一样
//move中的n表示的是 第n个盘子
void move(int n, char soure, char destination)
{printf("move %d from %c to %c\n", n, soure, destination);
}
void hano(int n,char a,char b,char c)
{if (n == 1){move(1, a, c);}else{//将n-1个盘子从a移动到b上//问题:既然是从a到b,那么和第二个参数有什么关系呢?为什么需要第二个参数?hano(n - 1, a, c, b);move(n, a, c);//只有一个盘子了,直接打印出移动轨迹hano(n - 1, b, a, c);}
}现在对代码中提出的问题进行解答:我们再hano函数中再次调用hano,三个参数的值是会来回hano知道这一步的三hano才能推测下一步的三个参数,少一个参数hano函数就不能正常递归了
到了这里文章就结束了,最后再次推荐大家看一看文章给出的视频,看完会对递归有更深刻的认识。
相关文章:

C语言:递归思想及实例详解
简介:在计算机科学中是指一种通过重复将问题分解为同类的子问题而解决问题的方法。通过函数的自调用化繁为简。 递归可以说是编程中最神奇的一种算法。因为我们有时候可能不能完全明晰代码的运行过程,但是我们却知道代码可以跑出正确的结果。而当我们使…...

好题分享0
P2141 [NOIP2014 普及组] 珠心算测验 原题链接 : [NOIP2014 普及组] 珠心算测验 - 洛谷 思路 : 用哈希表来存出现过的两数之和,最后ans即可 代码 : #include<bits/stdc.h> #define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0); #define end…...
python的asyncio事件循环
一、介绍 asyncio是Python标准库中的一个异步编程框架,它提供了一个事件循环(event loop),用于协调异步任务的执行和结果的返回。在asyncio中,事件循环是一个非常重要的概念,它是异步编程的核心。 事件循…...

QT day1登录界面设计
要设计如下图片: 代码如下: main.cpp widget.h widget.cpp 运行效果: 2,思维导图...
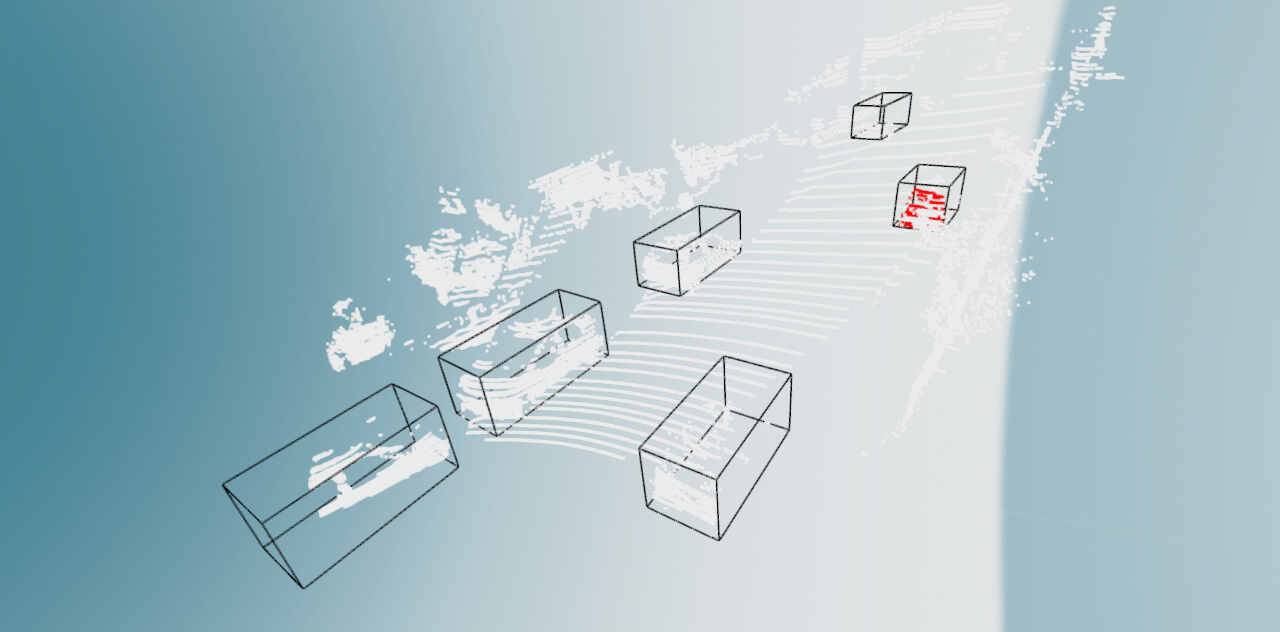
(一)KITTI数据集用于3D目标检测
KITTI数据集介绍 数据基本情况 KITTI是德国卡尔斯鲁厄科技学院和丰田芝加哥研究院开源的数据集,最早发布于2012年03月20号。 对应的论文Are we ready for Autonomous Driving? The KITTI Vision Benchmark Suite发表在CVPR2012上。 KITTI数据集搜集自德国卡尔斯鲁厄市&…...

手写Promise完整介绍
Promise是一种用于处理异步操作的机制,它可以将异步操作的结果以同步的方式进行处理和返回。在JavaScript中,Promise是一种内置对象,但我们也可以手动实现一个Promise类来更好地理解其原理和工作方式。 Promise的特性 首先,让我…...
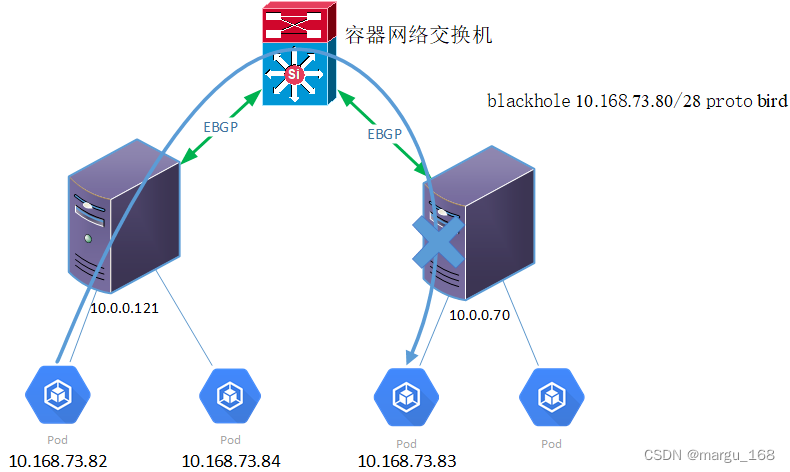
【kubernetes系列】Calico原理及配置
概述 Calico是针对容器,虚拟机和基于主机的本机工作负载的开源网络和网络安全解决方案。 Calico支持广泛的平台,包括Kubernetes,OpenShift,Docker EE,OpenStack和裸机服务。 Calico在每个计算节点都利用Linux Kernel实…...
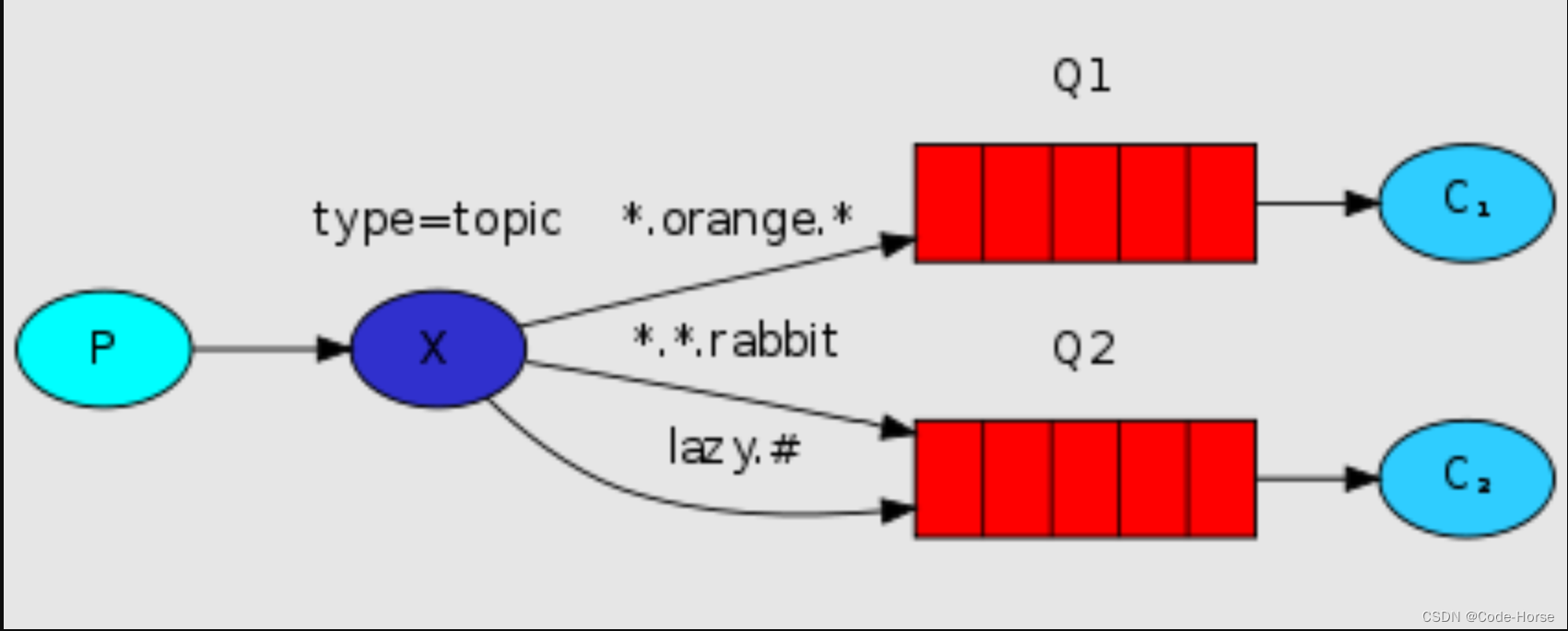
RabbitMQ 的快速使用
docker部署rabbitmq # management才有管理页面 docker pull rabbitmq:management# 新建容器并运行 docker run \-e RABBITMQ_DEFAULT_USERadmin \ -e RABBITMQ_DEFAULT_PASSadmin \ -v mq-plugins:/plugins \--name mq \--hostname mq \-p 15672:15672 \-p 5672:5672 \-itd \ra…...

VUE3添加全局变量
全局变量的添加 在vue3.0中注入全局方法不是在prototype上挂载了,而是添加在config.globalProperties属性上。 //main.js import { createApp } from "vue"; import App from "./App.vue";const app createApp(App); app.config.globalPrope…...
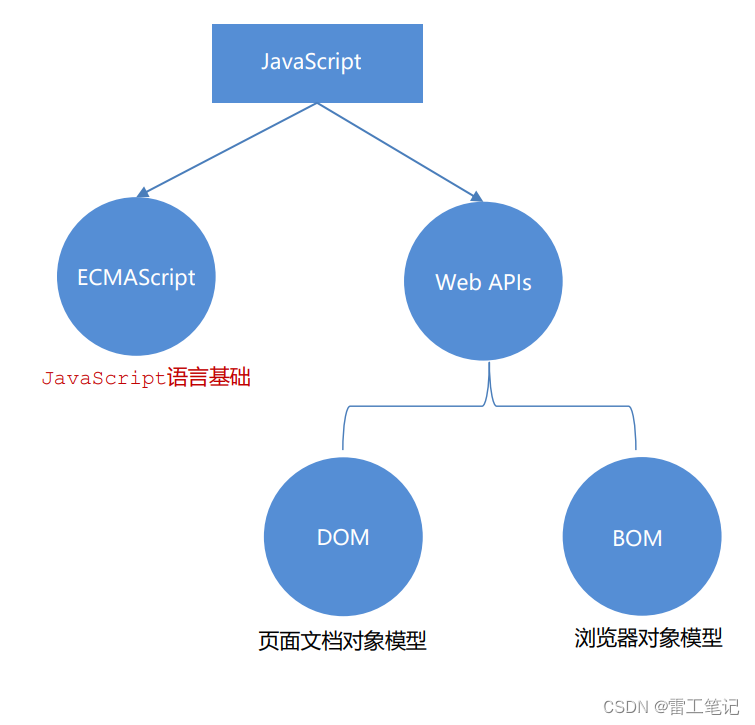
JavaScript基础语法01——初识JavaScript
哈喽,大家好,我是雷工! 最近有项目用到KingFusion软件,由于KingFusion是B/S架构的客户端组态软件,因此在学习KingFusion产品时会涉及许多前端的知识。 像JavaScript语言就是需要用的,俗话说:活到…...
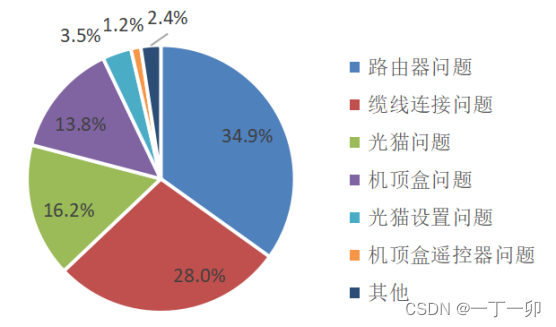
家宽用户家庭网的主要质量问题是什么?原因有哪些
1 引言 截至2020年底,我国家庭宽带(以下简称“家宽”)普及率已达到96%。经过一年多的发展,当前,家庭宽带的市场空间已经饱和。运营商在家宽市场的竞争也随之从新增用户数的竞争转移到家宽品质的竞争。 早期运营商的家…...
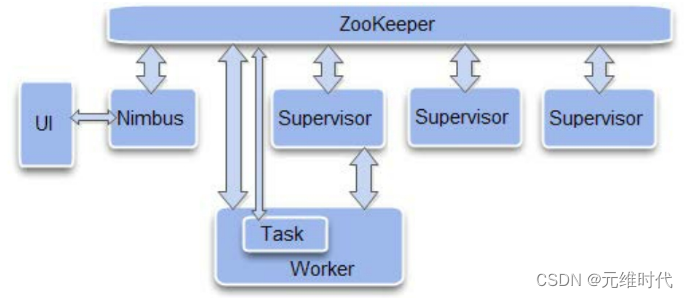
ZooKeeper的典型应用场景及实现
文章目录 1、典型应用场景及实现1.1、 数据发布/订阅1.1.1、配置管理案列 1.2、负载均衡1.3、命名服务1.4、分布式协调/通知1.4.1、一种通用的分布式系统机器间通信方式 1.5、集群管理1.6、Master选举1.7、分布式锁1.7.1、排他锁1.7.2、共享锁 1.8、分布式队列 2、ZooKeeper在大…...

智能安全帽~生命体征检测与危险气体检测一体化集成设计还是蓝牙无线外挂式方式好?
生命体征(心率、血氧等)检测&上报平台,危险气体采集&上报平台,是智能安全帽产品中常见的两种选配件,它们的实现有两种典型的模式: 1)将传感器集成到主板上,做成一体化的智能…...

【Java并发】聊聊对象内存布局和syn锁升级过程
对象存储解析:一个空Object对象到底占据多少内存? 对象内存布局 Mark Word占用8字节,类型指针占用8个字节,对象头占用16个字节。 好了,我们来看一下一个Object对占用多少空间, 因为java默认是开启压缩…...

【档案专题】八、电子档案鉴定与销毁
导读:主要针对电子档案鉴定与销毁相关内容介绍。对从事电子档案管理信息化的职业而言,不断夯实电子档案管理相关理论基础是十分重要。只有通过不断梳理相关知识体系和在实际工作当中应用实践,才能走出一条专业化加职业化的道路,从…...

进程与子进程
一、子进程 1.fork()创建子进程 一个现有的进程可以调用 fork()函数创建一个新的进程,调用 fork()函数的进程称为父进程,由 fork()函数创建出来的进程被称为子进程(child process)。(使用该函数需要包含头文件<uni…...

如何对MySQL和MariaDB中的查询和表进行优化-提升查询效率
前言 MySQL和MariaDB是数据库管理系统的流行选择。两者都使用SQL查询语言来输入和查询数据。 尽管SQL查询是简单易学的命令,但并不是所有的查询和数据库函数都具有相同的效率。随着你存储的信息量的增长,如果你的数据库支持一个网站,随着网…...

【Android】关于binder_calls_stats服务
Android 9上有了binder_calls_stats服务,提供了java层的binder统计, Android中的Binder Call Stats(Binder调用统计)是一项用于监控和记录Android系统中Binder通信的统计信息的功能。Binder是Android中的一种进程间通信ÿ…...

给前端返回http链接,由于浏览器缓存不能获取到最新资源怎么办?
1、问题描述 今天在工作中接到这样一个需求,接收前端的图片文件并上传到远程,将原有图片覆盖并返回一个http链接以供前端展示。用户使用后反馈没有修改成功,上了远程拉图片发现已经修改了,但是用户浏览器还是老的图片。排查原因是…...

【Java Web】检查用户登录状态,防止用户访问到非法页面
使用拦截器 在方法前标注自定义注解拦截所有请求,只处理带有该注解的方法 自定义注解: 常用元注解:Target, Rentention, Document, Inherited如何读取注解: - Method.getDeclaredAnnotations() - Method.getAnnotaion(Class<T&…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...
