HuggingFace中的 Files and versions 如何优雅下载到本地?(Python requests,tqdm)
前言
在使用huggingface把玩各种大模型时,如果选择从远程加载模型,这个过程可能因为网络问题而非常耗时甚至直接失败,所以把模型、分词器等相关文件下载到本地,再直接从本地加载就成了不可回避的流程。
在进入具体版本的模型后,我们可以去Files and Versions这个菜单项下面找到需要下载到本地的全部模型(以WizardCoder为例)
第一步是获取我们想要下载的文件的下载时url
在文件大小的右侧,可以看到一个向下的箭头表示下载,鼠标移动到箭头上,右键,选择“复制链接地址”,这样就得到了下载时url
我们将这些url存放到list中。
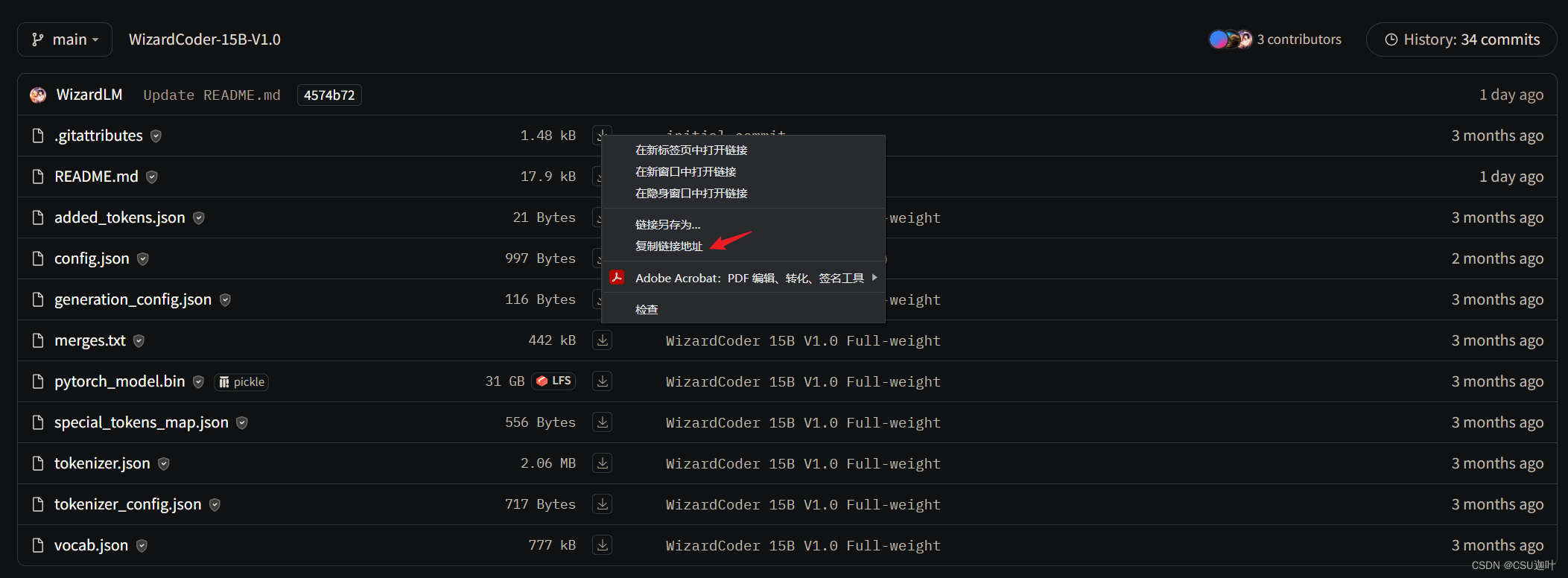
第二步就是python代码,这里除了用于请求的request库,我还使用了tqdm库,tqdm也可通过pip install来安装,它的作用是在下载较大的文件时,我们可以在终端看到下载的速度和进度
import requests
import os
from tqdm import tqdmurls = ["https://huggingface.co/WizardLM/WizardCoder-15B-V1.0/resolve/main/pytorch_model.bin"
]filepath = "WizardCoder/WizardCoder-15B-V1.0"def download_file(url):filename = url.split("/")[-1]download_path = os.path.join(filepath, filename)response = requests.get(url, stream=True, verify=False)response.raise_for_status()file_size = int(response.headers.get("Content-Length", 0)) # 获取待下载的文件大小chunk_size = 8192 # 读取的数据块的大小是8千字节with open(download_path, "wb") as file, tqdm(total=file_size, unit="B", unit_scale=True, unit_divisor=1024, desc=filename) as progress_bar:for chunk in response.iter_content(chunk_size=chunk_size):if chunk:file.write(chunk)progress_bar.update(1)for url in urls:download_file(url)
相关文章:

HuggingFace中的 Files and versions 如何优雅下载到本地?(Python requests,tqdm)
前言 在使用huggingface把玩各种大模型时,如果选择从远程加载模型,这个过程可能因为网络问题而非常耗时甚至直接失败,所以把模型、分词器等相关文件下载到本地,再直接从本地加载就成了不可回避的流程。 在进入具体版本的模型后&…...
三、原型模式
一、什么是原型模式 原型(Prototype)模式的定义如下:用一个已经创建的实例作为原型,通过复制该原型对象来创建一个和原型相同或相似的新对象。在这里,原型实例指定了要创建的对象的种类。用这种方式创建对象非常高效&a…...

transformer实现词性标注
1、self-attention 1.1、self-attention结构图 上图是 Self-Attention 的结构,在计算的时候需要用到矩阵 Q(查询), K(键值), V(值)。在实际中,Self-Attention 接收的是输入(单词的表示向量 x组成的矩阵 X) 或者上一个 Encoder block 的输出。而 Q, K, V…...

Java中异或操作和OTP算法
最近在研究加密算法,发现异或操作在加密算法中用途特别广,也特别好用。下面以Java语言为例,简单记录一下异或操作,以及在算法中的使用,包括常用的OTP算法。 一,异或操作特征 1, 相同出0&#…...
K8S最新版本集群部署(v1.28) + 容器引擎Docker部署(下)
温故知新 📚第三章 Kubernetes各组件部署📗安装kubectl(可直接跳转到安装kubeadm章节,直接全部安装了)📕下载kubectl安装包📕执行kubectl安装📕验证kubectl 📗安装kubead…...

女子垒球运动的发展·垒球1号位
女子垒球运动的发展 1. 女子垒球运动的起源和发展概述 女子垒球运动,诞生于19世纪末的美国,作为棒球运动的衍生品,经过百年的积淀,已在全球范围内广泛传播,形成了丰富的赛事文化。她的起源,可以追溯到19世…...

Debian 30 周年,生日快乐!
导读近日是 Debian 日,也是由伊恩-默多克(Ian Murdock)创立的 Debian GNU/Linux 通用操作系统和社区支持的 Debian 项目 30 周年纪念日。 不管你信不信,从已故的伊恩-默多克于 1993 年 8 月 16 日宣布成立 Debian 项目,…...
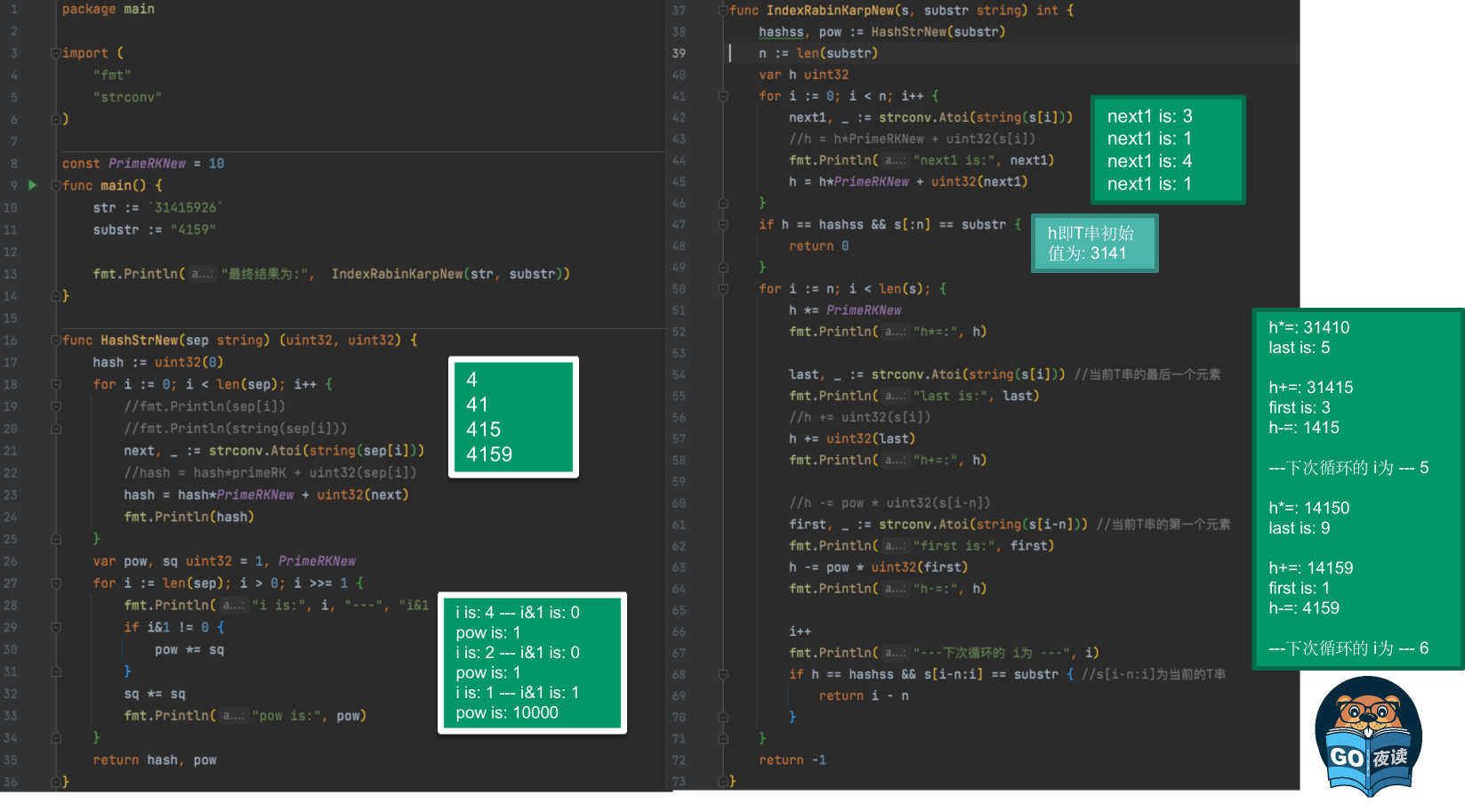
字符串匹配的Rabin–Karp算法
leetcode-28 实现strStr() 更熟悉的字符串匹配算法可能是KMP算法, 但在Golang中,使用的是Rabin–Karp算法 一般中文译作 拉宾-卡普算法,由迈克尔拉宾与理查德卡普于1987年提出 “ 要在一段文本中找出单个模式串的一个匹配,此算法具有线性时间的平均复杂度࿰…...
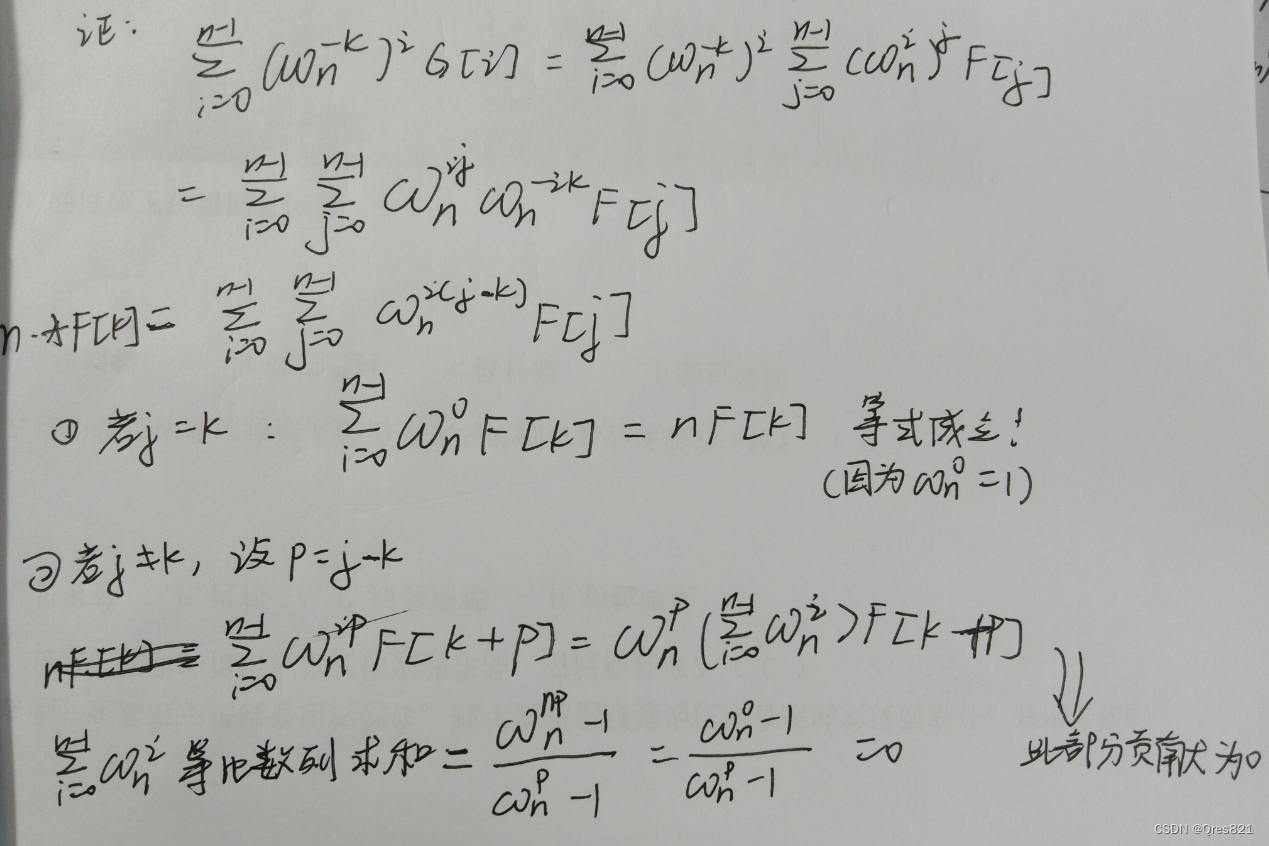
傅里叶变换(FFT)笔记存档
参考博客:https://www.luogu.com.cn/blog/command-block/fft-xue-xi-bi-ji 目录: FFT引入复数相关知识单位根及其相关性质DFT过程(难点)DFT结论(重要)IDFT结论(重要)IDFT结论证明&…...
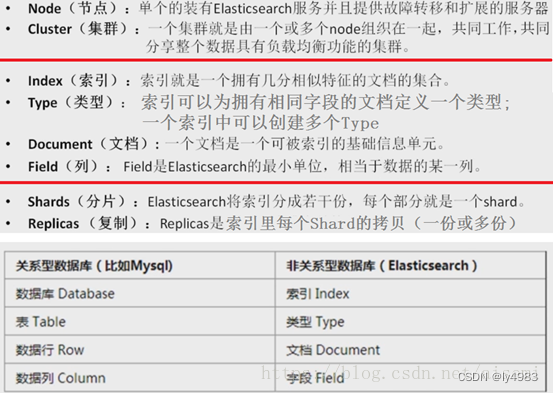
ELK安装、部署、调试 (二) ES的安装部署
ElasticSearch是一个基于Lucene的搜索服务器。它提供了一个分布式多用户能力的全文搜索引擎,基于RESTful web接口操作ES,也可以利用Java API。Elasticsearch是用Java开发的,并作为Apache许可条款下的开放源码发布,是当前流行的企业…...
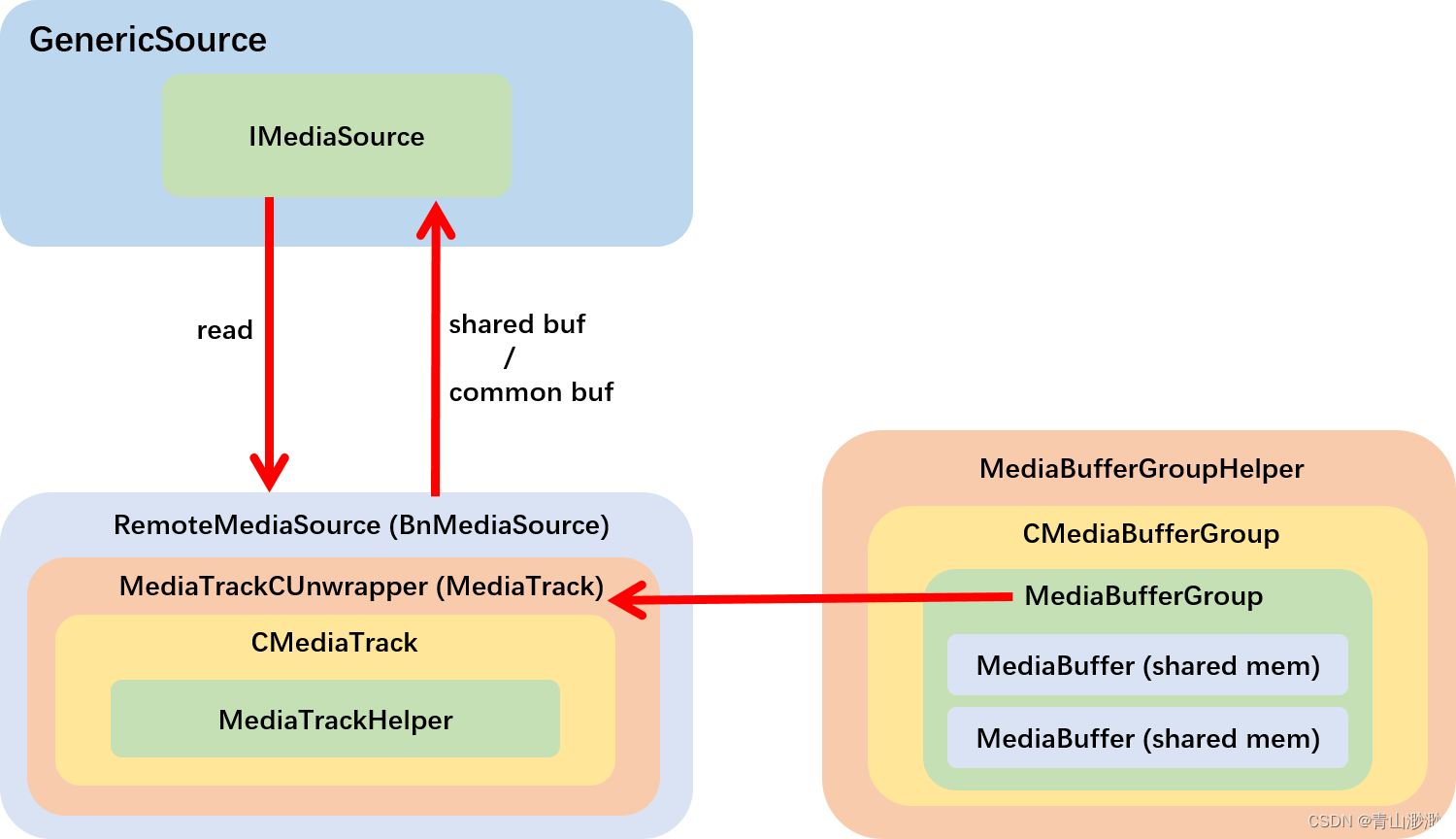
Android 13 - Media框架(8)- MediaExtractor
上一篇我们了解了 GenericSource 需要依赖 IMediaExtractor 完成 demux 工作,这一篇我们就来学习 android media 框架中的第二个服务 media.extractor,看看 IMediaExtractor 是如何创建与工作的。 1、MediaExtractorService media.extractor 和 media.p…...
Flutter 混合开发调试
针对Flutter开发的同学来说,大部分的应用还是Native Flutter的混合开发,所以每次改完Flutter代码,运行整个项目无疑是很费时间的。所以Flutter官方也给我们提供了混合调试的方案【在混合开发模式下进行调试】,这里以Android Stud…...

C语言每日一练------(Day3)
本专栏为c语言练习专栏,适合刚刚学完c语言的初学者。本专栏每天会不定时更新,通过每天练习,进一步对c语言的重难点知识进行更深入的学习。 今天练习题的关键字: 尼科彻斯定理 等差数列 💓博主csdn个人主页:…...
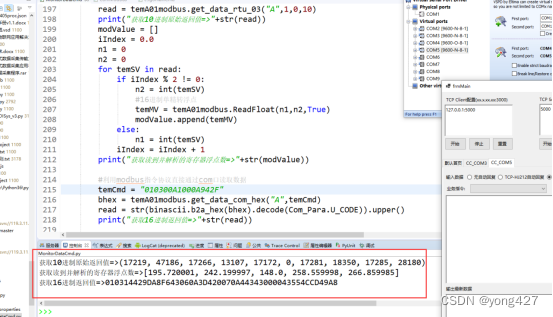
14、监测数据采集物联网应用开发步骤(10)
监测数据采集物联网应用开发步骤(9.2) Modbus rtu协议开发 本章节在《监测数据采集物联网应用开发步骤(7)》基础上实现可参考《...开发步骤(7)》调试工具,本章节代码需要调用modbus_tk组件,阅读本章节前建议baidu熟悉modbus rtu协议内容 组件安装modb…...
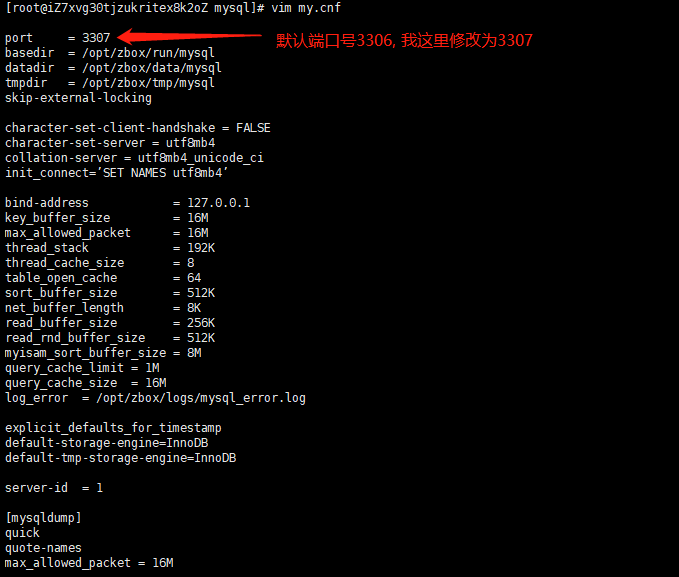
Linux禅道上修改Apache 和 MySQL 默认端口号
1. 修改Apache默认端口号 80 cd /opt/zbox/etc/apachevim httpd.conf :wq 保存 2. 修改MySQL默认端口号 3306 cd /opt/zbox/etc/mysql vim my.cnf :wq 保存 3. 重启服务 ./zbox restart...

操作教程|通过1Panel开源Linux面板快速安装DataEase
DataEase开源数据可视化分析工具(dataease.io)的在线安装是通过在服务器命令行执行Linux命令来进行的。但是在实际的安装部署过程中,很多数据分析师或者业务人员经常会因为不熟悉Linux操作系统及命令行操作方式,在安装DataEase的过…...
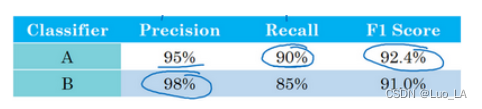
机器学习策略——优化深度学习系统
正交化(Orthogonalization) 老式电视机,有很多旋钮可以用来调整图像的各种性质,对于这些旧式电视,可能有一个旋钮用来调图像垂直方向的高度,另外有一个旋钮用来调图像宽度,也许还有一个旋钮用来…...

ES6中Proxy和Proxy实例
1.Proxy Proxy 这个词的原意是代理,用在这里表示由它来“代理”某些操作,可以译为“代理器” 使用方法 let p new Proxy(target, handler);其中,target 为被代理对象。handler 是一个对象,其声明了代理 target 的一些操作。p 是…...

UDP协议的重要知识点
UDP,即用户数据报协议(User Datagram Protocol),是一个简单的无连接的传输层协议。与TCP相比,UDP提供了更少的错误检查机制,并允许数据包在网络上更快地传输。在这篇博客中,我们将深入探讨UDP的…...
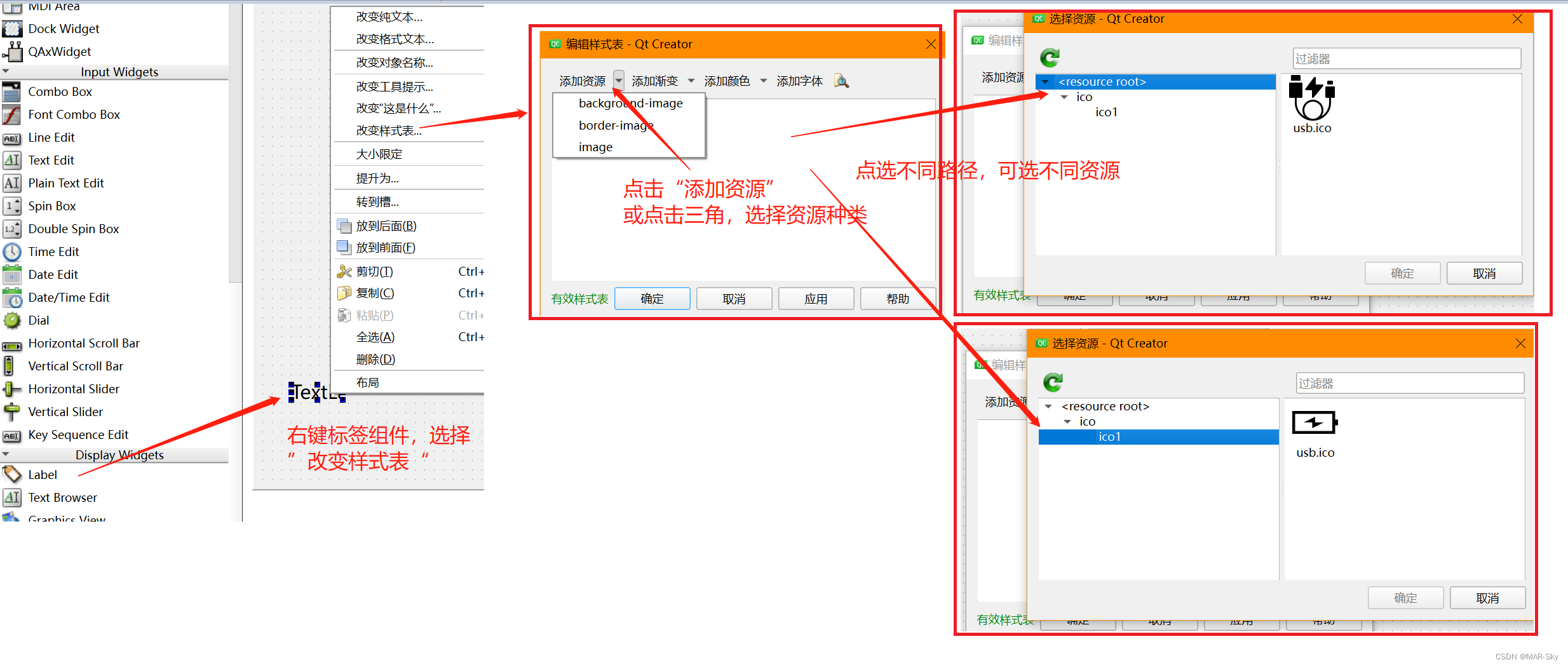
QT6为工程添加资源文件,并在ui界面引用
以添加图片资源为例 右键工程名字(不是最上面的名字),点击添加现有文件 这种方式虽然添加到了工程中,但不能在UI设计界面完成引用。主要原因可能是未把文件放入到项目资源文件中,以下面一种方式可以看出区别。 点击添…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...
