ReID网络:MGN网络(4) - Loss计算
1. MGN Loss
MGN采用三元损失(Triplet Loss)。
三元损失主要用于ReID算法,目的是帮助网络学习到一个好的Embedding信息。之所以称之为三元损失,主要原因在于在训练中,参与计算Loss的分别有Anchor、Positive和Negative三方。
2. Triplet Loss原理
Triplet Loss的任务是帮助网络训练出来一个能够准确区分不同类Embedding信息的网络。如图所示,Anchor与Positive属于同一类,与Negatine属于不同类。我们的目的就是学习一个网络,该网络能够将Anchor与Positive的距离拉近,同时将与Negative的距离推远。
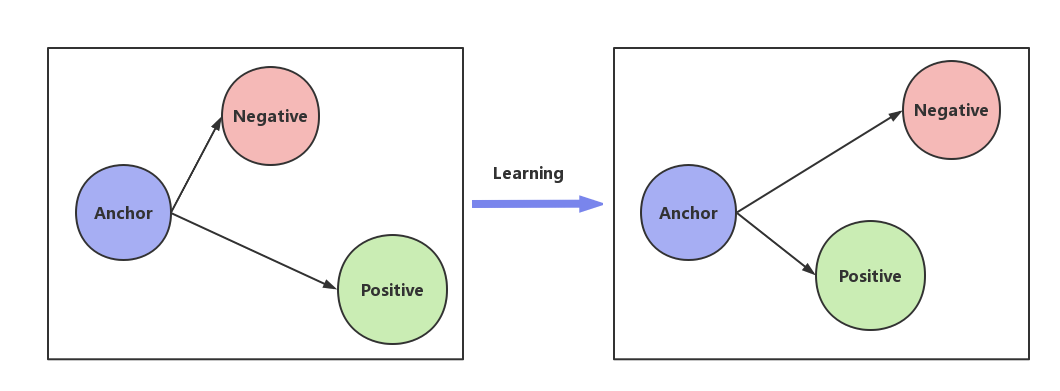
记Anchor与Positive的距离为d(a, p),Anchor与Negative的距离为d(a, n)。我们尽可能地希望L = d(a, p) - d(a, n)尽可能小。
更具体的,我们希望L=max(d(a, p) - d(a, n)+margin, 0)尽可能小,但是取非0损失。margin为一个大于0的常数。
计算Loss的时候,通常会遇到3种情况。
eazy triplet: d(a, p) +margin< d(a, n),这种情况属于理想状态,不需要计算损失并优化。很好理解,A与P的距离加上Margin还要小于A与N的距离,这样自然是不需要进一步优化的。
hard triplet: d(a, n) < d(a, p),即有没有margin作为隔离缓冲区,A与N的距离都小于A与P的距离,此时产生损失,用于反向优化网络。
semi-hard triplet: d(a, p) < d(a, n)<d(a, p) +margin,这种情况下,我们也认为需要进行优化处理。
3. Triplet公式推导
三元损失主要是用于帮助学习更好的Embedding信息,至于Embedding,大家可以认为是对应于某一个感兴趣内容的特征序列信息。
前面讲到,我们计算Triplet Loss时,会用到Anchor、Positive和Negative,此处Anchor和Positives属于同一类,Anchor和Negatives不属于同一类。对于特征损失,直观的,我们需要计算特征距离D(Anchor, Positives)和D(Anchor, Negatives)。三元损失使得Anchor和同类样本间(Positives)的距离最小化,同时使得Anchor和不同类样本(Negatives)的距离最大化。
三元损失是以一个Anchor为参照,的与其同类(相同ID,称为Positive)的样本之间距离最小化,同时与其不同类(不同ID,称为Negative)样本之间的距离最大化。因此,Triplet-Loss的数学表达式如下。

进一步,损失函数描述如下。
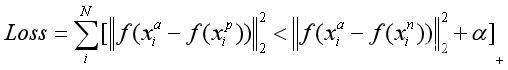
对margin的理解
Margin本身并不神秘,只是添加了作为一个缓冲地带。保证A与P的距离更小,A与N的距离更大。同时,Margin的引入还解决了D(A, P)与D(A, N)相同的问题。如前面所述,损失可以表示为
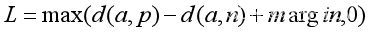
如果不添加Margin,就转换成了L = max(d(a, p) - d(a, n), 0)。
搜索positive和negative样本
那么,我们如何搜索那些事positive,哪些是negative样本呢?
首先我们需要确认的是,我们对于训练数据的读入,以遵循一定的规则的。比如我们需要导入4个不同ID的Person, 同时每一个ID都取4张图像。也就是说,我们一共取16幅图像用于训练,包含4个ID,及四个不同的Person,每个ID(Person)包含4幅不同时空的图像。如此一来,我们在一个训练iteration中,用于训练的既有Positive,又有Negative。
4. WGN中的Triplet Loss
计算Triplet Loss时,首先需要计算出每一个特征与其他特征之间的欧氏距离。如图所示,为WGN提供的Triplet Loss计算代码。

输入inputs的shape为shape(batch_size, feat_dim),其中feat_dim为特征维数。第10行是先给batch中的各图片执行平方计算,并将平方和扩充为shape(batch_size, batch_size)。
计算距离
第11行是计算一个batch中不同图片的特征求和。即实现如下操作。

第13行和14行执行计算平方差,开方操作和阶段操作,名副其实的欧式距离了。
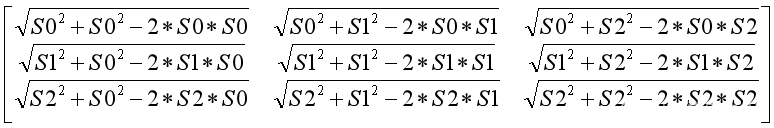
搜索Positive和Negative
从第16行开始,我们就需要搜索Positive和Negative样本了。
第16行明显是在针对计算每一张训练的image找与其属于同一类(同一个ID)的目标。
第18、19、20行就是遍历每一张训练图片,将自身作为Anchor,找到与其同类(Positive)的最远距离,找到与其不同类(Negative)的最近距离。
最后式计算一个MarginRankingLoss。至于MarginRankingLoss,大家可以取搜一下,讲解随处可见,此处不做赘述了。其Loss计算表达式如下。
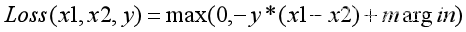
其中,y取值为1或-1。
相关文章:
ReID网络:MGN网络(4) - Loss计算
1. MGN Loss MGN采用三元损失(Triplet Loss)。 三元损失主要用于ReID算法,目的是帮助网络学习到一个好的Embedding信息。之所以称之为三元损失,主要原因在于在训练中,参与计算Loss的分别有Anchor、Positive和Negative三方。 2. Triplet Lo…...
CountDownLatch、Semaphore详解——深入探究CountDownLatch、Semaphore源码
这篇文章将会详细介绍基于AQS实现的两个并发类CountDownLatch和Semaphore,通过深入底层源代码讲解其具体实现。 目录 CountDownLatch countDown() await() Semaphore Semaphore类图 Semaphore的应用场景 acquire() tryAcquire() CountDownLatch /*** A synchroni…...
windows生成ios证书的方法
使用hbuilderx的uniapp框架开发ios应用,在测试阶段和发布阶段,需要ios证书进行打包,云打包的界面提供了生成ios证书的教程,但是教程令人很失望,它只能使用mac电脑来生成ios证书。假如没有mac电脑,就无法安照…...

【小沐学Unity3d】3ds Max 骨骼动画制作(Physique 修改器)
文章目录 1、简介2、Physique 工作流程3、Physique 对象类型4、Physique 增加骨骼5、Physique 应用和初始化6、Physique 顶点子对象7、Physique 封套子对象8、设置关键点和自动关键点模式的区别8.1 自动关键点8.2 设置关键点 结语 1、简介 官方网址: https://help.…...

生态项目|Typus如何用Sui特性制作动态NFT为DeFi赋能
对于许多人来说,可能因其涉及的期权、认购和价差在内的DeFi而显得晦涩难懂,但Typus Finance找到了一种通过动态NFT使体验更加丰富的方式。Typus NFT系列的Tails为用户带来一个外观逐渐演变并在平台上提升活动水平时获得新特权的角色。 Typus表示&#x…...

IOS打包上架AppStore被驳回信息记录
1:错误码5.2.1错误信息如下 Your app includes content or features from 公司名, or is marketed to control external hardware from 公司名, without the necessary authorization. The inclusion of third-party content within your app, whether retrieved fr…...

【Python自学笔记】Python好用的模块收集(持续更新...)
文章目录 日志模块钉钉机器人命令助手持续更新中,如果您有其他实用好用的模块欢迎留言...日志模块 写代码离不开日志,自定义一个理想的日志对于小白来说可能是一件很反锁的事情,就像我刚学习Python的时候自己写的一个自定义日志,为了解决这个痛点,今天就和大家分享一个可以…...
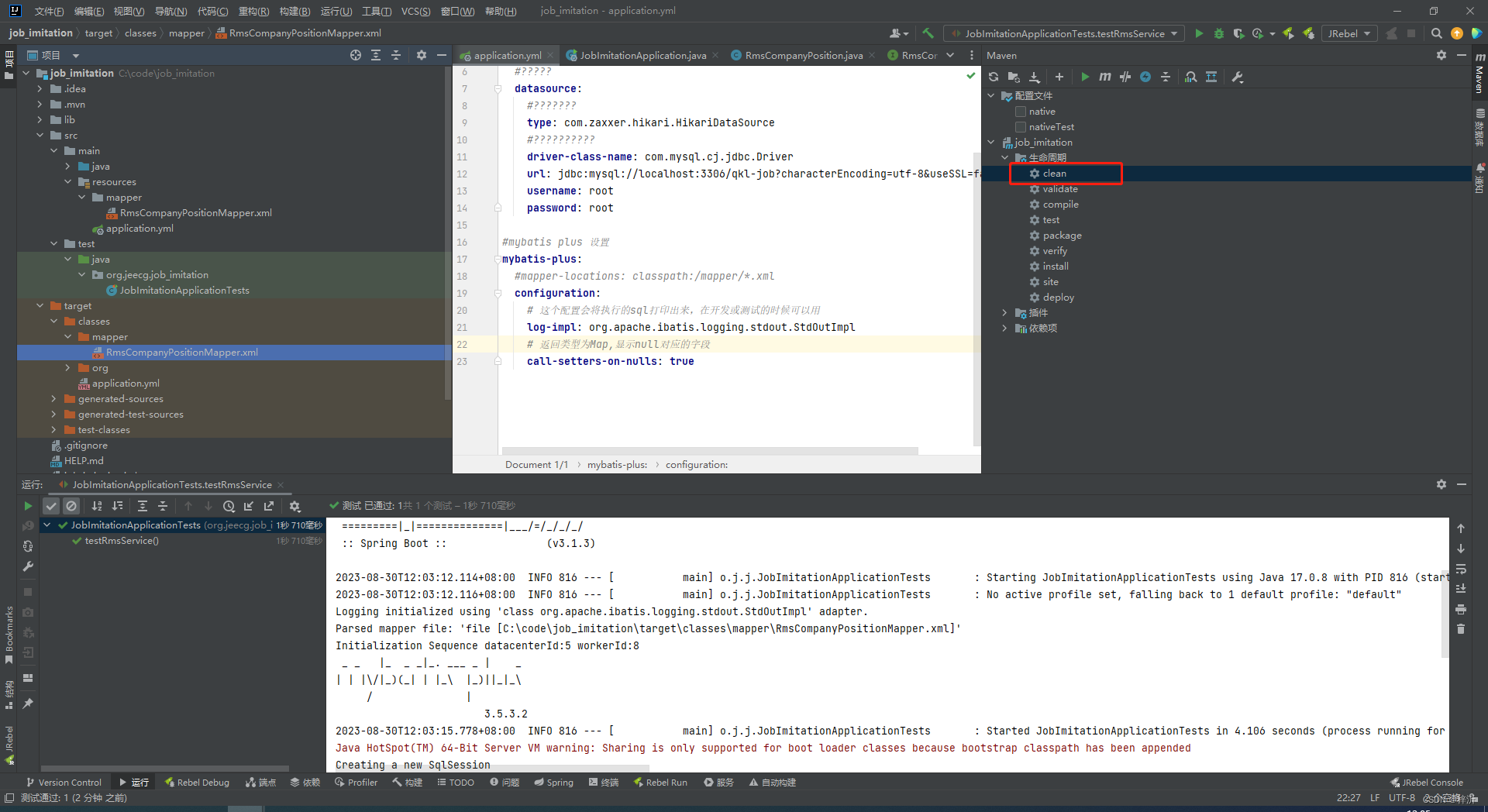
在springboot中配置mybatis(mybatis-plus)mapper.xml扫描路径的问题
我曾经遇到过类似问题: mybatis-plus的mapper.xml在src/main/java路径下如何配置pom.xml和application.yml_idea 把mapper文件放到java下如何配置_梓沂的博客-CSDN博客 当时只是找到解决问题的办法,但对mybatis配置来龙去脉并未深入了解,所…...

c++搜索剪枝常见方法与技巧
目录 搜索剪枝常见方法与技巧 关键字 搜索方法,剪枝 摘要 正文 小结 程序 参考书目 搜索剪枝常见方法与技巧 关键字 搜索方法,剪枝 摘要 搜索是计算机解题中常用的方法,它实质上是枚举法的应用。由于它相当于枚举法,所以其效率是相当地的。因此…...
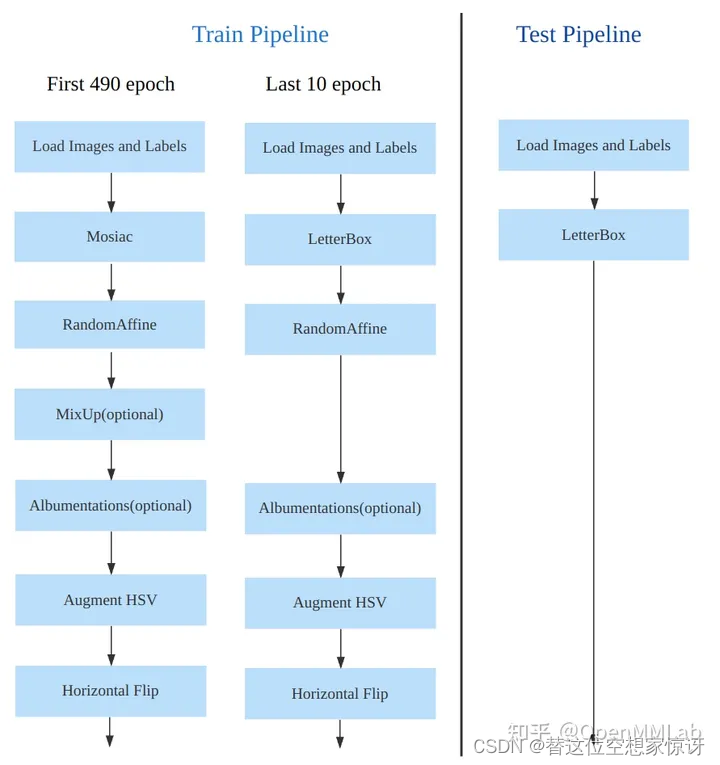
YOLO V5 和 YOLO V8 对比学习
参考文章: 1、YOLOv5 深度剖析 2、如何看待YOLOv8,YOLOv5作者开源新作,它来了!? 3、anchor的简单理解 完整网络结构 YOLO v5和YOLO v8的Head部分 YOLO v8的Head 部分相比 YOLOv5 改动较大,换成了目前主流的解耦头结构…...
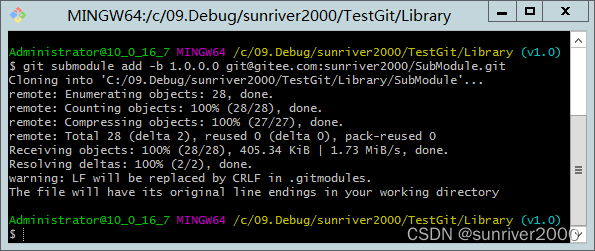
【Git】(六)子模块跟随主仓库切换分支
场景 主仓库:TestGit 子模块:SubModule 分支v1.0 .gitmodules文件 [submodule "Library/SubModule"]path Library/SubModuleurl gitgitee.com:sunriver2000/SubModule.gitbranch 1.0.0.0 分支v2.0 .gitmodules文件 [submodule "Li…...

开源的经济影响:商业与社区的平衡
🌷🍁 博主猫头虎 带您 Go to New World.✨🍁 🦄 博客首页——猫头虎的博客🎐 🐳《面试题大全专栏》 文章图文并茂🦕生动形象🦖简单易学!欢迎大家来踩踩~🌺 &a…...

数据库复习整理
1.group by与where 一,group by 字句也和where条件语句结合在一起使用。当结合在一起时,where在前,group by 在后。 即先对select xx from xx的记录集合用where进行筛选,然后再使用group by 对筛选后的结果进行分组 使用having字句…...
开始MySQL之路——MySQL安装和卸载
MySQL的介绍 MySQL数据库管理系统由瑞典的DataKonsultAB公司研发,该公司被Sun公司收购,现在Sun公司又被Oracle公司收购,因此MySQL目前属于Oracle旗下产品。 MySQL所使用的SQL语言是用于访问数据库的最常用标准化语言。MySQL软件采用了双授权…...

pxe网络装机
PXE是什么? 批量装机系统,网络安装linux操作系统。需要客户端的网卡支持pxe网络启动。 PXE的组件: vsftpd/httpd/nfs 负责提供系统的安装文件 tftp 负责提供系统安装前的引导文件与内核文件 dhcp 负责提供客户端的IP地址分配与pxe引…...
【数据库事务】
数据库事务 何为事务事务的特性原子性 Atomicity一致性 Consistency隔离性 IsolationRead UncommittedRead CommittedRepeatable ReadSerializable 持久性 Durability功能快捷键合理的创建标题,有助于目录的生成如何改变文本的样式插入链接与图片如何插入一段漂亮的…...

Apache Tomcat
在Java中,如果您想使用 Apache Tomcat 作为服务器容器,您需要从 Apache Tomcat 官方网站(https://tomcat.apache.org)下载并导入 Tomcat 的相关 JAR 文件。 以下是使用 Tomcat 类创建和配置 Tomcat 服务器的示例代码:…...

python类
python是一种面向对象的变成语言。 python几乎所有的东西都是对象,包括对象和属性。 一.类的定义 python类的定义: class ClassName:pass: 实例: 注意: 类中的函数称为方法,有关于函数的一切适用于方法&…...

SpringBoot + layui 框架实现一周免登陆功能
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

如何使用Unity制作一个国际象棋
LinnoChess1.0 该项目旨在做一些Unity小游戏项目开发来练练手 如果有更新建议请私信RWLinno 项目地址:https://github.com/RWLinno/LinnoChess 目前效果 能够正常下棋;能够编辑棋盘;能够SL棋局;能够记录棋谱;能够显…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

如何配置一个sql server使得其它用户可以通过excel odbc获取数据
要让其他用户通过 Excel 使用 ODBC 连接到 SQL Server 获取数据,你需要完成以下配置步骤: ✅ 一、在 SQL Server 端配置(服务器设置) 1. 启用 TCP/IP 协议 打开 “SQL Server 配置管理器”。导航到:SQL Server 网络配…...
