c++搜索剪枝常见方法与技巧
目录
搜索剪枝常见方法与技巧
关键字 搜索方法,剪枝
摘要
正文
小结
程序
参考书目
搜索剪枝常见方法与技巧
关键字 搜索方法,剪枝
摘要
搜索是计算机解题中常用的方法,它实质上是枚举法的应用。由于它相当于枚举法,所以其效率是相当地的。因此,为了提高搜索的效率,人们想出了很多剪枝的方法,如分枝定界,启发式搜索等等。在竞赛中,我们不仅要熟练掌握这些方法,而且要因地制宜地运用一些技巧,以提高搜索的效率。
正文
搜索的效率是很低的,即使剪枝再好,也无法弥补其在时间复杂度上的缺陷。因此,在解题中,除非其他任何方法都行不通,才可采用搜索。
既然采用了搜索,剪枝就显得十分的必要,即使就简简单单的设一个槛值,或多加一两条判断,就可对搜索的效率产生惊人的影响。例如N后问题,假如放完皇后再判断,则仅仅只算到7,就开始有停顿,到了8就已经超过了20秒,而如果边放边判断,就算到了10,也没有停顿的感觉。所以,用搜索就一定要剪枝。
剪枝至少有两方面,一是从方法上剪枝,如采用分枝定界,启发式搜索等,适用范围比较广;二是使用一些小技巧,这类方法适用性虽不如第一类,有时甚至只能适用一道题,但也十分有效,并且几乎每道题都存在一些这样那样的剪枝技巧,只是每题有所不同而已。
问题一:(最短编号序列)
表A和表B各含k(k<=20)个元素,元素编号从1到k。两个表中的每个元素都是由0和1组成的字符串。(不是空格)字符串的长度<=20。例如下表的A和B两个表,每个表都含3个元素(k=3)。
| 元素编号 | 字符串 |
| 1 | 1 |
| 2 | 10111 |
| 3 | 10 |
表A 表B
| 元素编号 | 字符串 |
| 1 | 111 |
| 2 | 10 |
| 3 | 0 |
对于表A和表B,存在一个元素编号的序列2113,分别用表A中的字符串和表B 中的字符串去置换相应的元素编号,可得相同的字符串序列101111110,见下表。
| 元素编号序列 | 2 | 1 | 1 | 3 |
| 用表A的字符串替换 | 10111 | 1 | 1 | 10 |
| 用表B的字符串替换 | 10 | 111 | 111 | 0 |
对表A和表B,具有上述性质的元素编号序列称之为S(AB)。对于上例S(AB)=2113。
编写程序:从文件中读入表A和表B的各个元素,寻找一个长度最短的具有上述性质的元素编号序列S(AB)。(若找不到长度<=100的编号序列,则输出“No Answer”。
对于这道题,因为表A和表B不确定,所以不可能找到一种数学的方法。因为所求的是最优解,而深度优先搜索很容易进入一条死胡同而浪费时间,所以必须采用广度优先搜索的方法。但是,广度优先搜索也有其缺陷。当表A和表B中的元素过多是,扩展的结点也是相当多的,搜索所耗费的时间也无法达到测试的要求。为了解决这个问题,就必须对搜索的算法加以改进。分枝限界似乎不行,因为无法确定代价。而且,由于目标不确定,也无法设定估价函数。但是,因为此题的规则既可以正向使用,又可以逆向使用,于是便可以采用双向搜索。
在大方法确定后,算法的框架就已经基本形成,但即使如此,算法也还有可改进的地方。
- 存储当前的A串和B串是很费空间的,但因为A串和B串的大部分相同,故只需记录不同部分,并作个标记。再换成动态存储。
- 为了保证两个方向扩展结点的速度相对平衡,可以采取每次扩展结点数较少的方向,而不是两方向轮流扩展。
如此一来,搜索的效率就比单纯的广度优先搜索有了明显的提高。
(附程序sab.pas)
有时,搜索也会有不同的搜索方法(如多处理机调度问题),也会产生不同的效率。
问题二:(任务安排)
N个城市,若干城市间有道路相连,一辆汽车在城市间运送货物,总是从城市1出发,又回到城市1。该车每次需完成若干个任务,每个任务都是要求该车将货物从一个城市运送至另一个。例如若要完成任务2->6,则该车一次旅程中必含有一条子路径。先到2,再到6。
如下图所示,如果要求的任务是2->3,2->4,3->1,2->5,6->4,则一条完成全部任务的路径是1->2->3->1->2->5->6->4->1。











4
1 2 6
5
3 7
编程由文件读入道路分布的领接矩阵,然后对要求完成的若干任务,寻找一条旅行路线,使得在完成任务最多的前提下,经过的城市总次数最少。如上例中经过城市总次数为8,城市1和2各经过2次均以2次计(起点不计),N<60。
这道题,因为很难找到数学规律,便只有采用搜索的方法。
首先,第一感觉便是:从城市i出发,便搜索所有相邻的城市,再根据当前所处的城市,确定任务的完成情况,从中找到最优解。这种搜索的效率是极低的,其最大原因就在于:目标不明确。
根据题意,我们只需到达需上货和下货的城市,其它的城市仅作为中间过程,而不应作为目标。因此,首先必须确定可能和不可能完成的任务,然后求出任意两城市间的最短路径。在搜索时,就只需考虑有货要上的城市,或者是要运到该城市的货全在车上,其它不须考虑。同时,还可以设定两个简单的槛值。如果当前费用+还需达的城市>=当前最优解,或当前费用+返回城市1的费用>=当前最优解,则不需继续往下搜索。
这种方法与第一感的方法有天壤之别。(附程序travell.pas)
问题三:(多处理机调度问题)
设定有若干台相同的处理机P1,P2 Pn,和m个独立的作业J1,J2 jm,处理机以互不相关的方式处理作业,现约定任何作业可以在任何一台处理机上运行,但未完工之前不允许中断作业,作业也不能拆分成更小的作业,已知作业Ji需要处理机处理的时间为Ti(i=1,2 m)。编程完成以下两个任务:
任务一:假设有n台处理机和m个作业及其每一个作业所需处理的时间Ti存放在文件中,求解一个最佳调度方案,使得完成这m个作业的总工时最少并输出最少工时。
任务二:假设给定作业时间表和限定完工时间T于文件中,求解在限定时间T内完成这批作业所需要最少处理机台数和调度方案。
此题有两种搜索方法:
方法一:按顺序搜索每个作业。当搜索一个作业时,将其放在每台处理机搜索一次。
方法二:按顺序搜索每台处理机。当搜索一台处理机时,将每个作业放在上面搜索一次。
对比上述两种方法,可以发现:方法二较方法一更容易剪枝。
下面是两中方法剪枝的对照:
对于方法一:只能根据目前已确定的需时最长的处理机的耗时与目前最佳解比较。
对于方法二:可约定Time[1]>Time[2]>Time[3]> >Time[n](Time[i]表示第i台处理机的处理时间),从而可以设定槛值:如当前处理机的处理时间>=目前最佳解,或剩下的处理机台数×上一台处理机的处理时间<剩余的作业需要的处理时间,则回溯。因为在前面的约束条件下,已经不可能有解。
因此,从上面的比较来看,第二种方法显然是比第一种要好的。下面就针对第二种方法更深一层的进行探讨。
对于任务一,首先可以用贪心求出Time[1]的上界。然后,还可以Time[1]的下界,UP(作业总时间/处理机台数)。(UP表示大于等于该小数的最小整数)。搜索便从上界开始,找到一个解后,若等于下界即可停止搜索。
(附程序jobs_1.pas)
对于任务二,可采用深度+可变下界。下界为:UP(作业总时间/限定时间),即至少需要的处理机台数。并设定Time[1]的上界为T。
(附程序jobs_2.pas)
小结
搜索的使用相当广泛,几乎每题都可以采用搜索的方法。虽然如此,搜索也切不可滥用。只有当问题无规律可寻时,才可用搜索。一旦确定了使用搜索,就一定要想办法对其进行剪枝。无论是采用剪枝的常见方法,还是用一些搜索的小技巧,虽都无法降低搜索的时间复杂度,却总还是大有裨益的。
程序
1. 最短编号序列:sab.pas
program sab;
type aa=string[100];
ltype=record
f:integer; {父指针}
k,d,la,lb:shortint;
{k--剩余串标志,d--序列中元素的编号,la,lb--A,B两串的串长}
st:^aa; {剩余串}
end;
const maxn=1300;
var t,h:array[0..1] of integer; {h--队首指针,t--队尾指针,0表示正向,1表示逆向}
p:array[0..1,1..maxn] of ltype; {p[0]--正向搜索表,p[1]--逆向搜索表}
strs:array[1..2,1..20] of string[20]; {strs[1]--表A元素,strs[2]--表B元素}
n:integer; {表A和表B的元素个数}
procedure readp; {读入数据}
var f:text;
st:string;
i,j:integer;
begin
write('File name:');
readln(st);
assign(f,st);
reset(f);
readln(f,n);
for i:=1 to n do
readln(f,strs[1,i]);
for i:=1 to n do
readln(f,strs[2,i]);
close(f);
end;
procedure print(q,k:integer); {从k出发,输出沿q方向搜索的元素编号}
begin
if k<>1 then begin
if q=1 then
writeln(p[q,k].d);
print(q,p[q,k].f);
if q=0 then
writeln(p[q,k].d);
end;
end;
procedure check(q:shortint); {判断两方向是否重合,q表示刚产生结点的方向的相反方向}
var i:integer;
begin
for i:=1 to t[1-q]-1 do
if (p[q,t[q]].k<>p[1-q,i].k) and (p[q,t[q]].st^=p[1-q,i].st^) and
(p[q,t[q]].la+p[1-q,i].la<=100) and (p[q,t[q]].lb+p[1-q,i].lb<=100)
then begin
if q=0 then
begin
print(0,t[q]);
print(1,i);
end
else begin
print(0,i);
print(1,t[q]);
end;
halt;
end;
end;
procedure find(q:shortint); {沿q方向扩展一层结点}
var i:integer;
sa,sb:aa;
begin
for i:=1 to n do
if (p[q,h[q]].la+length(strs[1,i])<=100) and
(p[q,h[q]].lb+length(strs[2,i])<=100) then
begin
sa:='';sb:='';
if p[q,h[q]].k=1
then sa:=p[q,h[q]].st^
else sb:=p[q,h[q]].st^;
if q=0 then {沿不同方向将编号为i的元素加到序列中}
begin
sa:=sa+strs[1,i];
sb:=sb+strs[2,i];
while (sa<>'') and (sb<>'') and (sa[1]=sb[1]) do
begin
delete(sa,1,1);
delete(sb,1,1);
end
end
else begin
sa:=strs[1,i]+sa;sb:=strs[2,i]+sb;
while (sa<>'') and (sb<>'') and
(sa[length(sa)]=sb[length(sb)]) do
begin
delete(sa,length(sa),1);
delete(sb,length(sb),1);
end;
end;
if (sa='') or (sb='') then {生成一个新的结点}
with p[q,t[q]] do
begin
f:=h[q];d:=i;
la:=p[q,h[q]].la+length(strs[1,i]);
lb:=p[q,h[q]].lb+length(strs[2,i]);
new(st);
if sa='' then
begin
k:=2;st^:=sb
end
else begin
k:=1;st^:=sa;
end;
check(q);
inc(t[q]);
end;
end;
inc(h[q]);
end;
begin
readp;
h[0]:=1;h[1]:=1;
t[0]:=2;t[1]:=2;
new(p[0,1].st);p[0,1].st^:='';
new(p[1,1].st);p[1,1].st^:='';
{队列初始化}
while (h[0]<t[0]) and (h[1]<t[1]) and (t[0]<maxn) and (t[1]<maxn) do
if t[0]<t[1] {比较两方向的节点数,向结点数少的方向扩展}
then find(0)
else find(1);
writeln('No answer!');
end.
- 任务安排:travell.pas
program travell;
var path, {path[i,j]--以i为起点第j个运输终点}
next, {next[i,j]--从i到j的最短路径中,i顶点的下一个顶点}
dist, {dist[i,j]--从i到j的最短路径长度}
road:array[1..60,1..60] of integer; {道路的邻接矩阵}
head, {head[i]--以i为起点的任务数}
tail, {tail[i]--0表示以i为终点无任务或已完成}
{1表示以i为终点的任务的所有顶点都在完成任务路径中}
{k+1表示以i为终点的所有任务,还有k个顶点未到达}
arrive:array[1..60] of integer; {arrive[i]--顶点i的经过次数}
d, {完成任务路径}
bestd:array[1..100] of integer; {当前最佳完成任务路径}
left, {必经结点个数}
cost, {当前代价}
mincost, {最佳完成任务代价}
s, {经过顶点数}
bests, {最佳完成任务所经过的顶点数}
m, {任务数}
n:integer; {城市数}
procedure findshortest; {求任意两点间的最短路径}
var i,j,k:integer;
begin
for i:=1 to n do
for j:=1 to n do
if road[i,j]=1 then
begin
dist[i,j]:=1;
next[i,j]:=j
end
else dist[i,j]:=100;
for k:=1 to n do
for i:=1 to n do
for j:=1 to n do
if dist[i,k]+dist[k,j]<dist[i,j] then
begin
dist[i,j]:=dist[i,k]+dist[k,j];
next[i,j]:=next[i,k];
end;
end;
procedure init; {读入数据并初始化数据}
var i,j,k:integer;
st:string;
f:text;
begin
write('File name:');
readln(st);
assign(f,st);
reset(f);
readln(f,n);
for i:=1 to n do
for j:=1 to n do
read(f,road[i,j]);
findshortest;
readln(f,m);
for i:=1 to m do
begin
read(f,j,k);
if (dist[1,j]<100) and (dist[1,k]<100) then
begin
inc(head[j]);
inc(tail[k]);
path[j,head[j]]:=k;
end;
end;
close(f);
for i:=1 to m do
if tail[i]>0 then
inc(tail[i]);
for i:=1 to head[1] do
dec(tail[path[1,i]]);
head[1]:=0;inc(s);d[s]:=1;left:=0;
cost:=0;mincost:=maxint;
for i:=2 to n do
if (head[i]>0) or (tail[i]>0) then
inc(left);
end;
procedure try; {搜索过程}
var i,j,k:integer;
p:boolean;
begin
if (cost+left>=mincost) or (cost+dist[1,d[s]]>=mincost) then exit;
if left=0 then {是否完成了所有任务}
begin
mincost:=cost+dist[1,d[s]];
bestd:=d;
bests:=s;
inc(bests);bestd[bests]:=1;
exit;
end;
for i:=2 to n do
if (head[i]>0) or (tail[i]=1) then {如果去i顶点有必要}
begin
inc(cost,dist[d[s],i]);
inc(arrive[i]);
inc(s);
d[s]:=i;
if arrive[i]=1 then
{如果i顶点第一次到达,则所有以i为起点的任务的终点tail值减1}
for j:=1 to head[i] do
dec(tail[path[i,j]]);
k:=head[i];
head[i]:=0;
if tail[i]=1 then
{如果完成了以i为终点的所有任务,该点则不需再经过}
begin
p:=true;
dec(tail[i]);
end
else p:=false;
if tail[i]=0 then
dec(left);
try;
{恢复递归前的数据}
if tail[i]=0 then
inc(left);
if true then
inc(tail[i]);
head[i]:=k;
if arrive[i]=1 then
for j:=1 to head[i] do
inc(tail[path[i,j]]);
dec(s);
dec(arrive[i]);
dec(cost,dist[d[s],i]);
end;
end;
procedure show(i,j:integer); {输出从i到j的最短路径}
begin
while i<>j do begin
write('-->',next[i,j]);i:=next[i,j];
end;
end;
procedure print; {输出最佳任务安排方案}
var i:integer;
begin
write(1);
for i:=1 to bests-1 do
show(bestd[i],bestd[i+1]);
writeln;
writeln('Min cost=',mincost);
end;
begin
init;
try;
print;
end.
- 多处理机调度问题:
任务一:jobs_1.pas
program jobs_1;
const maxn=100; {处理机的最多数目}
maxm=100; {作业的最多数目}
var
t:array[1..maxm] of timeint; {t[i]--处理作业i需要的时间}
time, {time[i]--第i台处理机的处理时间}
l, {l[i]--第i台处理机处理作业的数目}
l1:array[0..maxn] of timeint; {l1[i]--目前最优解中第i台处理机处理作业的数目}
a, {a[i,j]--第i台处理机处理的第j个作业耗费的时间}
a1:array[1..maxn,1..maxm] of integer;
{a1[i,j]--目前最优解中第i台处理机处理的第j个作业耗费的时间}
done:array[1..maxm] of boolean; {done[i]--true表示作业i已完成,false表示未完成}
least, {处理时间的下界}
i,j,k,n,m,
min, {目前最优解的处理时间}
rest:integer; {剩余作业的总时间}
procedure print; {输出最优解}
var i,j:integer;
begin
for i:=1 to n do
begin
write(i,':');
for j:=1 to l1[i] do
write(a1[i,j]:4);
writeln;
end;
writeln('T0=',time[0]+1);
end;
procedure readp; {读入数据}
var
f:text;
st:string;
i,j,k:integer;
begin
write('File name:');readln(st);
assign(f,st);reset(f);
readln(f,n,m);
for i:=1 to m do
begin
read(f,t[i]);inc(rest,t[i]);
end;
close(f);
least:=(rest-1) div n+1; {定下界}
for i:=1 to m-1 do {排序}
for j:=i+1 to m do
if t[j]>t[i] then
begin k:=t[i];t[i]:=t[j];t[j]:=k end;
end;
procedure try(p,q:integer); {从p--m中选取作业放到处理机q上}
var j:integer;
z:boolean;
begin
z:=true;
for j:=p to m do
if not done[j] and (time[q]+t[j]<=time[q-1]) then {选择合适的作业}
begin
z:=false;done[j]:=true;
inc(l[q]);a[q,l[q]]:=t[j];inc(time[q],t[j]);dec(rest,t[j]);
try(j+1,q);
dec(l[q]);dec(time[q],t[j]);inc(rest,t[j]);done[j]:=false;
if time[1]>time[0] then exit;
{找到解后退回处理机1,需更新time[1],使之减小到time[0]}
{2--n台处理机就不需再搜索}
end;
if z and ((n-q)*time[q]>=rest) then {如果处理机q已无法放任何作业}
if rest=0 then {找到一组解}
begin
a1:=a;l1:=l;
time[0]:=time[1]-1;
if time[1]=least then
begin print;halt end;
end
else if q<n then {继续搜索}
try(1,q+1);
end;
begin
readp;
fillchar(time,sizeof(time),0);
fillchar(a,sizeof(a),0);
fillchar(l1,sizeof(l1),0);
fillchar(l,sizeof(l),0);
for i:=1 to m do {贪心求上界}
begin
k:=1;
for j:=2 to n do
if time[j]<time[k] then k:=j;
time[k]:=time[k]+t[i];
l1[k]:=l1[k]+1;
a1[k,l1[k]]:=t[i];
end;
min:=time[1];time[0]:=min-1;
for i:=2 to n do
if time[i]>min then min:=time[i];
if min=least then {如上下界相等}
begin
print;
halt;
end;
fillchar(time,sizeof(time),0);
time[0]:=min-1; {将上界减1,以找到更优的解}
try(1,1);
print;
end.
任务二:jobs_2.pas
program jobs_2;
const maxn=100; {处理机的最多数目}
maxm=100; {作业的最多数目}
var
t:array[1..maxm] of timeint; {t[i]--处理作业i需要的时间}
time, {time[i]--第i台处理机的处理时间}
l, {l[i]--第i台处理机处理作业的数目}
l1:array[0..maxn] of timeint; {l1[i]--目前最优解中第i台处理机处理作业的数目}
a, {a[i,j]--第i台处理机处理的第j个作业耗费的时间}
a1:array[1..maxn,1..maxm] of integer;
{a1[i,j]--目前最优解中第i台处理机处理的第j个作业耗费的时间}
done:array[1..maxm] of boolean; {done[i]--true表示作业i已完成,false表示未完成}
least, {处理时间的下界}
i,j,k,tmax,m,
min, {目前最优解的处理时间}
rest:integer; {剩余作业的总时间}
procedure print; {输出最优解}
var i,j:integer;
begin
for i:=1 to least do
begin
write(i,':');
for j:=1 to l1[i] do
write(a1[i,j]:4);
writeln;
end;
writeln('Min=',least);
end;
procedure readp; {读入数据}
var
f:text;
st:string;
i,j,k:integer;
begin
write('File name:');readln(st);
assign(f,st);reset(f);
readln(f,tmax,m);
for i:=1 to m do begin
read(f,t[i]);inc(rest,t[i]);
end;
close(f);
least:=(rest-1) div tmax+1; {确定下界}
for i:=1 to m-1 do {排序}
for j:=i+1 to m do
if t[j]>t[i] then
begin k:=t[i];t[i]:=t[j];t[j]:=k end;
end;
procedure try(p,q:integer); {从p--m中选取作业放到处理机q上}
var j:integer;
z:boolean;
begin
z:=true;
for j:=p to m do
if not done[j] and (time[q]+t[j]<=time[q-1]) then {找到合适的作业}
begin
z:=false;done[j]:=true;
inc(l[q]);a[q,l[q]]:=t[j];inc(time[q],t[j]);dec(rest,t[j]);
try(j+1,q);
dec(l[q]);dec(time[q],t[j]);inc(rest,t[j]);done[j]:=false;
end;
if z and ((least-q)*time[q]>=rest) then {如果处理机q已无法放任何作业}
if rest=0 then {找到最优解}
begin
a1:=a;l1:=l;
print;halt
end
else if q<min then {继续搜索}
try(1,q+1);
end;
begin
readp;
for i:=1 to m do {判断无解情况,即某一任务所需时间超过规定时间}
if t[i]>tmax then
begin writeln('No answer!');exit end;
repeat
fillchar(time,sizeof(time),0);
fillchar(l,sizeof(l),0);
fillchar(l1,sizeof(l1),0);
for i:=1 to m do {贪心求上界}
begin
k:=1;
for j:=2 to least do
if time[j]<time[k] then k:=j;
time[k]:=time[k]+t[i];
l1[k]:=l1[k]+1;
a1[k,l1[k]]:=t[i];
end;
min:=time[1];
for i:=2 to least do
if time[i]>min then min:=time[i];
if min=least then {如果贪心得出了最优解}
begin
print;halt;
end;
fillchar(time,sizeof(time),0);
time[0]:=tmax;
try(1,1);
inc(least); {下界加一}
until least>m;
print;
end.
参考书目
- 《国际国内青少年信息学(计算机)奥林匹克竞赛试题解析(1994-1995》,吴文虎,王建德主编,清华大学出版社。
- 《奥林匹克计算机(信息学)入门》,江文哉主编,上海交通大学出版社。
相关文章:

c++搜索剪枝常见方法与技巧
目录 搜索剪枝常见方法与技巧 关键字 搜索方法,剪枝 摘要 正文 小结 程序 参考书目 搜索剪枝常见方法与技巧 关键字 搜索方法,剪枝 摘要 搜索是计算机解题中常用的方法,它实质上是枚举法的应用。由于它相当于枚举法,所以其效率是相当地的。因此…...
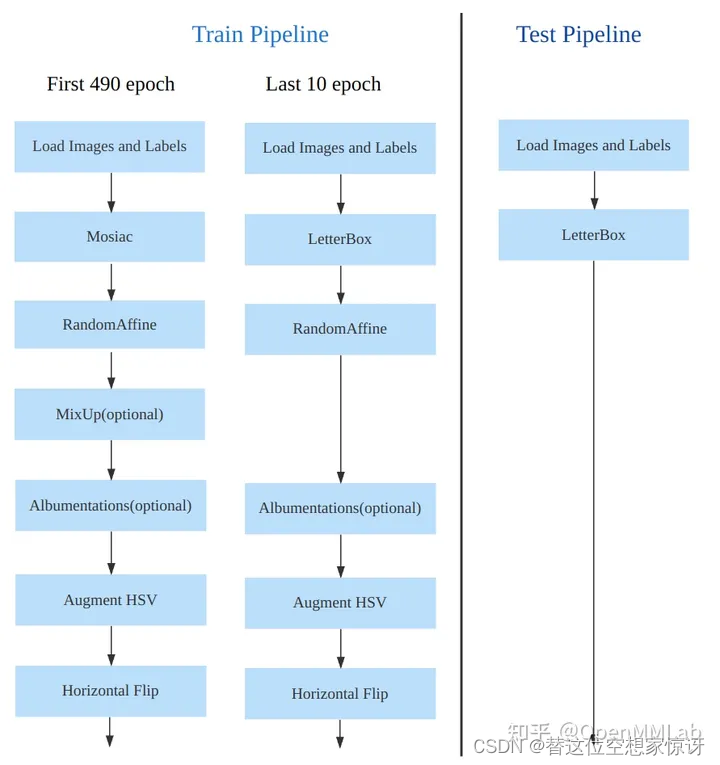
YOLO V5 和 YOLO V8 对比学习
参考文章: 1、YOLOv5 深度剖析 2、如何看待YOLOv8,YOLOv5作者开源新作,它来了!? 3、anchor的简单理解 完整网络结构 YOLO v5和YOLO v8的Head部分 YOLO v8的Head 部分相比 YOLOv5 改动较大,换成了目前主流的解耦头结构…...
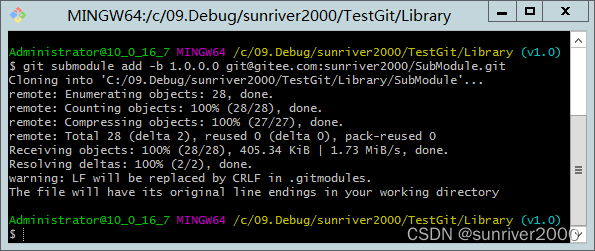
【Git】(六)子模块跟随主仓库切换分支
场景 主仓库:TestGit 子模块:SubModule 分支v1.0 .gitmodules文件 [submodule "Library/SubModule"]path Library/SubModuleurl gitgitee.com:sunriver2000/SubModule.gitbranch 1.0.0.0 分支v2.0 .gitmodules文件 [submodule "Li…...

开源的经济影响:商业与社区的平衡
🌷🍁 博主猫头虎 带您 Go to New World.✨🍁 🦄 博客首页——猫头虎的博客🎐 🐳《面试题大全专栏》 文章图文并茂🦕生动形象🦖简单易学!欢迎大家来踩踩~🌺 &a…...

数据库复习整理
1.group by与where 一,group by 字句也和where条件语句结合在一起使用。当结合在一起时,where在前,group by 在后。 即先对select xx from xx的记录集合用where进行筛选,然后再使用group by 对筛选后的结果进行分组 使用having字句…...
开始MySQL之路——MySQL安装和卸载
MySQL的介绍 MySQL数据库管理系统由瑞典的DataKonsultAB公司研发,该公司被Sun公司收购,现在Sun公司又被Oracle公司收购,因此MySQL目前属于Oracle旗下产品。 MySQL所使用的SQL语言是用于访问数据库的最常用标准化语言。MySQL软件采用了双授权…...

pxe网络装机
PXE是什么? 批量装机系统,网络安装linux操作系统。需要客户端的网卡支持pxe网络启动。 PXE的组件: vsftpd/httpd/nfs 负责提供系统的安装文件 tftp 负责提供系统安装前的引导文件与内核文件 dhcp 负责提供客户端的IP地址分配与pxe引…...
【数据库事务】
数据库事务 何为事务事务的特性原子性 Atomicity一致性 Consistency隔离性 IsolationRead UncommittedRead CommittedRepeatable ReadSerializable 持久性 Durability功能快捷键合理的创建标题,有助于目录的生成如何改变文本的样式插入链接与图片如何插入一段漂亮的…...

Apache Tomcat
在Java中,如果您想使用 Apache Tomcat 作为服务器容器,您需要从 Apache Tomcat 官方网站(https://tomcat.apache.org)下载并导入 Tomcat 的相关 JAR 文件。 以下是使用 Tomcat 类创建和配置 Tomcat 服务器的示例代码:…...

python类
python是一种面向对象的变成语言。 python几乎所有的东西都是对象,包括对象和属性。 一.类的定义 python类的定义: class ClassName:pass: 实例: 注意: 类中的函数称为方法,有关于函数的一切适用于方法&…...

SpringBoot + layui 框架实现一周免登陆功能
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

如何使用Unity制作一个国际象棋
LinnoChess1.0 该项目旨在做一些Unity小游戏项目开发来练练手 如果有更新建议请私信RWLinno 项目地址:https://github.com/RWLinno/LinnoChess 目前效果 能够正常下棋;能够编辑棋盘;能够SL棋局;能够记录棋谱;能够显…...
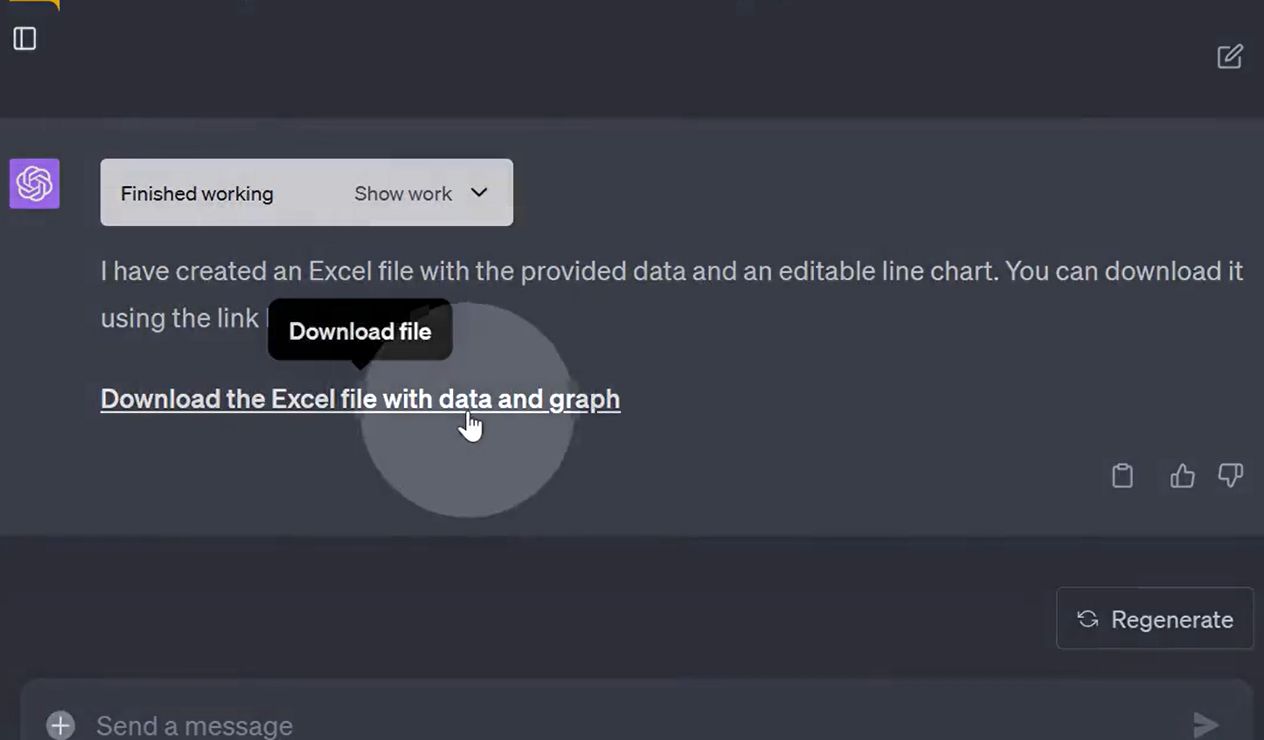
下岗吧,Excel
ChatGPT的诞生使Excel公式变得过时。通过使用 ChatGPT 的代码解释器你可以做到: 分析数据创建图表 这就像用自然语言与电子表格交谈一样。我将向大家展示如何使用 ChatGPT 执行此操作并将结果导出为Excel格式: 作为示例,我将分析并创建美国…...
黑马点评环境搭建导入
一开始配置maven的时候,发现怎么都无法查看maven的版本,后来才知道是JAVA_HOME的问题,开头多了一个空格(因为我是直接复制过去的),然后搜网上通过命令行可以看到肉眼看不到的bug。 通过命令行的方式改正确后…...
交换机端口安全
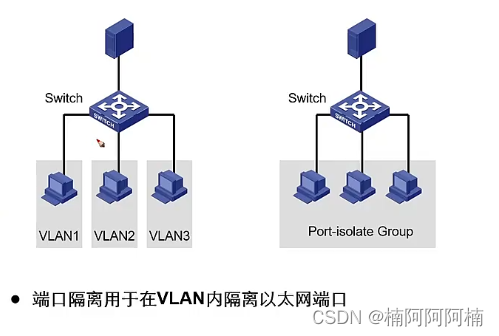
文章目录 一、802.1X认证1. 定义和起源2. 认证方式本地认证远程集中认证 3. 端口接入控制方式基于端口认证基于MAC地址认证 二、端口隔离技术1. 隔离组2. 隔离原理3. 应用场景 首先可以看下思维导图,以便更好的理解接下来的内容。 一、802.1X认证 1. 定义和起源 8…...

【力扣】63. 不同路径 II <动态规划>
【力扣】63. 不同路径 II 一个机器人位于一个 m m m x n n n 网格的左上角 (起始点在下图中标记为 “Start” )。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。 现在考虑网格…...
【Linux】JumpServer 堡垒机远程访问
文章目录 前言1. 安装Jump server2. 本地访问jump server3. 安装 cpolar内网穿透软件4. 配置Jump server公网访问地址5. 公网远程访问Jump server6. 固定Jump server公网地址 前言 JumpServer 是广受欢迎的开源堡垒机,是符合 4A 规范的专业运维安全审计系统。JumpS…...

WebGPT VS WebGPU
推荐:使用 NSDT编辑器 快速搭建3D应用场景 随着WebGPU的引入,Web开发发生了有趣的转变,WebGPU是一种新的API,允许Web应用程序直接访问设备的图形处理单元(GPU)。这种发展意义重大,因为 GPU 擅长…...
【Flutter】Flutter 使用 collection 优化集合操作
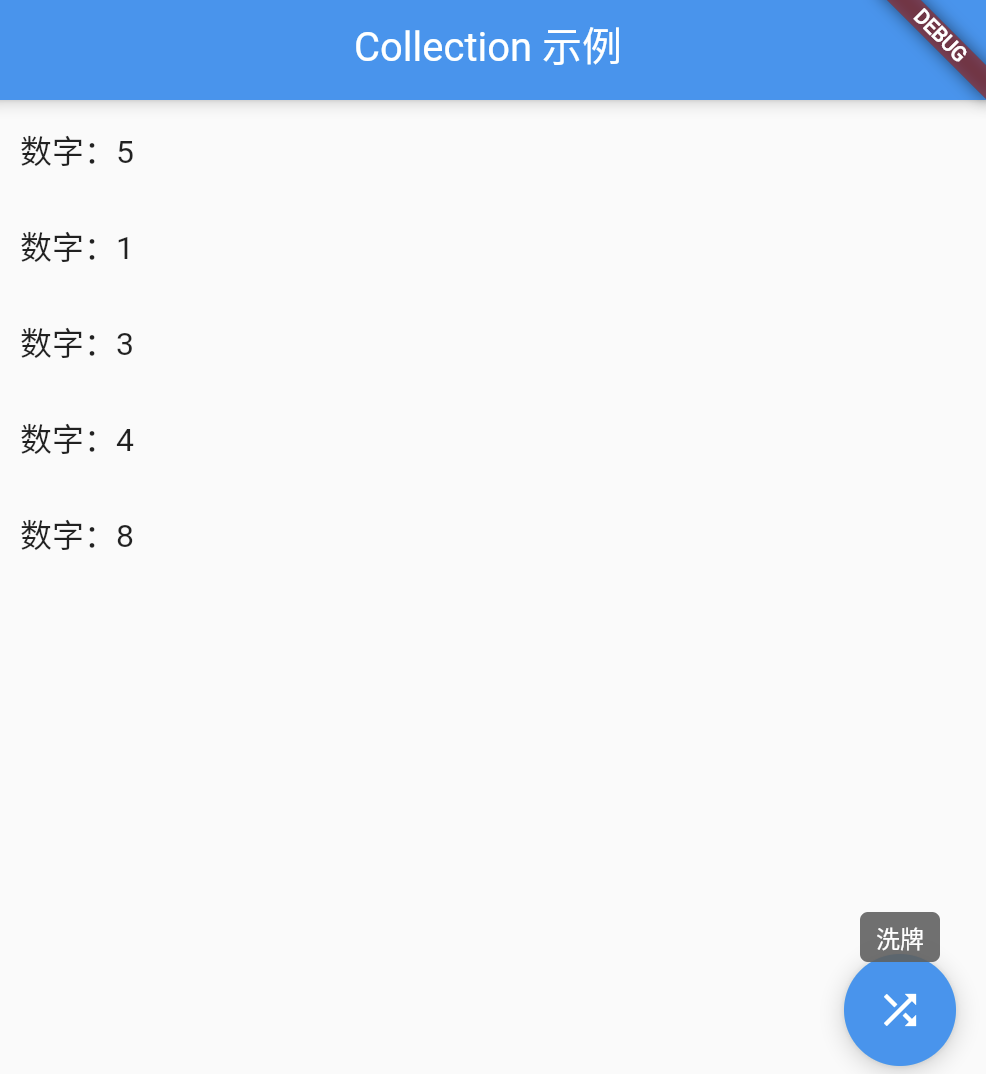
【Flutter】Flutter 使用 collection 优化集合操作 文章目录 一、前言二、安装和基本使用三、算法介绍四、如何定义相等性五、Iterable Zip 的使用六、优先队列的实现和应用七、包装器的使用八、完整示例九、总结 一、前言 大家好!我是小雨青年,今天我要…...
【核心复现】基于合作博弈的综合能源系统电-热-气协同优化运行策略(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...
