【力扣】63. 不同路径 II <动态规划>
【力扣】63. 不同路径 II
一个机器人位于一个 m m m x n n n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?网格中的障碍物和空位置分别用 1 和 0 来表示。
示例 1:
| 起点 | 0 | 0 |
|---|---|---|
| 0 | 障碍 | 0 |
| 0 | 0 | 终点 |
输入:obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出:2
解释:3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径:
-
- 向右 -> 向右 -> 向下 -> 向下
-
- 向下 -> 向下 -> 向右 -> 向右
示例 2:
| 起点 | 障碍 |
|---|---|
| 0 | 终点 |
输入:obstacleGrid = [[0,1],[0,0]]
输出:1
提示:
m == obstacleGrid.length
n == obstacleGrid[i].length
1 <= m, n <= 100
obstacleGrid[i][j] 为 0 或 1
题解
- 确定 dp 数组以及下标的含义
dp[i][j] :表示从 (0,0) 出发,到 (i, j) 有 dp[i][j] 条不同的路径。 - 确定递推公式
想要求 dp[i][j],只能有两个方向来推导出来,即 dp[i - 1][j] 和 dp[i][j - 1]。
dp[i - 1][j] 表示是从 (0, 0) 的位置到 (i - 1, j) 有几条路径,dp[i][j - 1]同理
dp[i][j] = dp[i - 1][j] + dp[i][j - 1],因为 dp[i][j] 只有这两个方向过来。
因为有了障碍,(i, j) 如果就是障碍的话应该就保持初始状态(初始状态为0)。 - dp 数组如何初始化
dp[i][0] 一定都是1,因为从 (0, 0) 的位置到 (i, 0) 的路径只有一条,那么 dp[0][j] 也同理。
但如果 (i, 0) 这条边有了障碍之后,障碍之后(包括障碍)都是走不到的位置了,所以障碍之后的 dp[i][0] 应该还是初始值0。下标(0, j)的初始化情况同理。 - 确定遍历顺序
dp[i][j] 都是从其上方和左方推导而来 - 举例推导 dp 数组(打印 dp 数组)
public class Solution {public int uniquePathsWithObstacles(int[][] obstacleGrid) {int m = obstacleGrid.length;int n = obstacleGrid[0].length;int[][] dp = new int[m][n];//如果在起点或终点出现了障碍,直接返回0if (obstacleGrid[m - 1][n - 1] == 1 || obstacleGrid[0][0] == 1) {return 0;}//dp数组初始化,若有障碍,后面都是0for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) {dp[i][0] = 1;}for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) {dp[0][j] = 1;}//遍历顺序for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {dp[i][j] = (obstacleGrid[i][j] == 0) ? dp[i - 1][j] + dp[i][j - 1] : 0;}}return dp[m - 1][n - 1];}
}
相关文章:

【力扣】63. 不同路径 II <动态规划>
【力扣】63. 不同路径 II 一个机器人位于一个 m m m x n n n 网格的左上角 (起始点在下图中标记为 “Start” )。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。 现在考虑网格…...
【Linux】JumpServer 堡垒机远程访问
文章目录 前言1. 安装Jump server2. 本地访问jump server3. 安装 cpolar内网穿透软件4. 配置Jump server公网访问地址5. 公网远程访问Jump server6. 固定Jump server公网地址 前言 JumpServer 是广受欢迎的开源堡垒机,是符合 4A 规范的专业运维安全审计系统。JumpS…...

WebGPT VS WebGPU
推荐:使用 NSDT编辑器 快速搭建3D应用场景 随着WebGPU的引入,Web开发发生了有趣的转变,WebGPU是一种新的API,允许Web应用程序直接访问设备的图形处理单元(GPU)。这种发展意义重大,因为 GPU 擅长…...
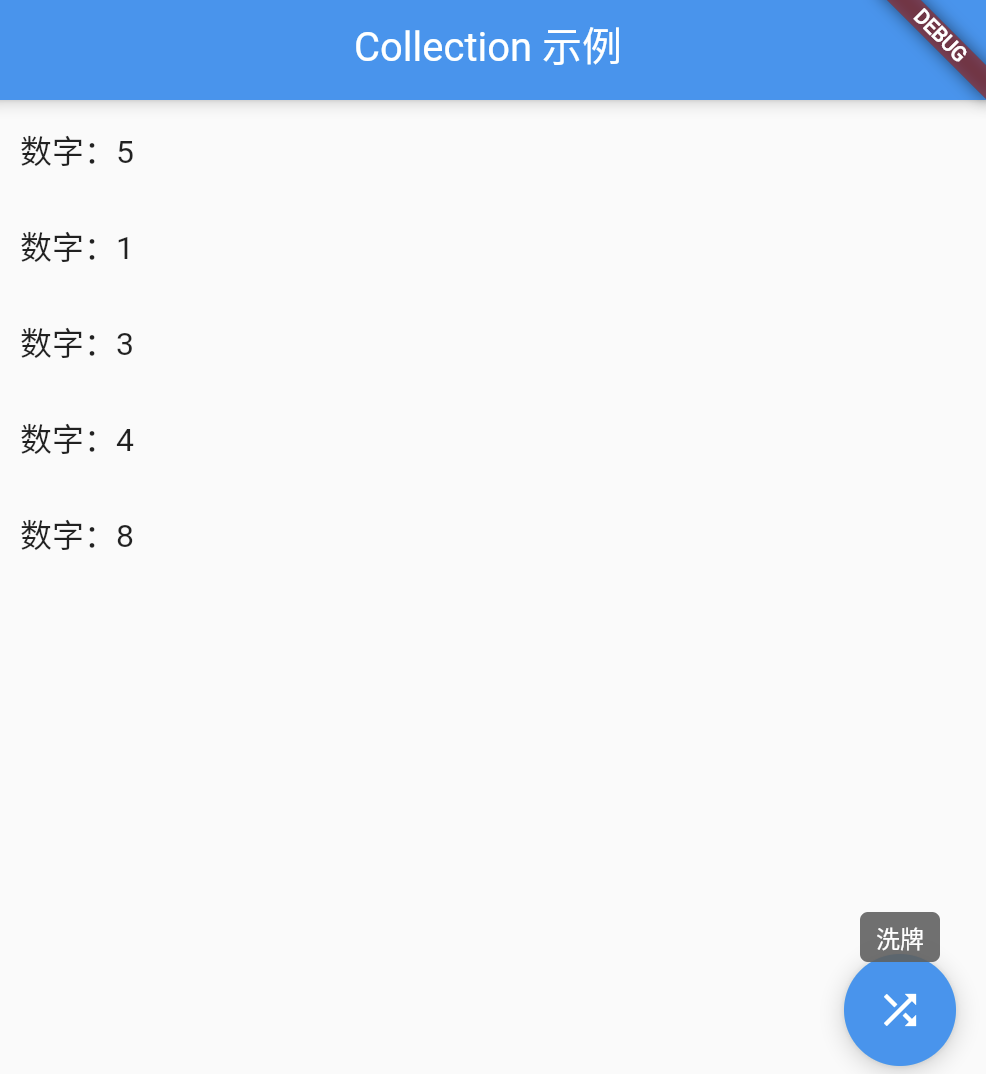
【Flutter】Flutter 使用 collection 优化集合操作
【Flutter】Flutter 使用 collection 优化集合操作 文章目录 一、前言二、安装和基本使用三、算法介绍四、如何定义相等性五、Iterable Zip 的使用六、优先队列的实现和应用七、包装器的使用八、完整示例九、总结 一、前言 大家好!我是小雨青年,今天我要…...
【核心复现】基于合作博弈的综合能源系统电-热-气协同优化运行策略(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

【设计模式】Head First 设计模式——抽象工厂模式 C++实现
设计模式最大的作用就是在变化和稳定中间寻找隔离点,然后分离它们,从而管理变化。将变化像小兔子一样关到笼子里,让它在笼子里随便跳,而不至于跳出来把你整个房间给污染掉。 设计思想 提供一个接口,让该接口负责创建一…...
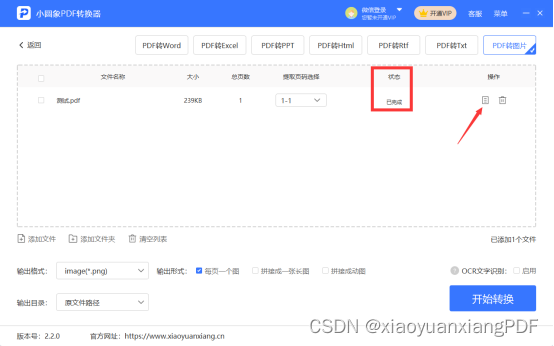
pdf怎么转换成jpg图片?
随着数字文档的广泛应用,将PDF转换为JPG图片格式成为了一个常见的需求。无论是为了在网页上展示内容,还是为了与他人分享图片,以下是一些简单的方法,帮助您将PDF文件快速转换为高质量的JPG图片。 方法一:在线PDF转JPG…...
远程访问Linux的DataEase数据可视化分析,有哪些推荐的工具?
DataEase 是开源的数据可视化分析工具,帮助用户快速分析数据并洞察业务趋势,从而实现业务的改进与优化。是开源的数据可视化分析工具,帮助用户快速分析数据并洞察业务趋势,从而实现业务的改进与优化。 在本地搭建后,借助cpolar 内…...

每日一题——旋转图像
旋转图像 题目链接 方法一:利用辅助数组 通过对示例的观察和分析,我们可以得到这样的结论: 对于原数组的下标为i行元素,顺时针旋转九十度后,都变成了下标为(n-1-i)列元素。如图所示ÿ…...

「Docker」《入门Docker:解放部署烦恼,提高开发效率》
《入门Docker:解放部署烦恼,提高开发效率》 一、引言1.1 Docker的定义和概念1.2 Docker的优势和应用场景 二、Docker基础知识2.1 Docker架构和组件2.2 Docker镜像和容器的关系2.3 Docker仓库和镜像的管理 三、安装和配置Docker环境3.1 安装Docker引擎3.2…...
)
数据结构--5.3图的遍历(广度优先遍历)
广度优先遍历: 广度优先遍历(BreadthFirstSearch),又称为广度优先搜索,简称BFS。 要实现对图的广度遍历,我们可以利用队列来实现。 void BFSTraverse(MGraph G) {int i,j;Queue Q;for(i0;i<G.numVerte…...
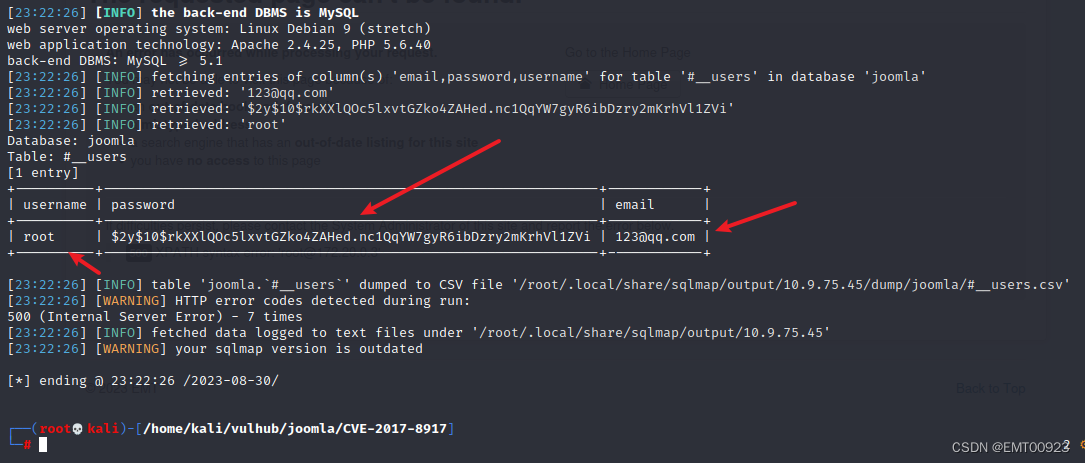
SQL注入漏洞复现(CVE-2017-8917)
文章目录 搭建环境启动环境漏洞复现报错注入使用sqlmap 前提条件: 1.安装docker docker pull medicean/vulapps:j_joomla_22.安装docker-compose docker run -d -p 8000:80 medicean/vulapps:j_joomla_23.下载vulhub Docker Compose是 docker 提供的一个命令行工具&…...
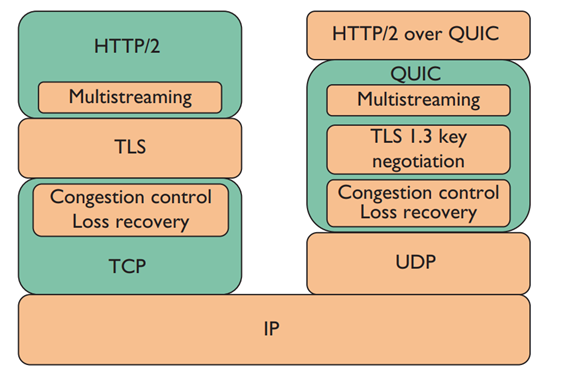
Http 1.0 1.1 2.0 3.0 版本差别
Http 1.0 发布年份:1996 非官方标准 短链接:每一次请求都对应一次TCP的连接与释放 开销大:每次请求都要TCP的连接与释放队头阻塞:每次请求都必须等上一次请求获得响应之后,才可以发送;效率低下 缓存&…...

javaee spring 依赖注入之复杂类型的注入数组 集合 等
spring 依赖注入之复杂类型的注入 package com.test.pojo;import java.util.List; import java.util.Map; import java.util.Properties;/*** description:* projectName:testSpring* see:com.test.pojo* createTime:2023/8/27 14:39*/ public class AA {private int[] arr;pr…...
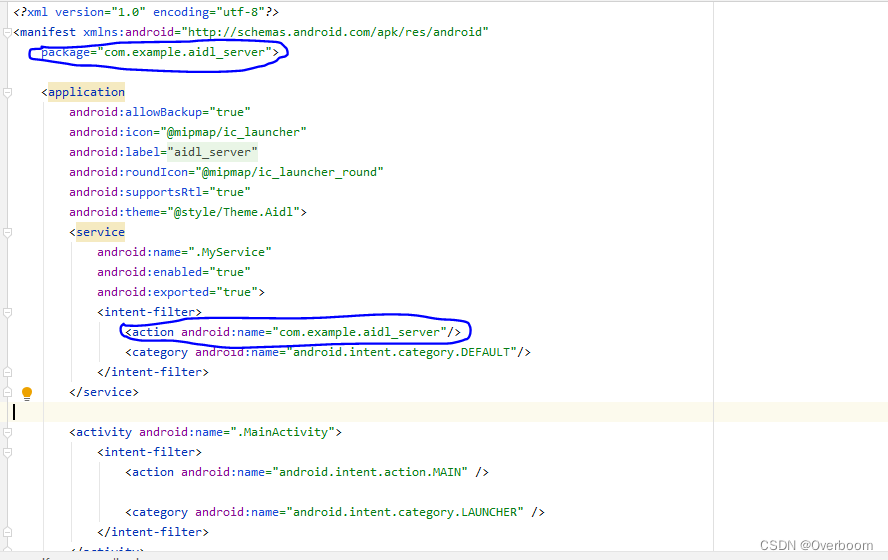
[Android AIDL] --- AIDL工程搭建
0 AIDL概念 AIDL(Android Interface Definition Language)是一种 IDL 语言,用于生成可以在 Android 设备上两个进程之间进行进程间通信(IPC)的代码。 通过 AIDL,可以在一个进程中获取另一个进程的数据和调…...

正中优配:回购!回购!再回购!已成A股新常态?
上市公司回购潮还在继续! 8月30日,海通证券、捷佳伟创等多家上市公司纷繁发布回购公告。自8月18日证监会提出“放宽相关回购条件,支撑上市公司展开股份回购”以来,A股上市公司掀起了一轮“回购潮”。Wind数据显现,8月…...
C# 多线程交替按照指定顺序执行
1.关于AutoResetEvent和ManualResetEvent的区别解释如下: AutoResetEvent和ManualResetEvent是.NET中的两个线程同步类。它们之间的主要区别在于其释放信号的方式以及对等待线程的影响。 AutoResetEvent的作用是在等待的线程被信号唤醒后,将信号自动重…...
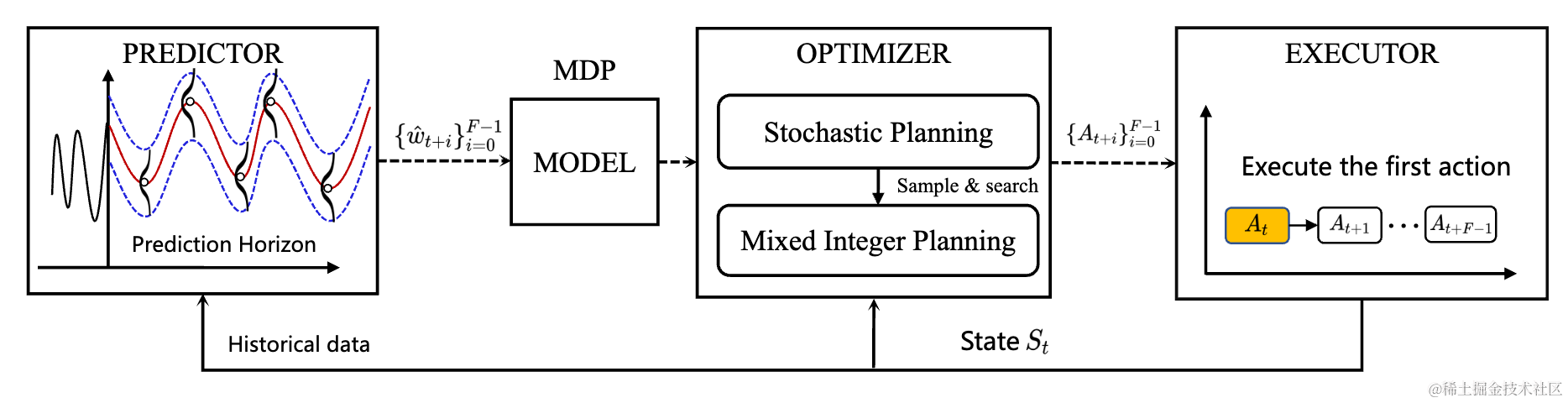
【VLDB 2023】基于预测的云资源弹性伸缩框架MagicScaler,实现“高QoS,低成本”双丰收
开篇 近日,由阿里云计算平台大数据基础工程技术团队主导,与计算平台MaxCompute团队、华东师范大学数据科学与工程学院、达摩院合作,基于预测的云计算平台资源弹性伸缩框架论文《MagicScaler: Uncertainty-aware, Predictive Autoscaling 》被…...
Node爬虫项目精简版 wallhaven网站实操 2023.8.29
练习地址: https://wallhaven.cc/toplist const express require(express); const axios require(axios); const cheerio require(cheerio); const schedule require(node-schedule); const fs require(fs);async function downloadImage(url) {const response…...

Vue统计图表的数据标签和数值显示技巧
Vue统计图表的数据标签和数值显示技巧 在开发Web应用程序时,统计图表是非常重要的数据呈现方式。Vue是一种流行的JavaScript框架,它提供了许多方便的功能来处理和展示数据。在这篇文章中,我们将探讨如何使用Vue来添加数据标签和数值显示到统…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...

rknn toolkit2搭建和推理
安装Miniconda Miniconda - Anaconda Miniconda 选择一个 新的 版本 ,不用和RKNN的python版本保持一致 使用 ./xxx.sh进行安装 下面配置一下载源 # 清华大学源(最常用) conda config --add channels https://mirrors.tuna.tsinghua.edu.cn…...

2025年低延迟业务DDoS防护全攻略:高可用架构与实战方案
一、延迟敏感行业面临的DDoS攻击新挑战 2025年,金融交易、实时竞技游戏、工业物联网等低延迟业务成为DDoS攻击的首要目标。攻击呈现三大特征: AI驱动的自适应攻击:攻击流量模拟真实用户行为,差异率低至0.5%,传统规则引…...
