每日一题——旋转图像
旋转图像
题目链接
方法一:利用辅助数组
通过对示例的观察和分析,我们可以得到这样的结论:
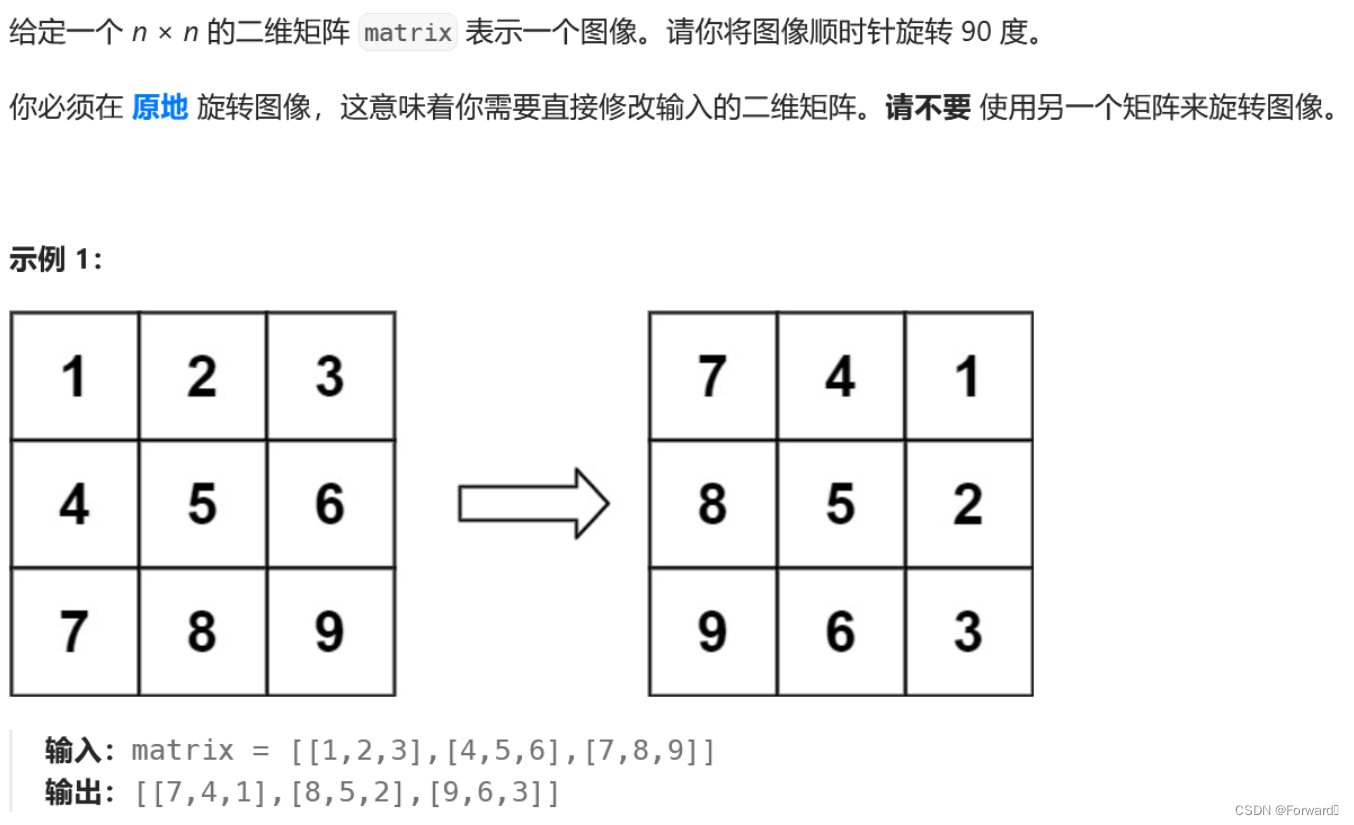
- 对于原数组的下标为
i行元素,顺时针旋转九十度后,都变成了下标为(n-1-i)列元素。如图所示:

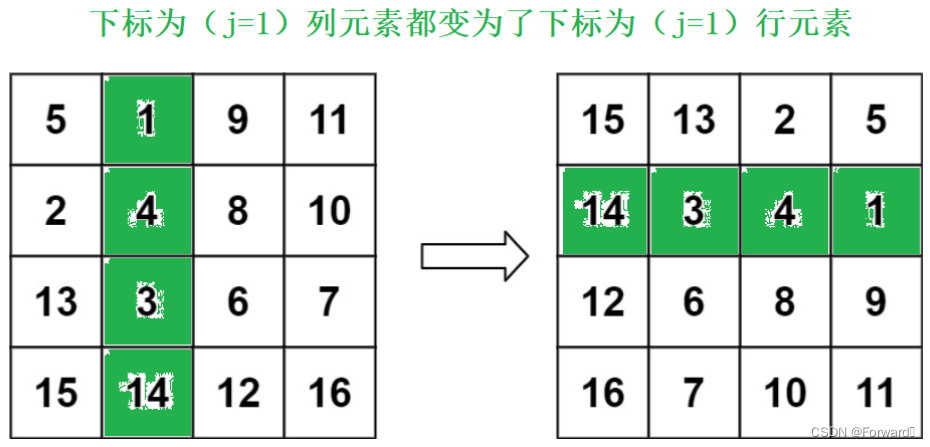
- 对于原数组的下标为
j列元素,顺时针旋转九十度后,都变成了下标为(j)行元素。如图所示:
- 结论:
假设带旋转的元素位置为
nums[i][j],那么顺时针旋转九十度后这个元素的位置就应该是nums[j][n-1-i]
这样想清楚后这题似乎就变得十分简单,但是我们应该想到旋转玩一组数据后,有些数据就会被覆盖,如图:

因此,我们可以再新创建一个临时数组来保存这些旋转后的数据,然后再将新数组的数据覆盖到原数组就可以了。
实现代码
void rotate(int** matrix, int matrixSize, int* matrixColSize){int n = matrixSize;//创建临时数组int **ret = (int**)malloc(sizeof(int*) * (n));for (int i = 0; i < n; i++)ret[i] = (int*)malloc(sizeof(int) * n);//先储存旋转后数组的数据for (int i = 0; i < n; i++)for (int j = 0; j < n; j++)ret[j][n - 1 - i] = matrix[i][j];//实现覆盖for (int i = 0; i < n; i++)for (int j = 0; j < n; j++)matrix[i][j] = ret[i][j];//释放临时数组的空间free(ret);
}
方法二: 原地旋转
我们先来看2 * 2数组顺时针旋转九十度的情形:

我们可以认为旋转过程是这样的:D->A、C->D、B->C、A->B,应该注意执行完D->A后,数据A就被覆盖了,因此我们需要创建一个临时变量来保存数据A,这样,这个旋转过程就变为了temp=A, D->A、C->D、B->C、temp->B

我们将数组扩大,那么由上面的推理可以得到,每经过上面的一轮变换,都可以旋转数组的4个元素:

那么如何将整个数组的元素都旋转,我们只需要取数组左上角1/4的元素,并将这些数据作为旋转起点,依次进行旋转即可:

同时经过分析我们也可以得到,一轮旋转的4个元素的下标变化应该是这样的:

最后,我们应该注意区分n为奇数或偶数的情况:
- 当n为偶数,数组的旋转起始位置(左上角1/4区域)为:

- 当n为奇数,数组的旋转起始位置(左上角1/4区域)为:

因此,当n为奇数或者偶数时,区域的列数都为n/2。当n为偶数时,行数为n/2,n为奇数时,行数为(n+1)/2
实现代码
void rotate(int** matrix, int matrixSize, int* matrixColSize){int n = matrixSize;//确定左上角1/4区域的范围int row = n / 2;int col = (n + 1) / 2;//以左上角1/4区域的每个元素为起点,依次进行旋转for (int i = 0; i < row; i++){for (int j = 0; j < col; j++){int temp = matrix[i][j];matrix[i][j] = matrix[n-1-j][i];matrix[n-1-j][i] = matrix[n-1-i][n-1-j];matrix[n-1-i][n-1-j] = matrix[j][n-1-i];matrix[j][n-1-i] = temp;}}
}
相关文章:

每日一题——旋转图像
旋转图像 题目链接 方法一:利用辅助数组 通过对示例的观察和分析,我们可以得到这样的结论: 对于原数组的下标为i行元素,顺时针旋转九十度后,都变成了下标为(n-1-i)列元素。如图所示ÿ…...

「Docker」《入门Docker:解放部署烦恼,提高开发效率》
《入门Docker:解放部署烦恼,提高开发效率》 一、引言1.1 Docker的定义和概念1.2 Docker的优势和应用场景 二、Docker基础知识2.1 Docker架构和组件2.2 Docker镜像和容器的关系2.3 Docker仓库和镜像的管理 三、安装和配置Docker环境3.1 安装Docker引擎3.2…...
)
数据结构--5.3图的遍历(广度优先遍历)
广度优先遍历: 广度优先遍历(BreadthFirstSearch),又称为广度优先搜索,简称BFS。 要实现对图的广度遍历,我们可以利用队列来实现。 void BFSTraverse(MGraph G) {int i,j;Queue Q;for(i0;i<G.numVerte…...
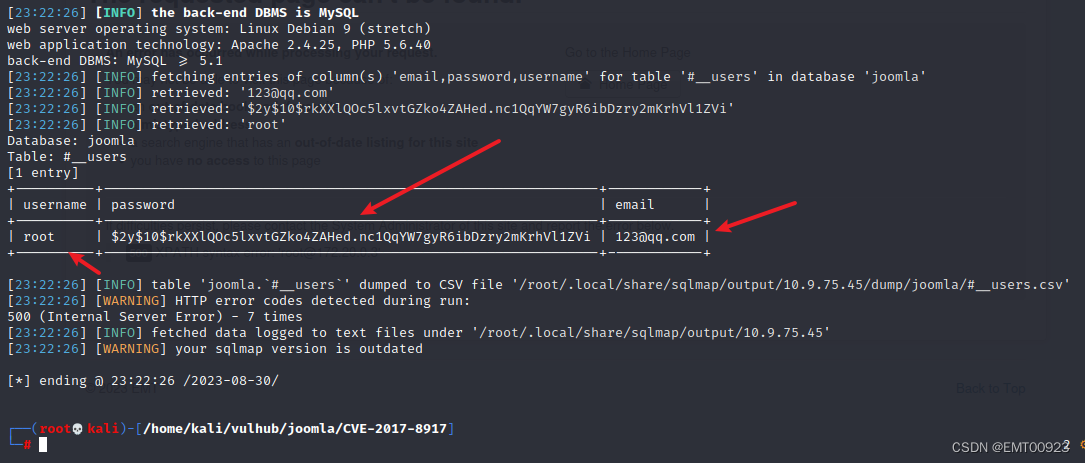
SQL注入漏洞复现(CVE-2017-8917)
文章目录 搭建环境启动环境漏洞复现报错注入使用sqlmap 前提条件: 1.安装docker docker pull medicean/vulapps:j_joomla_22.安装docker-compose docker run -d -p 8000:80 medicean/vulapps:j_joomla_23.下载vulhub Docker Compose是 docker 提供的一个命令行工具&…...
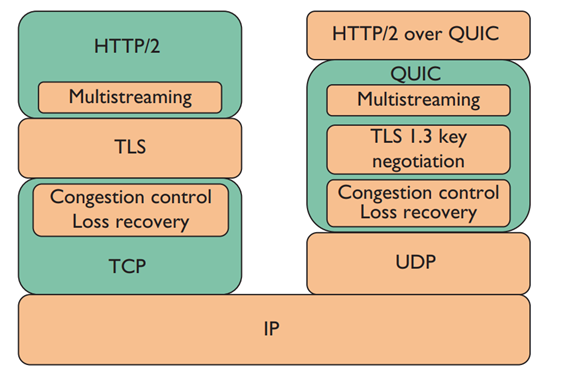
Http 1.0 1.1 2.0 3.0 版本差别
Http 1.0 发布年份:1996 非官方标准 短链接:每一次请求都对应一次TCP的连接与释放 开销大:每次请求都要TCP的连接与释放队头阻塞:每次请求都必须等上一次请求获得响应之后,才可以发送;效率低下 缓存&…...

javaee spring 依赖注入之复杂类型的注入数组 集合 等
spring 依赖注入之复杂类型的注入 package com.test.pojo;import java.util.List; import java.util.Map; import java.util.Properties;/*** description:* projectName:testSpring* see:com.test.pojo* createTime:2023/8/27 14:39*/ public class AA {private int[] arr;pr…...
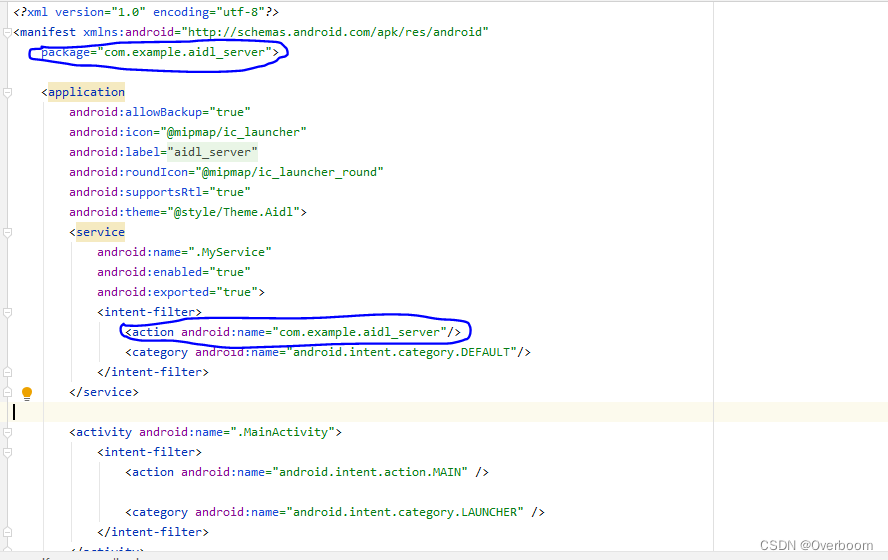
[Android AIDL] --- AIDL工程搭建
0 AIDL概念 AIDL(Android Interface Definition Language)是一种 IDL 语言,用于生成可以在 Android 设备上两个进程之间进行进程间通信(IPC)的代码。 通过 AIDL,可以在一个进程中获取另一个进程的数据和调…...

正中优配:回购!回购!再回购!已成A股新常态?
上市公司回购潮还在继续! 8月30日,海通证券、捷佳伟创等多家上市公司纷繁发布回购公告。自8月18日证监会提出“放宽相关回购条件,支撑上市公司展开股份回购”以来,A股上市公司掀起了一轮“回购潮”。Wind数据显现,8月…...
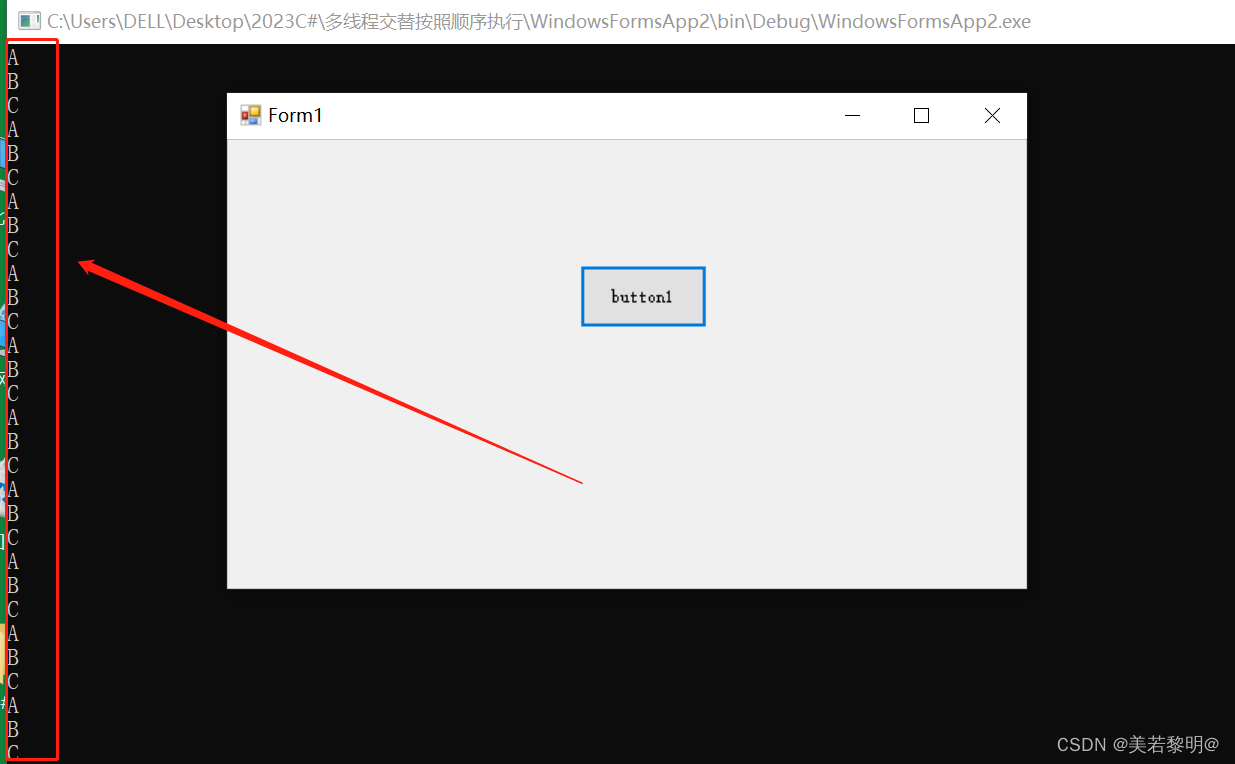
C# 多线程交替按照指定顺序执行
1.关于AutoResetEvent和ManualResetEvent的区别解释如下: AutoResetEvent和ManualResetEvent是.NET中的两个线程同步类。它们之间的主要区别在于其释放信号的方式以及对等待线程的影响。 AutoResetEvent的作用是在等待的线程被信号唤醒后,将信号自动重…...
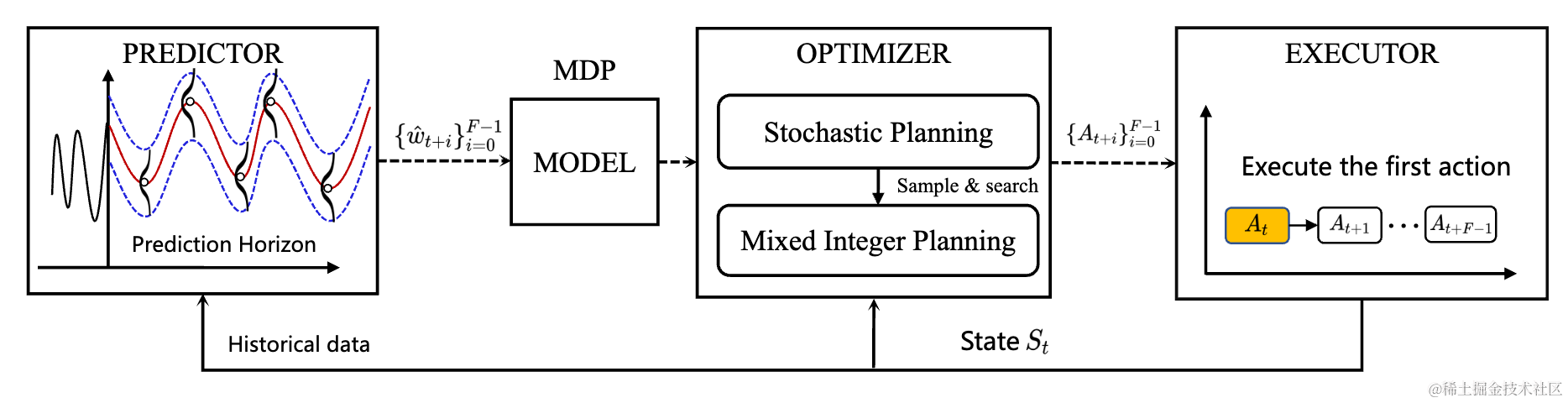
【VLDB 2023】基于预测的云资源弹性伸缩框架MagicScaler,实现“高QoS,低成本”双丰收
开篇 近日,由阿里云计算平台大数据基础工程技术团队主导,与计算平台MaxCompute团队、华东师范大学数据科学与工程学院、达摩院合作,基于预测的云计算平台资源弹性伸缩框架论文《MagicScaler: Uncertainty-aware, Predictive Autoscaling 》被…...
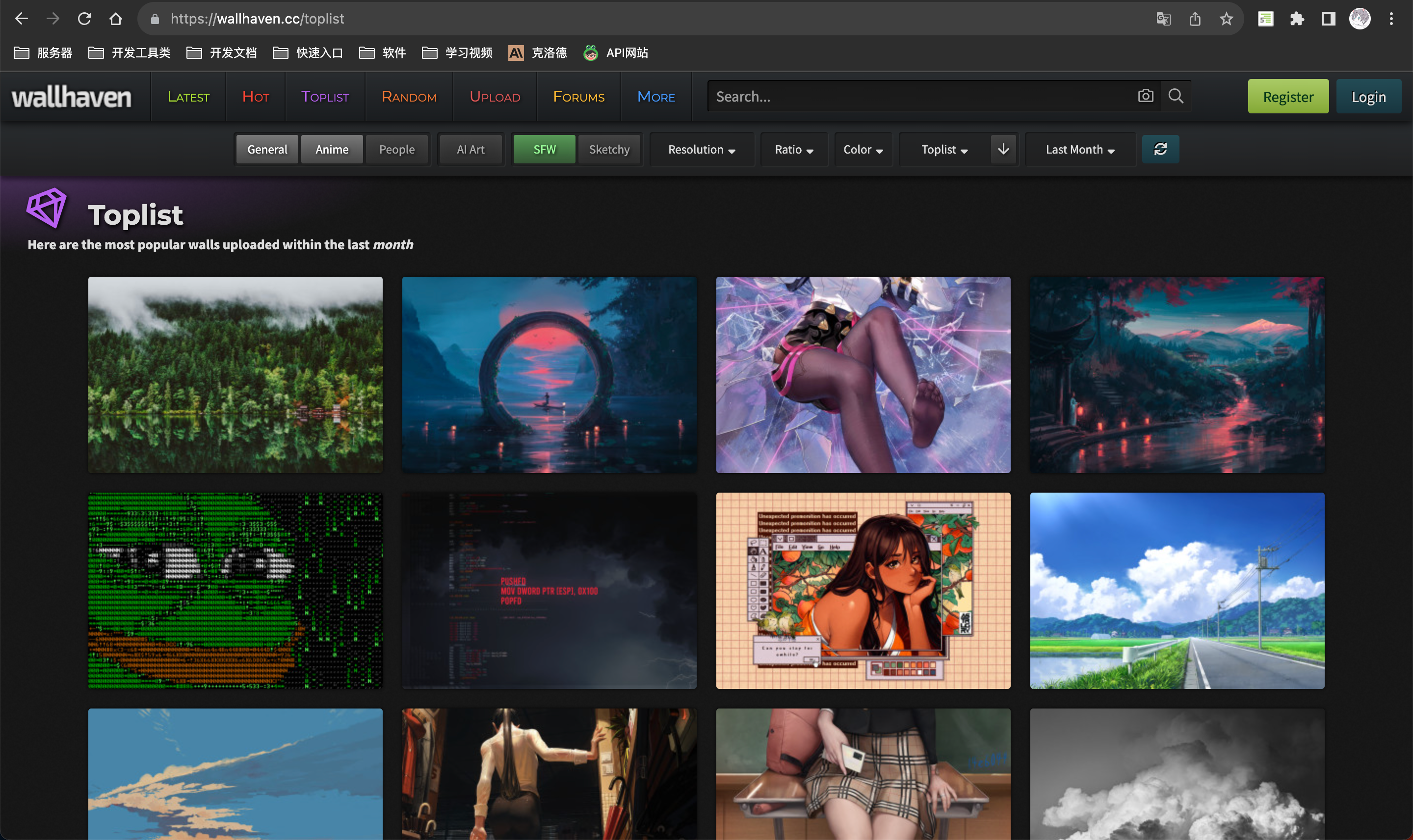
Node爬虫项目精简版 wallhaven网站实操 2023.8.29
练习地址: https://wallhaven.cc/toplist const express require(express); const axios require(axios); const cheerio require(cheerio); const schedule require(node-schedule); const fs require(fs);async function downloadImage(url) {const response…...

Vue统计图表的数据标签和数值显示技巧
Vue统计图表的数据标签和数值显示技巧 在开发Web应用程序时,统计图表是非常重要的数据呈现方式。Vue是一种流行的JavaScript框架,它提供了许多方便的功能来处理和展示数据。在这篇文章中,我们将探讨如何使用Vue来添加数据标签和数值显示到统…...

Linux 虚拟机同步时间crontab以及crond详解
目录 一 Linux 虚拟机同步时间设置 1. 检查是否安装cron服务(即时间同步器) 2. 下载时间同步器 3. 编辑crontab 内容 4. 同步更新电脑网络时间 5.设置 reload 6. 查看 crond 状态 二 crond 详解 1. 启动/关闭cron服务 2. crontab命令格式 3. …...
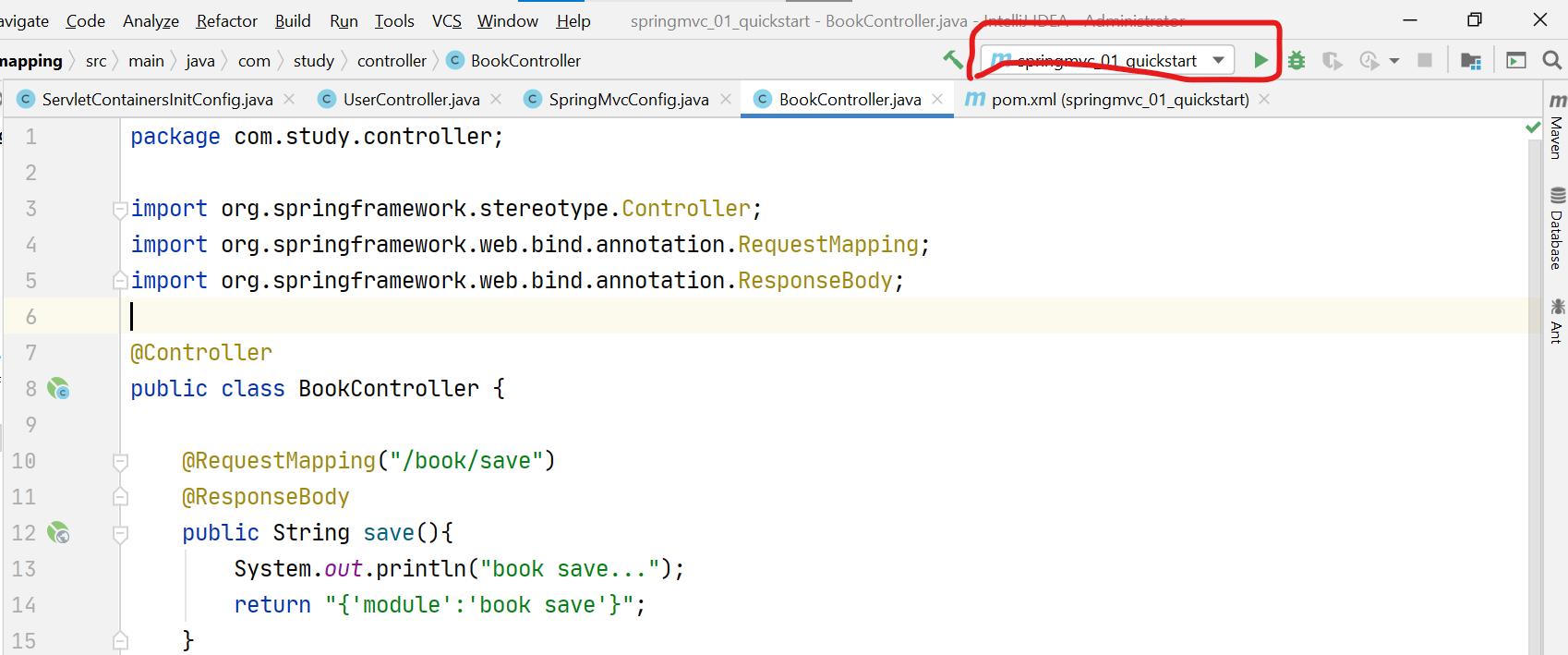
springmvc没有绿标,怎么配置tomcat插件运行?
一、添加插件后,刷新,自动从maven仓库下载tomcat插件 二、写好项目后,添加tomcat配置 三、即可点击绿标运行...

设计模式--模板方法模式(Template Method Pattern)
一、什么是模板方法模式(Template Method Pattern) 模板方法模式(Template Method Pattern)是一种行为型设计模式,它定义了一个算法的骨架,将一些步骤的实现延迟到子类中。模板方法模式允许在不改变算法的…...

linux 权限管理命令
权限管理命令 权限的查看及含义 可以使用ls -l来查看每个文件或目录的权限,一共有十位 ls -ls--------------------------------------------------------------------rw-------. 1 root root 946 Feb 14 16:13 anaconda-ks.cfgdrwxr-xr-x. 2 root root 4096 Feb…...
c++ qt--线程(一)(第八部分)
c qt–线程(一)(第八部分) 一.进程(Process) 在任务管理器中的进程页下,可以看到进程,任务管理器将进程分为了三类,应用、后台进程、window进程 应用: 打开…...

参数初始化方法
梯度消失与梯度爆炸 考虑一个 3 层的全连接网络。 H 1 X W 1 H{1}X \times W{1} H1XW1, H 2 H 1 W 2 H{2}H{1} \times W{2} H2H1W2, O u t H 2 W 3 OutH{2} \times W_{3} OutH2W3 其中第 2 层的权重梯度如下: Δ W 2 ∂ L o s s …...
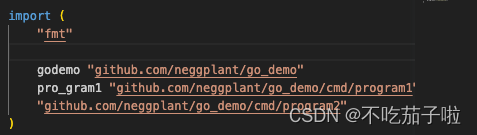
Go的基础运行方式和打包
目录 基础运行方式导入路径 打包技巧相关知识点 基础运行方式 // 文件名可以不是main,但包名和入口函数比如是main // main.go package main // 导入包的时候可以直接导入,也可以导入后指定包名, import ("fmt"godemo "githu…...

Deepin 图形化部署 Hadoop Single Node Cluster
Deepin 图形化部署 Hadoop Single Node Cluster 升级操作系统和软件 快捷键 ctrlaltt 打开控制台窗口 更新 apt 源 sudo apt update更新 系统和软件 sudo apt -y dist-upgrade升级后建议重启 开启ssh服务 打开资源管理器 进入系统盘 找到 etc 目录 在系统盘的 etc 目录上 右键…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...
