参数初始化方法
梯度消失与梯度爆炸
考虑一个 3 层的全连接网络。
H 1 = X × W 1 H{1}=X \times W{1} H1=X×W1, H 2 = H 1 × W 2 H{2}=H{1} \times W{2} H2=H1×W2, O u t = H 2 × W 3 Out=H{2} \times W_{3} Out=H2×W3
其中第 2 层的权重梯度如下:
Δ W 2 = ∂ L o s s ∂ W 2 = ∂ L o s s ∂ o u t ∂ o u t ∂ H 2 ∂ H 2 ∂ w 2 = ∂ L o s s ∂ o u t ∂ o u t ∂ H 2 H 1 \begin{aligned} \Delta \mathrm{W}{2} &=\frac{\partial \mathrm{Loss}}{\partial \mathrm{W}{2}}=\frac{\partial \mathrm{Loss}}{\partial \mathrm{out}} \frac{\partial \mathrm{out}}{\partial \mathrm{H}_{2}} \frac{\partial \mathrm{H}{2}}{\partial \mathrm{w}{2}} \ &=\frac{\partial \mathrm{Loss}}{\partial \mathrm{out}} \frac{\partial \mathrm{out}}{\partial \mathrm{H}_{2}} \mathrm{H}_{1} \end{aligned} ΔW2=∂W2∂Loss=∂out∂Loss∂H2∂out∂w2∂H2 =∂out∂Loss∂H2∂outH1
所以 Δ W 2 \Delta \mathrm{W}{2} ΔW2依赖于前一层的输出 H 1 H{1} H1。如果 H 1 H{1} H1 趋近于零,那么 Δ W 2 \Delta \mathrm{W}{2} ΔW2也接近于 0,造成梯度消失。如果 H 1 H{1} H1 趋近于无穷大,那么 Δ W 2 \Delta \mathrm{W}{2} ΔW2也接近于无穷大,造成梯度爆炸。要避免梯度爆炸或者梯度消失,就要严格控制网络层输出的数值范围。
下面构建 100 层全连接网络,先不适用非线性激活函数,每层的权重初始化为服从 N ( 0 , 1 ) N(0,1) N(0,1)的正态分布,输出数据使用随机初始化的数据。
import torch
import torch.nn as nn
from common_tools import set_seedset_seed(1) # 设置随机种子class MLP(nn.Module):def __init__(self, neural_num, layers):super(MLP, self).__init__()self.linears = nn.ModuleList([nn.Linear(neural_num, neural_num, bias=False) for i in range(layers)])self.neural_num = neural_numdef forward(self, x):for (i, linear) in enumerate(self.linears):x = linear(x)return xdef initialize(self):for m in self.modules():# 判断这一层是否为线性层,如果为线性层则初始化权值if isinstance(m, nn.Linear):nn.init.normal_(m.weight.data) # normal: mean=0, std=1layer_nums = 100
neural_nums = 256
batch_size = 16net = MLP(neural_nums, layer_nums)
net.initialize()inputs = torch.randn((batch_size, neural_nums)) # normal: mean=0, std=1output = net(inputs)
print(output)
输出为:
tensor([[nan, nan, nan, ..., nan, nan, nan],[nan, nan, nan, ..., nan, nan, nan],[nan, nan, nan, ..., nan, nan, nan],...,[nan, nan, nan, ..., nan, nan, nan],[nan, nan, nan, ..., nan, nan, nan],[nan, nan, nan, ..., nan, nan, nan]], grad_fn=<MmBackward>)
也就是数据太大(梯度爆炸)或者太小(梯度消失)了。接下来我们在forward()函数中判断每一次前向传播的输出的标准差是否为 nan,如果是 nan 则停止前向传播。
def forward(self, x):for (i, linear) in enumerate(self.linears):x = linear(x)print("layer:{}, std:{}".format(i, x.std()))if torch.isnan(x.std()):print("output is nan in {} layers".format(i))breakreturn x
输出如下:
layer:0, std:15.959932327270508
layer:1, std:256.6237487792969
layer:2, std:4107.24560546875
.
.
.
layer:29, std:1.322983152787379e+36
layer:30, std:2.0786820453988485e+37
layer:31, std:nan
output is nan in 31 layers
可以看到每一层的标准差是越来越大的,并在在 31 层时超出了数据可以表示的范围。
下面推导为什么网络层输出的标准差越来越大。
首先给出 3 个公式:
E ( X × Y ) = E ( X ) × E ( Y ) E(X \times Y)=E(X) \times E(Y) E(X×Y)=E(X)×E(Y):两个相互独立的随机变量的乘积的期望等于它们的期望的乘积。
D ( X ) = E ( X 2 ) − [ E ( X ) ] 2 D(X)=E(X^{2}) - [E(X)]^{2} D(X)=E(X2)−[E(X)]2:一个随机变量的方差等于它的平方的期望减去期望的平方
D ( X + Y ) = D ( X ) + D ( Y ) D(X+Y)=D(X)+D(Y) D(X+Y)=D(X)+D(Y):两个相互独立的随机变量之和的方差等于它们的方差的和。
可以推导出两个随机变量的乘积的方差如下:
D ( X × Y ) = E [ ( X Y ) 2 ] − [ E ( X Y ) ] 2 = D ( X ) × D ( Y ) + D ( X ) × [ E ( Y ) ] 2 + D ( Y ) × [ E ( X ) ] 2 D(X \times Y)=E[(XY)^{2}] - [E(XY)]^{2}=D(X) \times D(Y) + D(X) \times [E(Y)]^{2} + D(Y) \times [E(X)]^{2} D(X×Y)=E[(XY)2]−[E(XY)]2=D(X)×D(Y)+D(X)×[E(Y)]2+D(Y)×[E(X)]2
如果 E ( X ) = 0 E(X)=0 E(X)=0, E ( Y ) = 0 E(Y)=0 E(Y)=0,那么 D ( X × Y ) = D ( X ) × D ( Y ) D(X \times Y)=D(X) \times D(Y) D(X×Y)=D(X)×D(Y)
我们以输入层第一个神经元为例:
H 11 = ∑ i = 0 n X i × W 1 i \mathrm{H}_{11}=\sum{i=0}^{n} X{i} \times W{1 i} H11=∑i=0nXi×W1i
其中输入 X 和权值 W 都是服从 N ( 0 , 1 ) N(0,1) N(0,1)的正态分布,所以这个神经元的方差为:
D ( H 11 ) = ∑ i = 0 n D ( X i ) ∗ D ( W 1 i ) = n ( 1 ∗ 1 ) = n \begin{aligned} \mathbf{D}\left(\mathrm{H}_{11}\right) &=\sum{i=0}^{n} \boldsymbol{D}\left(X{i}\right) * \boldsymbol{D}\left(W{1 i}\right) \ &=n (1 * 1) \ &=n \end{aligned} D(H11)=∑i=0nD(Xi)∗D(W1i) =n(1∗1) =n
标准差为: std ( H 11 ) = D ( H 11 ) = n \operatorname{std}\left(\mathrm{H}_{11}\right)=\sqrt{\mathbf{D}\left(\mathrm{H}_{11}\right)}=\sqrt{n} std(H11)=D(H11)=n,所以每经过一个网络层,方差就会扩大 n 倍,标准差就会扩大 n \sqrt{n} n倍,n 为每层神经元个数,直到超出数值表示范围。对比上面的代码可以看到,每层神经元个数为 256,输出数据的标准差为 1,所以第一个网络层输出的标准差为 16 左右,第二个网络层输出的标准差为 256 左右,以此类推,直到 31 层超出数据表示范围。可以把每层神经元个数改为 400,那么每层标准差扩大 20 倍左右。从 D ( H 11 ) = ∑ i = 0 n D ( X i ) × D ( W 1 i ) D(\mathrm{H}_{11})=\sum{i=0}^{n} D(X{i}) \times D(W{1 i}) D(H11)=∑i=0nD(Xi)×D(W1i),可以看出,每一层网络输出的方差与神经元个数、输入数据的方差、权值方差有关,其中比较好改变的是权值的方差 D ( W ) D(W) D(W),所以 D ( W ) = 1 n D(W)= \frac{1}{n} D(W)=n1,标准差为 s t d ( W ) = 1 n std(W)=\sqrt\frac{1}{n} std(W)=n1。
因此修改权值初始化代码为nn.init.normal_(m.weight.data, std=np.sqrt(1/self.neural_num)),
结果如下:
layer:0, std:0.9974957704544067
layer:1, std:1.0024365186691284
layer:2, std:1.002745509147644
.
.
.
layer:94, std:1.031973123550415
layer:95, std:1.0413124561309814
layer:96, std:1.0817031860351562
修改之后,没有出现梯度消失或者梯度爆炸的情况,每层神经元输出的方差均在 1 左右。通过恰当的权值初始化,可以保持权值在更新过程中维持在一定范围之内,不过过大,也不会过小。
上述是没有使用非线性变换的实验结果,如果在forward()中添加非线性变换tanh,每一层的输出方差还是会越来越小,会导致梯度消失。因此出现了 Xavier 初始化方法与 Kaiming 初始化方法。
Xavier 方法
Xavier 是 2010 年提出的,针对有非线性激活函数时的权值初始化方法,目标是保持数据的方差维持在 1 左右,主要针对饱和激活函数如 sigmoid 和 tanh 等。同时考虑前向传播和反向传播,需要满足两个等式: n i ∗ D ( W ) = 1 \boldsymbol{n}_{\boldsymbol{i}} * \boldsymbol{D}(\boldsymbol{W})=\mathbf{1} ni∗D(W)=1和 n i + 1 ∗ D ( W ) = 1 \boldsymbol{n}_{\boldsymbol{i+1}} * \boldsymbol{D}(\boldsymbol{W})=\mathbf{1} ni+1∗D(W)=1,可得: D ( W ) = 2 n i + n i + 1 D(W)=\frac{2}{n_{i}+n_{i+1}} D(W)=ni+ni+12。为了使 Xavier 方法初始化的权值服从均匀分布,假设 W W W服从均匀分布 U [ − a , a ] U[-a, a] U[−a,a],那么方差 D ( W ) = ( − a − a ) 2 12 = ( 2 a ) 2 12 = a 2 3 D(W)=\frac{(-a-a)^{2}}{12}=\frac{(2 a)^{2}}{12}=\frac{a^{2}}{3} D(W)=12(−a−a)2=12(2a)2=3a2,令 2 n i + n i + 1 = a 2 3 \frac{2}{n_{i}+n_{i+1}}=\frac{a^{2}}{3} ni+ni+12=3a2,解得: a = 6 n i + n i + 1 \boldsymbol{a}=\frac{\sqrt{6}}{\sqrt{n_{i}+n_{i+1}}} a=ni+ni+16,所以 W W W服从分布 U [ − 6 n i + n i + 1 , 6 n i + n i + 1 ] U\left[-\frac{\sqrt{6}}{\sqrt{n_{i}+n_{i+1}}}, \frac{\sqrt{6}}{\sqrt{n_{i}+n_{i+1}}}\right] U[−ni+ni+16,ni+ni+16]
所以初始化方法改为:
a = np.sqrt(6 / (self.neural_num + self.neural_num))
# 把 a 变换到 tanh,计算增益
tanh_gain = nn.init.calculate_gain('tanh')
a *= tanh_gainnn.init.uniform_(m.weight.data, -a, a)
并且每一层的激活函数都使用 tanh,输出如下:
layer:0, std:0.7571136355400085
layer:1, std:0.6924336552619934
layer:2, std:0.6677976846694946
.
.
.
layer:97, std:0.6426210403442383
layer:98, std:0.6407480835914612
layer:99, std:0.6442216038703918
可以看到每层输出的方差都维持在 0.6 左右。
PyTorch 也提供了 Xavier 初始化方法,可以直接调用:
tanh_gain = nn.init.calculate_gain('tanh')
nn.init.xavier_uniform_(m.weight.data, gain=tanh_gain)
- nonlinearity:激活函数名称
- param:激活函数的参数,如 Leaky ReLU 的 negative_slop。下面是计算标准差经过激活函数的变化尺度的代码。
x = torch.randn(10000)
out = torch.tanh(x)
gain = x.std() / out.std()
print('gain:{}'.format(gain))
tanh_gain = nn.init.calculate_gain('tanh')
print('tanh_gain in PyTorch:', tanh_gain)
输出如下:
gain:1.5982500314712524
tanh_gain in PyTorch: 1.6666666666666667
结果表示,原有数据分布的方差经过 tanh 之后,标准差会变小 1.6倍左右。
Kaiming 方法
虽然 Xavier 方法提出了针对饱和激活函数的权值初始化方法,但是 AlexNet 出现后,大量网络开始使用非饱和的激活函数如 ReLU 等,这时 Xavier 方法不再适用。2015 年针对 ReLU 及其变种等激活函数提出了 Kaiming 初始化方法。
针对 ReLU,方差应该满足: D ( W ) = 2 n i \mathrm{D}(W)=\frac{2}{n_{i}} D(W)=ni2;针对 ReLu 的变种,方差应该满足: D ( W ) = 2 n i \mathrm{D}(W)=\frac{2}{n_{i}} D(W)=ni2,a 表示负半轴的斜率,如 PReLU 方法,标准差满足 std ( W ) = 2 ( 1 + a 2 ) ∗ n i \operatorname{std}(W)=\sqrt{\frac{2}{\left(1+a^{2}\right) * n_{i}}} std(W)=(1+a2)∗ni2。
代码如下:nn.init.normal(m.weight.data, std=np.sqrt(2 / self.neuralnum)),或者使用 PyTorch 提供的初始化方法:nn.init.kaiming_normal(m.weight.data),同时把激活函数改为 ReLU。
常用初始化方法
PyTorch 中提供了 10 中初始化方法
- Xavier 均匀分布
- Xavier 正态分布
- Kaiming 均匀分布
- Kaiming 正态分布
- 均匀分布
- 正态分布
- 常数分布
- 正交矩阵初始化
- 单位矩阵初始化
- 稀疏矩阵初始化
每种初始化方法都有它自己使用的场景,原则是保持每一层输出的方差不能太大,也不能太小。
相关文章:

参数初始化方法
梯度消失与梯度爆炸 考虑一个 3 层的全连接网络。 H 1 X W 1 H{1}X \times W{1} H1XW1, H 2 H 1 W 2 H{2}H{1} \times W{2} H2H1W2, O u t H 2 W 3 OutH{2} \times W_{3} OutH2W3 其中第 2 层的权重梯度如下: Δ W 2 ∂ L o s s …...
Go的基础运行方式和打包
目录 基础运行方式导入路径 打包技巧相关知识点 基础运行方式 // 文件名可以不是main,但包名和入口函数比如是main // main.go package main // 导入包的时候可以直接导入,也可以导入后指定包名, import ("fmt"godemo "githu…...

Deepin 图形化部署 Hadoop Single Node Cluster
Deepin 图形化部署 Hadoop Single Node Cluster 升级操作系统和软件 快捷键 ctrlaltt 打开控制台窗口 更新 apt 源 sudo apt update更新 系统和软件 sudo apt -y dist-upgrade升级后建议重启 开启ssh服务 打开资源管理器 进入系统盘 找到 etc 目录 在系统盘的 etc 目录上 右键…...

23款奔驰GLS400升级柏林之声音响系统,体验不一样的感觉
Burmester 环绕立体声音响系统–为每位乘员打造令人印象深刻的音质13个高性能扬声器、总功率为590瓦的9声道数字信号处理器(DSP)放大器以及放大器/扬声器系统专为车辆配置,打造出一流的Burmester之音。必要时还可进一步提升令人印象深刻的听觉体验。声音环绕功能能够…...
方法和filter()方法的使用)
Vue的map()方法和filter()方法的使用
map() map():方法返回一个新数组,数组中的元素为原始数组元素调用函数处理后的值 案例: const data res.map(item > item.id); const data res.map(item > return item.id); const data res.map(item > { name: item.name, id…...

qt创建临时文件
1、临时文件系统 在 Linux 系统中,创建临时文件系统很简单,执行如下指令即可: mount -t tmpfs -o size1024m tmpfs /mnt/tmp 挂载成功后,在 /mnt/tmp 这个挂载点下创建的所有文件都将会是临时文件, 也就是说:当电脑关…...

Element——table排序,上移下移功能。及按钮上一条下一条功能
需求:table排序,可操作排序上移下移功能。判断第一行上移禁用和最后一行下移禁用,排序根据后端返回的字段 <el-table:data"tableData"style"width: 100%"><el-table-column type"index" label"序…...

无涯教程-Android - Linear Layout函数
Android LinearLayout是一个视图组,该视图组将垂直或水平的所有子级对齐。 Linear Layout - 属性 以下是LinearLayout特有的重要属性- Sr.NoAttribute & 描述1 android:id 这是唯一标识布局的ID。 2 android:baselineAligned 此值必须是布尔值,为…...
ELK安装、部署、调试(六) logstash的安装和配置
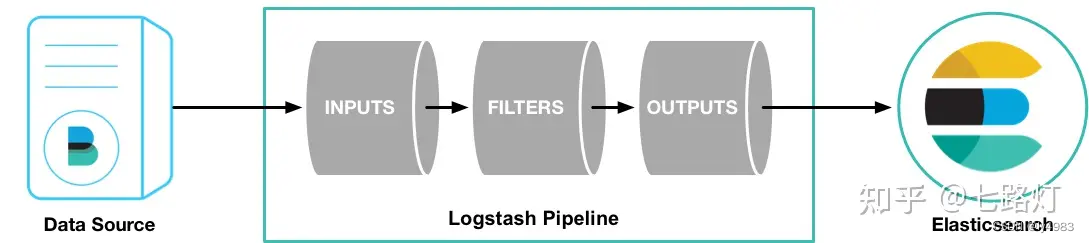
1.介绍 Logstash是具有实时流水线能力的开源的数据收集引擎。Logstash可以动态统一不同来源的数据,并将数据标准化到您选择的目标输出。它提供了大量插件,可帮助我们解析,丰富,转换和缓冲任何类型的数据。 管道(Logs…...

【Spring Security】UserDetails 接口介绍
文章目录 UserDetails 的作用UserDetails 接口中各个方法详解 UserDetails 的作用 UserDetails 在 Spring Security 框架中主要担任获取用户信息的接口,通过该接口就能拿到用户的信息和验证用户的信息,这些信息在下面的方法中会有讲述。 UserDetails 接…...
C# Linq源码分析之Take(四)
概要 本文主要对Take的优化方法进行源码分析,分析Take在配合Select,Where等常用的Linq扩展方法使用时候,如何实现优化处理。 本文涉及到Select, Where和Take和三个方法的源码分析,其中Select, Where, Take更详尽的源码分析&…...

Python 和 C++ 使用细节差别
1. 循环中的可迭代对象长度 1. 循环中的可迭代对象长度 C 中,for循环中写明a.size(),每次循环这个值是重新计算的; # include “iostream” # include <vector> using namespace std;int main() {vector<int> a(10);int cnt 0…...
在Ubuntu Linux系统上安装RabbitMQ服务并解决公网远程访问问题
文章目录 前言1.安装erlang 语言2.安装rabbitMQ3. 内网穿透3.1 安装cpolar内网穿透(支持一键自动安装脚本)3.2 创建HTTP隧道 4. 公网远程连接5.固定公网TCP地址5.1 保留一个固定的公网TCP端口地址5.2 配置固定公网TCP端口地址 前言 RabbitMQ是一个在 AMQP(高级消息队列协议)基…...
葫芦娃自动预约-公众号代挂
效果 #小程序://航旅黔购/1nkYlNRVzm0Gg9x #小程序://贵旅优品/7zz6mtnSVgDfyqa #小程序://新联惠购/ibFdsuhWqIbczEd #小程序://贵盐黔品/u2TgExCUdkavrFe #小程序://空港乐购/ANkOOdqEeo71kah #小程序://遵航出山/ZkR7DQy1raoPxKD #小程序://乐旅商城/Ip5cgpJ7TLmRrWF #小程序…...
ESP32应用教程(0)— PMW3901MB光流传感器
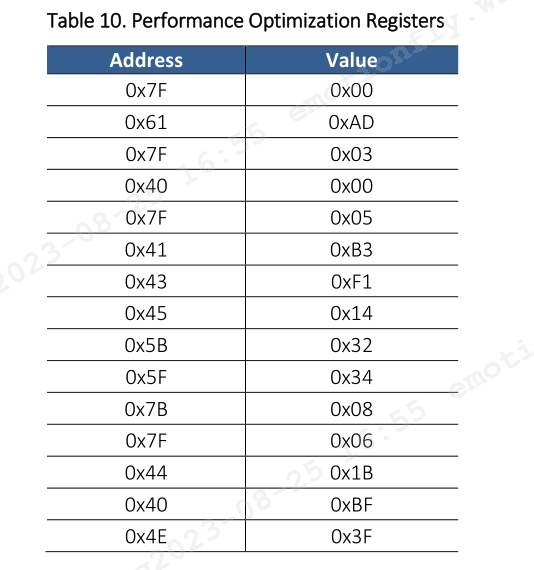
文章目录 前言 1 传感器介绍 1.1 关键特征 1.2 关键参数 2 硬件概述 2.1 信号引脚 2.2 参考电路图 3 寄存器 3.1 寄存器列表 3.2 性能优化寄存器 4 代码说明 4.1 结构体说明 4.2 编译说明 5 波形分析 前言 本文介绍了在 ESP32 DEVKIT V1 开发板上开发 PMW3901MB…...
docker部署nginx,部署springboot项目,并实现访问
一、先部署springboot项目 1、安装docker: yum install docker -y 2、启动docker: service docker start 重启: service docker restart 3、查看版本: docker -v 4、使设置docker.service生效(路径:…...

十五、模板方法模式
一、什么是模板方法模式 模板方法(Template Method)模式的定义如下:定义一个操作中的算法骨架,而将算法的一些步骤延迟到子类中,使得子类可以不改变该算法结构的情况下重定义该算法的某些特定步骤。 模板方法模式包含以…...
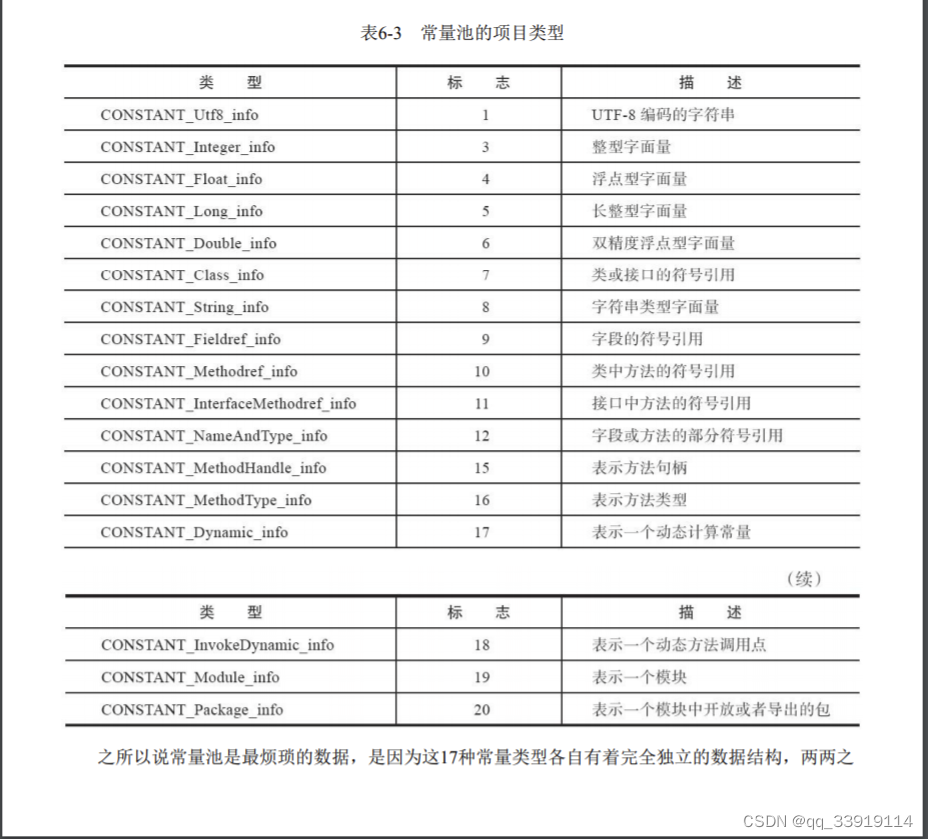
jvm 什么是常量池,常量池定义 class常量池
首先需要理解下Java的class文件,以及class文件结构: 1.Class文件是一组以8个字节为基础单位的二进制流,各个数据项目严格按照顺序紧凑地排列在文 件之中,中间没有任何分隔符,这使得整个Class文件中存储的内容几乎全部…...

CA证书颁发机构服务器
目录 一、CA证书颁发机构是什么? 二、数字证书可以干什么? 三、PKI:即公钥加密体系(public key cryptography) 四、CA在网络中的工作流程及原理(以网站为例) 五、HTTPS 的工作原理 六、CA私有证…...

5. 线性层及其他层
5.1 神经网络结构 5.2 线性拉平 import torch import torchvision from torch import nn from torch.nn import ReLU from torch.nn import Sigmoid from torch.utils.data import DataLoader from torch.utils.tensorboard import SummaryWriterdataset torchvision.datase…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

微服务通信安全:深入解析mTLS的原理与实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、引言:微服务时代的通信安全挑战 随着云原生和微服务架构的普及,服务间的通信安全成为系统设计的核心议题。传统的单体架构中&…...
