双因素方差分析全流程
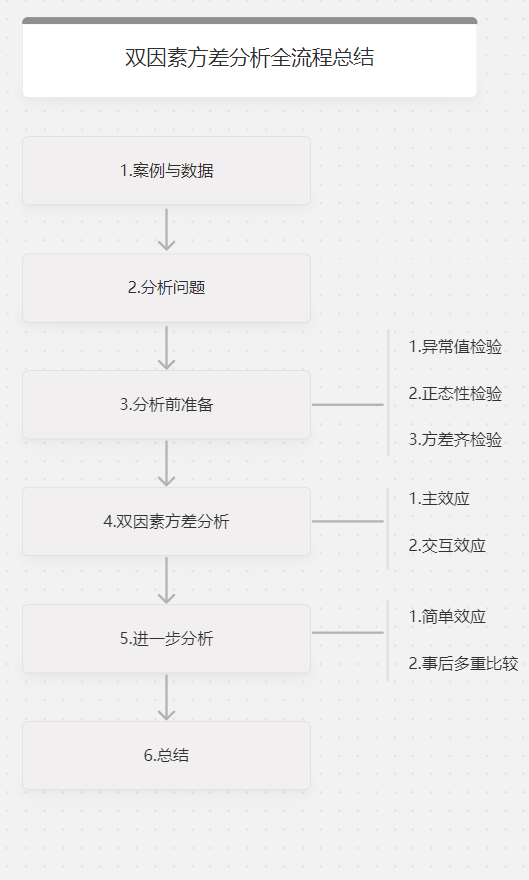
上篇文章讲述了“单因素方差分析全流程总结”,单因素方差分析只是考虑了一个自变量(定类)与一个因变量(定量)之间的关系,但是在实际问题研究中可能研究两个或者几个因素与因变量之间的关系,例如,分析产品满意度与学历、品牌满意度等的关系。当方差分析中研究几个自变量和1个因变量之间的关系时,称为多因素方差分析。如果是两个自变量则为双因素方差分析。
一、案例与数据
有四个品牌的吸尘器在两个地区的不同门店销售,为分析吸尘器的品牌和销售地区对销售量的影响,搜集每个品牌在各地区的销售数据,销售经理根据搜集的数据想要进行分析品牌和地区对吸尘器的销售量是否有显著差异以及两个因素搭配是否对销售量产生新的影响,部分数据如下:
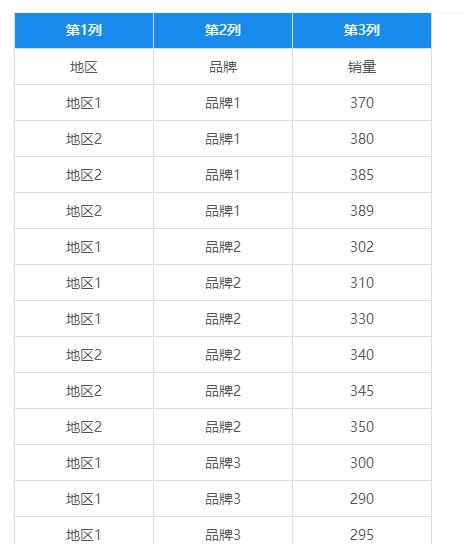
二、分析问题
例子中涉及三个变量,一个是“地区”一个是“品牌”还有一个是“销售量”。其中“地区”和“品牌”是定类变量,“销售量”是定量变量,想要进行分析品牌和地区对吸尘器的销售量是否有显著差异,分析究竟是一个因素在起作用,还是两个因素都在起作用,还是两个因素都不起作用。这就是一个双因素方差分析问题。
三、分析前准备
在进行双因素方差分析前需要进行分析前准备,首先进行数据的异常值检查,然后验证数据是否满足双因素方差分析的要求:
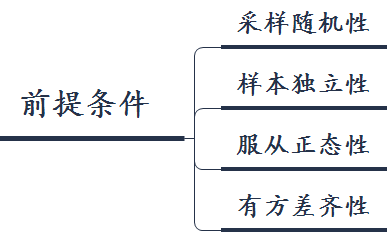
案例已经满足前两个条件,只需验证在个总体中,每个总体服从正态分布和方差齐性。
1、异常值检验
异常值是指在数据中不正常的值,也称离群值,比如大于三倍标准差等。与其它方差分析一致,双因素方差分析对异常值也比较敏感,这些数据可能会导致分析结果异常,比如扭曲各分类之间的差异,所以检验异常值尤为重要。利用SPSSAU箱线图进行查看直观且容易查看异常值点。
不同地区的销量:
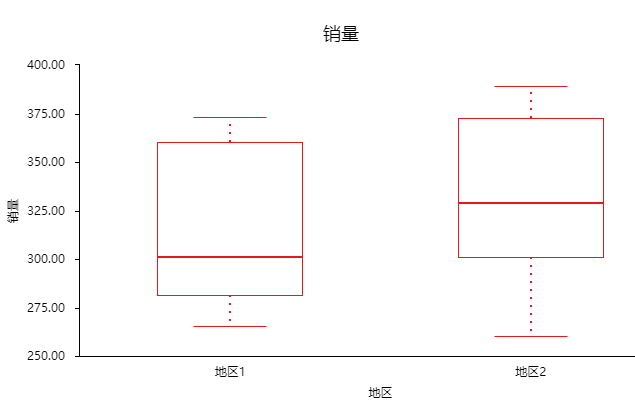
从箱线图中可以看出不同地区吸尘器的销量没有发现异常值。
不同品牌的销量:

从箱线图中可以看出不同品牌吸尘器的销量没有发现异常值。综上:数据中暂未发现异常值,不需要处理。
那么如果出现异常值如何处理呢?
常见做法是将异常值剔除,重新进行分析,有时异常值数量较多,不希望剔除,那么也可以处理为缺失值进行填补(一般平均值和中位数等使用较多),或者利用插值法进行插值。接下来进行检查数据是否符合方差分析的前提条件,首先进行正态性检验。
2、正态性检验
检验数据是否服从正态分布有很多种方式其中包括正态性检验以及图示化P-P图或者Q-Q图等,例子中要检验每个总体是否服从正态分布,由于正态性检验最为严谨,所以这里使用正态性检验进行分析。不同品牌的销量结果如下:
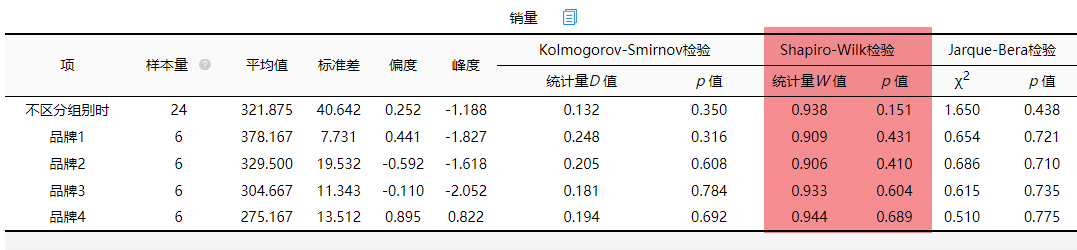
SPSSAU共提供三种正态性检验其中包括K-S检验(Kolmogorov-Smirnov检验)、S-W检验(Shapiro-Wilk检验)以及J-B检验(Jarque-Bera检验),由于每个个体的样本为6个总样本量为24个小于50所以为小样本分析,使用S-W检验进行分析即可,如果样本量较大(比如大于50)可以考虑使用K-S或者J-B检验。发现S-W检验中p值均大于0.05,所以不同地区的销量满足正态性检验,不同地区吸尘器的销量分析也是如此:

综上,每个总体服从正态分布,接下来验证是否服从方差齐性。
3、方差齐检验
方差齐性指自变量X的取值范围内,不论X取什么值,对应的Y为服从正态分布的随机变量,并具有相同的方差,即Y的方差与X值的大小无关(来源百度百科)。利用SPSSAU进行方差齐检验(分析路径【通用方法】→【方差】)。不同地区的销量方差齐分析如下:

利用方差齐性检验各组别数据的波动情况,从方差齐分析结果中可以看出结果的F值为0.043,p值为0.838大于0.05,说明不同地区的销量没有显著差异性,也即说明具有方差齐性,同理可以分析不同品牌的销量也具有方差齐性(不进行赘述)。

综上,每个总体服从方差齐性,并且满足双因素方差分析的前提条件,所以接下来进行双因素方差分析。
四、双因素方差分析
为了研究品牌和地区对吸尘器的销售量是否有显著差异以及两个因素搭配是否对销售量产生新的影响,以品牌和地区作为自变量,以销售量作为因变量进行双因素方差分析。
1、主效应
考虑某因素的主效应时,需要考虑除所有因素的效应,简单来说就是X对Y的影响。比如:双因素方差分析中,分别去判断“地区”和“品牌”对销售量的影响。
结果如下:
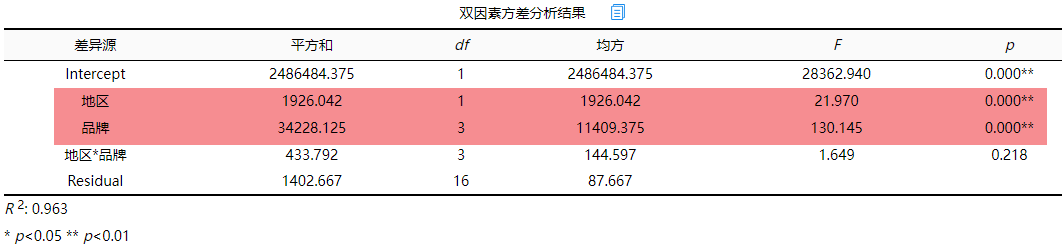
首先进行查看变量“地区”,发现自变量地区的F值为21.970,并且p值小于0.05所以说明主效应存在,然后对“品牌”进行分析,发现品牌的F值为130.145并且p值小于0.05所以说明主效应存在,具体差异可以进行事后多重比较进行分析。接下来研究“地区”和“品牌”搭配是否对销售量产生新的影响,进行查看交互效应。
2、交互效应
在双因素方差分析中,如果除了研究品牌和地区对销售量的影响还研究两个因素搭配是否对销售量产生新的影响,例如例子中的某个地区对某种品牌吸尘器有特殊偏好,则为双因素方差分析的交互作用分析,即交互效应。
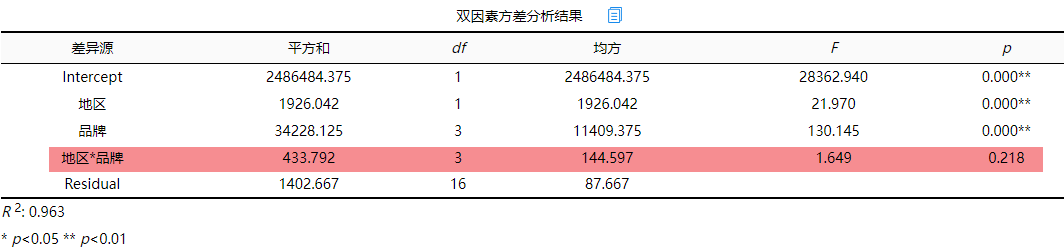
从上表可以看出,分析项为“地区与品牌的交互项”因变量为“销售量”发现模型的F值为1.649,并且p值为0.218大于0.05,所以模型不显著,即说明没有交互效应。分析完毕。综上,存在主效应但不存在交互效应,接下来进一步分析。
五、进一步分析
如果进行双因素方差分析,一般是主效应显著后才会进一步查看事后多重比较,对于交互作用显著的模型才会更深一步研究简单效应分析。
1、简单效应
简单效应是指简单效应指X1在某个水平时,X2不同水平的比较;因为该模型只存在主效应所以进行事后多重比较不进行简单效应分析。如果存在交互效应,则可以进一步分析简单效应。
2、事后多重比较
因为主效应显著,并且“地区”和“品牌”两个主效应都显著,所以进行事后多重比较,进一步分析(此处利用LSD方法进行,因为该方法对差异最为敏感使用最为广泛,并且检验效能高,对比组别较少时使用,除此之外SPSSAU还提供其它方法,比如:Bonferroni校正等)。
“地区”事后多重比较:

比较不同地区的销量是否有显著性差异,上表可以看出t值为-4.687,p值远小于0.05所以地区1和地区2的销量有显著性差异并且地区1与地区2的均值差值为负数,说明地区2的均值更大,从侧面说明地区2的销量更好。
“品牌”事后多重比较:
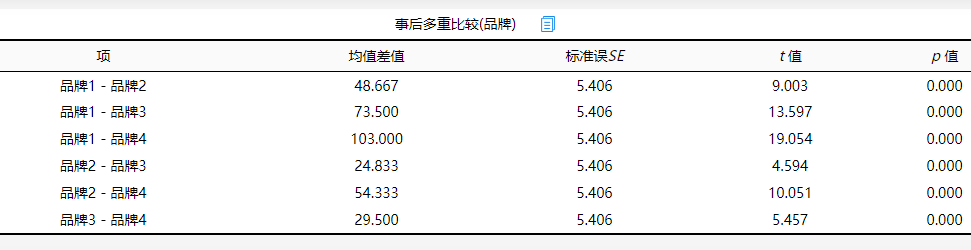
比较不同品牌的销量是否有显著性差异,上表可以看出品牌1、品牌2、品牌3、品牌4两两之间比较,p值均远小于0.05所以不同品牌两两之间的销量均有显著性差异,并且从均值差值中可以看出品牌1的均值更大,从侧面说明品牌1的销量更好。
六、总结
通过双因素方差分析研究了“品牌和地区对吸尘器的销售量是否有显著差异以及两个因素搭配是否对销售量产生新的影响”,最后发现品牌和地区对吸尘器的销售量有显著性差异,但是两个因素搭配并未对对销售量产生新的影响,并且利用事后多重比较进一步分析发现不同地区对销售量有显著性差异,并且地区2销量更好,不同品牌两两之间的销量均有显著性差异品牌1的销量更好,所以公司在做决策时可以重点分析地区2和品牌1的特点或者策略等。
相关文章:

双因素方差分析全流程
上篇文章讲述了“单因素方差分析全流程总结”,单因素方差分析只是考虑了一个自变量(定类)与一个因变量(定量)之间的关系,但是在实际问题研究中可能研究两个或者几个因素与因变量之间的关系,例如…...

微信公众号抽奖怎么做_分享微信抽奖小程序制作的好处
在H5游戏中,抽奖是最受消费者喜爱的模式之一。将H5微信抽奖活动结合到营销中,可以带来意想不到的效果,带流量和曝光率,所以许多企业也会在做活动时添加上不同类型的H5微信抽奖活动。编辑那么,新手怎么搭建微信抽奖活动…...
逻辑回归—分类问题的操作顺序
对于二元分类问题来说,分类的结果和数据的特征之间仍呈现相关关系,但是y的值不再是连续的,是0~1的跃迁。但是在这个过程中,什么仍然是连续的呢?”是概率,概率是逐渐升高的,当达到一个…...

查询服务器tns文件路径,oracle数据库tns配置方法详解
查询服务器tns文件路径,oracle数据库tns配置方法详解 TNS简要介绍与应用 Oracle中TNS的完整定义:transparence Network Substrate透明网络底层, 监听服务是它重要的一部分,不是全部,不要把TNS当作只是监听器。 TNS是Oracle Net…...

【数据结构】链表
目录 数据结构之链表:: SList.h 1.链表的概念及结构 2.链表的分类 SList.c 3.动态申请一个结点 4.单链表打印 5.单链表销毁 6.单链表头插 7.单链表头删 8.单链表尾插 9.单链表尾删 10.单链表查找 11.单链表在pos之前插入…...

一文讲明Hystrix熔断器
前言 解决问题: 主要防止服务器集群发生雪崩, 起到对服务器的保护作用 GitHub地址:https://github.com/Netflix/Hystrix/wiki 1 Hystrix是什么 1.1 分布式系统面临的问题 复杂分布式体系结构中的应用程序有数十个依赖关系,每个依赖关系在某些时候将不…...

第12篇:Java类核心构成要素分析
目录 1、Java类构成要素 1.1 如何定义类 1.2 如何定义变量 1.2.1 类变量 1.2.2 实例变量...
记一次 .NET 某医保平台 CPU 爆高分析
一:背景 1. 讲故事 一直在追这个系列的朋友应该能感受到,我给这个行业中无数的陌生人分析过各种dump,终于在上周有位老同学找到我,还是个大妹子,必须有求必应 😁😁😁。 妹子公司的…...

滤波算法 | 无迹卡尔曼滤波(UKF)算法及其MATLAB实现
目录简介UKF滤波滤波流程和公式MATLAB程序结论简介 本文接着分享位姿跟踪和滤波算法中用到的一些常用程序,希望为后来者减少一些基础性内容的工作时间。以往分享总结见文章:位姿跟踪 | 相关内容目录和链接总结(不断更新中~~~) 本…...
JAVA开发(运行JAR包怎么指定虚拟机内存大小)
我们都使用过 java -jar xxx.jar包去运行jar包。但是有时候要指定jar包运行时内存,该怎么做,而且设置多大怎么衡量,很多人从来没有了解过。 背景: 我们开发java程序,可能涉及到开发环境,测试环境&#x…...

领导力的终极奥义
过去,我曾多次演讲、著书,把自己在长达半个世纪的经营实践中所体悟到的经营思想和方法告诉中国的企业家。 但是,对于任何一家企业来说,不管它倡导了多么高尚的经营哲学,不管它构建了多么精致的管理系统,这样…...
1-MATLAB APP Design-图像的输入与输出
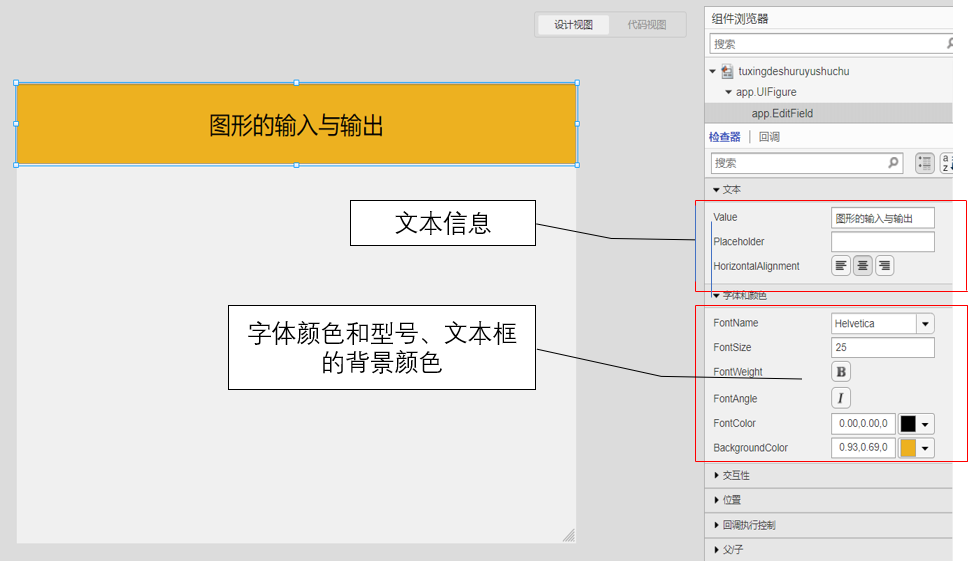
一、APP 界面设计展示 新建一个空白的APP,在此次的学习中,我们会用到编辑字段(文本框)、 按钮、坐标区和面板,首先在界面中拖入一个编辑字段(文本框),在文本框中输入内容:图形的输入与输出,调整背景颜色,字体的颜色为黑色,字体的大小调为25....
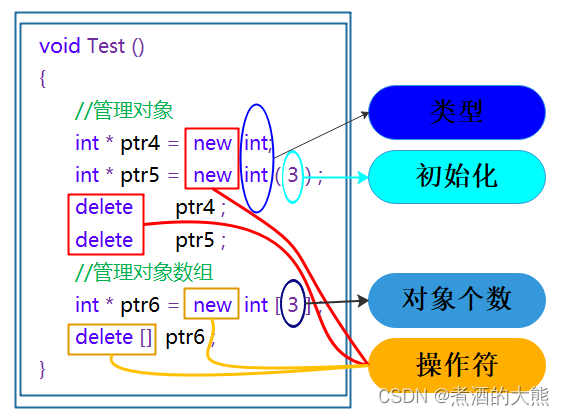
【C++】内存管理
目录一、C/C内存分布二、C内存管理方式2.1、new/delete操作内置类型2.2、new和delete操作自定义类型三、operator new与operator delete函数3.1、operator new与operator delete函数四、new和delete的实现原理4.1、内置类型4.2、自定义类型五、定位new表达式(placement-new)六、…...

Dilworth定理
偏序关系 设RRR是集合AAA的一个二元关系,若RRR满足: 1.自反性:∀x∈A\forall x \in A∀x∈A,有xRxxRxxRx 2.反对称性:∀x,y∈A\forall x,y \in A∀x,y∈A,若xRy,yRxxRy,yRxxRy,yRx,则xyxyxy 3.传递性&…...
使用loading动画让你的条件渲染页面更高级
前言在我们做项目的使用常常会使用条件渲染去有选择的给用户展示相关页面,如果渲染的数据或场景比较多比较复杂,那么往往需要3、4s的时间去完成,用户点击了之后就会陷入3、4s的空白期,并且这段时间屏幕是处于一种”未响应“的状态…...
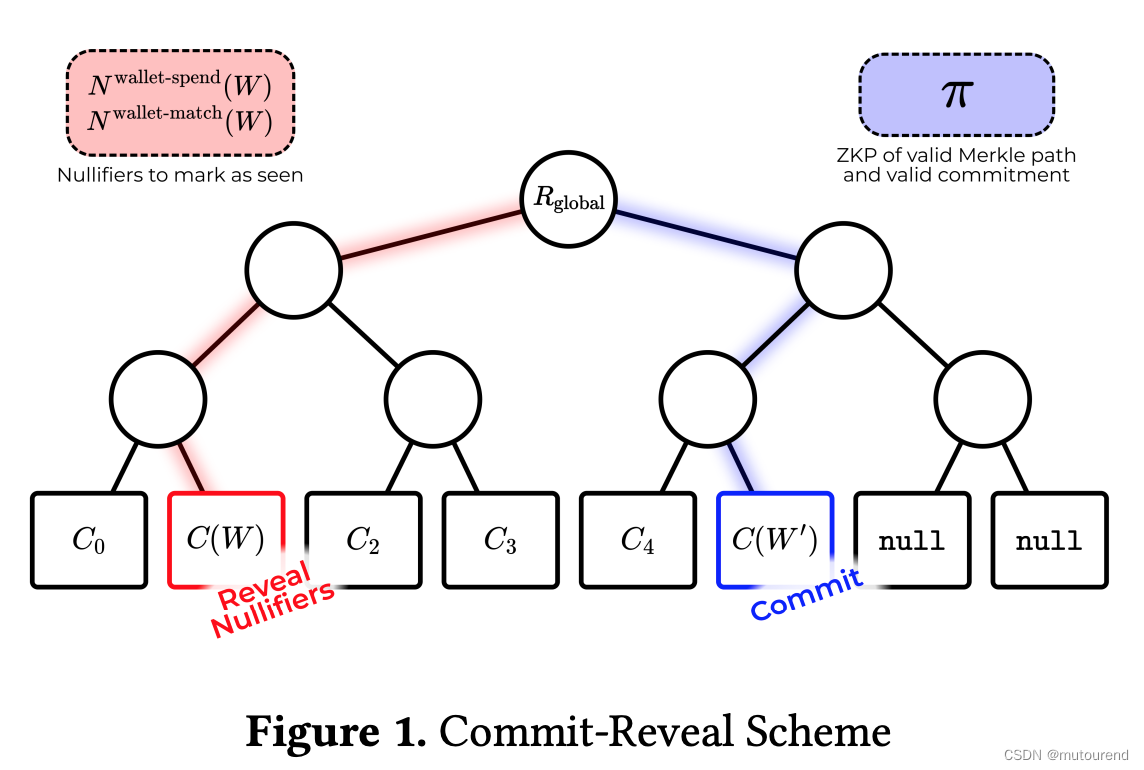
Renegade:基于MPC+Bulletproofs构建的anonymous DEX
1. 引言 白皮书见: Renegade Whitepaper: Protocol Specification, v0.6 开源代码见: https://github.com/renegade-fi/renegade(Renegade p2p网络每个节点的核心网络和密码逻辑)https://github.com/renegade-fi/mpc-bulletpr…...

二、Plugin The chain/event/query function
The chain function 链函数是所有数据处理都在其中进行的函数。在简单过滤器的情况下(本节示例的情况),_chain()函数大多是线性函数——因此对于每个传入的缓冲区,也将输出一个缓冲区。下面是一个非常简单的chain函数的实现: sta…...

了解 PostgreSQL 的扩展查询协议
1.介绍 本篇博客用于解释扩展协议的工作原理以及它与简单查询的区别。 2.简单查询 在PostgreSQL中,客户端连接能够发起两种类型的查询:简单查询和扩展协议查询。 简单查询顾名思义。 当启动 psql 客户端连接到pg服务器时,几乎所有发送的…...

接入网关和隔离网关
文章目录1. 什么是网关?2. 网关的作用是什么?3. 接入网关和隔离网关1. 什么是网关? 网关(Gateway)是一种网络设备,通常用于将不同网络之间的流量进行转发和路由,将一个网络连接到另一个网络&…...

实用指南:如何在Anolis OS上轻松使用 Kata 安全容器?
文/云原生SIG本篇文章我们将详细介绍怎么轻松在 Anolis OS 上使用 Kata Containers 安全容器,我们将介绍 Kata Container 社区于 2022 年 10 月 10 日最新发行的 Kata3.0.0 的安装部署方式,3.0.0 版本包含了基于袋鼠 RunD 开源的最新 Rust Kata runtime …...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...
