Dilworth定理
偏序关系
设RRR是集合AAA的一个二元关系,若RRR满足:
1.自反性:∀x∈A\forall x \in A∀x∈A,有xRxxRxxRx
2.反对称性:∀x,y∈A\forall x,y \in A∀x,y∈A,若xRy,yRxxRy,yRxxRy,yRx,则x=yx=yx=y
3.传递性:∀x,y,z∈A\forall x,y,z\in A∀x,y,z∈A,若xRy,yRzxRy,yRzxRy,yRz,则xRzxRzxRz
则称RRR为AAA上的偏序关系,通常记作⪯\preceq⪯
偏序集
偏序集合(Partially ordered set,Poset)是数学中,特别是序理论中,指配备了偏序关系的集合
链
设若干元素构成一个集合,那么这个集合是链当且仅当这个集合的所有元素两两可比
反链
对一个集合,它是反链当且仅当这个集合里的元素两两不可比
极大元
设偏序集AAA,x∈Ax\in Ax∈A,∄y∈A,x≠y,s.t.x⪯y\not\exists y\in A,x\neq y, s.t.\ x\preceq y∃y∈A,x=y,s.t. x⪯y,则xxx为极大元
Dilworth定理
设PPP是一个有限的偏序集,则
min{m∣∃链C1,C2,⋯,Cm,P=∪i=1mCi}=max{∣A∣:A是反链}\min\left\{m|\exists 链C_1,C_2,\cdots,C_m,P = \cup_{i=1}^{m}C_i\right\}=\max\left\{\left|A\right|:A是反链\right\} min{m∣∃链C1,C2,⋯,Cm,P=∪i=1mCi}=max{∣A∣:A是反链}
偏序集能划分成的最少的链的个数与最大反链的元素个数相等
证明:
首先证明max{∣A∣}≤min{m}\max\left\{\left|A\right|\right\}\le \min\left\{m\right\}max{∣A∣}≤min{m}
假设max{∣A∣}>min{m}\max\left\{\left|A\right|\right\}> \min\left\{m\right\}max{∣A∣}>min{m}
存在∃x,y∈A,s.t.x,y∈Ci\exists x,y \in A,s.t.\ x,y\in C_i∃x,y∈A,s.t. x,y∈Ci
说明x,yx,yx,y是可比的,与反链定义矛盾
同时我们也可以得出∣Ci∩A∣=1\left|C_i\cap A\right| = 1∣Ci∩A∣=1
接着我们对∣P∣\left|P\right|∣P∣进行归纳,来证明可以取等
当∣P∣=0,1\left|P\right| = 0,1∣P∣=0,1时,显然成立
假设∣P∣=k\left|P\right| = k∣P∣=k时成立
当∣P∣=k+1\left|P\right| = k + 1∣P∣=k+1时
设最大反链长度是mmm
最长的链是C={x1,x2,⋯,xp}C=\left\{x_1,x_2,\cdots, x_p\right\}C={x1,x2,⋯,xp},满足x1⪯x2⪯⋯⪯xpx_1 \preceq x_2\preceq \cdots \preceq x_px1⪯x2⪯⋯⪯xp
换句话说我们不能再往CCC中增加元素,也可以得出xpx_pxp是极大元
接下来分类讨论
当P\CP\backslash CP\C的每一条反链都的元素个数≤m−1\le m-1≤m−1
由于∣P\C∣<k\left|P\backslash C\right| <k∣P\C∣<k,由归纳P\CP\backslash CP\C可以划分为m−1m-1m−1个链,即P\C=∪i=1mCiP\backslash C = \cup_{i=1}^{m}C_iP\C=∪i=1mCi
那么PPP可以划分为P=C∪∪i=1mCiP = C\cup \cup_{i=1}^{m}C_iP=C∪∪i=1mCi,结论成立
当P\CP\backslash CP\C中存在反链A={a1,a2,⋯,am}A = \left\{a_1,a_2,\cdots,a_m\right\}A={a1,a2,⋯,am}时
令
P−={x∈P∣∃i,x⪯ai}P+={x∈P∣∃i,ai⪯x}P^{-} = \left\{x\in P\mid \exists i ,x \preceq a_i\right\}\\ P^{+} = \left\{x\in P\mid \exists i ,a_i\preceq x\right\}\\ P−={x∈P∣∃i,x⪯ai}P+={x∈P∣∃i,ai⪯x}
我们可以得出
1.P=P−∪P+P = P^{-} \cup P^{+}P=P−∪P+(否则存在元素与反链中的元素不可比,则这条反链不是最大的,矛盾)
2.P−∩P+=AP^{-}\cap P^{+} = AP−∩P+=A (因为ai⪯aia_i \preceq a_iai⪯ai,所以ai∈P−,ai∈P+a_i \in P^{-},a_i \in P^{+}ai∈P−,ai∈P+)
3.xp∉P−x_p \notin P^{-}xp∈/P−(反则xpx_pxp不是极大元)
AAA是P−P^{-}P−的一条最大反链,由归纳P−P^{-}P−可以划分为mmm条链C1−1,C2−,⋯,Cm−C_1^{-1},C_2^{-},\cdots, C_m^{-}C1−1,C2−,⋯,Cm−
由于∣A∩Ci−∣=1\left|A\cap C_i^{-}\right| = 1A∩Ci−=1,不妨假设ai∈Ci−a_i \in C_i^{-}ai∈Ci−
我们可以得出,aia_iai是Ci−C_i^{-}Ci−的最大元
(否则,不妨假设x∈Ci−x\in C_i^{-}x∈Ci−满足ai⪯xa_i \preceq xai⪯x,由于x∈P−x \in P^{-}x∈P−,∃aj,s.t.x⪯aj(ai≠aj)\exists a_j,s.t.\ x\preceq a_j(a_i\neq a_j)∃aj,s.t. x⪯aj(ai=aj),进而ai⪯x⪯aja_i \preceq x \preceq a_jai⪯x⪯aj,与反链定义矛盾)
同理P+P^{+}P+也可以划分为C1+,C2+,⋯,Cm+C_1^{+},C_2^{+},\cdots,C_m^{+}C1+,C2+,⋯,Cm+,aia_iai是Ci+C_i^+Ci+的极小元
令Ci=Ci−∪Ci+C_i = C_i^{-} \cup C_i^+Ci=Ci−∪Ci+,则PPP可以划分为C1,C2,⋯,CmC_1, C_2,\cdots, C_mC1,C2,⋯,Cm这mmm条链
得证
洛谷P1020
最长不上升子序列
设A=[a1,a2,⋯,an]A= [a_1,a_2,\cdots, a_n]A=[a1,a2,⋯,an]
定义偏序关系ai⪯aj⇔i≤j且ai≥aja_i \preceq a_j \Leftrightarrow i\le j 且 a_i \ge a_jai⪯aj⇔i≤j且ai≥aj(容易验证满足偏序关系)
这个偏序关系就对应了最长不上升序列
最长不上升序列就是在求最长的链
划分最长不上升序列的个数最少为最长上升子序列长度
#include<cstdio>
#include<algorithm>
#include<functional>const int N = 1e5 + 5;int dp1[N];
int dp2[N];int main() {bool flag = false;int t, idx, ans1 = 1, ans2 = 1;while (~scanf("%d", &t)) {if (!flag) {flag = true;dp1[1] = dp2[1] = t;continue;}if (dp1[ans1] >= t) {++ans1;dp1[ans1] = t;}else {int idx = std::upper_bound(dp1 + 1, dp1 + 1 + ans1, t, std::greater<int>()) - dp1;dp1[idx] = t;}if (t > dp2[ans2]) {++ans2;dp2[ans2] = t;}else {int idx = std::lower_bound(dp2 + 1, dp2 + 1 + ans2, t) - dp2;dp2[idx] = t;}}printf("%d\n%d\n", ans1, ans2);return 0;
}
https://www.cnblogs.com/itlqs/p/6636222.html
https://cmwqf.github.io/2019/12/17/%E6%B5%85%E8%B0%88Dilworth%E5%AE%9A%E7%90%86/
https://www.math.cmu.edu/~af1p/Teaching/Combinatorics/F03/Class14.pdf
相关文章:

Dilworth定理
偏序关系 设RRR是集合AAA的一个二元关系,若RRR满足: 1.自反性:∀x∈A\forall x \in A∀x∈A,有xRxxRxxRx 2.反对称性:∀x,y∈A\forall x,y \in A∀x,y∈A,若xRy,yRxxRy,yRxxRy,yRx,则xyxyxy 3.传递性&…...
使用loading动画让你的条件渲染页面更高级
前言在我们做项目的使用常常会使用条件渲染去有选择的给用户展示相关页面,如果渲染的数据或场景比较多比较复杂,那么往往需要3、4s的时间去完成,用户点击了之后就会陷入3、4s的空白期,并且这段时间屏幕是处于一种”未响应“的状态…...
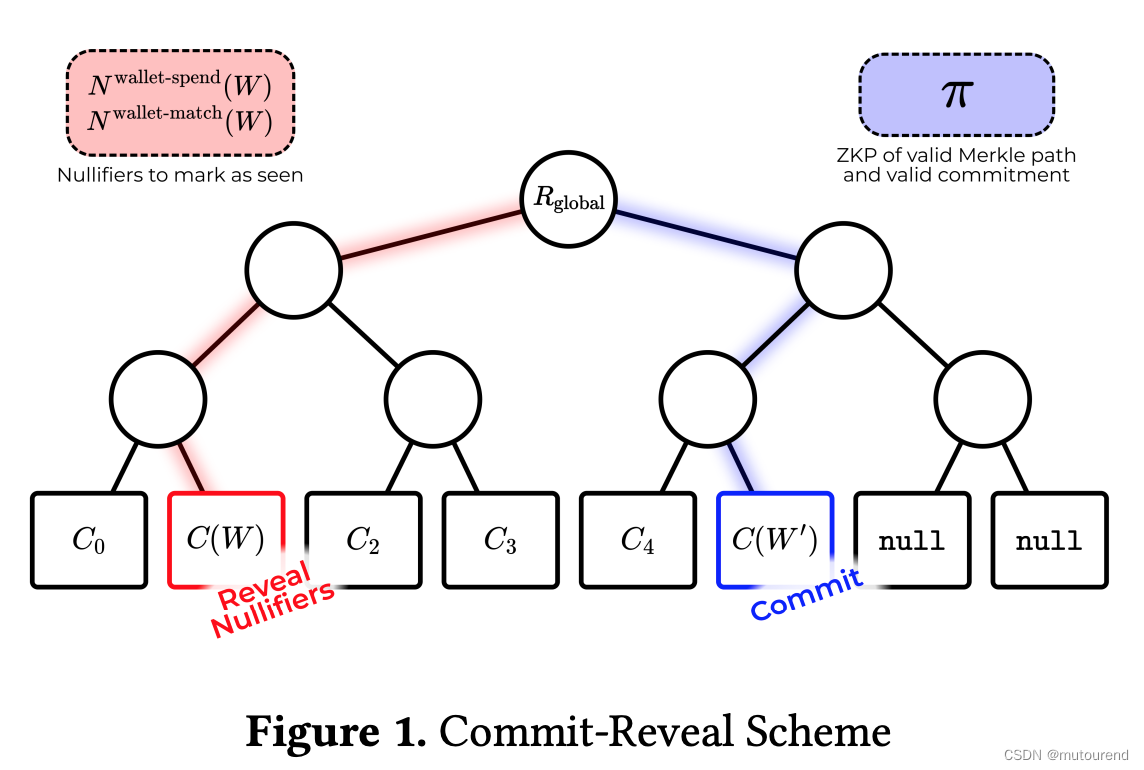
Renegade:基于MPC+Bulletproofs构建的anonymous DEX
1. 引言 白皮书见: Renegade Whitepaper: Protocol Specification, v0.6 开源代码见: https://github.com/renegade-fi/renegade(Renegade p2p网络每个节点的核心网络和密码逻辑)https://github.com/renegade-fi/mpc-bulletpr…...

二、Plugin The chain/event/query function
The chain function 链函数是所有数据处理都在其中进行的函数。在简单过滤器的情况下(本节示例的情况),_chain()函数大多是线性函数——因此对于每个传入的缓冲区,也将输出一个缓冲区。下面是一个非常简单的chain函数的实现: sta…...

了解 PostgreSQL 的扩展查询协议
1.介绍 本篇博客用于解释扩展协议的工作原理以及它与简单查询的区别。 2.简单查询 在PostgreSQL中,客户端连接能够发起两种类型的查询:简单查询和扩展协议查询。 简单查询顾名思义。 当启动 psql 客户端连接到pg服务器时,几乎所有发送的…...

接入网关和隔离网关
文章目录1. 什么是网关?2. 网关的作用是什么?3. 接入网关和隔离网关1. 什么是网关? 网关(Gateway)是一种网络设备,通常用于将不同网络之间的流量进行转发和路由,将一个网络连接到另一个网络&…...

实用指南:如何在Anolis OS上轻松使用 Kata 安全容器?
文/云原生SIG本篇文章我们将详细介绍怎么轻松在 Anolis OS 上使用 Kata Containers 安全容器,我们将介绍 Kata Container 社区于 2022 年 10 月 10 日最新发行的 Kata3.0.0 的安装部署方式,3.0.0 版本包含了基于袋鼠 RunD 开源的最新 Rust Kata runtime …...

如何锁定Word文档部分文字不被修改
我们知道,想要保护Word文档的内容无法随意更改,可以设置“限制编辑”的保护模式。 那如果实际工作中,只需要固定的一部分内容不能编辑,可以实现吗?答案是肯定的,今天就来说说如何设置Word文档部分文字可修…...

聊聊8万8的私董会,很扎心
聊聊8万8的私董会,很扎心 道几句真心话,很扎心,但也很现实。 如果你喜欢刷抖音,这种感觉应该会更加明显。 股市哀鸿遍野,实体一地鸡毛,我们办公室楼下的门面换了一波又一波。 别说那些不起眼的小生意&a…...
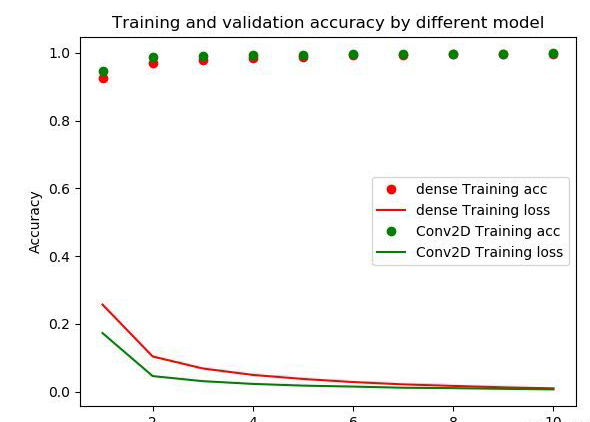
卷积网络与全连接网络的区别
问题卷积神经网络是一类包含卷积计算且具有深度结构的前馈神经网络,是深度学习。卷积神经网络具有表征学习能力,能够按其阶层结构对输入信息进行平移不变分类,因此也被称为“平移不变人工神经网络。全连接神经网络是具有多层感知器的的网络&a…...

【5000左右电脑配置清单】预算不高于5000,不带显示器的电脑配置清单推荐
由于本人是学生党经济有限,预算不高于5000元配一套电脑主机,说实话5000左右的电脑配置已经很好了,今天站长整理了几款配置给大家参考参考,更多电脑配置还请继续关注西安SEO优化站点! 配置1: <CPU> I5…...
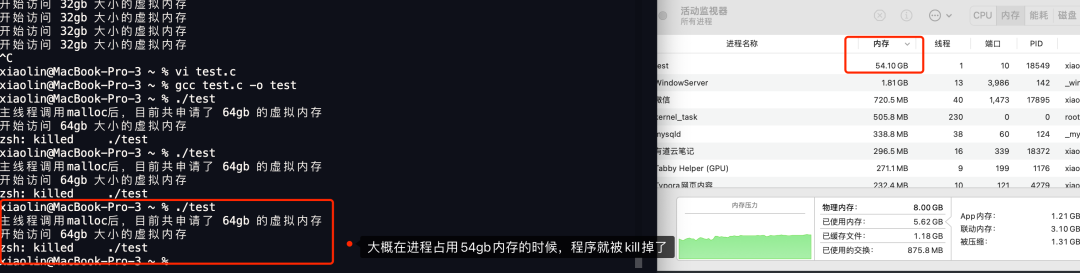
在 4G 内存的机器上,申请 8G 内存会怎么样?
在 4GB 物理内存的机器上,申请 8G 内存会怎么样? 这个问题在没有前置条件下,就说出答案就是耍流氓。这个问题要考虑三个前置条件: 操作系统是 32 位的,还是 64 位的?申请完 8G 内存后会不会被使用&#x…...
JavaSE学习day9 集合(基础班结束)
1.ArrayList 集合和数组的优势对比: 长度可变 添加数据的时候不需要考虑索引,默认将数据添加到末尾 不能存基本数据类型。只能通过包装。 1.1ArrayList类概述 什么是集合 提供一种存储空间可变的存储模型,存储的数据容量可以发生改变 Ar…...
Python爬虫进阶 - win和linux下selenium使用代理
目录 Windows selenium配置 下载地址 Chrome Chromedriver 版本对应关系 实践测试 操作元素 浏览器操作 获取元素信息 鼠标操作 实战demo selenium添加代理 Linux selenium配置 检查服务器环境 下载安装第三方库(最简单版) 实践测试 代码…...

力扣-从不订购的客户
大家好,我是空空star,本篇带大家了解一道简单的力扣sql练习题。 文章目录前言一、题目:183. 从不订购的客户二、解题1.正确示范①提交SQL运行结果2.正确示范②提交SQL运行结果3.正确示范③提交SQL运行结果4.正确示范④提交SQL运行结果总结前言…...

速来!掘金数据时代2022年度隐私计算评选活动火热报名中!
开放隐私计算 开放隐私计算开放隐私计算OpenMPC是国内第一个且影响力最大的隐私计算开放社区。社区秉承开放共享的精神,专注于隐私计算行业的研究与布道。社区致力于隐私计算技术的传播,愿成为中国 “隐私计算最后一公里的服务区”。183篇原创内容公众号…...

Springboot @Test 给Controller接口 写 单元测试
前言 最近有小伙伴问到怎么给 controller的接口写单元测试。 单元测试是开发必不可少的一个环节。 既然有人问到了,那我觉得可能不止一个人不会,那就按照惯例,出手。 正文 内容: 主要是get 和 post 两种请求方式的接口 的 单元测…...

ISO 6721-1~12 ,塑料-电动机械性能的测定,2022更新
ISO 6721-1 :2019 Plastics - Determination of dynamic mechanical properties - Part 1: General principles ISO 6721-1 :2019 塑料 - 电动机械性能的测定. 第1部分:一般原理 ISO 6721-2 :2019 Plastics — Determination of dynamic mechanical properties — Part 2:…...

vue3.2中使用swiper缩略图轮播教程
介绍 在vue3 中使用 swiper 实现缩略图的轮播图效果,具体如下图所示: 使用 切换到项目终端 ,输入命令 npm install swiper --save , 进行安装在 main.js里,引入 swiper.css并使用,具体代码如下;import {createApp } from vue import App from ./App.vue import router…...

边玩边学,13个 Python 小游戏真有趣啊(含源码)
经常听到有朋友说,学习编程是一件非常枯燥无味的事情。其实,大家有没有认真想过,可能是我们的学习方法不对? 比方说,你有没有想过,可以通过打游戏来学编程? 今天我想跟大家分享几个Python小游…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...
