速来!掘金数据时代2022年度隐私计算评选活动火热报名中!
开放隐私计算


开放隐私计算
开放隐私计算OpenMPC是国内第一个且影响力最大的隐私计算开放社区。社区秉承开放共享的精神,专注于隐私计算行业的研究与布道。社区致力于隐私计算技术的传播,愿成为中国 “隐私计算最后一公里的服务区”。
183篇原创内容
公众号


评选背景
自2021年起,《数据安全法》与《个人信息保护法》陆续落地,数据在数字经济中作为关键生产要素,逐渐成为共识。用于平衡数据利用与安全的技术--隐私计算,已迈向高速落地应用阶段。
中国的隐私计算起步晚,但发展迅猛。据全球权威知识产权第三方机构IPRdaily与incoPat数据,截至2022年3月,全球隐私计算专利数量前10名企业中,有6家企业来自中国。行业先行者的领跑,带动隐私计算行业相关基础设施和技术的完善,也推动了国内用户对数据安全的重视与需求。
值得注意的是,2022年也被称为“隐私计算开源之年”。目前国内已有微众银行、蚂蚁集团、原语科技等企业推出了多个隐私计算开源项目,隐私计算技术的应用门槛得以迅速降低,催生出更多隐私计算产品供应商,行业竞争强度的提高,也进一步促进隐私计算技术的普及、应用和发展。
在创投领域,隐私计算赛道热度依旧不减,仅2022年就有多起资金规模上亿元的投资事件,参与投资方包含顶级财务投资机构、国资背景基金以及知名产业投资方。
在政策主导,市场多方力量的驱动下,隐私计算开始规模化的应用到产品和解决方案中,加速数据要素在具体场景内的落地应用。数据要素产业百花齐放,隐私计算商业化发展思路随之发生改变。
可以预见的是,2023年隐私计算赛道会有更多从业者的加入,市场将迎来更多元化的参与者。隐私计算在金融、政务、通信运营商、医疗等领域的应用,不只局限于平台建设,还可以挖掘出更多融合在具体生产场景中的新需求。
回望过去的2022年,无论是企业,还是从业者,抑或投资机构,都在努力将数据要素市场这份“蛋糕”做大,多方主体不断在追求数据的安全合规的应用,促进数据要素产业健康蓬勃发展。
对于创业者来讲,2022年隐私计算落地应用加速,行业机遇蕴藏在广阔的场景中,金融、银行、保险等产业是热门行业,更多待开发的产业场景亦有巨大空间。
对于投资机构来讲,隐私计算领域的优秀企业炙手可热。通过自己的行业深刻认知以及资金、产业资源等发掘优秀的商业模式,并找到有能力的创业者,投资并与其同行,是收获产业商业价值极佳方式。数据要素产业广阔天地,大有可为!

评主题&申报入口





END
往期推荐:
隐私计算头条周刊(2.6-2.12)
近期隐私计算行业招聘
2023年网络安全十大发展趋势发布:涉及隐私计算、数据安全
安全多方学习开源框架调研
开放隐私计算社区征稿啦!
热门文章:
姚期智院士:数据、算法、算力为何是数字经济核心技术?
隐私计算又遇技术突破,亿级数据密态分析可在10分钟内完成
清华大学张超:实现数据确权与保护,数据密态渐成行业共识
数据确权:第五要素的战争
未来十年,将会有95%的企业采用隐私计算技术
阅读 108
分享收藏32
分享此内容的人还喜欢
数据资产管理建设思考(二)
转型数据治理阅读 1024不喜欢
不看的原因确定
内容质量低
不看此公众号
数据指标体系思考(四)
转型数据治理阅读 1403不喜欢
不看的原因确定
内容质量低
不看此公众号

相关文章:

速来!掘金数据时代2022年度隐私计算评选活动火热报名中!
开放隐私计算 开放隐私计算开放隐私计算OpenMPC是国内第一个且影响力最大的隐私计算开放社区。社区秉承开放共享的精神,专注于隐私计算行业的研究与布道。社区致力于隐私计算技术的传播,愿成为中国 “隐私计算最后一公里的服务区”。183篇原创内容公众号…...

Springboot @Test 给Controller接口 写 单元测试
前言 最近有小伙伴问到怎么给 controller的接口写单元测试。 单元测试是开发必不可少的一个环节。 既然有人问到了,那我觉得可能不止一个人不会,那就按照惯例,出手。 正文 内容: 主要是get 和 post 两种请求方式的接口 的 单元测…...

ISO 6721-1~12 ,塑料-电动机械性能的测定,2022更新
ISO 6721-1 :2019 Plastics - Determination of dynamic mechanical properties - Part 1: General principles ISO 6721-1 :2019 塑料 - 电动机械性能的测定. 第1部分:一般原理 ISO 6721-2 :2019 Plastics — Determination of dynamic mechanical properties — Part 2:…...

vue3.2中使用swiper缩略图轮播教程
介绍 在vue3 中使用 swiper 实现缩略图的轮播图效果,具体如下图所示: 使用 切换到项目终端 ,输入命令 npm install swiper --save , 进行安装在 main.js里,引入 swiper.css并使用,具体代码如下;import {createApp } from vue import App from ./App.vue import router…...

边玩边学,13个 Python 小游戏真有趣啊(含源码)
经常听到有朋友说,学习编程是一件非常枯燥无味的事情。其实,大家有没有认真想过,可能是我们的学习方法不对? 比方说,你有没有想过,可以通过打游戏来学编程? 今天我想跟大家分享几个Python小游…...
)
MySQL数据文件迁移(不关闭SELinux)
背景 日常实施中可能会出现在部署MySQL时未更改数据默认存储路径(默认:/var/lib/mysql),然而一般分配服务器的人只会给系统分区分配50G的空间,这导致后续空间不够用的情况,也就出现了需要迁移数据的问题。…...
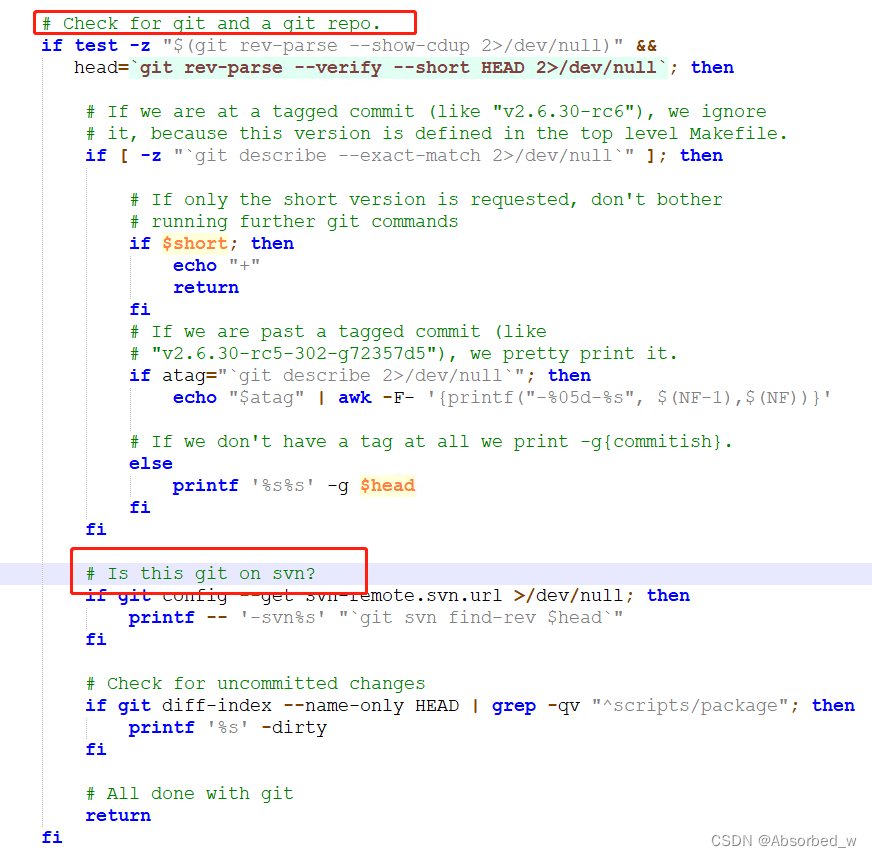
uboot / linux添加/去除 版本号LOCALVERSION
背景 偶然的机会,在insmod驱动模块的时候,遇到报错: 查找原因,说是当前系统内核版本和模块编译使用版本不同! 使用如下命令查看当前系统内核版本: uname -r 使用modinfo命令(嵌入式设备没有此…...

2023北京养老展,北京养老展会,北京养老产业展览会
CBIAIE第十届中国(北京)国际老年产业博览会,8月28-30日在北京亦创国际会展中心举办; 预期效果:中国(北京)国际老年产业博览会China (Beijing) International Aged industry Expo(CB…...

华为OD机试 - 分糖果(Java) | 机试题算法思路 【2023】
使用说明 参加华为od机试,一定要注意不要完全背诵代码,需要理解之后模仿写出,通过率才会高。 华为 OD 清单查看地址:https://blog.csdn.net/hihell/category_12201821.html 华为OD详细说明:https://dream.blog.csdn.net/article/details/128980730 分糖果 小明从糖果…...

带你彻底了解浮点型数据的存储
🚀🚀🚀大家觉不错的话,就恳求大家点点关注,点点小爱心,指点指点🚀🚀🚀 目录 🐰浮点型在内存的存储 🤔提示:数据类型的存储范围 &a…...

【牛客刷题专栏】0x0C:JZ4 二维数组中的查找(C语言编程题)
前言 个人推荐在牛客网刷题(点击可以跳转),它登陆后会保存刷题记录进度,重新登录时写过的题目代码不会丢失。个人刷题练习系列专栏:个人CSDN牛客刷题专栏。 题目来自:牛客/题库 / 在线编程 / 剑指offer: 目录前言问题…...
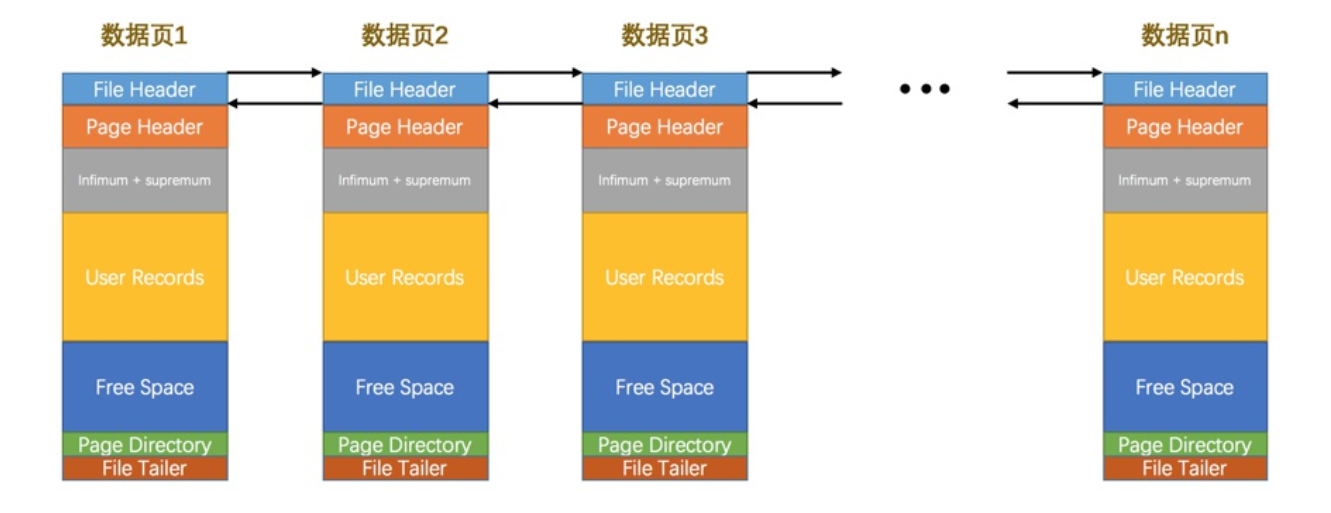
「mysql是怎样运行的」第5章 盛放记录的大盒子---InnoDB数据页结构
「mysql是怎样运行的」第五章 盛放记录的大盒子—InnoDB数据页结构 文章目录「mysql是怎样运行的」第五章 盛放记录的大盒子---InnoDB数据页结构[toc]一、不同类型的页介绍二、数据页结构的快速浏览三、记录在页中的存储记录头信息的秘密四、Page Directory(页目录)五、Page He…...
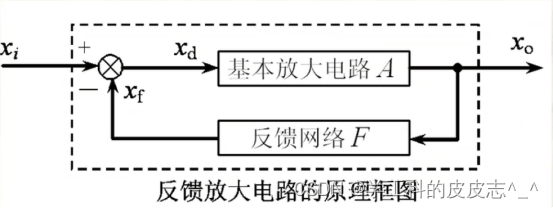
模电中的负反馈
文章目录一、反馈是什么?二、负反馈对于放大性能的影响1.负反馈的作用三、正反馈总结– 一、反馈是什么? 反馈的定义:凡是将放大电路输出端信号(电压或电流)的一部分或者全部引回到输入端,与输入信号叠加…...
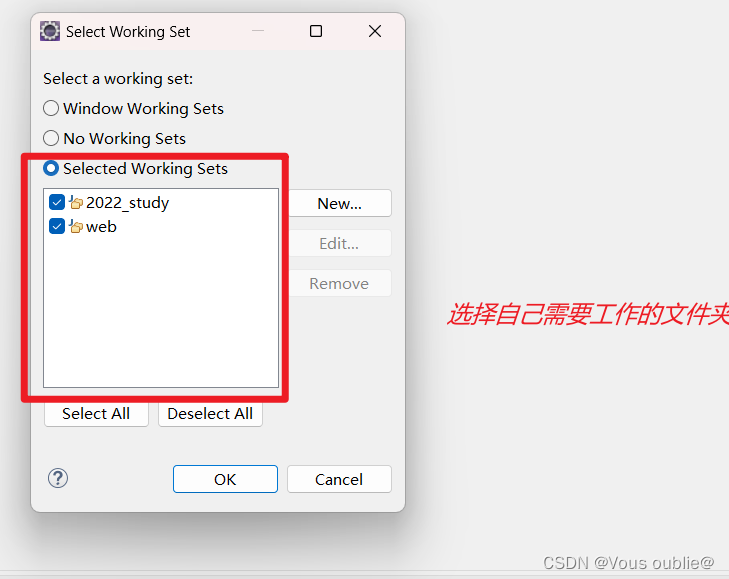
eclipse中整理左侧项目栏文件
💡在使用eclipse的过程中,随着项目越来越多,会使得项目管理变得困难,介绍一下eclipse中对于项目分类存放(Java Working Set)的解决方案。如果按照默认的方式查看项目列表是这种效果:⭕当创建使用小项目过多…...
IDEA性能优化设置(解决卡顿问题)修改内存
在我们日常使用IDEA进行开发时,可能会遇到许多卡顿的瞬间,明明我们的机器配置也不低啊?为什么就会一直卡顿呢? 原来这是因为IDEA软件在我们安装的时候就设置了默认的内存使用上限(通常很小),这就…...

Android ABI
概念 不同的 Android 设备使用不同的 CPU,而不同的 CPU 支持不同的指令集。CPU 与指令集的每种组合都有专属的应用二进制接口 (ABI)。ABI 包含以下信息: 可使用的 CPU 指令集(和扩展指令集)。运行时内存存储和加载的字节顺序。Android 始终是 little-endian。在应用和系统…...

决策树算法和CART决策树算法详细介绍及其原理详解
相关文章 K近邻算法和KD树详细介绍及其原理详解朴素贝叶斯算法和拉普拉斯平滑详细介绍及其原理详解决策树算法和CART决策树算法详细介绍及其原理详解 文章目录相关文章前言一、决策树算法二、CART决策树算法2.1 基尼系数2.2 CART决策树算法总结前言 今天给大家带来的主要内容包…...
ChatGPT风口下的中外“狂飙”,一文看懂微软、谷歌、百度、腾讯、华为、字节跳动们在做什么?
毫无疑问,ChatGPT正成为搅动市场情绪的buzzword。 历史经历过无线电,半导体,计算机,移动通讯,互联网,移动互联网,社交媒体,云计算等多个时代,产业界也一直在寻找Next Big…...

前端的核心技术有哪些?
前端即网站前台部分,运行在PC端,移动端等浏览器上展现给用户浏览的网页。随着互联网技术的发展,HTML5,CSS3,前端框架的应用,跨平台响应式网页设计能够适应各种屏幕分辨率,合适的动效设计&#x…...

Talk预告 | 悉尼科技大学澳大利亚人工智能研究所讲师方震:广义分布外检测的学习理论
本期为TechBeat人工智能社区第476期线上Talk! 北京时间2月22日(周三)20:00,悉尼科技大学澳大利亚人工智能研究所讲师——方震的Talk将准时在TechBeat人工智能社区开播! 他与大家分享的主题是: “广义分布外检测的学习理论”,届时将…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...

二维FDTD算法仿真
二维FDTD算法仿真,并带完全匹配层,输入波形为高斯波、平面波 FDTD_二维/FDTD.zip , 6075 FDTD_二维/FDTD_31.m , 1029 FDTD_二维/FDTD_32.m , 2806 FDTD_二维/FDTD_33.m , 3782 FDTD_二维/FDTD_34.m , 4182 FDTD_二维/FDTD_35.m , 4793...
Android屏幕刷新率与FPS(Frames Per Second) 120hz
Android屏幕刷新率与FPS(Frames Per Second) 120hz 屏幕刷新率是屏幕每秒钟刷新显示内容的次数,单位是赫兹(Hz)。 60Hz 屏幕:每秒刷新 60 次,每次刷新间隔约 16.67ms 90Hz 屏幕:每秒刷新 90 次,…...
