带你彻底了解浮点型数据的存储
🚀🚀🚀大家觉不错的话,就恳求大家点点关注,点点小爱心,指点指点🚀🚀🚀
目录
🐰浮点型在内存的存储
🤔提示:数据类型的存储范围
🌸浮点型的类型:
✈️引入:
🐰浮点型数据存储的规则
🌸有效位数字M的规定
🌸10进制的小数转换成2进制的小数
🌸指数E的规定
🌸引入的解读
🐰浮点型在内存的存储
🤔提示:数据类型的存储范围
整形家族的类型的取值范围:放在limits.h的文件浮点型类型的取值范围:放在float.h的文件
🌸浮点型的类型:
float:单精度浮点型double:双精度浮点型long double:更高精度的浮点型(不常用)
✈️引入:
浮点型存储的例子#include<stdio.h> int main() {int n=9;float* pFloat=(float*)&n;printf("n的值为:%d\n",n);printf("pFloat的值为:%f\n",*pFloat);*pFloat=9.0;printf("num的值为:%d\n",n);printf("pFloat的值为:%f\n",n); }结果为:n的值为:9pFloat的值为:0.000000num的值为:1091567616pFloat的值为:0.000000
🐰浮点型数据存储的规则
num和*pFloat在内存中明明是同一个数,为什么浮点数和整数的解读结果会差别这么大?根据国际标准IEEE(电气和电子工程协会)754,任意一个二进制浮点数V可以表示成下面的形式:(-1)^S*M*(2^E) (-1)^S表示符号位,当S=0,V为正数;当S=1,V为负数 M表示有效数字,大于等于1,小于2 2^E表示指数位 举例来说: 十进制的5.0,写成二进制是101.0,相当于1.01*2^2 可以得出S=0,M=1.01,E=2 十进制的-5.0,写成二进制是-101.0,相当于-1.01*2^2 可以得出S=1,M=1.01,E=2再例如:5.5
V=5.5=(-1)^0*1.011*2^2S=0M=1.011E=2IEEE 754规定:float(单精度浮点型) 32位的浮点型对于32位的浮点数,最高的1位是符号位S,接着的8位是指数E,剩下的23位为有效数字M
double(双精度浮点型) 64位的浮点型对于64位的浮点数,最高的1位是符号位S,接着的11位是指数E,剩下的52位为有效数字M
IEEE 754对有效数字M和指数E,还有一些特别的规定🌸有效位数字M的规定
前面说过1<=M<2,也就是说,M可以写成1.xxxxxx的形式,其中xxxxxx表示小数部分。IEEE 754规定,在计算机内部保存M时,默认这个数的第一位总是1,因此可以舍去,只保存后面的xxxxxx部分。比如保存1.01的时候,只保存01,等到读取的时候,在把第一位加上去。这样做的目的,节省1位有效数字。以32位浮点数为例,留给M只有23位,将第一位的1舍去后,等于可以保存24位有效数字🌸10进制的小数转换成2进制的小数
10进制的小数乘以2,算出乘积,取出乘积的整数部分,再用2乘以余下的小数部分,又可以得到一个乘积,再取出乘积的整数部分,如此进行,直到乘积中的小数部分为零,或者达到所要求的精度为止。然后把取出的整数部分按顺序排列起来。先取的整数作为高位,后取的整数作为低位。
#include<stdio.h> int main() {float n=5.3;printf("%.10f",n);return 0; } 打印出来的值为5.3000001907🌸指数E的规定
首先,E为一个无符号整数(unsigned int)这意味着,如果E为8位,它的取值范围为0~255;如果E为11位,它的取值范围为0~2047.但是我们知道,科学计数法中的E可以是负数,所以IEEE 754规定,存入内存时的E的真实值必须再加上一个中间数,对于8位的E,这个中间数是127,对于11位的E,这个中间数是1023。比如,2^10的E是10,所以保存32位浮点数时,必须保存成10+127=137,即,10001001(无符号数)E的范围为-127~1285.5的表示,以32位为例#include<stdio.h> int main() {float n=5.5f;//5.5的二进制表示形式:101.1//V=5.5=(-1)^0*1.011*2^2//S:0 E:2(在内存存储的是2+127=129 二进制为:10000001) M:1.011(内存中真实存储的是011)//所以内存中存储的是0 10000001 01100000000000000000000//十六进制为40b00000return 0; }E从内存中取出,也得分三种情况E不全为0或不全为1(我们常见的情况)这时,浮点数就采用下面的规则表示,即指数E的计算值减去127(或1023),得到真实值,再将有效数字M前加第一位的1比如:0.5的二进制形式为0.1,由于规定正数部分必须为1,即将小数点右移1位,则为(-1)^0*1.0*2^(-1),E真实存储为-1+127=126,表示为01111110,而尾数1.0去掉整数部分为0,补齐0到23位00000000000000000000000,则其二进制表示形式为:0 01111110 00000000000000000000000E全为0这时,浮点数的指数E等于1-127(或者1-1023)即为真实值,有效数字M不再加上第一位的1,而是还原为0.xxxxxx的小数。这样做是为了表示+-0,以及接近于0的很小的数字E全为1表示+-无穷大的数(+-取决于符号位s)
🌸引入的解读
#include<stdio.h> int main() {int n=9;//00000000000000000000000000001001-9的补码//S:0 E:00000000 M:00000000000000000001001//E=1-127=-126//M=0.00000000000000000001001//(-1)^0*0.00000000000000000001001*2^-126float* pFloat=(float*)&n;printf("n的值为:%d\n",n);printf("pFloat的值为:%f\n",*pFloat);*pFloat=9.0;//00000000000000000000000000001001-9的补码//1.001*2^3//V=(-1)^0*1.001*2^3//s:0 E:3(存储的 3+127=130) M:00100000000000000000000//0 10000010 00100000000000000000000printf("num的值为:%d\n",n);//如果以整形打印的话,就会把 0 10000010 00100000000000000000000直接当成补码,打印出来,结果为1091567616printf("pFloat的值为:%f\n",n);return 0; }这样就可以理解打印的值为:
n的值为:9pFloat的值为:0.000000num的值为:1091567616pFloat的值为:0.000000
🌸🌸🌸如果大家还有不懂或者建议都可以发在评论区,我们共同探讨,共同学习,共同进步。谢谢大家! 🌸🌸🌸
相关文章:

带你彻底了解浮点型数据的存储
🚀🚀🚀大家觉不错的话,就恳求大家点点关注,点点小爱心,指点指点🚀🚀🚀 目录 🐰浮点型在内存的存储 🤔提示:数据类型的存储范围 &a…...

【牛客刷题专栏】0x0C:JZ4 二维数组中的查找(C语言编程题)
前言 个人推荐在牛客网刷题(点击可以跳转),它登陆后会保存刷题记录进度,重新登录时写过的题目代码不会丢失。个人刷题练习系列专栏:个人CSDN牛客刷题专栏。 题目来自:牛客/题库 / 在线编程 / 剑指offer: 目录前言问题…...
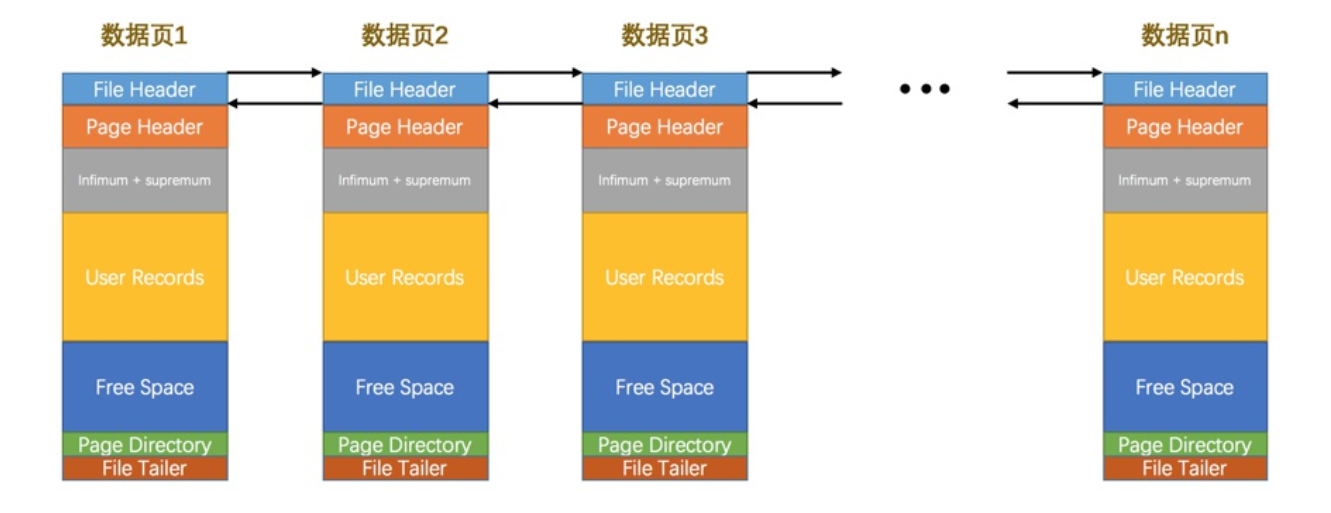
「mysql是怎样运行的」第5章 盛放记录的大盒子---InnoDB数据页结构
「mysql是怎样运行的」第五章 盛放记录的大盒子—InnoDB数据页结构 文章目录「mysql是怎样运行的」第五章 盛放记录的大盒子---InnoDB数据页结构[toc]一、不同类型的页介绍二、数据页结构的快速浏览三、记录在页中的存储记录头信息的秘密四、Page Directory(页目录)五、Page He…...
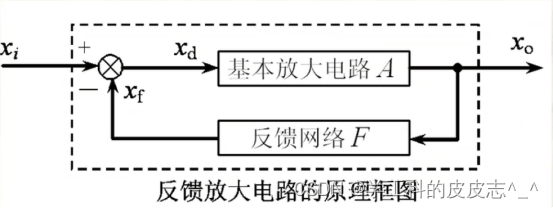
模电中的负反馈
文章目录一、反馈是什么?二、负反馈对于放大性能的影响1.负反馈的作用三、正反馈总结– 一、反馈是什么? 反馈的定义:凡是将放大电路输出端信号(电压或电流)的一部分或者全部引回到输入端,与输入信号叠加…...
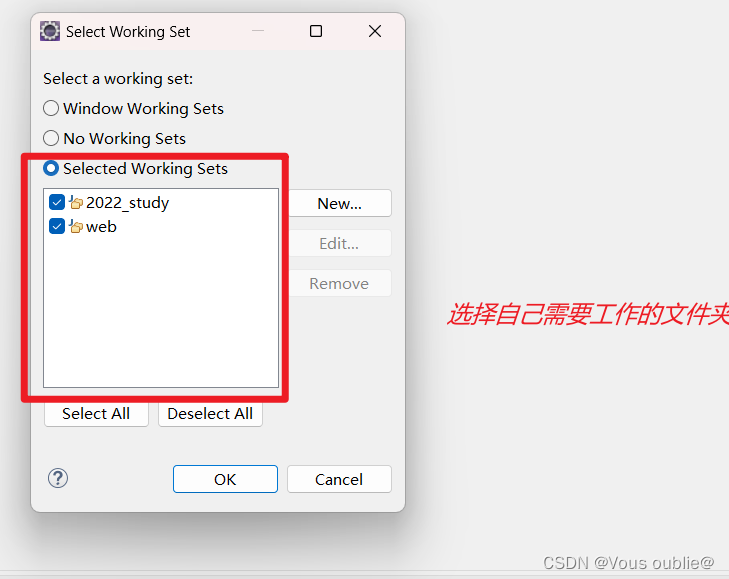
eclipse中整理左侧项目栏文件
💡在使用eclipse的过程中,随着项目越来越多,会使得项目管理变得困难,介绍一下eclipse中对于项目分类存放(Java Working Set)的解决方案。如果按照默认的方式查看项目列表是这种效果:⭕当创建使用小项目过多…...
IDEA性能优化设置(解决卡顿问题)修改内存
在我们日常使用IDEA进行开发时,可能会遇到许多卡顿的瞬间,明明我们的机器配置也不低啊?为什么就会一直卡顿呢? 原来这是因为IDEA软件在我们安装的时候就设置了默认的内存使用上限(通常很小),这就…...

Android ABI
概念 不同的 Android 设备使用不同的 CPU,而不同的 CPU 支持不同的指令集。CPU 与指令集的每种组合都有专属的应用二进制接口 (ABI)。ABI 包含以下信息: 可使用的 CPU 指令集(和扩展指令集)。运行时内存存储和加载的字节顺序。Android 始终是 little-endian。在应用和系统…...

决策树算法和CART决策树算法详细介绍及其原理详解
相关文章 K近邻算法和KD树详细介绍及其原理详解朴素贝叶斯算法和拉普拉斯平滑详细介绍及其原理详解决策树算法和CART决策树算法详细介绍及其原理详解 文章目录相关文章前言一、决策树算法二、CART决策树算法2.1 基尼系数2.2 CART决策树算法总结前言 今天给大家带来的主要内容包…...
ChatGPT风口下的中外“狂飙”,一文看懂微软、谷歌、百度、腾讯、华为、字节跳动们在做什么?
毫无疑问,ChatGPT正成为搅动市场情绪的buzzword。 历史经历过无线电,半导体,计算机,移动通讯,互联网,移动互联网,社交媒体,云计算等多个时代,产业界也一直在寻找Next Big…...

前端的核心技术有哪些?
前端即网站前台部分,运行在PC端,移动端等浏览器上展现给用户浏览的网页。随着互联网技术的发展,HTML5,CSS3,前端框架的应用,跨平台响应式网页设计能够适应各种屏幕分辨率,合适的动效设计&#x…...

Talk预告 | 悉尼科技大学澳大利亚人工智能研究所讲师方震:广义分布外检测的学习理论
本期为TechBeat人工智能社区第476期线上Talk! 北京时间2月22日(周三)20:00,悉尼科技大学澳大利亚人工智能研究所讲师——方震的Talk将准时在TechBeat人工智能社区开播! 他与大家分享的主题是: “广义分布外检测的学习理论”,届时将…...

企业微信的聊天机器人来了,免费下载(Python版)
大家好,这里是程序员晚枫,个人网址:python-office.com 上次分享了微信机器人的视频以后,视频下面有一个热门评论: 什么时候开发企业版微信机器人?自动回复、自动群发等等~ 在经历了一段时间的查找和开发以…...

DataGear 4.5.0 发布,数据可视化分析平台
DataGear 4.5.0 发布,带来数据集计算属性新功能,具体更新内容如下: 新增:数据集属性新增计算表达式功能,可对原始数据进行二次计算处理;新增:HTTP接口数据集新增文本、XML请求体类型支持&#…...

Java使用Aria2c进行文件下载
在Java服务中有复杂网络环境下下载大文件的需求,一开始自己写了一个多线程下载,但遇到校园网下载1G以上大文件时直接卡死了。 经调研后决定用aria下载器,成熟稳定,避免自己去处理各种网络问题。下面记录一下windows和ubuntu系统上…...

Dart 表达式以及语法糖汇总
前言 Dart语言中有许多语法糖或者说lambda表达式,语法和代码量是简洁了许多,但给想要入门的我添加了许多困扰,我经常看官方API或者第三方文档API的时候,在示例中大量的使用了类似的语法糖,让代码的可读性大大下降&…...

支付宝支付功能使用
1、进入“蚂蚁金服开放平台” https://open.alipay.com/https://open.alipay.com/ 2、下载支付宝官方 demo,进行配置和测试 文档地址 手机网站支付 DEMO | 网页&移动应用支付宝文档中心https://opendocs.alipay.com/open/02no47 demo下载 网页…...
数据库必知必会:TiDB(11)TiDB集群安装
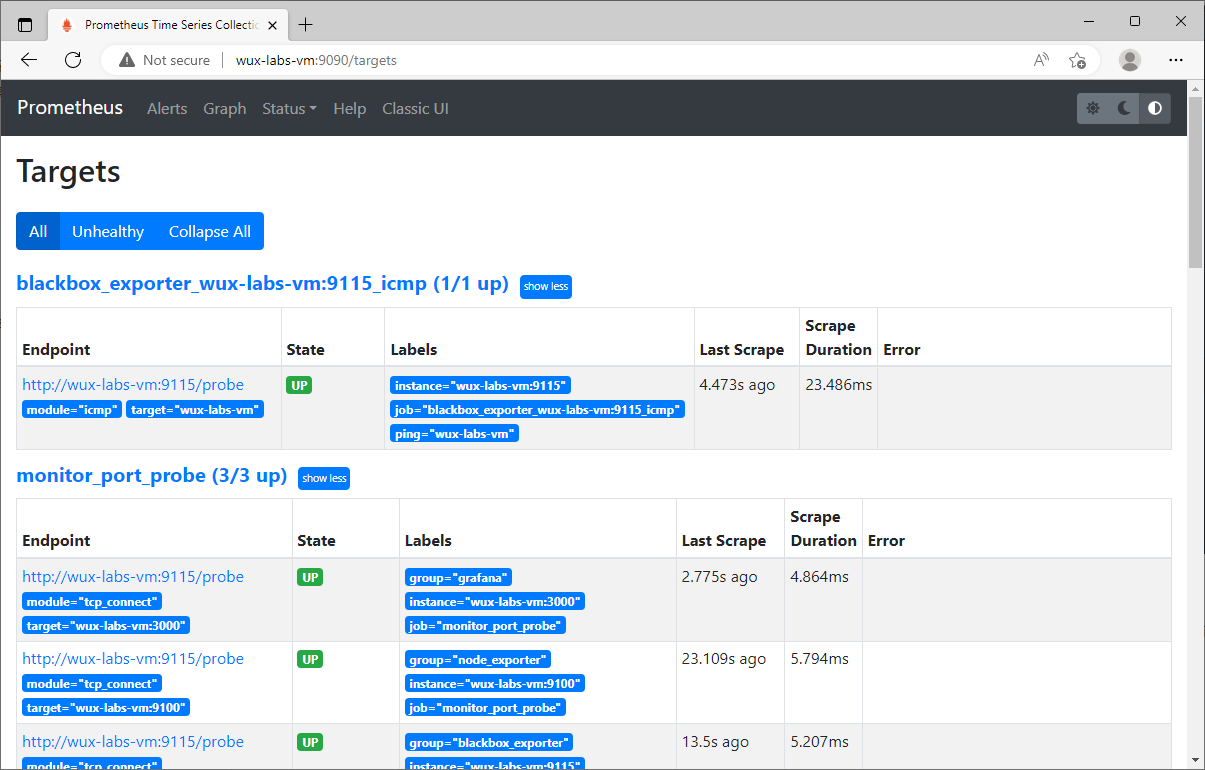
数据库必知必会:TiDB(11)TiDB集群安装TiDB集群安装单机环境上安装集群下载并安装TiUP工具安装TiUP cluster组件创建拓扑文件配置SSH免密登录检查安装要求创建安装目录部署集群启动集群验证集群启动使用命令验证通过Dashboard查看通过Grafana查…...
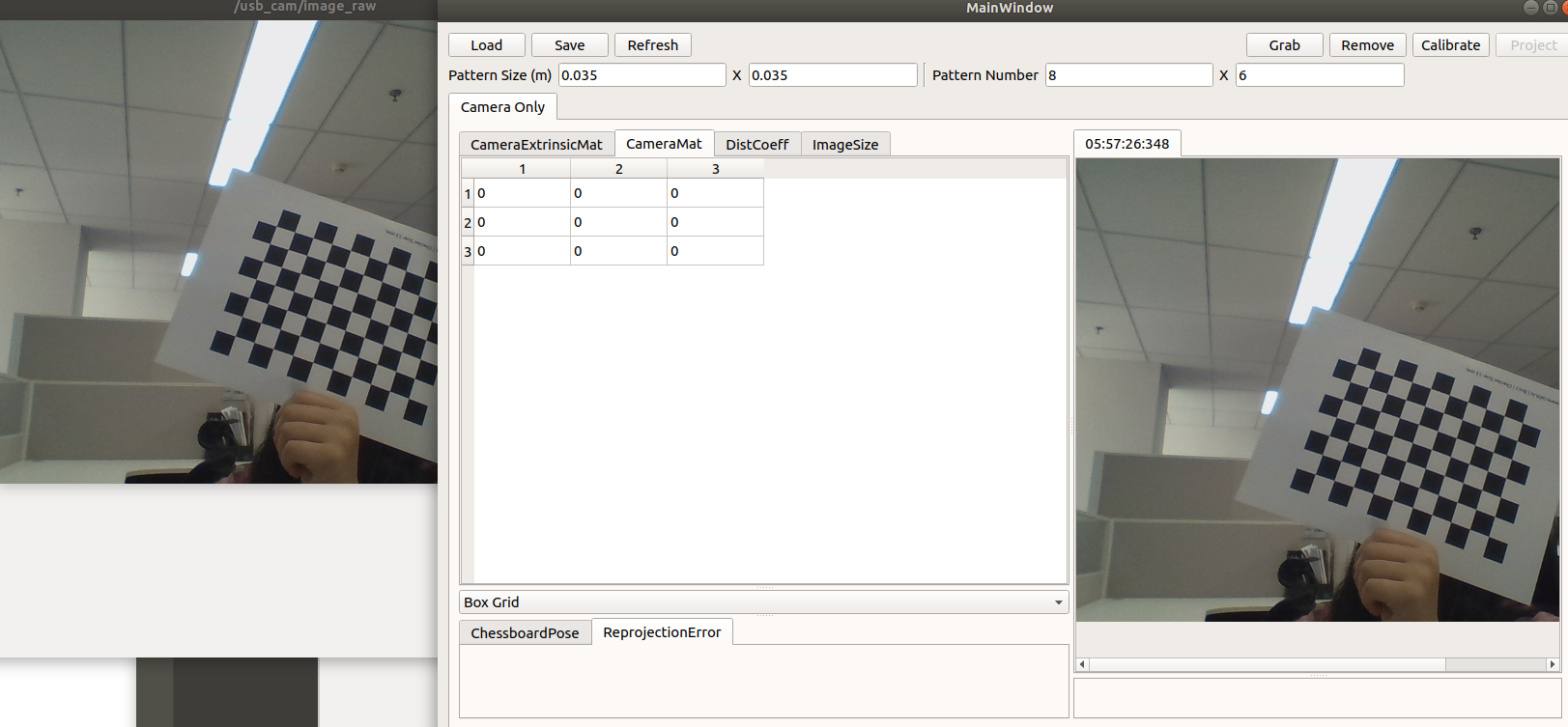
ubuntu18安装Autoware 标定工具箱
参考链接:https://blog.csdn.net/zbr794866300/article/details/107109186#:~:textAutoware1.10%E4%BB%A5%E4%B8%8A%E7%9A%84%E8%BD%AF%E4%BB%B6%E9%83%BD%E9%9C%80%E8%A6%81%E5%8D%95%E7%8B%AC%E5%AE%89%E8%A3%85%E8%BF%99%E4%B8%AAcalibration%E6%A0%87%E5%AE%9A%…...

【面试题】ES6 如何将 Set 转化为数组
大厂面试题分享 面试题库后端面试题库 (面试必备) 推荐:★★★★★地址:前端面试题库Set 是 ES6 中新增的一种集合类型,类似于数组,但其成员的值是唯一的,即不会重复。关于Set,可以阅…...

vs2022 实现无线调试安卓(Windows)
文章目录VS安装安卓调试环境前提条件Android SDK 版本查看安卓开启无线调试开启开发者模式打开USB调试功能打开无线调试功能查看配对信息(再次点击无限调试,不是switch开关)准备电脑端输入adb命令配对安卓查看设备清单如果没有设备VS无线调试…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...

【免费数据】2005-2019年我国272个地级市的旅游竞争力多指标数据(33个指标)
旅游业是一个城市的重要产业构成。旅游竞争力是一个城市竞争力的重要构成部分。一个城市的旅游竞争力反映了其在旅游市场竞争中的比较优势。 今日我们分享的是2005-2019年我国272个地级市的旅游竞争力多指标数据!该数据集源自2025年4月发表于《地理学报》的论文成果…...

React核心概念:State是什么?如何用useState管理组件自己的数据?
系列回顾: 在上一篇《React入门第一步》中,我们已经成功创建并运行了第一个React项目。我们学会了用Vite初始化项目,并修改了App.jsx组件,让页面显示出我们想要的文字。但是,那个页面是“死”的,它只是静态…...

小智AI+MCP
什么是小智AI和MCP 如果还不清楚的先看往期文章 手搓小智AI聊天机器人 MCP 深度解析:AI 的USB接口 如何使用小智MCP 1.刷支持mcp的小智固件 2.下载官方MCP的示例代码 Github:https://github.com/78/mcp-calculator 安这个步骤执行 其中MCP_ENDPOI…...

Java中栈的多种实现类详解
Java中栈的多种实现类详解:Stack、LinkedList与ArrayDeque全方位对比 前言一、Stack类——Java最早的栈实现1.1 Stack类简介1.2 常用方法1.3 优缺点分析 二、LinkedList类——灵活的双端链表2.1 LinkedList类简介2.2 常用方法2.3 优缺点分析 三、ArrayDeque类——高…...

