卷积网络与全连接网络的区别
问题
卷积神经网络是一类包含卷积计算且具有深度结构的前馈神经网络,是深度学习。卷积神经网络具有表征学习能力,能够按其阶层结构对输入信息进行平移不变分类,因此也被称为“平移不变人工神经网络。
全连接神经网络是具有多层感知器的的网络,也就是多层神经元的网络。层与层之间需要包括一个非线性激活函数,需要有一个对输入和输出都隐藏的层,还需要保持高度的连通性,由网络的突触权重决定。那两者的区别是什么呢?
方法
卷积神经网络也是通过一层一层的节点组织起来的。和全连接神经网络一样,卷积神经网络中的每一个节点就是一个神经元。在全连接神经网络中,每相邻两层之间的节点都有边相连,于是会将每一层的全连接层中的节点组织成一列,这样方便显示连接结构。而对于卷积神经网络,相邻两层之间只有部分节点相连,为了展示每一层神经元的维度,一般会将每一层卷积层的节点组织成一个三维矩阵。
除了结构相似,卷积神经网络的输入输出以及训练的流程和全连接神经网络也基本一致,以图像分类为列,卷积神经网络的输入层就是图像的原始图像,而输出层中的每一个节点代表了不同类别的可信度。这和全连接神经网络的输入输出是一致的。类似的,全连接神经网络的损失函数以及参数的优化过程也都适用于卷积神经网络。因此,全连接神经网络和卷积神经网络的唯一区别就是神经网络相邻两层的连接方式。
但是全神经网络无法很好地处理好图像数据,然而卷积神经网络却很好地客服了这个缺点,使用全连接神经网络处理图像的最大问题就是:全连接层的参数太多,对于MNIST数据,每一张图片的大小是28*28*1,其中28*28代表的是图片的大小,*1表示图像是黑白的,有一个色彩通道。假设第一层隐藏层的节点数为500个,那么一个全连接层的神经网络有28*28*500+500=392500个参数,而且有的图片会更大或者是彩色的图片,这时候参数将会更多。参数增多除了导致计算速度减慢,还很容易导致过拟合的问题。所以需要一个合理的神经网络结构来有效的减少神经网络中参数的个数。卷积神经网络就可以更好的达到这个目的。
| from keras import layers from keras import models from keras.datasets import mnist from keras.utils import to_categorical (train_images, train_labels), (test_images, test_labels) = mnist.load_data('D:/Python36/Coding/PycharmProjects/ttt/mnist.npz') train_images = train_images.reshape(60000, 28*28) train_images = train_images.astype('float32') / 255 test_images = test_images.reshape(10000, 28*28) test_images = test_images.astype('float32') / 255 train_labels = to_categorical(train_labels) test_labels = to_categorical(test_labels) model = models.Sequential() model.add(layers.Dense(512, activation='relu', input_shape=(28 * 28,))) model.add(layers.Dense(10, activation='softmax')) model.compile(optimizer='rmsprop',loss='categorical_crossentropy',metrics=['accuracy']) history=model.fit(train_images, train_labels, epochs=10, batch_size=128) test_loss, test_acc = model.evaluate(test_images, test_labels) print(test_acc,test_acc) #0.9786 0.9786 print("history_dict%s =" %history.history) #history_dict = {'loss': [0.25715254720052083, 0.1041663886765639, 0.06873120647072792, 0.049757948418458306, 0.037821156319851675, 0.02870141142855088, 0.02186925242592891, 0.01737390520994862, 0.01316443470219771, 0.010196967865650853], # 'acc': [0.9253666666984558, 0.9694833333333334, 0.9794666666348775, 0.9850166666984558, 0.9886666666666667, 0.9917666666666667, 0.9935499999682108, 0.9949499999682109, 0.9960999999682109, 0.9972833333333333]} = acc1 = history.history['acc'] loss1 = history.history['loss'] print(model.summary()) (train_images, train_labels), (test_images, test_labels) = mnist.load_data('D:/Python36/Coding/PycharmProjects/ttt/mnist.npz') train_images = train_images.reshape((60000, 28, 28, 1)) train_images = train_images.astype('float32') / 255 test_images = test_images.reshape((10000, 28, 28, 1)) test_images = test_images.astype('float32') / 255 train_labels = to_categorical(train_labels) test_labels = to_categorical(test_labels) model = models.Sequential() model.add(layers.Conv2D(32, (3, 3), activation='relu', input_shape=(28, 28, 1))) model.add(layers.MaxPooling2D((2, 2))) model.add(layers.Conv2D(64, (3, 3), activation='relu')) model.add(layers.MaxPooling2D((2, 2))) model.add(layers.Conv2D(64, (3, 3), activation='relu')) model.add(layers.Flatten()) model.add(layers.Dense(64, activation='relu')) model.add(layers.Dense(10, activation='softmax')) model.compile(optimizer='rmsprop',loss='categorical_crossentropy',metrics=['accuracy']) history = model.fit(train_images, train_labels, epochs=10, batch_size=64) test_loss, test_acc = model.evaluate(test_images, test_labels) ##0.9919 0.9919 print("history_dict =%s" %history.history) #history_dict = {'loss': [0.1729982195024689, 0.04632370648694535, 0.031306330454613396, 0.02327785180026355, 0.01820601755216679, 0.01537780981725761, 0.011968255878429288, 0.010757189085084126, 0.008755202058390447, 0.007045005079609898], # 'acc': [0.9456333333333333, 0.9859, 0.9903333333333333, 0.9929333333333333, 0.99435, 0.9953333333333333, 0.9962333333333333, 0.9966, 0.99735, 0.9979333333333333]} acc2 = history.history['acc'] loss2 = history.history['loss'] print(model.summary()) import matplotlib.pyplot as plt fig=plt.figure() ax=fig.add_subplot(1,1,1) epochs = range(1, len(acc1) + 1) ax.plot(epochs, acc1, 'bo', label='dense Training acc',color='red') ax.plot(epochs, loss1, 'b', label='dense Training loss',color='red') ax.plot(epochs, acc2, 'bo', label='Conv2D Training acc',color='green') ax.plot(epochs, loss2, 'b', label='Conv2D Training loss',color='green') ax.legend(loc='best') ax.set_title('Training and validation accuracy by different model') ax.set_xlabel('Epochs') ax.set_ylabel('Accuracy') plt.show() 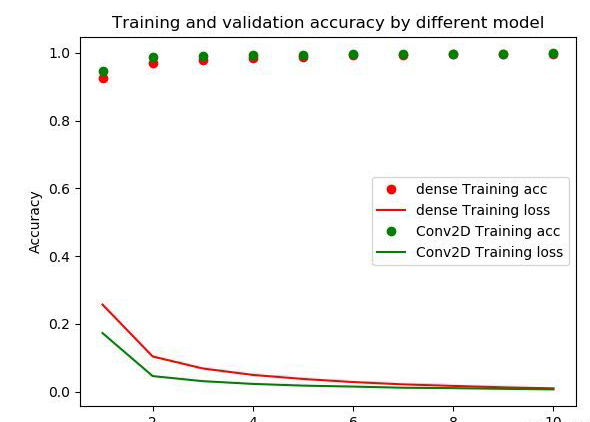 |
结语
全连接网络没有卷积层,只使用全连接层(以及非线性层)。
以关键是理解卷积层和全连接层的区别。
全连接层有三个特点:
关注全局信息(每个点都和前后层的所有点链接)
参数量巨大,计算耗时
输入维度需要匹配(因为是矩阵运算,维度不一致无法计算)
卷积层
这个卷积和信号系统中的卷积不太一样,其实就是一个简单的乘加运算,
局部链接:当前层的神经元只和下一层神经元的局部链接(并不是全连接层的全局链接)
权重共享:神经元的参数(如上图的3*3卷积核),在整个特征图上都是共享的,而不是每个滑动窗口都不同
也正是因为这两个特性,所以卷积层相比于全连接层有如下优点:
需要学习的参数更少,从而降低了过度拟合的可能性,因为该模型不如完全连接的网络复杂。
只需要考虑中的上下文/共享信息。这个未来在许多应用中非常重要,例如图像、视频、文本和语音处理/挖掘,因为相邻输入(例如像素、帧、单词等)通常携带相关信息。
但需要注意的是,无论是全连接层,还是卷积层,都是线性层,只能拟合线性函数,所以都需要通过ReLU等引入非线性,以增加模型的表达能力。比如ReLU函数接受一个输入x,并返回{0, x}的最大值。ReLU(x) = argmax(x, 0)。
相关文章:

卷积网络与全连接网络的区别
问题卷积神经网络是一类包含卷积计算且具有深度结构的前馈神经网络,是深度学习。卷积神经网络具有表征学习能力,能够按其阶层结构对输入信息进行平移不变分类,因此也被称为“平移不变人工神经网络。全连接神经网络是具有多层感知器的的网络&a…...

【5000左右电脑配置清单】预算不高于5000,不带显示器的电脑配置清单推荐
由于本人是学生党经济有限,预算不高于5000元配一套电脑主机,说实话5000左右的电脑配置已经很好了,今天站长整理了几款配置给大家参考参考,更多电脑配置还请继续关注西安SEO优化站点! 配置1: <CPU> I5…...
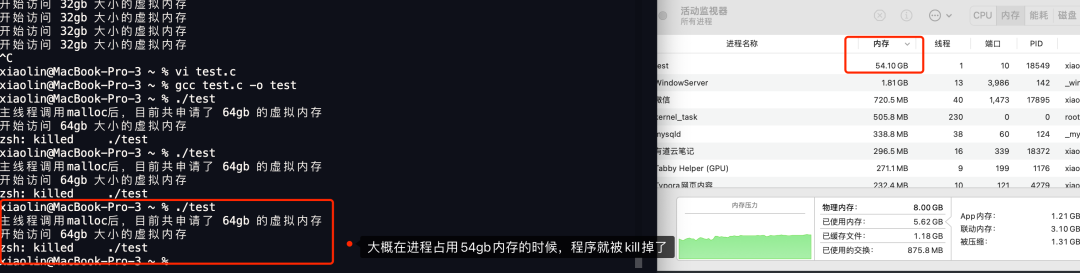
在 4G 内存的机器上,申请 8G 内存会怎么样?
在 4GB 物理内存的机器上,申请 8G 内存会怎么样? 这个问题在没有前置条件下,就说出答案就是耍流氓。这个问题要考虑三个前置条件: 操作系统是 32 位的,还是 64 位的?申请完 8G 内存后会不会被使用&#x…...
JavaSE学习day9 集合(基础班结束)
1.ArrayList 集合和数组的优势对比: 长度可变 添加数据的时候不需要考虑索引,默认将数据添加到末尾 不能存基本数据类型。只能通过包装。 1.1ArrayList类概述 什么是集合 提供一种存储空间可变的存储模型,存储的数据容量可以发生改变 Ar…...
Python爬虫进阶 - win和linux下selenium使用代理
目录 Windows selenium配置 下载地址 Chrome Chromedriver 版本对应关系 实践测试 操作元素 浏览器操作 获取元素信息 鼠标操作 实战demo selenium添加代理 Linux selenium配置 检查服务器环境 下载安装第三方库(最简单版) 实践测试 代码…...

力扣-从不订购的客户
大家好,我是空空star,本篇带大家了解一道简单的力扣sql练习题。 文章目录前言一、题目:183. 从不订购的客户二、解题1.正确示范①提交SQL运行结果2.正确示范②提交SQL运行结果3.正确示范③提交SQL运行结果4.正确示范④提交SQL运行结果总结前言…...

速来!掘金数据时代2022年度隐私计算评选活动火热报名中!
开放隐私计算 开放隐私计算开放隐私计算OpenMPC是国内第一个且影响力最大的隐私计算开放社区。社区秉承开放共享的精神,专注于隐私计算行业的研究与布道。社区致力于隐私计算技术的传播,愿成为中国 “隐私计算最后一公里的服务区”。183篇原创内容公众号…...

Springboot @Test 给Controller接口 写 单元测试
前言 最近有小伙伴问到怎么给 controller的接口写单元测试。 单元测试是开发必不可少的一个环节。 既然有人问到了,那我觉得可能不止一个人不会,那就按照惯例,出手。 正文 内容: 主要是get 和 post 两种请求方式的接口 的 单元测…...

ISO 6721-1~12 ,塑料-电动机械性能的测定,2022更新
ISO 6721-1 :2019 Plastics - Determination of dynamic mechanical properties - Part 1: General principles ISO 6721-1 :2019 塑料 - 电动机械性能的测定. 第1部分:一般原理 ISO 6721-2 :2019 Plastics — Determination of dynamic mechanical properties — Part 2:…...

vue3.2中使用swiper缩略图轮播教程
介绍 在vue3 中使用 swiper 实现缩略图的轮播图效果,具体如下图所示: 使用 切换到项目终端 ,输入命令 npm install swiper --save , 进行安装在 main.js里,引入 swiper.css并使用,具体代码如下;import {createApp } from vue import App from ./App.vue import router…...

边玩边学,13个 Python 小游戏真有趣啊(含源码)
经常听到有朋友说,学习编程是一件非常枯燥无味的事情。其实,大家有没有认真想过,可能是我们的学习方法不对? 比方说,你有没有想过,可以通过打游戏来学编程? 今天我想跟大家分享几个Python小游…...
)
MySQL数据文件迁移(不关闭SELinux)
背景 日常实施中可能会出现在部署MySQL时未更改数据默认存储路径(默认:/var/lib/mysql),然而一般分配服务器的人只会给系统分区分配50G的空间,这导致后续空间不够用的情况,也就出现了需要迁移数据的问题。…...
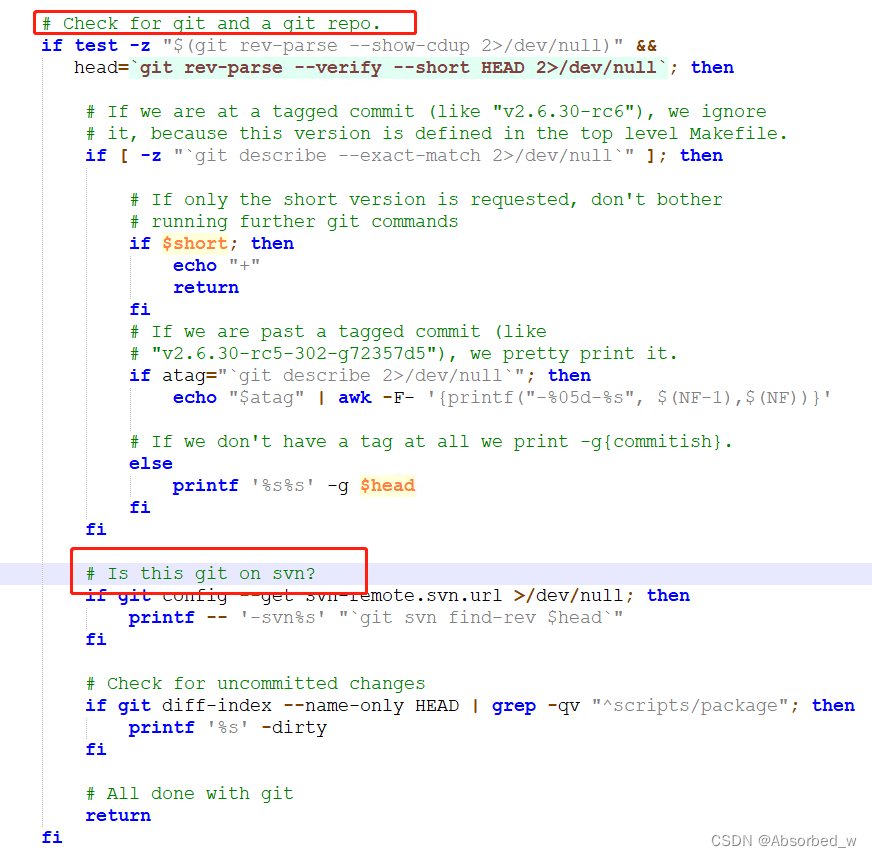
uboot / linux添加/去除 版本号LOCALVERSION
背景 偶然的机会,在insmod驱动模块的时候,遇到报错: 查找原因,说是当前系统内核版本和模块编译使用版本不同! 使用如下命令查看当前系统内核版本: uname -r 使用modinfo命令(嵌入式设备没有此…...

2023北京养老展,北京养老展会,北京养老产业展览会
CBIAIE第十届中国(北京)国际老年产业博览会,8月28-30日在北京亦创国际会展中心举办; 预期效果:中国(北京)国际老年产业博览会China (Beijing) International Aged industry Expo(CB…...

华为OD机试 - 分糖果(Java) | 机试题算法思路 【2023】
使用说明 参加华为od机试,一定要注意不要完全背诵代码,需要理解之后模仿写出,通过率才会高。 华为 OD 清单查看地址:https://blog.csdn.net/hihell/category_12201821.html 华为OD详细说明:https://dream.blog.csdn.net/article/details/128980730 分糖果 小明从糖果…...

带你彻底了解浮点型数据的存储
🚀🚀🚀大家觉不错的话,就恳求大家点点关注,点点小爱心,指点指点🚀🚀🚀 目录 🐰浮点型在内存的存储 🤔提示:数据类型的存储范围 &a…...

【牛客刷题专栏】0x0C:JZ4 二维数组中的查找(C语言编程题)
前言 个人推荐在牛客网刷题(点击可以跳转),它登陆后会保存刷题记录进度,重新登录时写过的题目代码不会丢失。个人刷题练习系列专栏:个人CSDN牛客刷题专栏。 题目来自:牛客/题库 / 在线编程 / 剑指offer: 目录前言问题…...
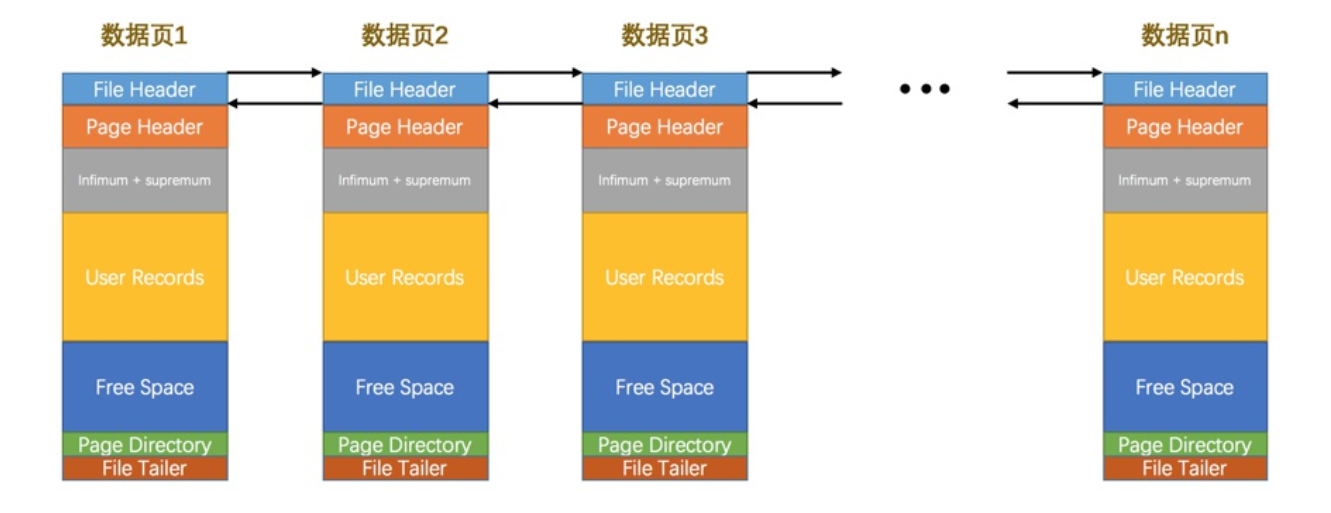
「mysql是怎样运行的」第5章 盛放记录的大盒子---InnoDB数据页结构
「mysql是怎样运行的」第五章 盛放记录的大盒子—InnoDB数据页结构 文章目录「mysql是怎样运行的」第五章 盛放记录的大盒子---InnoDB数据页结构[toc]一、不同类型的页介绍二、数据页结构的快速浏览三、记录在页中的存储记录头信息的秘密四、Page Directory(页目录)五、Page He…...
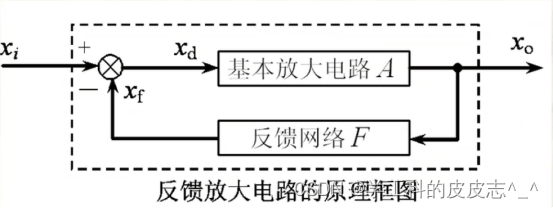
模电中的负反馈
文章目录一、反馈是什么?二、负反馈对于放大性能的影响1.负反馈的作用三、正反馈总结– 一、反馈是什么? 反馈的定义:凡是将放大电路输出端信号(电压或电流)的一部分或者全部引回到输入端,与输入信号叠加…...
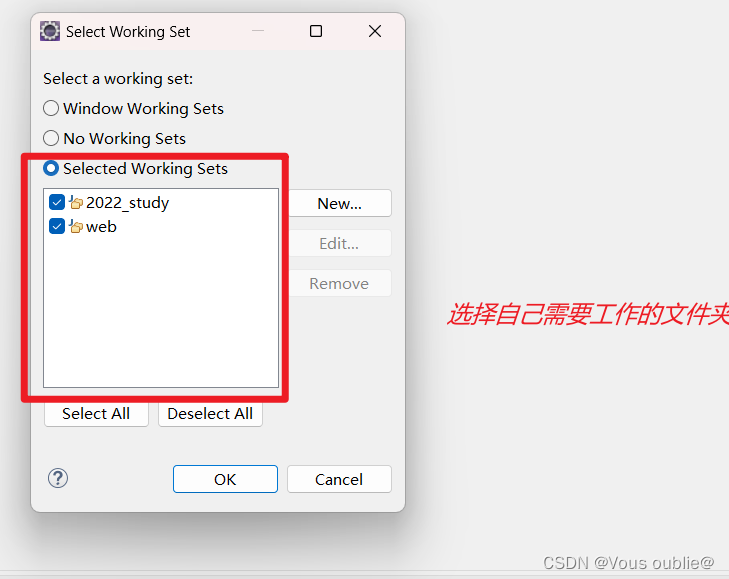
eclipse中整理左侧项目栏文件
💡在使用eclipse的过程中,随着项目越来越多,会使得项目管理变得困难,介绍一下eclipse中对于项目分类存放(Java Working Set)的解决方案。如果按照默认的方式查看项目列表是这种效果:⭕当创建使用小项目过多…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...
)
LLaMA-Factory 微调 Qwen2-VL 进行人脸情感识别(二)
在上一篇文章中,我们详细介绍了如何使用LLaMA-Factory框架对Qwen2-VL大模型进行微调,以实现人脸情感识别的功能。本篇文章将聚焦于微调完成后,如何调用这个模型进行人脸情感识别的具体代码实现,包括详细的步骤和注释。 模型调用步骤 环境准备:确保安装了必要的Python库。…...

【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅!
【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅! 🌱 前言:一棵树的浪漫,从数组开始说起 程序员的世界里,数组是最常见的基本结构之一,几乎每种语言、每种算法都少不了它。可你有没有想过,一组看似“线性排列”的有序数组,竟然可以**“长”成一棵平衡的二…...
之(六) ——通用对象池总结(核心))
怎么开发一个网络协议模块(C语言框架)之(六) ——通用对象池总结(核心)
+---------------------------+ | operEntryTbl[] | ← 操作对象池 (对象数组) +---------------------------+ | 0 | 1 | 2 | ... | N-1 | +---------------------------+↓ 初始化时全部加入 +------------------------+ +-------------------------+ | …...

【版本控制】GitHub Desktop 入门教程与开源协作全流程解析
目录 0 引言1 GitHub Desktop 入门教程1.1 安装与基础配置1.2 核心功能使用指南仓库管理日常开发流程分支管理 2 GitHub 开源协作流程详解2.1 Fork & Pull Request 模型2.2 完整协作流程步骤步骤 1: Fork(创建个人副本)步骤 2: Clone(克隆…...

RKNN开发环境搭建2-RKNN Model Zoo 环境搭建
目录 1.简介2.环境搭建2.1 启动 docker 环境2.2 安装依赖工具2.3 下载 RKNN Model Zoo2.4 RKNN模型转化2.5编译C++1.简介 RKNN Model Zoo基于 RKNPU SDK 工具链开发, 提供了目前主流算法的部署例程. 例程包含导出RKNN模型, 使用 Python API, CAPI 推理 RKNN 模型的流程. 本…...

十二、【ESP32全栈开发指南: IDF开发环境下cJSON使用】
一、JSON简介 JSON(JavaScript Object Notation)是一种轻量级的数据交换格式,具有以下核心特性: 完全独立于编程语言的文本格式易于人阅读和编写易于机器解析和生成基于ECMAScript标准子集 1.1 JSON语法规则 {"name"…...

qt 双缓冲案例对比
双缓冲 1.双缓冲原理 单缓冲:在paintEvent中直接绘制到屏幕,绘制过程被用户看到 双缓冲:先在redrawBuffer绘制到缓冲区,然后一次性显示完整结果 代码结构 单缓冲:所有绘制逻辑在paintEvent中 双缓冲:绘制…...

Caliper 配置文件解析:config.yaml 和 fisco-bcos.json 附加在caliper中执行不同的合约方法
Caliper 配置文件解析:config.yaml 和 fisco-bcos.json Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO…...
