单调队列
目录
一,单调队列
二,模板实现
三,OJ实战
剑指 Offer 59 - I. 滑动窗口的最大值
一,单调队列
单调队列是双端队列的拓展,支持尾部插入,双端删除,其中的数据始终维持单调性,从而队首就是所需的最值信息。
和单调栈类似,单调队列用于处理一个数组,扫描数组时,依次尾部插入一个数。
尾部插入过程中,为了维持单调性,可能需要先执行尾部删除(对应强制单调栈)。
而队首的删除操作,由外部决定调用时机。
二,模板实现
//单调队列
class MonotonicQueue {
public:MonotonicQueue(int type) { //0递增队列,队首最小,1递减队列,队首最大this->type = type;id = 0;}void push_back(int x) {while (!q.empty() && (type ? (m[q.back()] < x) : (m[q.back()] > x)))q.pop_back();q.push_back(id);m[id++] = x;}void pop_front() {if (!q.empty())q.pop_front();}void pop_back() {if (!q.empty())q.pop_back();}int frontId() {return q.front();}int front() {return m[q.front()];}int tailId() {return q.back();}int size() {return q.size();}
private:deque<int>q;map<int, int>m;int type, id;
};三,OJ实战
剑指 Offer 59 - I. 滑动窗口的最大值
题目:
给定一个数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回滑动窗口中的最大值。
进阶:
你能在线性时间复杂度内解决此题吗?
示例:
输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3
输出: [3,3,5,5,6,7]
解释:
滑动窗口的位置 最大值
--------------- -----
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7
提示:
1 <= nums.length <= 10^5
-10^4 <= nums[i] <= 10^4
1 <= k <= nums.length
思路一:
线段树
class SegmentTree<2> opt;class Solution {
public:vector<int> maxSlidingWindow(vector<int>& nums, int k) {int n = nums.size();for (int i = 0; i < n; i++)*(opt.getData() + i + 1) = nums[i];opt.build(n);vector<int>ans;ans.resize(n - k + 1);for (int i = 0; i < ans.size(); i++)ans[i] = opt.query(i + 1, i + k);return ans;}
};思路二:
单调队列
class Solution {
public:vector<int> maxSlidingWindow(vector<int>& nums, int k) {vector<int>ans;MonotonicQueue q(1);for (int i = 0; i < k; i++)q.push_back(nums[i]);for (int i = k; i < nums.size(); i++) {ans.push_back(q.front());q.push_back(nums[i]);if (q.tailId() - k == q.frontId())q.pop_front();}ans.push_back(q.front());return ans;}
};相关文章:

单调队列
目录 一,单调队列 二,模板实现 三,OJ实战 剑指 Offer 59 - I. 滑动窗口的最大值 一,单调队列 单调队列是双端队列的拓展,支持尾部插入,双端删除,其中的数据始终维持单调性,从而…...

effective c++ 笔记
TODO:还没看太懂的篇章 item25 item35 模板相关内容 文章目录 基础视C为一个语言联邦以const, enum, inline替换#define尽可能使用constconst成员函数 确定对象使用前已被初始化 构造、析构和赋值内含引用或常量成员的类的赋值操作需要自己重写不想使用自动生成的函…...

【送书活动】深入浅出SSD:固态存储核心技术、原理与实战
前言 「作者主页」:雪碧有白泡泡 「个人网站」:雪碧的个人网站 「推荐专栏」: ★java一站式服务 ★ ★ React从入门到精通★ ★前端炫酷代码分享 ★ ★ 从0到英雄,vue成神之路★ ★ uniapp-从构建到提升★ ★ 从0到英雄ÿ…...
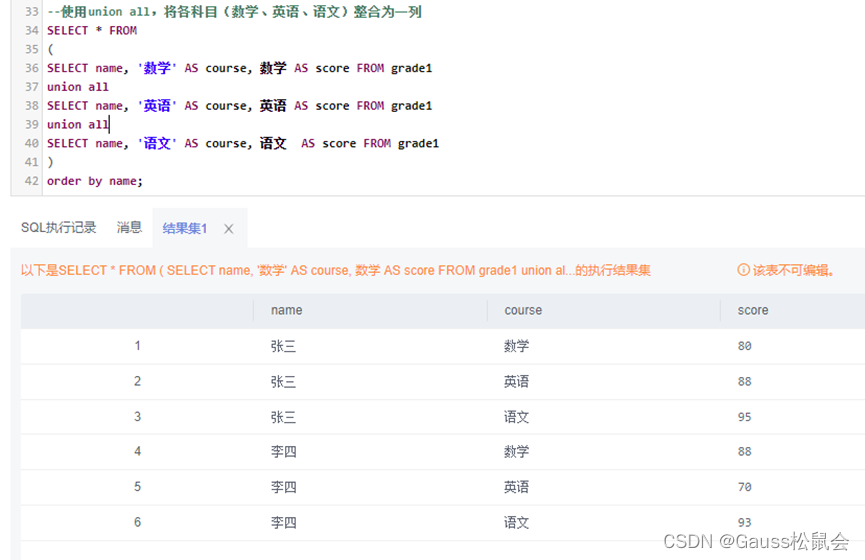
GaussDB数据库SQL系列-行列转换
一、前言 二、简述 1、行转列概念 2、列转行概念 三、GaussDB数据库的行列转行实验示例 1、行转列示例 1)创建实验表(行存表) 2)静态行转列 3)行转列(结果值:拼接式) 4&…...

美国陆军网络司令部利用人工智能增强网络攻防和作战决策能力
源自: 奇安网情局 声明:公众号转载的文章及图片出于非商业性的教育和科研目的供大家参考和探讨,并不意味着支持其观点或证实其内容的真实性。版权归原作者所有,如转载稿涉及版权等问题,请立即联系我们删除。 “人工智能技术与咨询…...

Notion团队协作魔法:如何玩转数字工作空间?
Notion简介 Notion已经成为现代团队协作的首选工具之一。它不仅仅是一个笔记应用,更是一个强大的团队协作平台,能够满足多种工作场景的需求。 Notion的核心功能 Notion提供了丰富的功能,如文档、数据库、看板、日历等,满足团队的…...

视频云存储/安防监控/AI视频智能分析平台新功能:人员倒地检测详解
人工智能技术已经越来越多地融入到视频监控领域中,近期我们也发布了基于AI智能视频云存储/安防监控视频智能分析平台的众多新功能,该平台内置多种AI算法,可对实时视频中的人脸、人体、物体等进行检测、跟踪与抓拍,支持口罩佩戴检测…...

解决RabbitMQ报错Stats in management UI are disabled on this node
文章目录 问题描述:解决步骤:进入容器后,cd到以下路径修改 management_agent.disable_metrics_collector false退出容器重启rabbitmq容器 问题描述: linux 部署 rabbitmq后,打开rabbitmq管理界面。点击channels&#…...

【重点】【NAND】聊聊固态硬盘SSD的寿命及其影响因素
固态硬盘是由主控芯片、存储颗粒芯片组成的闪存设备,固体硬盘的英文简称是SSD,如果是移动用的固态硬盘,则其英文简称为PSSD。 固态硬盘SSD分工业级和消费级等,目前,工业级固态硬盘SSD通常采用MLC闪存,而消…...

数据库约束
文章目录 1. 简介2. 代码演示3. 外键约束4. 外键删除和更新行为 1. 简介 概念:约束时作用于表中子段上的规则,用于限制存储在表中的shuju目的:保证数据库中数据的正确、有效性和完整性分类: 约束描述关键字非空约束限制该字段不…...

Unity实现MQTT服务器
首先下载MqttNet:MqttNet下载地址 解压好后使用vs打开,并生成.dll文件(我这里下载的是4.1.2.350版本) 然后再/Source/MQTTnet/bin/Debug/net452 文件夹中找到生成的文件 新建unity工程,创建Plugins文件夹࿰…...

Linux(centos) 下 Mysql 环境安装
linux 下进行环境安装相对比较简单,可还是会遇到各种奇奇怪怪的问题,我们来梳理一波 安装 mysql 我们会用到下地址: Mysql 官方文档的地址,可以参考,不要全部使用 https://dev.mysql.com/doc/refman/8.0/en/linux-i…...
决策树(Decision Tree)
决策树的定义: 分类决策树模型是一种描述对实例进行分类的树形结构。决策树由结点(node)和有向边(directed edge)组成。结点有两种类型: 内部结点(internal node)和叶结点(leaf node࿰…...

解决 PaddleClas 下载预训练模型报错 ModuleNotFoundError No module named ‘ppcls‘ 的问题
当我们在使用 PaddleClas 进行预训练模型下载时,可能会遇到一个报错,报错信息为 ModuleNotFoundError: No module named ppcls。这个错误通常是因为 Python 解释器无法找到名为 ppcls 的模块,而我们的代码中正尝试导入它。让我们一起来解决这…...
视觉化洞察:为什么我们需要数据可视化?
为什么我们需要数据可视化?这个问题在信息时代变得愈发重要。数据,如今已成为生活的一部分,我们每天都在产生大量的数据,从社交媒体到购物记录,从健康数据到工作表现,数据无处不在。然而,数据本…...

C语言函数概述——拜佛代码
函数是一种可重用的代码块,用于执行特定任务或完成特定功能函数作用:对具备相同逻辑的代码进行封装,提高代码的编写效率,实现对代码的重用函数作用演示代码: #include <stdio.h>// 定义函数 void func() {print…...

防火墙日志分析工具
防火墙提供对进入组织网络的网络流量的来源和类型的可见性,这使得防火墙日志成为重要的信息源,包括所有连接的源地址、目标地址、协议和端口号等详细信息,此信息可以提供对未知安全威胁的见解,是威胁管理中的重要工具。 防火墙日…...

Autofac中多个类继承同一个接口,如何注入?与抽象工厂模式相结合
多个类继承同一个接口,如何注入?与抽象工厂模式相结合 需求: 原来是抽象工厂模式,多个类继承同一个接口。 现在需要使用Autofac进行选择性注入。 Autofac默认常识: Autofac中多个类继承同一个接口,默认是最后一个接口注入的类。 解决方案:(约定大于配…...

Django系列之日志配置
如何配置 settings.py 文件中增加如下日志模块 """logger 配置""" LOGGING {version: 1,disable_existing_loggers: False, # 是否去掉目前项目中其他地方中以及使用的日志功能,但是将来我们可能会引入第三方的模块,里…...

四轴飞行器传感器(SimulinkMatlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...

Spring Boot + MyBatis 集成支付宝支付流程
Spring Boot MyBatis 集成支付宝支付流程 核心流程 商户系统生成订单调用支付宝创建预支付订单用户跳转支付宝完成支付支付宝异步通知支付结果商户处理支付结果更新订单状态支付宝同步跳转回商户页面 代码实现示例(电脑网站支付) 1. 添加依赖 <!…...
