决策树(Decision Tree)
决策树的定义:
分类决策树模型是一种描述对实例进行分类的树形结构。决策树由结点(node)和有向边(directed edge)组成。结点有两种类型: 内部结点(internal node)和叶结点(leaf node)。内部结点表示一个特征或属性(features),叶结点表示一个类(labels)。
用决策树对需要测试的实例进行分类: 从根节点开始,对实例的某一特征进行测试,根据测试结果,将实例分配到其子结点;这时,每一个子结点对应着该特征的一个取值。如此递归地对实例进行测试并分配,直至达到叶结点。最后将实例分配到叶结点的类中。
每次寻找最优的特征列,那么该如何找到呢,使用的是香农熵:
代表随机事件x的概率
信息量是对信息的度量,就跟时间的度量是秒一样,当我们考虑一个离散的随机变量 x 的时候,当我们观察到的这个变量的一个具体值的时候,我们接收到了多少信息呢?
多少信息用信息量来衡量,我们接受到的信息量跟具体发生的事件有关。
信息的大小跟随机事件的概率有关。越小概率的事情发生了产生的信息量越大,如湖南产生 的地震了;越大概率的事情发生了产生的信息量越小,如太阳从东边升起来了(肯定发生嘛, 没什么信息量)。因此一个具体事件的信息量应该是随着其发生概率而递减的,且不能为负。
假如有两个不相关事件,x和y,两个事件同时发生时获得的信息应该等于观察到的事件各自发生时获得的信息之和,即:h(x,y)=h(x)+h(y)
而两个事件同时发生的概率为p(x,y)=p(x)*p(y)
这里就可以看出h(x,y)和p(x,y)的关系为对数关系
h(x,y)=log(p(x,y))=log(p(x))+log(p(y))
所以 (log是以2为底)
前面加个负号是因为信息量为正数
信息熵 下面正式引出信息熵:信息量度量的是一个具体事件发生了所带来的信息,而熵则是在结果出来之前对可能产生的信息量的期望——考虑该随机变量的所有可能取值,即所有可能发生事件所带来的信息量的期望。即
信息熵还可以作为一个系统复杂程度的度量,如果系统越复杂,出现不同情况的种类越多, 那么他的信息熵是比较大的。如果一个系统越简单,出现情况种类很少(极端情况为 1 种情况,那么对应概率为 1,那么对应的信息熵为 0),此时的信息熵较小。
例子:
数据集:
1.5 50 thin
1.5 60 fat
1.6 40 thin
1.6 60 fat
1.7 60 thin
1.7 80 fat
1.8 60 thin
1.8 90 fat
1.9 70 thin
1.9 80 thin
第一列身高,第二列体重,第三列label
首先,对两列特征值分别进行计算,从第一列开始,以1.5为特征值划分数据集为
50 thin
60 fat
计算香农熵:
然后再以1.6划分:
。。。。
第一列划分完再把这一列香农熵加起来,再划分第二列,同第一列步骤一致,加起来后和第一列比较,找到香农熵最小的feature列分类。
下一层树再以同样的方式进行分类。
from numpy import *
from __future__ import print_function
import operator
from os import listdir
from collections import Counter
import matplotlib
import matplotlib.pyplot as plt
import mathdef createDataSet():dataSet=[[1,1,'yes'],[1,1,'yes'],[1,0,'no'],[0,1,'no'],[0,1,'no']]labels=['no surfacing','flippers']return dataSet,labels#计算香农熵函数
def calcShannonEnt(dataSet):"""calcShannonEnt(calculate Shannon entropy 计算给定数据集的香农熵)Args:dataSet 数据集Returns:返回 每一组feature下的某个分类下,香农熵的信息期望"""# -----------计算香农熵的第一种实现方式start--------------------------------------------------------------------------------# 求list的长度,表示计算参与训练的数据量numEntries = len(dataSet)# 下面输出我们测试的数据集的一些信息# 例如: <type 'list'> numEntries: 5 是下面的代码的输出# print type(dataSet), 'numEntries: ', numEntries# 计算分类标签label出现的次数labelCounts = {}# the the number of unique elements and their occurancefor featVec in dataSet:# 将当前实例的标签存储,即每一行数据的最后一个数据代表的是标签currentLabel = featVec[-1]# 为所有可能的分类创建字典,如果当前的键值不存在,则扩展字典并将当前键值加入字典。每个键值都记录了当前类别出现的次数。if currentLabel not in labelCounts.keys():labelCounts[currentLabel] = 0labelCounts[currentLabel] += 1# print '-----', featVec, labelCounts# 对于label标签的占比,求出label标签的香农熵shannonEnt = 0.0for key in labelCounts:# 使用所有类标签的发生频率计算类别出现的概率。prob = float(labelCounts[key])/numEntries# log base 2 # 计算香农熵,以 2 为底求对数shannonEnt -= prob * math.log(prob, 2)# print '---', prob, prob * log(prob, 2), shannonEnt# -----------计算香农熵的第一种实现方式end--------------------------------------------------------------------------------# # -----------计算香农熵的第二种实现方式start--------------------------------------------------------------------------------# # 统计标签出现的次数# label_count = Counter(data[-1] for data in dataSet)# # 计算概率# probs = [p[1] / len(dataSet) for p in label_count.items()]# # 计算香农熵# shannonEnt = sum([-p * log(p, 2) for p in probs])# # -----------计算香农熵的第二种实现方式end--------------------------------------------------------------------------------return shannonEnt
def splitDataSet(dataSet,index,value):retDataSet=[]for featVec in dataSet:if featVec[index]==value:reducedFeatVec=featVec[:index]'''请百度查询一下: extend和append的区别music_media.append(object) 向列表中添加一个对象objectmusic_media.extend(sequence) 把一个序列seq的内容添加到列表中 (跟 += 在list运用类似, music_media += sequence)1、使用append的时候,是将object看作一个对象,整体打包添加到music_media对象中。2、使用extend的时候,是将sequence看作一个序列,将这个序列和music_media序列合并,并放在其后面。music_media = []music_media.extend([1,2,3])print music_media#结果: #[1, 2, 3]music_media.append([4,5,6])print music_media#结果: #[1, 2, 3, [4, 5, 6]]music_media.extend([7,8,9])print music_media#结果: #[1, 2, 3, [4, 5, 6], 7, 8, 9]'''reducedFeatVec.extend(featVec[index+1:])retDataSet.append(reducedFeatVec)return retDataSet
'''
这块是选择最好的特征列
选取最大的信息熵
gain[信息增益]: 划分数据集前后的信息变化, 获取信息熵最大的值
信息增益是熵的减少或者是数据无序度的减少。最后,比较所有特征中的信息增益,返回最好特征划分的索引值。
'''
def chooseBestFeatureToSplit(dataSet):"""chooseBestFeatureToSplit(选择最好的特征)Args:dataSet 数据集Returns:bestFeature 最优的特征列"""# -----------选择最优特征的第一种方式 start------------------------------------# 求第一行有多少列的 Feature, 最后一列是label列嘛numFeatures = len(dataSet[0]) - 1# label的信息熵baseEntropy = calcShannonEnt(dataSet)# 最优的信息增益值, 和最优的Featurn编号bestInfoGain, bestFeature = 0.0, -1# iterate over all the featuresfor i in range(numFeatures):featList=[example[i] for example in dataSet]'''a=[[1,1,1],[2,1,0]]a1=[a2[1] for a2 in a]print(a1)打印集合列'''#对列元素去重uniqueVals=set(featList)#创建临时的信息熵newEntropy=0.0#遍历某一列的value集合,计算该列的信息熵#遍历当前特征中的所有唯一属性值,对每个唯一属性值划分一次数据集,计算数据集的新熵值,并对所有唯一特征值得到的熵求和for value in uniqueVals:subDataSet=splitDataSet(dataSet,i,value)prob=len(subDataSet)/float(len(dataSet))newEntropy+=prob*calcShannonEnt(subDataSet)infoGain=baseEntropy-newEntropyprint('infoGain=',infoGain,'bestFeature=',i,baseEntropy,newEntropy)if(infoGain>bestInfoGain):bestInfoGain=infoGainbestFeature=ireturn bestFeaturedef majorityCnt(classList):classCount={}for vote in classList:if vote not in classCount.keys():classCount[vote]=0;classCount[vote]+=1;# 倒叙排列classCount得到一个字典集合,然后取出第一个就是结果(yes/no),即出现次数最多的结果sortedClassCount=sorted(classCount.iteritems(),key=operator.itemgetter(1),reverse=True)return sortedClassCount[0][0]
def createTree(dataSet,labels):classList=[example[-1] for example in dataSet]# 如果数据集的最后一列的第一个值出现的次数=整个集合的数量,也就说只有一个类别,就只直接返回结果就行# 第一个停止条件: 所有的类标签完全相同,则直接返回该类标签。# count() 函数是统计括号中的值在list中出现的次数if classList.count(classList[0])==len(classList):return classList[0]if len(dataSet[0])==1:return majorityCnt(classList)# 选择最优的列,得到最优列对应的label含义bestFeat=chooseBestFeatureToSplit(dataSet)bestFeatLabel=labels[bestFeat]#初始化myTree'''a=[[1,1,1],[2,1,0]]a1= ['age', 'prescript', 'astigmatic', 'tearRate']a3=a1[0]a2={a3:{}}a2[a3][1]='1'a2[a3]['2']='1'print(a2)输出{'age': {1: '1', '2': '1'}}'''myTree={bestFeatLabel:{}}# 注: labels列表是可变对象,在PYTHON函数中作为参数时传址引用,能够被全局修改# 所以这行代码导致函数外的同名变量被删除了元素,造成例句无法执行,提示'no surfacing' is not in listdel(labels[bestFeat])# 取出最优列,然后它的branch做分类featValues=[example[bestFeat]for example in dataSet]uniqueVals=set(featValues)for value in uniqueVals:# 求出剩余的标签labelsubLabels=labels[:]# 遍历当前选择特征包含的所有属性值,在每个数据集划分上递归调用函数createTree()myTree[bestFeatLabel][value]=createTree(splitDataSet(dataSet,bestFeat,value),subLabels)return myTree
def classify(inputTree,featLabels,testVec):"""classify(给输入的节点,进行分类)Args:inputTree 决策树模型featLabels Feature标签对应的名称testVec 测试输入的数据Returns:classLabel 分类的结果值,需要映射label才能知道名称"""# 获取tree的根节点对于的key值firstStr=inputTree.keys()[0]# 通过key得到根节点对应的valuesecondDict=inputTree[firstStr]# 判断根节点名称获取根节点在label中的先后顺序,这样就知道输入的testVec怎么开始对照树来做分类featIndex=featLabels.index(firstStr)# 测试数据,找到根节点对应的label位置,也就知道从输入的数据的第几位来开始分类key=testVec[featIndex]valueOfFeat=secondDict[key]print('+++',firstStr,'xxx',secondDict,'---',key,'>>>',valueOfFeat)# 判断分枝是否结束: 判断valueOfFeat是否是dict类型if isinstance(valueOfFeat,dict):classLabel=classify(valueOfFeat,featLabels,testVec)else:classLabel=valueOfFeat#因为最后一列是label列,所以直接返回就行return classLabel
def storeTree(inputTree,filename):import pickle# -------------- 第一种方法 start --------------#fw=open(filename,'wb')#pickle.dump(inputTree,fw)#fw.close()# -------------- 第一种方法 end --------------# -------------- 第二种方法 start --------------with open(filename,'wb') as fw:pickle.dump(inputTree,fw)# -------------- 第二种方法 start --------------
def grabTree(filename):import picklefr=open(filename,'rb')return pickle.load(fr)
def fishTest():# 1.创建数据和结果标签myDat,labels=createDataSet()# print myDat, labels# 计算label分类标签的香农熵# calcShannonEnt(myDat)# # 求第0列 为 1/0的列的数据集【排除第0列】# print '1---', splitDataSet(myDat, 0, 1)# print '0---', splitDataSet(myDat, 0, 0)# # 计算最好的信息增益的列# print chooseBestFeatureToSplit(myDat)import copymyTree=createTree(myDat,copy.deepcopy(labels))print(myTree)#[i,j]表示要取的分支上的节点位置,对应的结果值print(classify(myTree,labels,[1,1]))# 获得树的高度print(get_tree_height(myTree))print(myTree.keys()[0])#画图可视化展现createPlot(myTree)
def get_tree_height(tree):"""Desc:递归获得决策树的高度Args:treeReturns:树高"""if not isinstance(tree, dict):return 1child_trees = tree.values()[0].values()# 遍历子树, 获得子树的最大高度max_height = 0for child_tree in child_trees:child_tree_height = get_tree_height(child_tree)if child_tree_height > max_height:max_height = child_tree_heightreturn max_height + 1
#decisionTreePlot画图类
# 定义文本框 和 箭头格式 【 sawtooth 波浪方框, round4 矩形方框 , fc表示字体颜色的深浅 0.1~0.9 依次变浅,没错是变浅】
decisionNode=dict(boxstyle="sawtooth",fc="0.8")
leafNode=dict(boxstyle="round4",fc="0.8")
arrow_args=dict(arrowstyle="<-")def getNumLeafs(myTree):numLeafs=0firstStr=myTree.keys()[0]secondDict=myTree[firstStr]#根节点开始遍历for key in secondDict.keys():# 判断子节点是否为dict, 不是+1if type(secondDict[key]) is dict:numLeafs+=getNumLeafs(secondDict[key])else:numLeafs+=1return numLeafs
def getTreeDepth(myTree):maxDepth=0firstStr=myTree.keys()[0]secondDict=myTree[firstStr]#根节点开始遍历for key in secondDict.keys():# 判断子节点是不是dict, 求分枝的深度if type(secondDict[key]) is dict:thisDepth=1+getTreeDepth(secondDict[key])else:thisDepth=1#记录最大的分支深度if thisDepth>maxDepth:maxDepth=thisDepthreturn maxDepth
def plotNode(nodeTxt,centerPt,parentPt,nodeType):createPlot.ax1.annotate(nodeTxt,xy=parentPt,xycoords='axes fraction',xytext=centerPt,textcoords='axes fraction',va="center",ha="center",bbox=nodeType,arrowprops=arrow_args)
def plotMidText(cntrPt,parentPt,txtString):xMid=(parentPt[0]-cntrPt[0])/2.0+cntrPt[0]yMid=(parentPt[1]-cntrPt[1])/2.0+cntrPt[1]createPlot.ax1.text(xMid,yMid,txtString,va="center",ha="center",rotation=30)
'''
说明
函数.变量
如plotTree.xoff
表示plotTree的静态变量
def k():k.i=0
def k1():k.i=1
k1()
print(k.i)
输出为1
'''
def plotTree(myTree,parentPt,nodeTxt):#获取叶子节点的数量numLeafs=getNumLeafs(myTree)# 获取树的深度# depth = getTreeDepth(myTree)# 找出第1个中心点的位置,然后与 parentPt定点进行划线# x坐标为 (numLeafs-1.)/plotTree.totalW/2+1./plotTree.totalW,化简如下cntrPt=(plotTree.xoff+(1.0+float(numLeafs))/2.0/plotTree.totalW,plotTree.yoff)# print cntrPt# 并打印输入对应的文字plotMidText(cntrPt,parentPt,nodeTxt)firstStr=myTree.keys()[0]# 可视化Node分支点;第一次调用plotTree时,cntrPt与parentPt相同plotNode(firstStr,cntrPt,parentPt,decisionNode)#根节点的值secondDict=myTree[firstStr]# y值 = 最高点-层数的高度[第二个节点位置];1.0相当于树的高度plotTree.yoff = plotTree.yoff - 1.0 / plotTree.totalDfor key in secondDict.keys():# 判断该节点是否是Node节点if type(secondDict[key]) is dict:# 如果是就递归调用[recursion]plotTree(secondDict[key],cntrPt,str(key))else:# 如果不是,就在原来节点一半的地方找到节点的坐标plotTree.xoff=plotTree.xoff+1.0/plotTree.totalW# 可视化该节点位置plotNode(secondDict[key],(plotTree.xoff,plotTree.yoff),cntrPt,leafNode)# 并打印输入对应的文字plotMidText((plotTree.xoff,plotTree.yoff),cntrPt,str(key))plotTree.yoff=plotTree.yoff+1.0/plotTree.totalD
def createPlot(inTree):# 创建一个figure的模版fig=plt.figure(1,facecolor='green')fig.clf()axprops=dict(xticks=[],yticks=[])# 表示创建一个1行,1列的图,createPlot.ax1 为第 1 个子图,createPlot.ax1=plt.subplot(111,frameon=False,**axprops)plotTree.totalW=float(getNumLeafs(inTree))plotTree.totalD=float(getTreeDepth(inTree))print(plotTree.totalD)# 半个节点的长度;xOff表示当前plotTree未遍历到的最左的叶节点的左边一个叶节点的x坐标# 所有叶节点中,最左的叶节点的x坐标是0.5/plotTree.totalW(因为totalW个叶节点在x轴方向是平均分布在[0, 1]区间上的)# 因此,xOff的初始值应该是 0.5/plotTree.totalW-相邻两个叶节点的x轴方向距离plotTree.xoff=-0.5/plotTree.totalW# 根节点的y坐标为1.0,树的最低点y坐标为0plotTree.yoff=1.0# 第二个参数是根节点的坐标plotTree(inTree,(0.5,1.0),'')plt.show()
fishTest()
ef ContactLensesTest():"""Desc:预测隐形眼镜的测试代码Args:noneReturns:none"""# 加载隐形眼镜相关的 文本文件 数据fr=open('3.DecisionTree/lenses.txt')# 解析数据,获得 features 数据lenses=[inst.strip().split('\t') for inst in fr.readlines()]# 得到数据的对应的 LabelslensesLabels=['age','prescript','astigmatic','tearRate']# 使用上面的创建决策树的代码,构造预测隐形眼镜的决策树lensesTree=createTree(lenses,lensesLabels)print(lensesTree)#画图可视化展现createPlot(lensesTree)storeTree(lensesTree, "lensenTree")
ContactLensesTest()
相关文章:
决策树(Decision Tree)
决策树的定义: 分类决策树模型是一种描述对实例进行分类的树形结构。决策树由结点(node)和有向边(directed edge)组成。结点有两种类型: 内部结点(internal node)和叶结点(leaf node࿰…...

解决 PaddleClas 下载预训练模型报错 ModuleNotFoundError No module named ‘ppcls‘ 的问题
当我们在使用 PaddleClas 进行预训练模型下载时,可能会遇到一个报错,报错信息为 ModuleNotFoundError: No module named ppcls。这个错误通常是因为 Python 解释器无法找到名为 ppcls 的模块,而我们的代码中正尝试导入它。让我们一起来解决这…...
视觉化洞察:为什么我们需要数据可视化?
为什么我们需要数据可视化?这个问题在信息时代变得愈发重要。数据,如今已成为生活的一部分,我们每天都在产生大量的数据,从社交媒体到购物记录,从健康数据到工作表现,数据无处不在。然而,数据本…...

C语言函数概述——拜佛代码
函数是一种可重用的代码块,用于执行特定任务或完成特定功能函数作用:对具备相同逻辑的代码进行封装,提高代码的编写效率,实现对代码的重用函数作用演示代码: #include <stdio.h>// 定义函数 void func() {print…...

防火墙日志分析工具
防火墙提供对进入组织网络的网络流量的来源和类型的可见性,这使得防火墙日志成为重要的信息源,包括所有连接的源地址、目标地址、协议和端口号等详细信息,此信息可以提供对未知安全威胁的见解,是威胁管理中的重要工具。 防火墙日…...

Autofac中多个类继承同一个接口,如何注入?与抽象工厂模式相结合
多个类继承同一个接口,如何注入?与抽象工厂模式相结合 需求: 原来是抽象工厂模式,多个类继承同一个接口。 现在需要使用Autofac进行选择性注入。 Autofac默认常识: Autofac中多个类继承同一个接口,默认是最后一个接口注入的类。 解决方案:(约定大于配…...

Django系列之日志配置
如何配置 settings.py 文件中增加如下日志模块 """logger 配置""" LOGGING {version: 1,disable_existing_loggers: False, # 是否去掉目前项目中其他地方中以及使用的日志功能,但是将来我们可能会引入第三方的模块,里…...

四轴飞行器传感器(SimulinkMatlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
学习 使用pandas库 DataFrame 使用
1 、 数据排序 sort_values()函数 by:要排序的名称或名称列表, sorted_df df.sort_values(byAge,ascendingFalse) 由大到小排序; sorted_df df.sort_values(byAge) 由小到大排序; # 创建一个示例数据帧 data {Name: [Tom, Nick, John…...
C++字符串详解
C 大大增强了对字符串的支持,除了可以使用C风格的字符串,还可以使用内置的 string 类。string 类处理起字符串来会方便很多,完全可以代替C语言中的字符数组或字符串指针。 string 是 C 中常用的一个类,它非常重要,我们…...

vant2 van-calendar组件增加清除按钮和确定按钮
利用自定义插槽增加一个清除按钮 <van-calendar ref"fTime1" select"selectTimePicker" confirm"changeTimePicker" :default-date"null" :show-confirm"false" v-model"timePickerShow" type"range&quo…...
Spring redis使用报错Read timed out排查解决
文章目录 使用场景报错信息解决方式 使用场景 我们使用redis作为缓存服务,缓存一些业务数据,如路口点位信息、渠化信息、设备信息等有一些需要实时计算的数据,缓存在redis里,如实时信号周期相位、周期内过车数量等有需要不同服务…...
C语言每日一练-------Day(9)
本专栏为c语言练习专栏,适合刚刚学完c语言的初学者。本专栏每天会不定时更新,通过每天练习,进一步对c语言的重难点知识进行更深入的学习。 今日练习题关键字:字符个数统计 多数元素 投票法 💓博主csdn个人主页…...
SpringCloud(十)——ElasticSearch简单了解(三)数据聚合和自动补全
文章目录 1. 数据聚合1.1 聚合介绍1.2 Bucket 聚合1.3 Metrics 聚合1.4 使用 RestClient 进行聚合 2. 自动补全2.1 安装补全包2.2 自定义分词器2.3 自动补全查询2.4 拼音自动补全查询2.5 RestClient 实现自动补全2.5.1 建立索引2.5.2 修改数据定义2.5.3 补全查询2.5.4 解析结果…...
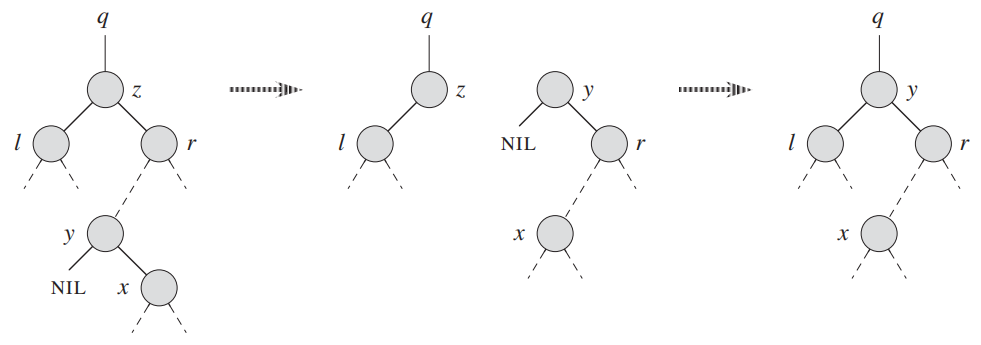
二叉查找树(binary search tree)(难度7)
C数据结构与算法实现(目录) 答案在此:二叉查找树(binary search tree)(答案) 写在前面 部分内容参《算法导论》 基本接口实现 1 删除 删除值为value的第一个节点 删除叶子节点1 删除叶子节…...
windows环境装MailHog
背景:win10系统,windows 宝塔,laravel 项目,邮件相关需要装一个MailHog 下载地址:https://sourceforge.net/projects/mailhog.mirror/ 直接下载,下载后双击运行就可以了,系统可能提示”不信任“…...

Ubuntu 22.04.2 LTS 安装python3.6后报错No module named ‘ufw‘
查明原因: vim /usr/sbin/ufw 初步判断是python版本的问题。 # 查看python3软链接 ll /usr/bin/python3 将python3的软链接从python3.6换成之前的3.10,根据自己电脑情况。 可以查看下 /usr/bin 下有什么 我这是python3.10 所以解决办法是 # 移除py…...
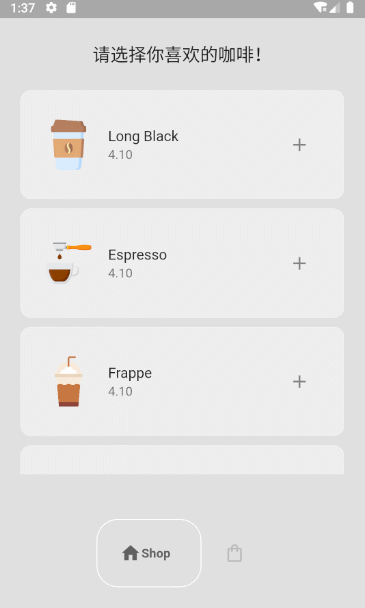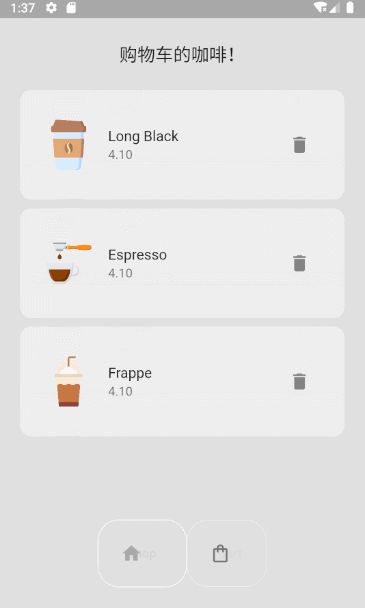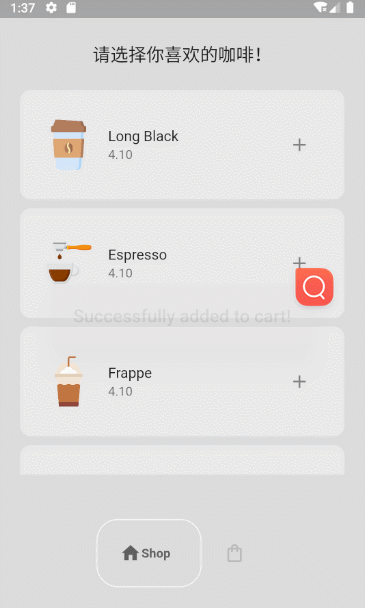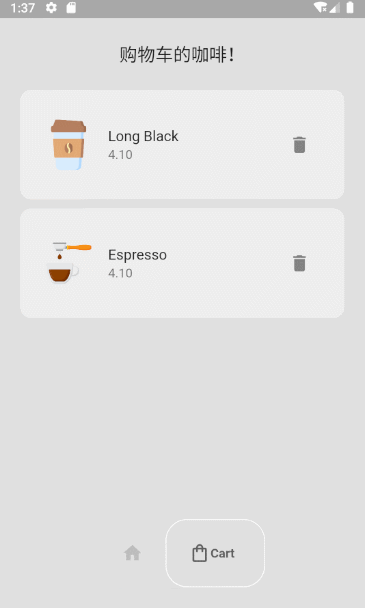
Flutter小功能实现-咖啡店
1 导航栏实现 效果图: 1.Package google_nav_bar: ^5.0.6 使用文档: google_nav_bar | Flutter Package 2.Code //MyBottomNavBar class MyBottomNavBar extends StatelessWidget {void Function(int)? onTabChange;MyBottomNavBar({super.key, …...

JavaSE 集合框架及背后的数据结构
目录 1 介绍2 学习的意义2.1 Java 集合框架的优点及作用2.2 笔试及面试题 3 接口 interfaces3.1 基本关系说明3.2 Collection 常用方法说明3.3 Collection 示例3.4 Map 常用方法说明3.5 Map 示例 4 实现 classes5 Java数据结构知识体系5.1 目标5.2 知识点 1 介绍 集合…...

-9501 MAL系统没有配置或者服务器不是企业版(dm8达梦数据库)
dm8达梦数据库 -9501 MAL系统没有配置或者服务器不是企业版) 环境介绍1 环境检查2 问题原因 环境介绍 搭建主备集群时,遇到报错-9501 MAL系统没有配置或者服务器不是企业版 1 环境检查 检查dmmal.ini配置文件权限正确 dmdba:dinstall,内容正…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...
