二叉查找树(binary search tree)(难度7)
C++数据结构与算法实现(目录)
答案在此:二叉查找树(binary search tree)(答案)
写在前面
部分内容参《算法导论》
基本接口实现
1 删除
删除值为value的第一个节点

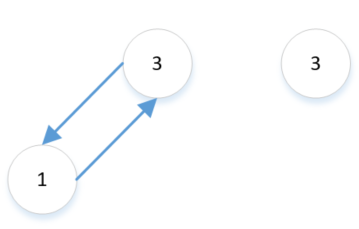
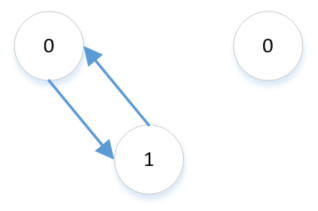
(3)删除叶子节点1
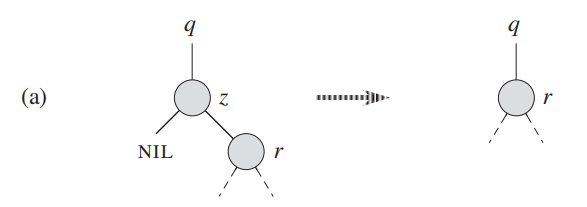

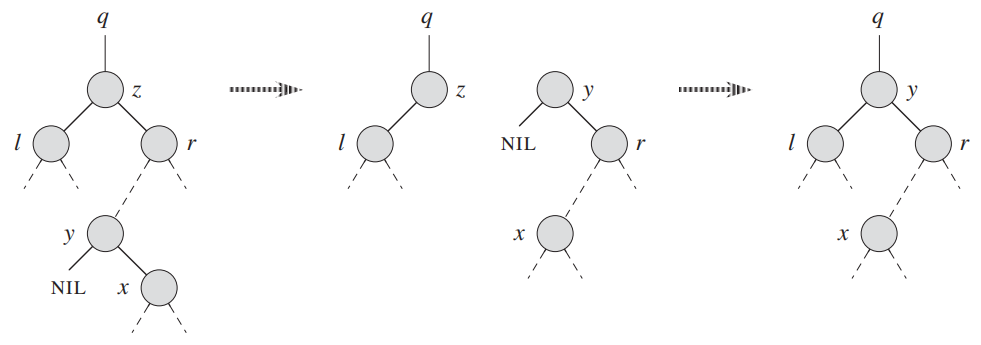
分成下面几个步骤进行:
1 找到z的后继,y是z的后继。这时候可以确定y是不可能有左孩子的。
2 删除y,让y的右孩子x取代自己的位置。删除只有一个孩子的节点上面已经讨论过。
3 让y的值覆盖z的值。
待实现代码
#pragma once
#include <algorithm>
#include <list>
#include <iostream>
#include <stack>
#include <queue>
#include <cstdlib>
#include <ctime>
#include <string>
#include <cassert>
#include <map>
#include <sstream>
using namespace std;//------下面的代码是用来测试你的代码有没有问题的辅助代码,你无需关注------
#include <algorithm>
#include <cstdlib>
#include <iostream>
#include <vector>
#include <utility>
using namespace std;
struct Record { Record(void* ptr1, size_t count1, const char* location1, int line1, bool is) :ptr(ptr1), count(count1), line(line1), is_array(is) { int i = 0; while ((location[i] = location1[i]) && i < 100) { ++i; } }void* ptr; size_t count; char location[100] = { 0 }; int line; bool is_array = false; bool not_use_right_delete = false; }; bool operator==(const Record& lhs, const Record& rhs) { return lhs.ptr == rhs.ptr; }std::vector<Record> myAllocStatistic; void* newFunctionImpl(std::size_t sz, char const* file, int line, bool is) { void* ptr = std::malloc(sz); myAllocStatistic.push_back({ ptr,sz, file, line , is }); return ptr; }void* operator new(std::size_t sz, char const* file, int line) { return newFunctionImpl(sz, file, line, false); }void* operator new [](std::size_t sz, char const* file, int line)
{return newFunctionImpl(sz, file, line, true);
}void operator delete(void* ptr) noexcept { Record item{ ptr, 0, "", 0, false }; auto itr = std::find(myAllocStatistic.begin(), myAllocStatistic.end(), item); if (itr != myAllocStatistic.end()) { auto ind = std::distance(myAllocStatistic.begin(), itr); myAllocStatistic[ind].ptr = nullptr; if (itr->is_array) { myAllocStatistic[ind].not_use_right_delete = true; } else { myAllocStatistic[ind].count = 0; }std::free(ptr); } }void operator delete[](void* ptr) noexcept { Record item{ ptr, 0, "", 0, true }; auto itr = std::find(myAllocStatistic.begin(), myAllocStatistic.end(), item); if (itr != myAllocStatistic.end()) { auto ind = std::distance(myAllocStatistic.begin(), itr); myAllocStatistic[ind].ptr = nullptr; if (!itr->is_array) { myAllocStatistic[ind].not_use_right_delete = true; } else { myAllocStatistic[ind].count = 0; }std::free(ptr); } }
#define new new(__FILE__, __LINE__)
struct MyStruct { void ReportMemoryLeak() { std::cout << "Memory leak report: " << std::endl; bool leak = false; for (auto& i : myAllocStatistic) { if (i.count != 0) { leak = true; std::cout << "leak count " << i.count << " Byte" << ", file " << i.location << ", line " << i.line; if (i.not_use_right_delete) { cout << ", not use right delete. "; } cout << std::endl; } }if (!leak) { cout << "No memory leak." << endl; } }~MyStruct() { ReportMemoryLeak(); } }; static MyStruct my; void check_do(bool b, int line = __LINE__) { if (b) { cout << "line:" << line << " Pass" << endl; } else { cout << "line:" << line << " Ohh! not passed!!!!!!!!!!!!!!!!!!!!!!!!!!!" << " " << endl; exit(0); } }
#define check(msg) check_do(msg, __LINE__);
//------上面的代码是用来测试你的代码有没有问题的辅助代码,你无需关注------template<typename T>
class binary_search_tree
{
private:struct tree_node//OK{tree_node() :data(T()){}tree_node(const T& t) :data(t){}bool exist_parent(void) const { return parent != nullptr; }T data;tree_node* parent = nullptr;tree_node* left = nullptr;tree_node* right = nullptr;};
public:binary_search_tree(void) :m_root(nullptr) {}//默认构造函数:什么也不需要做,因为成员定义的时候就已经初始化了binary_search_tree(const T*, const int);//从数组构造一颗二叉树binary_search_tree(const binary_search_tree&);//拷贝构造函数binary_search_tree& operator = (const binary_search_tree&);~binary_search_tree(void) { clear(); }//析构函数
public:int size(void) const;//元素数量bool empty(void) const { return size() == 0; }//二叉树是否为空bool insert(const T& data);//插入一个元素T minmum(void) const;//最小值T maxmum(void) const;//最大值bool exists(const T& data) const;//判断元素是否存在void clear(void);//非递归清空二叉树void erase(const T& data);template<typename T>friend ostream& operator<<(ostream& out, const binary_search_tree<T>& tree);//输出二叉树void print_pre_order_nonrecursive(void) const;//非递归:先序遍历输出二叉树void print_in_order_nonrecursive(void) const;//非递归:中序遍历输出二叉树void print_post_order_nonrecursive(void) const;//非递归:后续遍历输出二叉树void print_in_order_recursive(std::ostream& os) const;//递归中序遍历输出二叉树void print_element_order(void) const;//非递归按元素顺序输出二叉树std::string to_string_in_order(void) const;int max_length_between_node(void) const;//最大节点距离int hight(void) const;//树高度bool operator==(const binary_search_tree& other) const;//两个树相等:结构相同,对应元素相同bool operator!=(const binary_search_tree& other) const { return !equal(other); }//两个树不相等bool equal(const binary_search_tree& other) const;//两个树相等:结构相同,对应元素相同
private:void print_binary_tree(ostream&, const tree_node* bt, int depth) const;//二叉树形式打印二叉树tree_node* find(const T& data);//查找tree_node* maxmum(tree_node*) const;//最大节点tree_node* minmum(tree_node*) const;//最小节点tree_node* successor(tree_node* t) const;//后继节点//节点的深度与高度:对于树中相同深度的每个结点来说,它们的高度不一定相同,这取决于每个结点下面的叶结点的深度int hight(const tree_node* _t) const;bool equal(const tree_node* lhs, const tree_node* rhs) const;//两个树相等:结构相同,对应元素相同bool is_node_leaf(const tree_node* node) const;bool is_left_child(const tree_node* parent, const tree_node* node);bool is_leaf_node_equal(const tree_node* lhs, const tree_node* rhs) const;void copy(const binary_search_tree& other);void copy_node_from(tree_node*& dest, tree_node* dest_parent, const tree_node* from);void print_in_order_recursive(std::ostream& os, const tree_node* node) const;//递归中序遍历输出二叉树void erase_node(tree_node*& pnode);//参数是引用类型,主要是为了:erase_node(m_root) 时,更新m_root;void erase_and_reconnect(tree_node*& pnode, tree_node* pnode_child);void update_parent(tree_node* pnode);//删除叶子结点后,让父节点指向空指针
private:tree_node* left(tree_node* p){assert(p != nullptr);return p->left;}
private:tree_node* m_root = nullptr;//OKint m_size = 0;
};
template<typename T>
std::string binary_search_tree<T>::to_string_in_order(void) const
{std::stringstream oss;this->print_in_order_recursive(oss);auto str = oss.str();return str;
}
template<typename T>
binary_search_tree<T>::binary_search_tree(const T* arr, const int length) : binary_search_tree()
{//(4) your code //可以使用成员函数insert(const T& data) 来实现这个函数
}
template<typename T>
inline binary_search_tree<T>::binary_search_tree(const binary_search_tree & from) :m_root(nullptr)
{//(5) your code //可以使用成员函数copy来实现
}
template<typename T>
binary_search_tree<T>& binary_search_tree<T>::operator=(const binary_search_tree & from)
{//(5) your code //可以使用成员函数copy来实现。//从这里可以看出copy函数应该先用clear成员函数清空自己原有的全部节点return *this;
}
template<typename T>
void binary_search_tree<T>::copy(const binary_search_tree& other)
{if (this == &other)//如果拷贝自己,则什么也不做{return;//直接返回}clear();//先清空自己的内容m_size = other.m_size;//成员变量赋值if (other.m_root)//从根节点开始拷贝;递归的拷贝二叉树的每一个节点,照葫芦画瓢{copy_node_from(m_root/*需要被创建的节点*/, nullptr/*需要被创建的节点的父节点:用户指向孩子*/, other.m_root/*提供节点存储的数据*/);}
}
template<typename T>
bool binary_search_tree<T>::insert(const T& data)
{if (m_root != nullptr){tree_node *fast, *slow, *ptemp;fast = slow = ptemp = m_root;while (fast != 0){slow = fast;if (data < slow->data){fast = slow->left;}else if (data > slow->data){fast = slow->right;}else//esle equal do nothing 元素不允许重复//,元素如果已经存在,什么也不做{fast = 0;return false;//直接退出,不再插入相同的元素的}}if (data < slow->data){slow->left = new tree_node(data);slow->left->parent = slow;}else if (data > slow->data){slow->right = new tree_node(data);slow->right->parent = slow;}else{return false;}//esle equal do nothing}else{m_root = new tree_node(data);}++m_size;return true;
}
template<typename T>
int binary_search_tree<T>::hight(void) const
{return hight(m_root);
}
template<typename T>
int binary_search_tree<T>::hight(const tree_node* _t) const
{//树的高度,也是树的层树,最大层的层数就是树的高度//(7) your code 如果没有元素,返回0// 如果只有一个根节点,没有孩子节点高度为1// 如果有孩子节点,树的高度就 = 1 + 孩子节点的高度(左右子树高度较大的那一个)return -1;
}
template<typename T>
bool binary_search_tree<T>::operator==(const binary_search_tree & other) const
{return this->equal(other);//两个二叉树相等,当且仅当两颗树长的一模一样
}
template<typename T>
bool binary_search_tree<T>::equal(const binary_search_tree & other) const
{return equal(m_root, other.m_root);
}
template<typename T>
bool binary_search_tree<T>::equal(const tree_node* lhs, const tree_node* rhs) const
{// 先判断两个树是否为空//再判断两个树是否都是叶子节点 可以使用 is_leaf_node_equal 成员函数//再判断两个树的两个左右子树是否同时相等 可以递归调用当前equal函数//(8) your codereturn false;
}
template<typename T>
inline bool binary_search_tree<T>::is_leaf_node_equal(const tree_node* lhs, const tree_node* rhs) const
{if (is_node_leaf(lhs) && is_node_leaf(rhs)){return lhs->data == rhs->data;}return false;
}
template<typename T>
inline bool binary_search_tree<T>::is_node_leaf(const tree_node * node) const
{return node != nullptr && node->left == nullptr && node->right == nullptr;
}template<typename T>
///*需要被创建的节点*/, nullptr/*需要被创建的节点*/, other.m_root/*提供节点存储的数据*/
void binary_search_tree<T>::copy_node_from(tree_node *& dest, tree_node* dest_parent, const tree_node * from)
{//(9) your code 深度拷贝from节点,并切递归拷贝,从而完成整棵树的拷贝//注意dest节点传递的是引用,这意味着你可以非常方便的对这个地址变量赋值,赋值就会修改传进来的外部变量//改函数使用递归调用自己的方式,完成整棵树的拷贝。注意对左子树和又子树可能需要分别调用一次递归函数才能完成。}template<typename T>
int binary_search_tree<T>::max_length_between_node(void) const
{int max_length = 0;const tree_node* ptree = m_root;list<tree_node*> listNode;listNode.push_back(m_root);while (!listNode.empty()){auto pnode = listNode.front();listNode.pop_front();if (pnode->left != nullptr){listNode.push_back(pnode->left);}if (pnode->right != nullptr){listNode.push_back(pnode->right);}int tempBetween = hight(pnode->left) + hight(pnode->right);max_length = std::max<int>(tempBetween, max_length);}return max_length;
}
template<typename T>
void binary_search_tree<T>::clear(void)
{//使用一个辅助队列(或者栈),层次遍历删除所有节点。//遍历到一个节点A就把孩子BC放到队列,并把这个节点A从队列里取出释放//(10) your code}
template<typename T>
void binary_search_tree<T>::print_binary_tree(ostream& out, const tree_node* bt, int depth) const
{//用右左孩子的方式输出一颗树,先输出右孩子后输出左孩子if (bt){print_binary_tree(out, bt->right, depth + 1);if (depth == 0){out << bt->data << endl;}else if (depth == 1){out << " --" << bt->data << endl;}else{int n = depth;while (--n){cout << " ";}out << " --" << bt->data << endl;}print_binary_tree(out, bt->left, depth + 1);}
}
template<typename T>
void binary_search_tree<T>::print_in_order_nonrecursive(void) const
{cout << "print_in_order_nonrecursive : ";stack<tree_node*> tempstack;tree_node* t = m_root;if (t != NULL){do{tempstack.push(t);t = t->left;} while (t != NULL);}while (!tempstack.empty()){tree_node* p = tempstack.top();cout << p->data << " ";tempstack.pop();if (p->right != NULL){p = p->right;do{tempstack.push(p);p = p->left;} while (p != NULL);}}cout << endl;
}
template<typename T>
inline void binary_search_tree<T>::print_in_order_recursive(std::ostream & os) const
{print_in_order_recursive(os, m_root);
}
template<typename T>
void binary_search_tree<T>::print_in_order_recursive(std::ostream & os, const tree_node * node) const
{if (node == nullptr){return;}print_in_order_recursive(os, node->left);os << node->data << " ";print_in_order_recursive(os, node->right);
}
template<typename T>
ostream& operator<<(ostream& out, const binary_search_tree<T>& tree)
{tree.print_binary_tree(out, tree.m_root, 0);return out;
}
template<typename T>
void binary_search_tree<T>::print_post_order_nonrecursive(void) const
{//后续序序遍历输出一颗树的全部结点值2,3,1//广度优先遍历cout << "print_post_order_nonrecursive : ";typedef pair<tree_node*, bool> multinode;stack<multinode> tempstack;if (m_root){tempstack.push(make_pair(m_root, false));}while (!tempstack.empty()){multinode m = tempstack.top(); tempstack.pop();if (m.first->left == NULL && m.first->right == NULL){//叶子节点直接输出cout << m.first->data << " ";}else if (m.second == true){//所有孩子都遍历完了才会到这一步cout << m.first->data << " ";}else{//非终结点,并且孩子还没遍历完。m.second = true; tempstack.push(m);if (m.first->right != NULL){tempstack.push(make_pair(m.first->right, false));}if (m.first->left != NULL){tempstack.push(make_pair(m.first->left, false));}}}cout << endl;
}
template<typename T>
void binary_search_tree<T>::print_pre_order_nonrecursive(void) const
{//先序遍历输出一颗树的全部结点值1,2,3,先根遍历cout << "print_pre_order_nonrecursive : ";stack<tree_node*> node_stack;if (m_root){node_stack.push(m_root);tree_node* t;while (!node_stack.empty()){t = node_stack.top();node_stack.pop();cout << t->data << " ";if (t->right != 0){node_stack.push(t->right);}if (t->left != 0){node_stack.push(t->left);}}cout << endl;}
}
template<typename T>
bool binary_search_tree<T>::exists(const T& data) const
{bool result = false;if (m_root){tree_node* pfind = m_root;while (pfind){if (pfind->data == data){result = true;break;}else if (data < pfind->data){pfind = pfind->left;}elsepfind = pfind->right;}}return result;
}
template<typename T>
typename binary_search_tree<T>::tree_node* binary_search_tree<T>::find(const T& data)
{//(11) your code 利用find,非递归实现:查找某个值是否存在于树中return nullptr;
}template<typename T>
int binary_search_tree<T>::size(void) const
{return m_size;
}
template<typename T>
T binary_search_tree<T>::minmum(void) const
{//(12) your code 返回最小值 ,请使用成员函数 minmum(tree_node* p) const 来实现return T();
}
template<typename T>
typename binary_search_tree<T>::tree_node* binary_search_tree<T>::minmum(tree_node* p) const
{//(13) your code 返回最小值:非递归实现return nullptr;
}
template<typename T>
T binary_search_tree<T>::maxmum(void) const
{//(14) your code 返回最大值 ,请使用成员函数 maxmum(tree_node* p) const 来实现return T();
}
template<typename T>
typename binary_search_tree<T>::tree_node* binary_search_tree<T>::maxmum(tree_node* t) const
{//(14) your code 返回最大值:非递归实现return nullptr;
}
template<typename T>
typename binary_search_tree<T>::tree_node* binary_search_tree<T>::successor(tree_node* t) const
{//(15) your code 找到一个节点的后继结点,这个函数是顺序迭代遍历二叉树的关键函数。//具体思路为,如果这个节点有右子树,那么右子树的minmum节点就是后继结点。//如果,这个节点没有右子树,比该节点大的值,一定是往右上方去的第一个节点。//参考《算法导论》return nullptr;
}
template<typename T>
void binary_search_tree<T>::print_element_order(void) const
{cout << "print_element_order by order: ";if (!empty()){//(16) your code 使用后继节点成员函数作为顺序迭代的依据,实现顺序遍历一颗二次函数。//循环获取后继,只要有后继,就输出这个后继。cout << endl;}
}template<typename T>
void binary_search_tree<T>::erase(const T& data)
{tree_node* itr = find(data);assert(itr != nullptr);--m_size;if (itr == m_root){/*删除根节点,可能需要释放根节点本身,这个时候m_root的指向需要更新。* 所以erase_node的参数是引用类型,希望可以在erase_node内部对m_root重新* 赋值来打到更新根节点指向的目的。*/erase_node(m_root);return;}else{erase_node(itr);}
}
template<typename T>
void binary_search_tree<T>::erase_node(tree_node*& pnode)
{//pnode如果没有parent,那么它就是root,这个时候,删除pnode// ,无需考虑pnode的parent需要更新的问题。//只需要处理其孩子替代自己的问题if (pnode->left == nullptr && pnode->right == nullptr){//叶子结点被删除了的话,被删除节点的父亲应该指向空指针。update_parent(pnode);//内部会先判断pnode有没有parentdelete pnode;//这里会更新传进来的引用参数,比如,如果传进来的是m_root的话。pnode = nullptr;//如果pnode是m_root的话,这句话就会变得必不可少(更新m_root)}//如果被删除的节点p只有左孩子:让p的左孩子p_left_child取代自己作为p的parent节点的做孩子else if (pnode->left != nullptr && pnode->right == nullptr){//让pnode的父亲节点和pnode的孩子建立连接erase_and_reconnect(pnode, pnode->left);}//如果只有右孩子:让右孩子取代自己else if (pnode->left == nullptr && pnode->right != nullptr){//让pnode的父亲节点和pnode的孩子建立连接erase_and_reconnect(pnode, pnode->right);}else{//https://zhuanlan.zhihu.com/p/640863892//分成下面几个步骤进行://1 找到z的后继,y是z的后继。这时候可以确定y是不可能有左孩子的。//2 删除y,让y的右孩子x取代自己的位置。删除只有一个孩子的节点上面已经讨论过。//3 让y的值覆盖z的值。tree_node* psuccessor = successor(pnode);pnode->data = psuccessor->data;//3 让y的值覆盖z的值。//2 删除y, y只有一个孩子,只有一个孩子的节点删除此函数的开始部分已经实现了。只需要调用此函数即可。//(17) your code}
}
template<typename T>
void binary_search_tree<T>::update_parent(tree_node* pnode)
{//删除叶子结点后,让父节点指向空指针if (pnode->parent){auto parent = pnode->parent;is_left_child(parent, pnode) ? (parent->left = nullptr) : (parent->right = nullptr);}
}
template<typename T>
void binary_search_tree<T>::erase_and_reconnect(tree_node*& delete_pnode, tree_node* pnode_child)
{//让左孩子取代自己,同时考虑parent不存在的情况下取代自己。if (delete_pnode->exist_parent()){//拿到父节点auto parent = delete_pnode->parent;auto is_left = is_left_child(parent, delete_pnode);//先备份地址,将来用于释放内存auto pbackup = delete_pnode;//指向新节点:自己的左孩子替代自己// reconnect1 ->delete_pnode = pnode_child;// <- reconnect2 pnode_child->parent = parent;//指向新的父亲//删除自己原来的内存delete pbackup;//父节点和自己的左孩子建立连接is_left ? parent->left = delete_pnode : parent->right = delete_pnode;}else //删除根节点, 删除根节点可不是删除整个树哦{//先备份地址,将来用于释放内存auto pbackup = delete_pnode;//指向新节点:自己的左孩子替代自己delete_pnode = pnode_child;//删除自己原来的内存delete pbackup;}
}
template<typename T>
bool binary_search_tree<T>::is_left_child(const tree_node* parent, const tree_node* pnode)
{assert(parent != nullptr);assert(pnode != nullptr);return (parent->left == pnode);
}void test_tree(const binary_search_tree<int>& _tree)
{cout << "test_tree:\n";cout << _tree;cout << "tree size : " << _tree.size() << endl;cout << "tree max length between node " << _tree.max_length_between_node() << endl;_tree.print_in_order_nonrecursive();_tree.print_element_order();_tree.print_post_order_nonrecursive();_tree.print_pre_order_nonrecursive();cout << "min element : " << _tree.minmum() << endl;cout << "max element : " << _tree.maxmum() << "\n" << endl;
}
void test1()
{binary_search_tree<int> tree;check(tree.size() == 0);check(tree.empty());check(tree.hight() == 0);
}
void test2()
{int arr[1] = { 1 };binary_search_tree<int> tree(arr, 1);check(tree.size() == 1);check(tree.to_string_in_order() == "1 ");check(!tree.empty());
}
void test3()
{int arr[2] = { 1, 2 };binary_search_tree<int> tree(arr, 2);check(tree.size() == 2);check(tree.to_string_in_order() == "1 2 ");check(!tree.empty());
}
void test4()
{int arr[2] = { 2, 1 };binary_search_tree<int> tree(arr, 2);check(tree.size() == 2);check(tree.to_string_in_order() == "1 2 ");check(!tree.empty());
}
void test5()
{constexpr int length = 3;int arr[length] = { 1, 2, 3 };binary_search_tree<int> tree(arr, length);check(tree.size() == length);check(tree.to_string_in_order() == "1 2 3 ");check(!tree.empty());
}
void test6()
{constexpr int length = 3;int arr[length] = { 2, 1, 3 };binary_search_tree<int> tree(arr, length);check(tree.size() == length);check(tree.to_string_in_order() == "1 2 3 ");check(!tree.empty());
}
void test7()
{constexpr int length = 3;int arr[length] = { 3, 2, 1, };binary_search_tree<int> tree(arr, length);check(tree.size() == length);check(tree.to_string_in_order() == "1 2 3 ");check(!tree.empty());
}
void test8()
{constexpr int length = 3;int arr[length] = { 3, 1, 2, };binary_search_tree<int> tree(arr, length);check(tree.size() == length);check(tree.to_string_in_order() == "1 2 3 ");check(!tree.empty());
}
void test9()
{constexpr int length = 10;int arr[length] = { 1,3,5,7,9,2,4,6,8,10 };binary_search_tree<int> tree(arr, length);check(tree.size() == length);check(tree.to_string_in_order() =="1 2 3 4 5 6 7 8 9 10 ");check(!tree.empty());
}
void test10()
{constexpr int length = 10;int arr[length] = { 2,4,6,8,10,1,3,5,7,9 };binary_search_tree<int> tree(arr, length);check(tree.size() == length);check(tree.to_string_in_order() =="1 2 3 4 5 6 7 8 9 10 ");check(!tree.empty());
}
void test11()
{constexpr int length = 10;int arr[length] = { 10,9,8,7,6,5,4,3,2,1 };binary_search_tree<int> tree(arr, length);check(tree.size() == length);check(tree.to_string_in_order() =="1 2 3 4 5 6 7 8 9 10 ");check(!tree.empty());check(tree.hight() == 10);
}
void test12()
{constexpr int length = 10;int arr[length] = { 5,4,3,2,1,10,9,8,7,6 };binary_search_tree<int> tree(arr, length);check(tree.size() == length);check(tree.to_string_in_order() =="1 2 3 4 5 6 7 8 9 10 ");check(!tree.empty());check(tree.hight() == 6);
}
void test13()
{constexpr int length = 1;int arr[length] = { 1 };binary_search_tree<int> tree(arr, length);check(tree.minmum() == 1);check(tree.maxmum() == 1);check(tree.hight() == 1);
}
void test14()
{constexpr int length = 2;int arr[length] = { 1, 2 };binary_search_tree<int> tree(arr, length);check(tree.minmum() == 1);check(tree.maxmum() == 2);check(tree.hight() == 2);
}
void test15()
{constexpr int length = 10;int arr[length] = { 5,4,3,2,1,10,9,8,7,6 };binary_search_tree<int> tree(arr, length);check(tree.minmum() == 1);check(tree.maxmum() == 10);
}
void test16()
{constexpr int length = 1;int arr[length] = { 1 };binary_search_tree<int> tree(arr, length);check(tree.exists(1));tree.erase(1);check(!tree.exists(1));check(tree.size() == 0);
}
void test17()
{int arr[] = { 3,2,1 };binary_search_tree<int> tree(arr, sizeof(arr) / sizeof(int));check(tree.exists(1));cout << tree << endl;tree.erase(2);cout << tree << endl;check(!tree.exists(2));check(tree.size() == 2);check(!tree.empty());check(tree.to_string_in_order() == "1 3 ");
}
void test18()
{constexpr int length = 2;int arr[length] = { 1, 2 };binary_search_tree<int> tree(arr, length);check(tree.exists(1));check(tree.exists(2));tree.erase(1);check(!tree.exists(1));check(tree.exists(2));tree.clear();check(tree.empty());check(tree.size() == 0);check(!tree.exists(2));
}
void test19()
{constexpr int length = 10;int arr[length] = { 5,3,4,1,2,10,8,9,7,6 };binary_search_tree<int> tree(arr, length);cout << tree << endl << "-------------------" << endl;tree.erase(1);cout << tree << endl << "-------------------" << endl;check(tree.to_string_in_order() == "2 3 4 5 6 7 8 9 10 ");tree.erase(2);cout << tree << endl << "-------------------" << endl;check(tree.to_string_in_order() == "3 4 5 6 7 8 9 10 ");tree.erase(3);check(tree.to_string_in_order() == "4 5 6 7 8 9 10 ");cout << tree << endl << "-------------------" << endl;tree.erase(4);cout << tree << endl << "-------------------" << endl;check(tree.to_string_in_order() == "5 6 7 8 9 10 ");tree.erase(5);cout << tree << endl << "-------------------" << endl;check(tree.to_string_in_order() == "6 7 8 9 10 ");tree.erase(6);cout << tree << endl << "-------------------" << endl;check(tree.to_string_in_order() == "7 8 9 10 ");tree.erase(7);cout << tree << endl << "-------------------" << endl;check(tree.to_string_in_order() == "8 9 10 ");tree.erase(8);cout << tree << endl << "-------------------" << endl;check(tree.to_string_in_order() == "9 10 ");tree.erase(9);cout << tree << endl << "-------------------" << endl;check(tree.to_string_in_order() == "10 ");tree.erase(10);cout << tree << endl << "-------------------" << endl;check(tree.to_string_in_order() == "");
}
void test20()
{constexpr int length = 10;int arr[length] = { 5,3,4,1,2,10,8,9,7,6 };binary_search_tree<int> tree(arr, length);cout << tree << endl << "-------------------" << endl;tree.erase(10);cout << tree << endl << "-------------------" << endl;check(tree.to_string_in_order() == "1 2 3 4 5 6 7 8 9 ");tree.erase(8);cout << tree << endl << "-------------------" << endl;check(tree.to_string_in_order() == "1 2 3 4 5 6 7 9 ");
}
void test21()
{constexpr int length = 10;int arr[length] = { 5,3,4,1,2,10,8,9,7,6 };binary_search_tree<int> tree(arr, length);cout << tree << endl << "-------------------" << endl;tree.erase(5);cout << tree << endl << "-------------------" << endl;check(tree.to_string_in_order() == "1 2 3 4 6 7 8 9 10 ");
}
void test22()
{constexpr int length = 10;int arr[length] = { 2,4,6,8,10,1,3,5,7,9 };binary_search_tree<int> tree(arr, length);check(tree.hight() == 6);tree.erase(1);check(!tree.exists(1));tree.erase(2);check(!tree.exists(2));tree.erase(3);check(!tree.exists(3));tree.erase(4);check(!tree.exists(4));tree.erase(5);check(!tree.exists(5));check(tree.to_string_in_order() == "6 7 8 9 10 ");tree.erase(6);check(!tree.exists(6));tree.erase(7);check(!tree.exists(7));tree.erase(8);check(!tree.exists(8));tree.erase(9);check(!tree.exists(9));tree.erase(10);check(!tree.exists(10));check(tree.empty());
}
void test23()
{//test equalint a[3] = { 15, 12, 14 };binary_search_tree<int> tree(a, 3);check(tree.hight() == 3);cout << "tree:\n" << tree << endl;auto tree2 = tree;cout << "tree2:\n" << tree2 << endl;check(tree2.equal(tree));
}
void test24(binary_search_tree<int>& tree)
{cout << "tree:\n" << tree << endl;auto tree2 = tree;cout << "tree2:\n" << tree2 << endl;check(tree2.equal(tree));check(tree2 == tree);tree.clear();cout << tree << endl;check(tree2.equal(tree) == false);check(tree2 != tree);
}
void test25()
{int a[3] = { 15, 12, 14 };binary_search_tree<int> tree(a, 3);tree.print_in_order_recursive(cout);
}
int main()
{test1();//emptytest2();//test create insert empty sizetest3();test4();test5();test6();test7();test8();test9();test10();test11();test12();test13();test14();//minmum maxmumtest15();test16();//exists clear erase size emptytest17();//erasetest18();//erasetest19();//erasetest20();//erasetest21();//erasetest22();//erasetest23();int maxLength = 0;int a[100] = { 15, 12, 14, 13, 16, 34, 23, 24, 22, 21, 20, 19, 18, 17, 35, 36, 37, 38, 39, 40, 41, 0 };binary_search_tree<int> tree(a, 22);check(tree.size() == 22);check(tree.empty() == false);check(tree.maxmum() == 41);check(tree.minmum() == 0);test_tree(tree);binary_search_tree<int> tree1(a, 3);test_tree(tree1);test24(tree);//test copytest25();//printreturn 0;
}
正确输出
line:725 Pass
line:726 Pass
line:727 Pass
line:733 Pass
line:734 Pass
line:735 Pass
line:741 Pass
line:742 Pass
line:743 Pass
line:749 Pass
line:750 Pass
line:751 Pass
line:758 Pass
line:759 Pass
line:760 Pass
line:767 Pass
line:768 Pass
line:769 Pass
line:776 Pass
line:777 Pass
line:778 Pass
line:785 Pass
line:786 Pass
line:787 Pass
line:794 Pass
line:796 Pass
line:797 Pass
line:804 Pass
line:806 Pass
line:807 Pass
line:814 Pass
line:816 Pass
line:817 Pass
line:818 Pass
line:825 Pass
line:827 Pass
line:828 Pass
line:829 Pass
line:836 Pass
line:837 Pass
line:838 Pass
line:845 Pass
line:846 Pass
line:847 Pass
line:854 Pass
line:855 Pass
line:862 Pass
line:864 Pass
line:865 Pass
line:871 Pass
3--2--13--1line:875 Pass
line:876 Pass
line:877 Pass
line:878 Pass
line:885 Pass
line:886 Pass
line:888 Pass
line:889 Pass
line:891 Pass
line:892 Pass
line:893 Pass--10--9--8--7--6
5--4--3--2--1---------------------10--9--8--7--6
5--4--3--2-------------------
line:903 Pass--10--9--8--7--6
5--4--3-------------------
line:906 Pass
line:908 Pass--10--9--8--7--6
5--4---------------------10--9--8--7--6
5-------------------
line:912 Pass
10--9--8--7--6-------------------
line:915 Pass
10--9--8--7-------------------
line:918 Pass
10--9--8-------------------
line:921 Pass
10--9-------------------
line:924 Pass
10-------------------
line:927 Pass-------------------
line:930 Pass--10--9--8--7--6
5--4--3--2--1---------------------9--8--7--6
5--4--3--2--1-------------------
line:940 Pass--9--7--6
5--4--3--2--1-------------------
line:943 Pass--10--9--8--7--6
5--4--3--2--1---------------------10--9--8--7
6--4--3--2--1-------------------
line:953 Pass
line:960 Pass
line:962 Pass
line:964 Pass
line:966 Pass
line:968 Pass
line:970 Pass
line:971 Pass
line:973 Pass
line:975 Pass
line:977 Pass
line:979 Pass
line:981 Pass
line:982 Pass
line:989 Pass
tree:
15--14--12tree2:
15--14--12line:993 Pass
line:1047 Pass
line:1048 Pass
line:1049 Pass
line:1050 Pass
test_tree:--41--40--39--38--37--36--35--34--24--23--22--21--20--19--18--17--16
15--14--13--12--0
tree size : 22
tree max length between node 14
print_in_order_nonrecursive : 0 12 13 14 15 16 17 18 19 20 21 22 23 24 34 35 36 37 38 39 40 41
print_element_order by order: 0 12 13 14 15 16 17 18 19 20 21 22 23 24 34 35 36 37 38 39 40 41
print_post_order_nonrecursive : 0 13 14 12 17 18 19 20 21 22 24 23 41 40 39 38 37 36 35 34 16 15
print_pre_order_nonrecursive : 15 12 0 14 13 16 34 23 22 21 20 19 18 17 24 35 36 37 38 39 40 41
min element : 0
max element : 41test_tree:
15--14--12
tree size : 3
tree max length between node 2
print_in_order_nonrecursive : 12 14 15
print_element_order by order: 12 14 15
print_post_order_nonrecursive : 14 12 15
print_pre_order_nonrecursive : 15 12 14
min element : 12
max element : 15tree:--41--40--39--38--37--36--35--34--24--23--22--21--20--19--18--17--16
15--14--13--12--0tree2:--41--40--39--38--37--36--35--34--24--23--22--21--20--19--18--17--16
15--14--13--12--0line:1000 Pass
line:1001 Passline:1004 Pass
line:1005 Pass
12 14 15 Memory leak report:
No memory leak.相关文章:

二叉查找树(binary search tree)(难度7)
C数据结构与算法实现(目录) 答案在此:二叉查找树(binary search tree)(答案) 写在前面 部分内容参《算法导论》 基本接口实现 1 删除 删除值为value的第一个节点 删除叶子节点1 删除叶子节…...
windows环境装MailHog
背景:win10系统,windows 宝塔,laravel 项目,邮件相关需要装一个MailHog 下载地址:https://sourceforge.net/projects/mailhog.mirror/ 直接下载,下载后双击运行就可以了,系统可能提示”不信任“…...

Ubuntu 22.04.2 LTS 安装python3.6后报错No module named ‘ufw‘
查明原因: vim /usr/sbin/ufw 初步判断是python版本的问题。 # 查看python3软链接 ll /usr/bin/python3 将python3的软链接从python3.6换成之前的3.10,根据自己电脑情况。 可以查看下 /usr/bin 下有什么 我这是python3.10 所以解决办法是 # 移除py…...
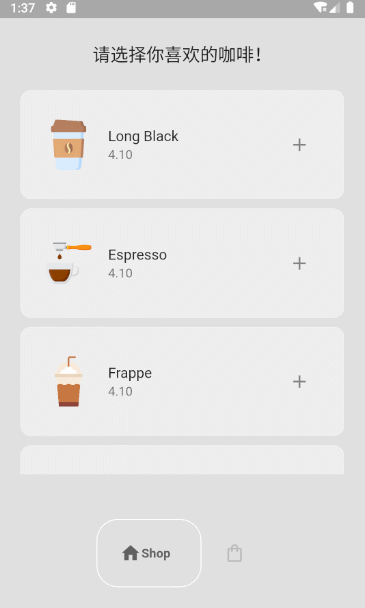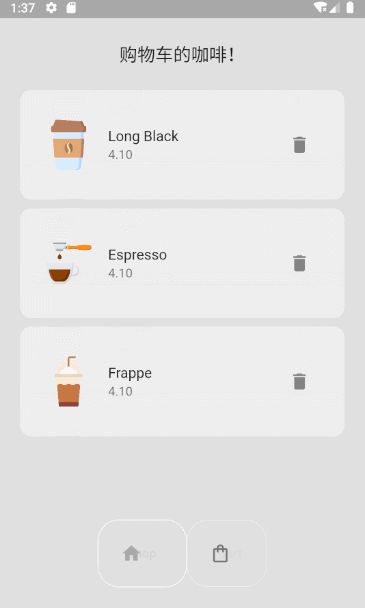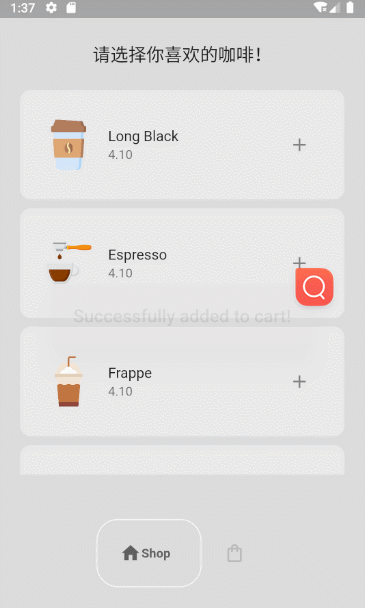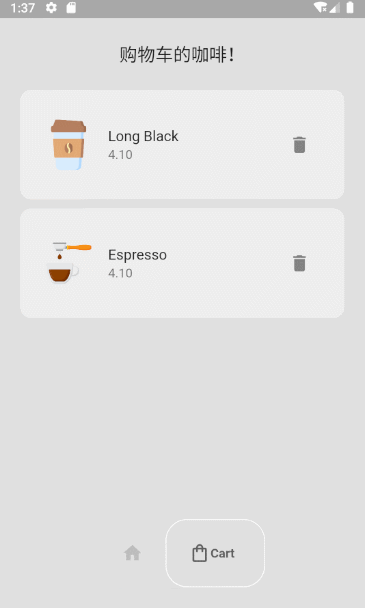
Flutter小功能实现-咖啡店
1 导航栏实现 效果图: 1.Package google_nav_bar: ^5.0.6 使用文档: google_nav_bar | Flutter Package 2.Code //MyBottomNavBar class MyBottomNavBar extends StatelessWidget {void Function(int)? onTabChange;MyBottomNavBar({super.key, …...

JavaSE 集合框架及背后的数据结构
目录 1 介绍2 学习的意义2.1 Java 集合框架的优点及作用2.2 笔试及面试题 3 接口 interfaces3.1 基本关系说明3.2 Collection 常用方法说明3.3 Collection 示例3.4 Map 常用方法说明3.5 Map 示例 4 实现 classes5 Java数据结构知识体系5.1 目标5.2 知识点 1 介绍 集合…...

-9501 MAL系统没有配置或者服务器不是企业版(dm8达梦数据库)
dm8达梦数据库 -9501 MAL系统没有配置或者服务器不是企业版) 环境介绍1 环境检查2 问题原因 环境介绍 搭建主备集群时,遇到报错-9501 MAL系统没有配置或者服务器不是企业版 1 环境检查 检查dmmal.ini配置文件权限正确 dmdba:dinstall,内容正…...

云备份——第三方库简单介绍并使用(上)
目录 一,Jsoncpp库序列化和反序列化 二,bundle文件压缩库 2.1 文件压缩 2.2 文件解压 一,Jsoncpp库序列化和反序列化 首先我们需要先了解一下json是什么,json是一种数据交换格式,采用完全独立于编程语言的文本格式来…...
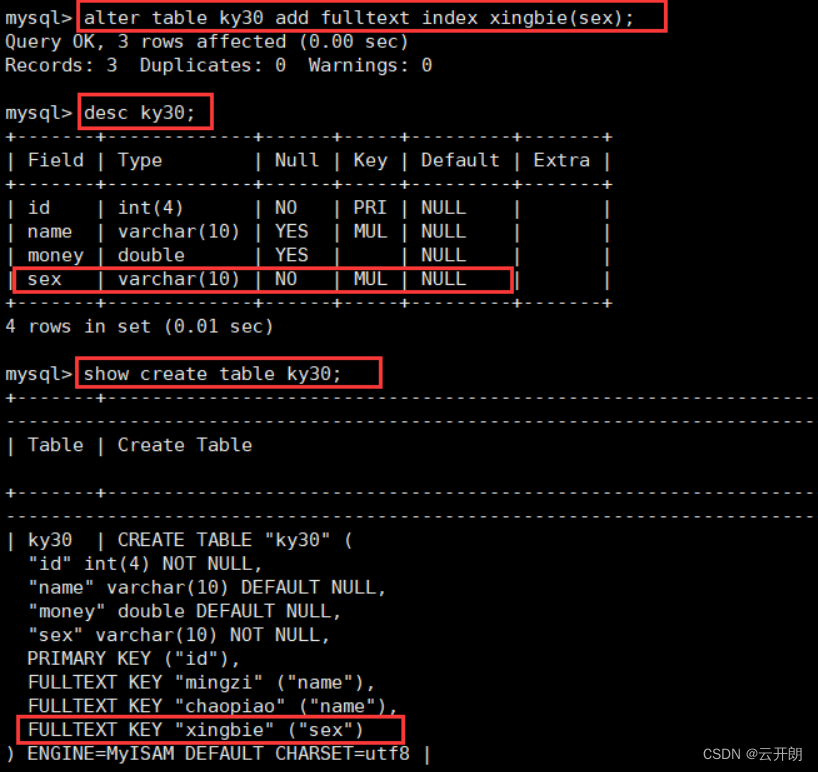
MySQL数据库之索引
目录 一、索引的概念 二、索引的作用 三、索引的副作用 四、创建索引的规则 1、适合创建为索引的字段的规则 2、MySQL的优化 哪些字段/场景适合创建索引,哪些不适合 五、索引的分类和创建 1、索引的分类 2、三种创建方式 3、索引的创建演示 1、创建普通索…...
:Mat支持的运算)
OpenCV(四):Mat支持的运算
目录 1.对两个 Mat 对象按元素进行运算,有加法、减法、乘法和除法等运算。 2.Mat类支持逻辑与、或、非等逻辑运算, 1.对两个 Mat 对象按元素进行运算,有加法、减法、乘法和除法等运算。 加法:Mat Mat,保存到 resul…...
WebRTC音视频通话-WebRTC推拉流过程中日志log输出
WebRTC音视频通话-WebRTC推拉流过程中日志log输出 之前实现iOS端调用ossrs服务实现推拉流流程。 推流:https://blog.csdn.net/gloryFlow/article/details/132262724 拉流:https://blog.csdn.net/gloryFlow/article/details/132417602 在推拉流过程中的…...

用Jmeter压测问题解决
最近做一个基于duboo服务的接口,需要进行稳定性测试。但是用Jmeter GUI 方式跑只能持续2个小时左右,Jmeter就崩溃了,日志报错:out of memory 解决方法如下: 直接运行jmeter的java包试试: 1、打开jmeter.…...

C语言:字符函数和字符串函数(一篇拿捏字符串函数!)
目录 求字符串长度: 1. strlen(字符串长度) 长度不受限制函数: 2. strcpy(字符串拷贝) 3. strcat(字符串追加) 4. strcmp(字符串比较) 长度受限制函数: 5. strncpy(字符串拷贝) 6. strncat(字符串追加) 7. strncmp(字符串比较) 字…...

问道管理:成交量买卖公式?
跟着股票商场的如火如荼,人们对于怎么解读和使用成交量进行股票生意的需求日积月累。成交量是指在某一特定时间内进行的股票生意的数量,它是投资者们研判商场状况和制定生意战略的重要指标之一。那么,是否存在一种最厉害的成交量生意公式呢&a…...

【MySQL】5、MySQL高阶语句
一、常用查询(增、删、改、查) 对 MySQL 数据库的查询,除了基本的查询外,有时候需要对查询的结果集进行处理。 例如只取 10 条数据、对查询结果进行排序或分组等等 模板表: 数据库有一张info表,记录了学生…...

【Linux】redhat7.8配置yum在线源【redhat7.8镜像容器内配置yum在线源】通用
👨🎓博主简介 🏅云计算领域优质创作者 🏅华为云开发者社区专家博主 🏅阿里云开发者社区专家博主 💊交流社区:运维交流社区 欢迎大家的加入! 🐋 希望大家多多支…...

强大的处理器和接口支持BL304ARM控制器
在智慧医疗领域,BL304可以用于实现医疗设备的智能化、远程监控和数据交换。在智慧电力领域,BL304可以帮助实现电网的智能化管理,提升电力供应的效率。在智慧安防领域,BL304可以实现智能监控、智能门锁等应用,保障安全。…...
react 基础知识(一)
1、 安装1 (版本 react 18) // 安装全局脚手架(create-react-app基于webpackes6) npm install -g create-react-app //使用脚手架搭建项目 create-react-app my-app // 打开目录 cd my-app // 运行项目 npm start2、初体验 impo…...

SpringBoot整合JUnit、MyBatis、SSM
🐌个人主页: 🐌 叶落闲庭 💨我的专栏:💨 c语言 数据结构 javaEE 操作系统 石可破也,而不可夺坚;丹可磨也,而不可夺赤。 SpringBoot整合 一、SpringBoot整合JUnit二、Spri…...
virtuoso61x中集成calibre
以virtuoso618为例,在搭建完电路、完成前仿工作之后绘制版图,版图绘制完成之后需要进行drc和lvs【仅对于学校内部通常的模拟后端流程而言】,一般采用mentor的calibre来完成drc和lvs。 服务器上安装有virtuoso和calibre,但是打开la…...

com.google.guava:guava 组件安全漏洞及健康分析
组件简介 维护者google组织许可证类型Apache-2.0首次发布2010 年 4 月 26 日最新发布时间2023 年 8 月 1 日GitHub Star48189GitHub Fork10716依赖包28,694依赖存储库219,576 Guava 是 Google 的一组核心 Java 库,其中包括新的集合类型(例如 multimap 和…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...

【WebSocket】SpringBoot项目中使用WebSocket
1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖,添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...
