【C++算法】dfs深度优先搜索(下) ——【全面深度剖析+经典例题展示】
💃🏼 本人简介:男
👶🏼 年龄:18
🤞 作者:那就叫我亮亮叭
📕 专栏:关于C/C++那点破事
文章目录
- 0.0 写在前面
- 1. 中国象棋
- 1.1 题干信息
- ① 背景说明概述
- ② 问题描述
- ③ 输入格式
- ④ 输出格式
- ⑤ 样例输入
- ⑥ 样例输出
- 1.2 思路解释
- 1.3 code展示
- 2. 踏青
- 2.1 题干信息
- ① 背景说明概述
- ② 问题描述
- ③ 输入格式
- ④ 输出格式
- ⑤ 样例输入
- ⑥ 样例输出
- 2.2 思路解释
- 2.3 code展示
- 3. 迷宫解的方案数
- 3.1 题干信息
- ① 背景说明概述
- ② 问题描述
- ③ 输入格式
- ④ 输出格式
- ⑤ 样例输入
- ⑥ 样例输出
- 3.2 思路解释
- 3.3 code展示
- 4. 最大的蛋糕块
- 4.1 题干信息
- ① 背景说明概述
- ② 问题描述
- ③ 输入格式
- ④ 输出格式
- ⑤ 样例输入
- ⑥ 样例输出
- 4.2 思路解释
- 4.3 code展示
- 5. 家谱
- 5.1 题干信息
- ① 背景说明概述
- ② 问题描述
- ③ 输入格式
- ④ 输出格式
- ⑤ 样例输入
- ⑥ 样例输出
- 5.2 思路解释
- 5.3 code展示
- 最后,感谢大家支持u (^ _ ^)
0.0 写在前面
书接上文,上次我们讲到了深搜的思想与经典的迷宫问题,这次我们不再细节性讲解其思想,重在针通过几道例题来实践掌握深搜的用法,欢迎大佬们来指点一二,我们一起加油!!还没了解的可以直接点进行学习哦👉👉👉【C++算法】dfs深度优先搜索(上) ——【全面深度剖析+经典例题展示】
1. 中国象棋
1.1 题干信息
① 背景说明概述
中国象棋博大精深,其中
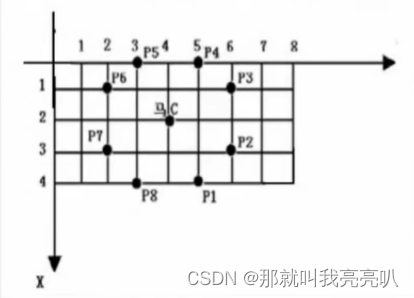
马的规则最为复杂,也是最难操控的一颗棋子。我们都知道象棋中马走"日",比如在(2, 4)位置的一个马【如下图所示】,跳一步能到达的位置有(0,3),(0,5),(1,2),(1,6),(3,2),(3,6),(4,3),(4,5)。
- 注意:上图中,竖直向下的是x,水平向右的是y!!!
② 问题描述
蒜头君正在和花椰妹下棋,蒜头君正在进行战略布局,他需要把在(x, y)位置的马跳到(x’,
y’)位置,以达到威慑的目的。但是棋盘大小有限制,棋盘是一个10 x 9的网格,左上角坐标为(0,0),右下角坐标为(9,
8),马不能走出棋盘,并且有些地方已经有了棋子,马也不能跳到有棋子的点。蒜头君想知道,在不移动其他棋子的情况下,能否完成他的战略目标。
③ 输入格式
- 输入一共10行,每行一个长度为9的字符串。
- 输入表示这个棋盘,我们用
'.'表示空位置,用'#'表示该位置有棋子,用'S'表示初始的马的位置,用'T'表示马需要跳到的位置。 - 输入保证一定只有一个
'S'和'T'。
④ 输出格式
如果在不移动其他棋子的情况下,马能从'S'跳到'T',那么输出一行"Yes",否则输出一行"No"。
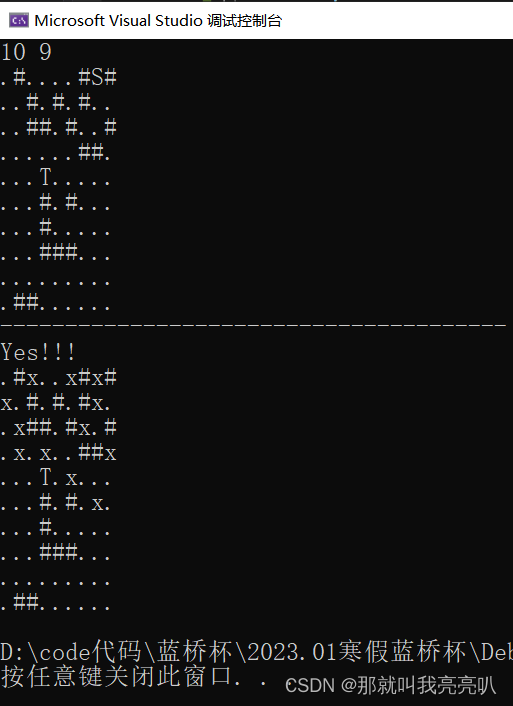
⑤ 样例输入
.#....#S#
..#.#.#..
..##.#..#
......##.
...T.....
...#.#...
...#.....
...###...
.........
.##......
⑥ 样例输出
Yes
1.2 思路解释
和上一篇例题的思路基本一模一样,只不过上次迷宫只能是上下左右走,而这次的象棋中🐎可以走八个方向,只是对x、y坐标的改变不同而已,其他基本一致,所以这里就不过多赘述了,不太明白的可以点这里哦【C++算法】dfs深度优先搜索(上) ——【全面深度剖析+经典例题展示】
大致思路如下:
- ①判断象棋终点,记录所走路径
- ②完善搜索回溯,处理数组边界
- ③找寻马儿起点,打印结束路径
1.3 code展示
#include<iostream>
#include<stdio.h>
using namespace std;int n, m;
char pos[105][105];
int trace[105][105];
int dir[8][2] = { {-1 , -2} , {-2 , -1} , {-2 , 1} , {-1 , 2} , {1 , 2} , {2 , 1} , {2 , -1} , {1 , -2} }; // 找出马儿走"日"时x、y坐标变化的所有情况【基本按逆时针来】bool check_in(int x, int y) { // 判断数组是否越界return (x >= 1 && x <= n && y >= 1 && y <= m); //这里表示的是如果()里为真,则返回true,否则返回false
}bool dfs(int x, int y) {if (pos[x][y] == 'T') {return true;}pos[x][y] = 'x'; //用x记录路径trace[x][y] = 1; //标记已走过for (int i = 0; i < 8; i++) {int xx = x + dir[i][0]; //表示x加上第几个方向的第1个数,即变化后行的坐标int yy = y + dir[i][1]; //表示y加上第几个方向的第2个数,即变化后列的坐标if (pos[xx][yy] != '#' && check_in(xx, yy) && !trace[xx][yy]) {if (dfs(xx , yy)) {return true;} }} pos[x][y] = '.'; // 如果一个位置的上下左右都走不了,则取消该位置的路径进行回溯,回溯过程把之前已标记的'x'改回'.'trace[x][y] = 0; //走不通,则回溯过程标记为没走过return false;
}int main() {cin >> n >> m;//输入象棋地图 找🐎儿的起点int x , y;for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {cin >> pos[i][j];if (pos[i][j] == 'S') {x = i, y = j;}}}cout << "--------------------------------" << endl;if (dfs(x , y)) {cout << "Yes!!!" << endl;for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {cout << pos[i][j];} cout << endl;}}else {cout << "No!!!" << endl;}return 0;
}
2. 踏青
2.1 题干信息
① 背景说明概述
蒜头君和他的朋友周末相约去召唤师峡谷踏青。他们发现召唤师峡谷的地图是由
一块一块格子组成的,有的格子上是草丛,有的是空地。草丛通过上下左右4个方向扩展其他草丛形成一片草地,任何一片草地中的格子都是草丛,并且所有格子之间都能通过上下左右连通。如果用'#"代表草丛,'.'代表空地,则下面的峡谷中有2片草地。
##..
..##
② 问题描述
- 处在
同一个草地的2个人可以相互看到,空地看不到草地里面的人。他们发现有一个朋友不见了,现在需要分头去找,每个人负责一片草地,蒜头君想知道他们至少需要多少人。
③ 输入格式
- 第一行输入n,m(1 ≤ n, m <= 100) 表示峡谷大小。接下来输入n行字符串表示峡谷的地形。
④ 输出格式
- 输出至少需要多少人。
⑤ 样例输入
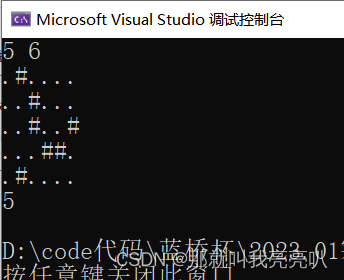
5 6
.#....
..#...
..#..#
...##.
.#....
⑥ 样例输出
5
2.2 思路解释
- 根据题意,最后要求
最少人数,而根据一人负责一片草地,则就转换求最少草地数,就是该地形最少有多少片土地。我们先输入地形,再依次遍历每个格子是否为草地,如果不是草地,直接略过;如果是草地,则是否之前找过,如果找过则还是略过,如果没找过,则先记录下已找过,结果+1,并对该草地的上下左右遍历是否是未被找的草地【深搜思想】。最后输出结果。
2.3 code展示
#include<iostream>
#include<stdio.h>
using namespace std;int n, m, ans = 0;
char pos[105][105];
bool trace[105][105];//法一
//bool check_in(int x, int y) {
// return (x >= 1 && x <= n && y >= 1 && y <= m);
//}
//
//void dfs(int x, int y) {
// if (check_in(x, y) && pos[x][y] == '#' && !trace[x][y]) {
// trace[x][y] = 1;
// dfs(x, y + 1);
// dfs(x + 1, y);
// dfs(x, y - 1);
// dfs(x - 1, y);
// }
//}//法二
void dfs(int x, int y) {if (x < 1 || x > n || y < 1 || y > m || trace[x][y] || pos[x][y] == '.') {return;}trace[x][y] = true;dfs(x - 1, y); //记录上面dfs(x , y - 1); //记录左面dfs(x + 1, y); // 记录下面dfs(x , y + 1); //记录右面
}int main() {cin >> n >> m;for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {cin >> pos[i][j];}}for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {if (!trace[i][j] && pos[i][j] == '#') { // 假如是草丛的话且之前没找过dfs(i, j); // 把这个位置和周边草丛标记好ans++; //记录草丛数量}}}cout << ans << endl;return 0;
}
3. 迷宫解的方案数
3.1 题干信息
① 背景说明概述
蒜头君是一个玩迷宫的高手,天下还没有能难住他的迷宫。但是总有人喜欢习难蒜头君,不停的给蒜头君出难题。这个出题的人很聪明,他知道天下还没有能难住蒜头君的迷宫。
② 问题描述
- 所以他便转换思维问蒜头君,在
不走重复路径的情况下,总共有多少不同可以到达终点的路径呢?蒜头君稍加思索便给出了答案,你要不要也来挑战一下?
③ 输入格式
- 第一行输入两个整数
n(1≤n≤11),m(1≤m≤11), 表示迷宫的行和列。然后有一个n*m的地图,地图由'.'、'#'、's'、'e'这四个部分组成。'.'表示可以通行的路,'#'表示迷宫的墙,'s'表示起始点,'e'表示终点。
④ 输出格式
- 输出一个整数,表示从
's'到达'e'的所有方案数。
⑤ 样例输入
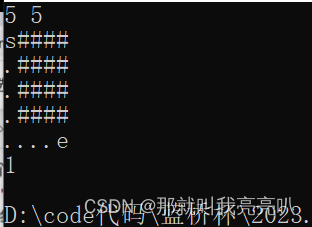
5 5
s####
.####
.####
.####
....e
⑥ 样例输出
1
3.2 思路解释
- 本题和前面迷宫例题思路差不多,但这个题是要统计到终点的路线的个数,所以如果能到终点,则需要ans++;如果该节点的上下左右都行不通,则在四周判断完后需要
清空路径,trace[x][y]=0,来继续探索下一条路。
3.3 code展示
#include<iostream>
#include<stdio.h>
using namespace std;int n, m, ans = 0;
char pos[105][105];
bool trace[105][105];
int dir[4][2] = { {-1, 0},{0,-1},{1,0},{0,1} };bool check_in(int x, int y) {return (x >= 1 && x <= n && y >= 1 && y <= m);
}void dfs(int x, int y) {if (pos[x][y] == 'e') {ans++; //节点为终点,所以找到一条走到终点的路,ans++;return ;}if (check_in(x, y) && pos[x][y] != '#' && !trace[x][y]) { //如果这个节点不是终点且没越界,不是墙且没走过,则统计四周情况trace[x][y] = 1;for (int i = 0; i < 4; i++) {int xx = x + dir[i][0];int yy = y + dir[i][1];dfs(xx, yy);}trace[x][y] = 0; //清空路线,找下一条路}
}int main() {cin >> n >> m;int x, y;for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {cin >> pos[i][j];if (pos[i][j] == 's') {x = i, y = j;}}}dfs(x, y);cout << ans << endl;return 0;
}
4. 最大的蛋糕块
4.1 题干信息
① 背景说明概述
这一天蒜头君生日,他的朋友们一起来给蒜头君买一个大的蛋糕过生日。游戏做完后到了切蛋糕的时刻了,朋友们知道蒜头君喜欢吃蛋糕,便让蒜头君自己给自己切-块最大的。蒜头君看朋友们这么热情也就不客气了。
② 问题描述
- 这块蛋糕是由
R*C的网格构成,每个网格上面都放有不同的水果。蒜头君把这些水果分为两类,一类是自己喜欢吃的水果,用'#'来表示;一类是自己不喜欢吃的水果,用'.'来表示。 - 蒜头君对切出的蛋糕有如下要求:
- 切出的蛋糕连成一块(可以不为矩形,但必须在网格上连通)
- 切出的蛋糕只包含自己喜欢吃的水果
- 请问,蒜头君最大可以吃到多大的蛋糕?
③ 输入格式
- 第一行输入两个被空格隔开的整数
R(1≤R≤1000)和C(1≤C≤1000)。然后会有一个R*C的网格,由'#'和'.'组成。
④ 输出格式
- 输出一个整数,表示蒜头君可以吃到的蛋糕最大是多少(即对应到网格中的格子数)。
⑤ 样例输入
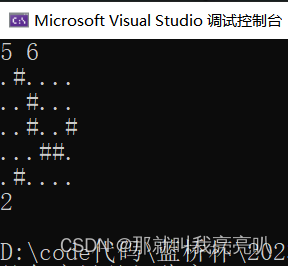
5 6
.#....
..#...
..#..#
...##.
.#....
⑥ 样例输出
2
4.2 思路解释
和题2《踏青》的总体思路一样,但《踏青》求的是带'#'每部分的数量,而本题是求每部分里'#'最多的数量。所以这道题只需要在统计每部分时记录'#'的数量再进行比较即可。
4.3 code展示
#include<iostream>
#include<stdio.h>
using namespace std;int r, c, ans = 0, cnt = 0;
char pos[105][105];
bool trace[105][105];
int dir[4][2] = { {-1, 0},{0,-1},{1,0},{0,1} };bool check_in(int x, int y) {return (x >= 1 && x <= r && y >= 1 && y <= c);
}void dfs(int x, int y) {if (!check_in(x, y) || pos[x][y] != '#' || trace[x][y]) { //深搜过程中不合要求的返回;return;}trace[x][y] = 1; //标记访问过cnt++; //记录数量for (int i = 0; i < r; i++) {int xx = x + dir[i][0];int yy = y + dir[i][1];if (pos[xx][yy] == '#') {dfs(xx, yy);}}
}int main() {cin >> r >> c;int x, y;for (int i = 1; i <= r; i++) {for (int j = 1; j <= c; j++) {cin >> pos[i][j];}}for (int i = 1; i <= r; i++) {for (int j = 1; j <= c; j++) {if (!trace[i][j] && pos[i][j] == '#') { //如果是'#',且之前没被访问过,则用dfs记录下cnt = 0; //需要将该位置能求到的数量重置为0dfs(i, j); //用dfs求一下所有‘#’的数量if (ans < cnt) {ans = cnt; //更新一下ans}}}}cout << ans << endl;return 0;
}
5. 家谱
5.1 题干信息
① 背景说明概述
家谱,又称族谱、宗谱等,是一种以表谱形式,记载一个家族的世系繁衍及重要人物事迹的书。皇帝的家谱称玉牒,如新朝玉牒、皇宋玉牒。它以记载父系家族世系、人物为中心,由正史中的帝王本纪及王侯列传、年表等演变而来。家谱是一种特殊的文献,就其内容而言,是中国五千年文明史中具有平民特色的文献,记载的是同宗共祖血缘集团世系人物和事迹等方面情况的历史图籍。家谱属珍贵的人文资料,对于历史学、民俗学、人口学、社会学和经济学的深入研究,均有其不可替代的独特功能。
② 问题描述
- 这一天蒜头君拿到了自己家的家谱,蒜头君便想知道,在自己家的家谱中,每位祖先有多少直系后代(
直系后代包括他的孩子和他孩子的直系后代)。但是家族历史源远流长,家谱实在太庞大了,自己一个人完全数不过来。热心的你便自告奋勇帮蒜头君写一个程序,来统计每位祖先有多少直系后代。
③ 输入格式
- 输入的第一行有一个整数
n(1<n≤100000),表示家谱中的总人数。接下来读入n- 1行,每行有两个整数x(1≤x≤n),y(1≤y≤n),表示x是y的父母。
④ 输出格式
- 输出n行,每行有一个整数,表示第i个人有多少个直系后代。
⑤ 样例输入
4
1 2
1 3
2 4
⑥ 样例输出
3
1
0
0
5.2 思路解释
本题输入数值的大小不确定,所以如果指定数组大小,则可能报错,所以我们采用动态数组vector来统计son数量。所以首先,我们先找根节点,所以要找直系儿子,则需要把所有儿子的后代标记一下,最后未被标记的就是直系儿子。我们找到根节点,需要先对根节点的后代进行搜索,直到找到答案。
5.3 code展示
#include<iostream>
#include<stdio.h>
#include<vector>
using namespace std;
const int N = 1e5 + 10;int n, x, y, u;
vector<int> son[N]; //使用动态数组,便于插入和删除
bool judge_son[N]; //判断是否是儿子
int ans[N];int dfs(int a) { // 找有多少个直系后代【不包括自己】,但统计时为了方便,则统计自己int cnt = 0;int len = son[a].size();for (int i = 0; i < len; i++) { //首先,找根节点的后代cnt += dfs(son[a].at(i)); //找根节点的直接后代,或者写dfs(son[u][i])}ans[u] = cnt; //统计后代个数return cnt + 1; //加上自己
}int main() {cin >> n;for (int i = 1; i < n; i++) {cin >> x >> y; //输入x,y 表示x是y的父亲son[x].push_back(y); //将y放入son[x]的动态数组中judge_son[y] = true; //y已经作为儿子了,所以标为true;}for (int i = 1; i <= n; i++) { //找起始位置,即找“根”节点if (!judge_son[i]) { //找到赋给u,并breaku = i;break;}}dfs(u);for (int i = 1; i <= n; i++) {cout << ans[i] << endl;}return 0;
}
最后,感谢大家支持u (^ _ ^)
如果感觉这篇文章对你有帮助的话,不妨三连支持下,十分感谢(✪ω✪)。
printf("点个赞吧*^*");
cout << "收藏一下叭o_o";
System.out.println("评论一下吧^_^");
print("关注一下叭0-0")
相关文章:

【C++算法】dfs深度优先搜索(下) ——【全面深度剖析+经典例题展示】
💃🏼 本人简介:男 👶🏼 年龄:18 🤞 作者:那就叫我亮亮叭 📕 专栏:关于C/C那点破事 文章目录0.0 写在前面1. 中国象棋1.1 题干信息① 背景说明概述② 问题描述…...
HIVE 基础(三)
目录 建表语句 表数据 Hive建表高阶语句 - CTAS and WITH CTAS – as select方式建表 CTE (CTAS with Common Table Expression) LIKE 创建临时表 清空表数据 修改表(Alter针对元数据) 改名 修正表文件格式 修改列名 添加列 替换列 动态分…...

redis-cluster集群搭建
安装redis所需环境 yum install -y gcc-c yum install -y wget 创建文件夹 cd / mkdir redis/redis-cluster/7001 cd redis/redis-cluster mkdir 7002 7003 7004 7005 7006 7007 7008下载redis压缩包并解压安装 wget https://download.redis.io/redis-stable.tar.gz tar -…...

【C语言】可变参数列表va_list
本篇博客让我们来认识一下C语言学习过程中往往被忽略的可变参数列表 所谓可变参数,就是一个不限定参数数量的函数,我们可以往里面传入任意个数的参数,以达成某些目的。 关联:C11可变模板参数 1.函数 #include <stdarg.h>…...
CentOS7.6 MySQL8安装
1 检查是否安装过 MySQL rpm -qa | grep -i mysqlmariadb rpm -qa | grep mariadb2 卸载之前的安装 MySQL rpm -e --nodeps 软件名 //强力删除,对相关依赖的文件也进行强力删除卸载 rpm -e --nodeps mariadb-libs-5.5.60-1.el7_5.x86_643 官网下载 MySQL :: D…...

安装Tomcat的步骤?
首先先完成JDK配置,javac -version 检测 1.把tomcat下载到本地硬盘 2.创建tomcat8.0文件夹,完成解压(免安装)4.打开解压之后的目录,进入bin目录,双击startup.bat,启动tomcat5.可以看到弹出一个黑色的窗口,不要关闭,如果关闭意味着…...

Redis之分布式锁
随着业务发展的需要,原单体单机部署的系统被演化成分布式集群系统后,由于分布式系统多线程、多进程并且分布在不同机器上,这将使原单机部署情况下的并发控制锁策略失效,单纯的 Java API并不能提供分布式锁的能力。为了解决这个问题…...

2022年中国前10电商GMV总结
我是卢松松,点点上面的头像,欢迎关注我哦! 1,阿里8万亿;2,京东3万亿;3,拼多多3万亿;4,小程序私域电商3万亿;5,抖音电商1.4万亿。6,抖音本地生活服务电商600亿。7…...

ES6新增扩展:字符串-数值-数组-函数-对象
ES6新增扩展字符串的扩展判断字符串是否包含在另一个字符中字符串补全字符串重复消除字符串空格replaceAll()替换全部字符串at字符串匹配输出数值的扩展数值分隔符检测数值是否有限检测是否为NaNNumber.parseInt()、Number.parseFloat()isInteger()判断是否为整数Math.sign()判…...

python中import原理
0. 前言 在 python 中引入 Module 是再常见不过了,那么当我们 import 时它做了什么事情呢?它是如何加载 Module 使用的呢? 1. 什么是 module? 一般,Module 是一个后缀为 .py 的文件,其 module 名称一般…...
《Qt6开发及实例》6-4 显示SVG格式图片
目录 一、简介与设计 1.1 简介 1.2 设计 二、SvgWidget 2.1 鼠标滚轮事件 三、svgwindow 四、MainWindow 一、简介与设计 1.1 简介 1、SVG 的英文全称是 Scalable Vector Graphics,即可缩放的矢量图形。它是由万维网联盟(W3C)在 200…...
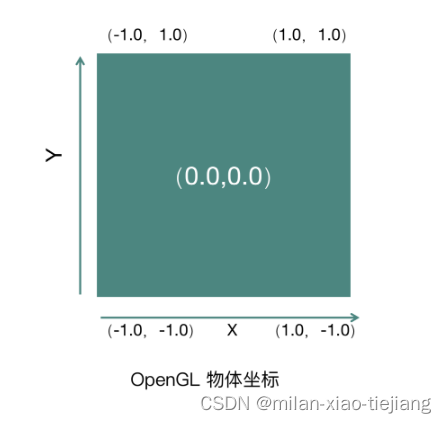
OpenGL ES 绘制一张图片
GLSL 语法与内建函数 GLSL 的修饰符与数据类型 GLSL 中变量的修饰符 const:修饰不可被外界改变的常量attribute:修饰经常更改的变量,只可以在顶点着色器中使用uniform:修饰不经常更改的变量,可用于顶点着色器和片段…...

Python 之 Pandas DataFrame 数据类型的行操作和常用属性和方法汇总
文章目录一、DataFrame 行操作1. 标签选取2. 数值型索引和切片3. 切片操作多行选取4. 添加数据行4.1 追加字典4.2 追加列表5. 删除数据行二、常用属性和方法汇总1. 转置2. axes3. dtypes4. empty5. columns6. shape7. values8. head() & tail()9. 修改列名 rename()10. inf…...

MacOS下载钉钉直播回放视频的Python最新解决方案
tags: Python MacOS Tips 写在前面 之前写过一篇关于用Charles抓包下载钉钉直播回放视频的方法, 那会还是可以直接通过FFmpeg下载m3u8链接并且直接合并的, 但是现在直接上FFmpeg会出现403, 所以还是用别的方法来做吧. 后来发现抓包找到的m3u8不是加密视频流, 那就直接下载ts…...
2023年测试人跳槽新功略,涨薪10K+
软件测试是如何实现涨薪的呢?很多人眼中的软件测试岗位可能是简单的,技术含量不是那么高,就是看看需求、看业务、设计文档、然后点一点功能是否实现,再稍微深入一点就是测试下安装部署时会不会出现兼容性问题,以及易用…...
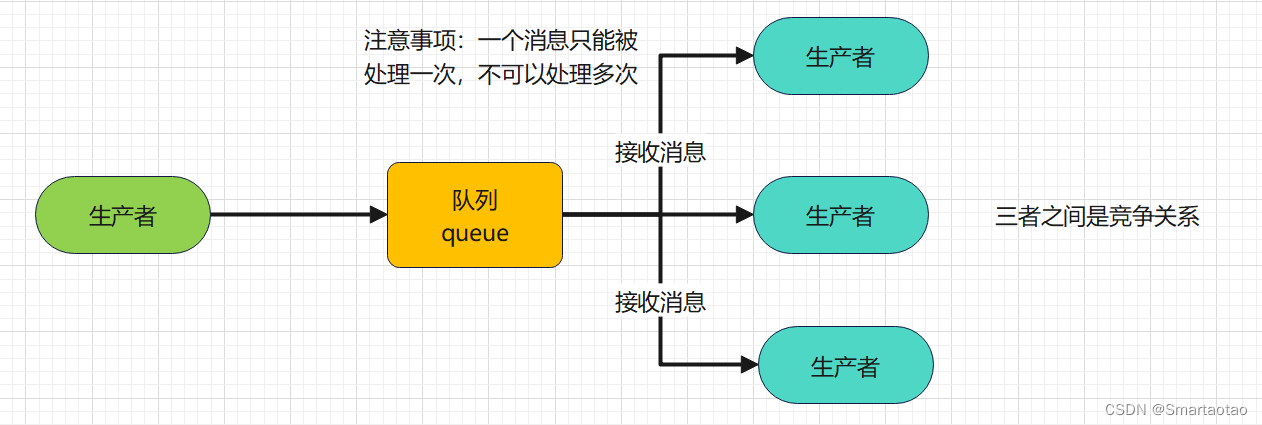
RabbitMQ之Work Queues
Work Queues 工作队列(又称任务队列)的主要思想是避免立即执行资源密集型任务,而不得不等待它完成。相反我们安排任务在之后执行。我们把任务封装为消息并将其发送到队列。在后台运行的工作进程将弹出任务并最终执行作业。当有多个工作线程时,这些工作线程将一起处理这些任务…...
CRM哪家好?这5个CRM管理系统很好用!
CRM哪家好?这5个CRM管理系统很好用! CRM(Customer Relationship Management)即客户关系管理,能够帮助提高客户的价值、满意度、赢利性和忠实度,缩减销售周期和销售成本、增加收入、寻找扩展业务所需的新的市场和渠道,…...

国内ce认证机构有哪些 国内十大CE认证机构排名 做ce认证的公司推荐
CE认证,是任何企业的任何产品走进欧盟市场的硬性要求。挑选CE认证机构,一定要认准拥有正规资质的机构/企业,例如中国质量认证中心CQC、CVC威凯、CTI华测检测,以及TV南德认证、安博检测、万泰认证等。本文中,MaiGoo小编…...

多If函数封装的策略
在工作中我们经常遇到有多个if的判读函数,这是一件很正常的事情,如下: let order function (orderType, isPay, count) {if (orderType 1) {// 充值 500if (isPay true) {// 充值成功console.log(中奖100元)} else {if (count > 0) {c…...

238. 银河英雄传说
Powered by:NEFU AB-IN Link 文章目录238. 银河英雄传说题意思路代码238. 银河英雄传说 题意 有一个划分为 N列的星际战场,各列依次编号为 1,2,…,N 有 N艘战舰,也依次编号为 1,2,…,N,其中第 i号战舰处于第 i列。 有 T条指令,每…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...

FFmpeg avformat_open_input函数分析
函数内部的总体流程如下: avformat_open_input 精简后的代码如下: int avformat_open_input(AVFormatContext **ps, const char *filename,ff_const59 AVInputFormat *fmt, AVDictionary **options) {AVFormatContext *s *ps;int i, ret 0;AVDictio…...

Monorepo架构: Nx Cloud 扩展能力与缓存加速
借助 Nx Cloud 实现项目协同与加速构建 1 ) 缓存工作原理分析 在了解了本地缓存和远程缓存之后,我们来探究缓存是如何工作的。以计算文件的哈希串为例,若后续运行任务时文件哈希串未变,系统会直接使用对应的输出和制品文件。 2 …...

AWS vs 阿里云:功能、服务与性能对比指南
在云计算领域,Amazon Web Services (AWS) 和阿里云 (Alibaba Cloud) 是全球领先的提供商,各自在功能范围、服务生态系统、性能表现和适用场景上具有独特优势。基于提供的引用[1]-[5],我将从功能、服务和性能三个方面进行结构化对比分析&#…...