第七章,相似矩阵及其应用,3-二次型、合同矩阵与合同变换
第七章,相似矩阵及其应用,3-二次型、合同矩阵与合同变换
- 二次型相关概念
- 二次型
- 二次型的标准形和规范形
- 表示形式
- 合同矩阵与合同变换
- 定义 合同
- 合同矩阵的性质
- 等价、相似、合同三种关系的对比
- 等价
- 相似
- 合同
玩转线性代数(38)二次型概念、合同矩阵与合同变换的笔记,相关证明以及例子见原文
二次型相关概念
二次型
含有n个变量 x 1 , x 2 , . . . x n x_1,x_2,...x_n x1,x2,...xn的二次齐次函数:
f ( x 1 , x 2 , . . . x n ) = a 11 x 1 2 + a 22 x 2 2 + . . . + a n n x n 2 + 2 a 12 x 1 x 2 + 2 a 13 x 1 x 3 + . . . + 2 a n − 1 , n x n − 1 x n f(x_1,x_2,...x_n)=a_{11}x_1^2+a_{22}x_2^2+...+a_{nn}x_n^2+2a_{12}x_1x_2+2a_{13}x_1x_3+...+2a_{n-1,n}x_{n-1}x_n f(x1,x2,...xn)=a11x12+a22x22+...+annxn2+2a12x1x2+2a13x1x3+...+2an−1,nxn−1xn
称为二次型。
二次型的标准形和规范形
f = k 1 y 1 2 + k 2 y 2 2 + . . . + k n y n 2 f=k_1y_1^2+k_2y_2^2+...+k_ny_n^2 f=k1y12+k2y22+...+knyn2
这种只含平方项的二次型,称为二次型的标准形。
如果二次型的标准形形如:
f = y 1 2 + . . . + y p 2 − y p + 1 2 − . . . − y r 2 f = y_1^2+...+y_p^2-y_{p+1}^2-...-y_r^2 f=y12+...+yp2−yp+12−...−yr2
即系数只有-1,1,0三个取值,称为二次型的规范形。
表示形式
f ( x 1 , x 2 , . . . x n ) = a 11 x 1 2 + a 22 x 2 2 + . . . + a n n x n 2 + 2 a 12 x 1 x 2 + 2 a 13 x 1 x 3 + . . . + 2 a n − 1 , n x n − 1 x n f(x_1,x_2,...x_n)=a_{11}x_1^2+a_{22}x_2^2+...+a_{nn}x_n^2+2a_{12}x_1x_2+2a_{13}x_1x_3+...+2a_{n-1,n}x_{n-1}x_n f(x1,x2,...xn)=a11x12+a22x22+...+annxn2+2a12x1x2+2a13x1x3+...+2an−1,nxn−1xn
取 a i j = a j i a_{ij}=a_{ji} aij=aji(对称矩阵),则 2 a i j x i x j = a i j x i x j + a j i x j x i 2a_{ij}x_ix_j=a_{ij}x_ix_j+a_{ji}x_jx_i 2aijxixj=aijxixj+ajixjxi,于是
f = ∑ i , j = 1 n a i j x i x j = ( x 1 , x 2 , . . . , x n ) ( a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋯ ⋯ ⋯ ⋯ a n 1 a n 2 ⋯ a n n ) ( x 1 x 2 ⋮ x n ) = x T A x f=\sum_{i,j=1}^na_{ij}x_ix_j = (x_1,x_2,...,x_n)\begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \cdots & \cdots & \cdots & \cdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{pmatrix}\begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix}=x^TAx f=i,j=1∑naijxixj=(x1,x2,...,xn) a11a21⋯an1a12a22⋯an2⋯⋯⋯⋯a1na2n⋯ann x1x2⋮xn =xTAx
把对称矩阵A叫做二次型f的矩阵,f叫做对称矩阵A的二次型,对称矩阵A的秩叫做二次型f的秩
合同矩阵与合同变换
设有可逆线性变换x=Cy,将x=Cy代入 f = x T A x f=x^TAx f=xTAx,有
f = = x T A x = ( C y ) T A ( C y ) = y T ( C T A C ) y = y T B y f==x^TAx=(Cy)^TA(Cy)=y^T(C^TAC)y=y^TBy f==xTAx=(Cy)TA(Cy)=yT(CTAC)y=yTBy
理解:线性变换后,将向量的坐标由x变换为了y,令原坐标系为 E = ( e 1 , e 2 , . . . , e n ) E=(e_1,e_2,...,e_n) E=(e1,e2,...,en),变换之后, E C = C EC=C EC=C,过渡矩阵为C,则新基为 C = ( c 1 , c 2 , . . . , c n ) C=(c_1,c_2,...,c_n) C=(c1,c2,...,cn),向量在新基下的坐标为y, y = C − 1 x y=C^{-1}x y=C−1x是坐标变换公式
定义 合同
设A与B为n阶方阵,若有可逆矩阵C,使 B = C T A C B=C^TAC B=CTAC,则称矩阵A与B合同
本质:是同一个二次型在不同基下的矩阵,对比相似矩阵,相似矩阵是同一个线性变换在不同基下的表示矩阵,合同矩阵首先都是对称的,又因 B = C T A C B=C^TAC B=CTAC,C可逆,故合同矩阵又是等价的。
合同矩阵的性质
(1)自反性 任意方阵A与其自身合同: E T A E = A E^TAE=A ETAE=A
(2)对称性 若A与B合同,则B与A合同:若A与B合同,则存在可逆阵C使得 C T A C = B C^TAC=B CTAC=B,则 A = ( C T ) − 1 B ( C − 1 ) = ( C − 1 ) T B ( C − 1 ) A=(C^T)^{-1}B(C^{-1})=(C^{-1})^TB(C^{-1}) A=(CT)−1B(C−1)=(C−1)TB(C−1),即B与A合同
(3)传递性 若A与B合同,B与C合同,则A与C合同:由 B = C 1 T A C 1 , C = C 2 T B C 2 B=C_1^TAC_1,C=C_2^TBC_2 B=C1TAC1,C=C2TBC2,得 C = C 2 T ( C 1 T A C 1 ) C 2 = ( C 1 C 2 ) T A ( C 1 C 2 ) C=C_2^T(C_1^TAC_1)C_2=(C_1C_2)^TA(C_1C_2) C=C2T(C1TAC1)C2=(C1C2)TA(C1C2),故A与C合同。
等价、相似、合同三种关系的对比
等价
A经过若干次初等行变换或初等列变换得到B,则A与B等价 ⇔ \Leftrightarrow ⇔ 存在可逆阵P,A,使 P A Q = B PAQ=B PAQ=B成立
相似
A与B相似 ⇔ \Leftrightarrow ⇔存在可逆阵P,使 P − 1 A P = B P^{-1}AP=B P−1AP=B。(同一个线性变换在不同基下的表示矩阵)
合同
A与B合同 ⇔ \Leftrightarrow ⇔存在可逆阵P,使 P T A P = B P^TAP=B PTAP=B。(同一个二次型在不同可逆线性变换下的矩阵)
通过以上三个定义可以看出,相似矩阵一定是等价矩阵,合同矩阵一定是等价矩阵.但等价矩阵不一定是相似矩阵,也不一定是合同矩阵.
相关文章:

第七章,相似矩阵及其应用,3-二次型、合同矩阵与合同变换
第七章,相似矩阵及其应用,3-二次型、合同矩阵与合同变换 二次型相关概念二次型二次型的标准形和规范形表示形式 合同矩阵与合同变换定义 合同合同矩阵的性质等价、相似、合同三种关系的对比等价相似合同 玩转线性代数(38)二次型概念、合同矩阵与合同变换…...

css学习7(盒子模型)
1、盒子模型图: Margin(外边距) - 清除边框外的区域,外边距是透明的。Border(边框) - 围绕在内边距和内容外的边框。Padding(内边距) - 清除内容周围的区域,内边距是透明的。Content(内容) - 盒子的内容,显示文本和图像。 <!DO…...
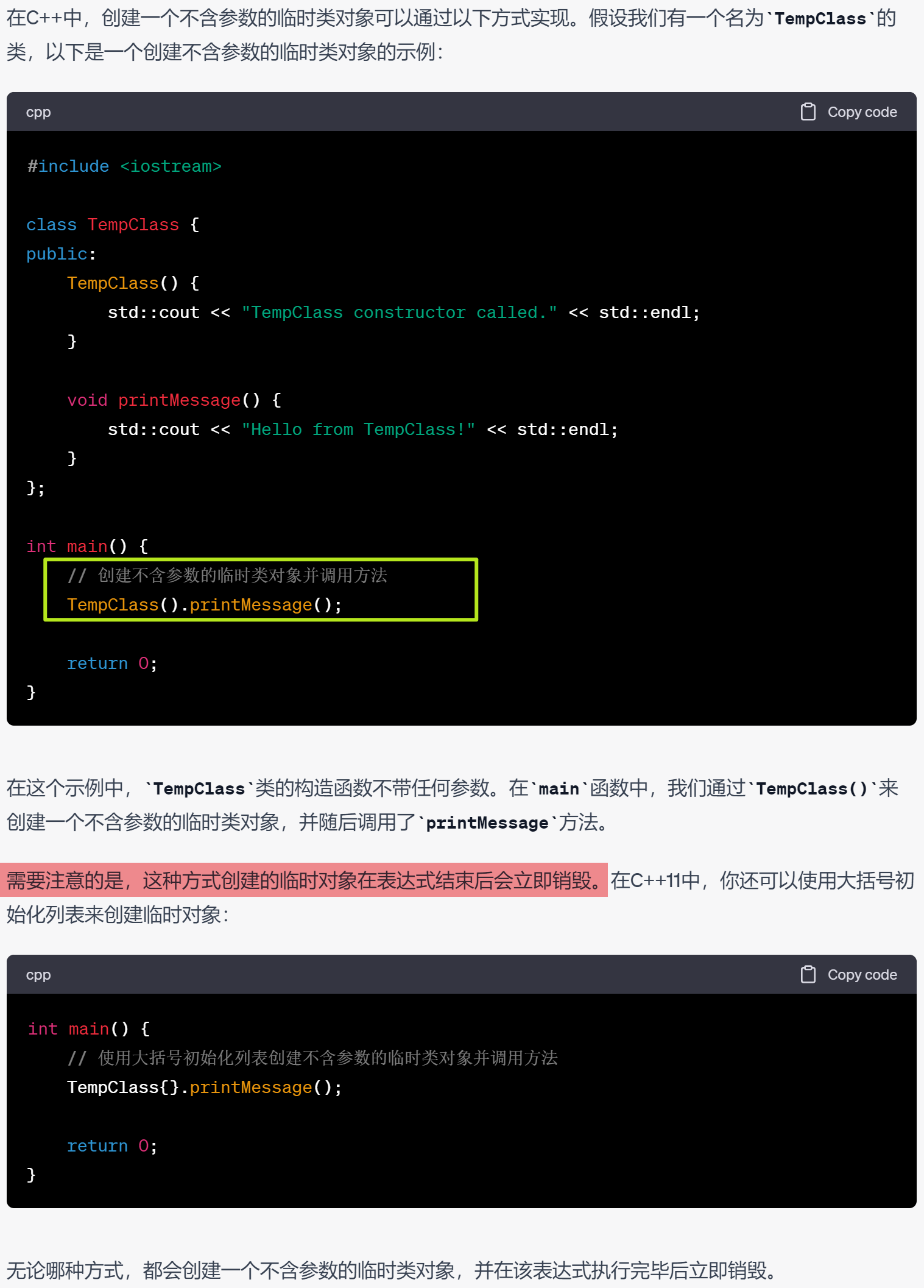
C++笔记之临时变量与临时对象与匿名对象
C笔记之临时变量与临时对象与匿名对象 code review! 文章目录 C笔记之临时变量与临时对象与匿名对象1.C中的临时变量指的是什么?2.C中的临时对象指的是什么?3.C中临时对象的作用是什么?什么时候要用到临时对象?4.给我列举具体的例子说明临…...
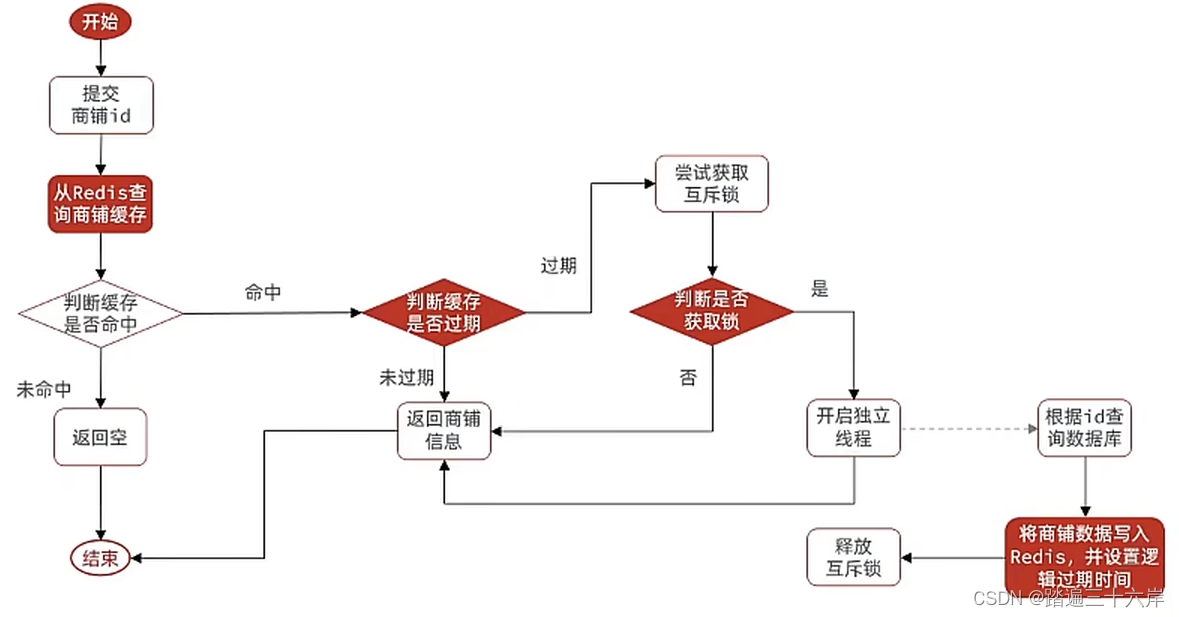
缓存技术(缓存穿透,缓存雪崩,缓存击穿)
大家好 , 我是苏麟 , 今天聊一聊缓存 . 这里需要一些Redis基础 (可以看相关文章等) 本文章资料来自于 : 黑马程序员 如果想要了解更详细的资料去黑马官网查看 前言:什么是缓存? 缓存,就是数据交换的 缓冲区 (称作Cache [ kʃ ] ),俗称的缓存就是缓冲区内的数据,是存贮数据的…...
实操教程 | 触发器实现 Apache DolphinScheduler 失败钉钉自动告警
作者 | sqlboy-yuzhenc 背景介绍 在实际应用中,我们经常需要将特定的任务通知给特定的人,虽然 Apache DolphinScheduler 在安全中心提供了告警组和告警实例,但是配置起来相对复杂,并且还需要在定时调度时指定告警组。通过这篇文…...

以“迅”防“汛”!5G视频快线筑牢防汛“安全堤”
近期,西安多地突发山洪泥石流灾害。防洪救灾刻不容缓,为进一步做好防汛工作,加强防洪调度监管,切实保障群众的生命财产安全,当地政府管理部门亟需拓展智能化技术,通过人防技防双保障提升防灾救灾应急处置能…...

jmeter 性能测试工具的使用(Web性能测试)
1、下载 该软件不用安装,直接解压打开即可使用。 2、使用 这里就在win下进行,图形界面较为方便 在目录apache-jmeter-2.13\bin 下可以见到一个jmeter.bat文件,双击此文件,即看到JMeter控制面板。主界面如下: 3、创…...
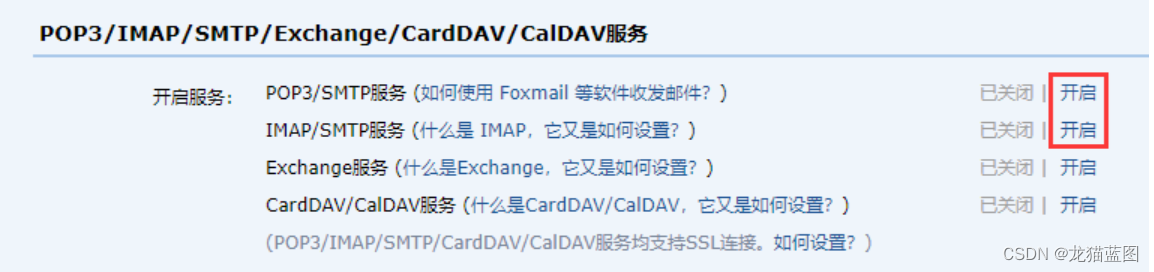
springboot整合第三方技术邮件系统
springboot整合第三方技术邮件系统,发邮件是java程序的基本操作,springboot整合javamail其实就是简化开发。不熟悉邮件的小伙伴可以先学习完javamail的基础操作,再来看这一部分内容才能感触到springboot整合javamail究竟简化了哪些操作。简化…...

Python入门学习——Day2-变量和数据类型
一、Python 变量 在Python中,变量用于保存数据,方便程序对数据的处理和操作。下面是关于Python变量的一些重要概念: 变量命名规则: 变量名由字母、数字和下划线组成。变量名可以以字母或下划线开头,但不能以数字开头…...
Graylog 更改显示的时区(Display timezone)
每个 Graylog 用户都可以配置他们的显示时区。 这会更改用于查看日志消息的时区,但不会更改日志消息的原始时区。 默认情况下,Graylog 显示 UTC 格式的所有时间戳(也就是 0:00)。就像是下面这样 非Admin账户要更改时区࿱…...

【网络安全防护】上海道宁与Bitdefender帮助您构建弹性网络并降低安全运营成本
在网络的世界中 风险变得更加常见与复杂 企业需要从网络安全转向网络弹性 复杂的网络攻击已非常普遍 在面临攻击时 企业如何保持业务连续性? Bitdefender GravityZone将 风险分析、安全加固、威胁预防 检测和响应功能相结合 帮助您构建弹性网络 并降低安全…...

文心一言 VS CHATGPT
由于近几天来,我的手机短信不断收到百度公司对于“文心一言”大模型的体验邀请(真是不胜其烦)!!所以我就抱着试试看的态度点开了文心一言的链接:文心一言 目前看来,有以下两点与chatgpt是有比较…...

2023-09-01力扣每日一题
链接: 2240. 买钢笔和铅笔的方案数 题意: 一共total元,两种笔分别cost1和cost2元,求能买的的笔的所有情况,不要求花光钱 解: 枚举其中一个数字就行 实际代码: #include<bits/stdc.h&g…...

【Python】从入门到上头— IO编程(8)
文章目录 一.IO编程是什么二.文件读写1.读取文件2.file-like Object二进制文件字符编码 3.写文件file对象的常用函数常见标识符 三.StringIO和BytesIO1.StringIO2.BytesIO 四.操作文件和目录五.序列化和反序列化1.pickle.dumps()2.pickle.loads()3.JSON 一.IO编程是什么 IO在计…...

R语言对综合社会调查GSS数据进行自举法bootstrap统计推断、假设检验、探索性数据分析可视化|数据分享...
全文链接:https://tecdat.cn/?p33514 综合社会调查(GSS)是由国家舆论研究中心开展的一项观察性研究。自 1972 年以来,GSS 一直通过收集当代社会的数据来监测社会学和态度趋势。其目的是解释态度、行为和属性的趋势和常量。从 197…...
LeetCode 刷题第四轮 Offer I + 类型题
目录 剑指 Offer 04. 二维数组中的查找 剑指 Offer 29. 顺时针打印矩阵 剑指 Offer 09. 用两个栈实现队列 剑指 Offer 30. 包含min函数的栈 剑指 Offer 10- I. 斐波那契数列 [类型:记忆优化 递归 / 动态规划] 剑指 Offer 10- II. 青蛙跳台阶问题 [类型&am…...
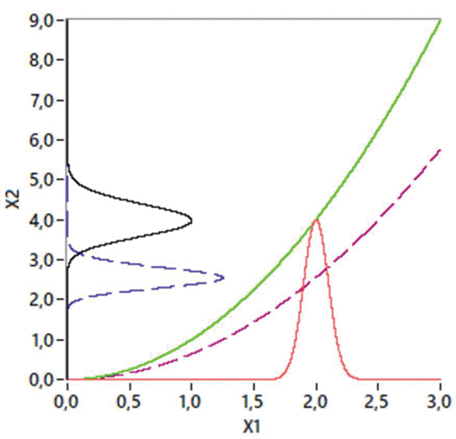
LabVIEW计算测量路径输出端随机变量的概率分布密度
LabVIEW计算测量路径输出端随机变量的概率分布密度 今天,开发算法和软件来解决计量综合的问题,即为特定问题寻找最佳测量算法。提出了算法支持,以便从计量上综合测量路径并确定所开发测量仪器的测量误差。测量路径由串联的几个块组成&#x…...
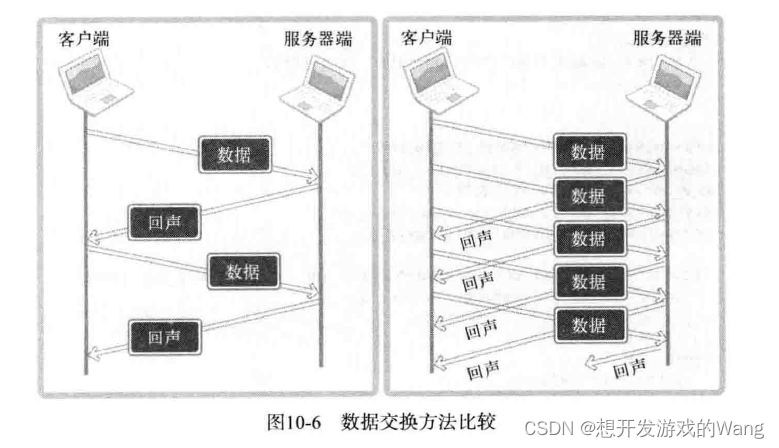
[C++ 网络协议] 多进程服务器端
具有代表性的并发服务器端实现模型和方法: 多进程服务器:通过创建多个进程提供服务。✔ 多路复用服务器:通过捆绑并统一管理I/O对象提供服务。 多线程服务器:通过生成与客户端等量的线程提供服务。 目录 1. 进程的概念及应用 1.…...
李宏毅 2022机器学习 HW2 strong baseline 上分路线
strong baseline上分路线 baseline增加concat_nframes (提升明显)增加batchnormalization 和 dropout增加hidden layer宽度至512 (提升明显) 提交文件命名规则为 prediction_{concat_nframes}[{n_hidden_layers}{dropout}_bn].c…...

伦敦银交易时间怎么选择?
伦敦银和伦敦金都是全球性的交易品种,一般的现货贵金属交易平台,都可以同时经营这两个品种,而且它们的交易时间是一致的,以香港市场的平台为例,基本上交易时间都会从北京周一的早上7点,延续到周六凌晨5点左…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...

【堆垛策略】设计方法
堆垛策略的设计是积木堆叠系统的核心,直接影响堆叠的稳定性、效率和容错能力。以下是分层次的堆垛策略设计方法,涵盖基础规则、优化算法和容错机制: 1. 基础堆垛规则 (1) 物理稳定性优先 重心原则: 大尺寸/重量积木在下…...

Matlab实现任意伪彩色图像可视化显示
Matlab实现任意伪彩色图像可视化显示 1、灰度原始图像2、RGB彩色原始图像 在科研研究中,如何展示好看的实验结果图像非常重要!!! 1、灰度原始图像 灰度图像每个像素点只有一个数值,代表该点的亮度(或…...

6.9-QT模拟计算器
源码: 头文件: widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QMouseEvent>QT_BEGIN_NAMESPACE namespace Ui { class Widget; } QT_END_NAMESPACEclass Widget : public QWidget {Q_OBJECTpublic:Widget(QWidget *parent nullptr);…...

WEB3全栈开发——面试专业技能点P4数据库
一、mysql2 原生驱动及其连接机制 概念介绍 mysql2 是 Node.js 环境中广泛使用的 MySQL 客户端库,基于 mysql 库改进而来,具有更好的性能、Promise 支持、流式查询、二进制数据处理能力等。 主要特点: 支持 Promise / async-await…...

【大模型】RankRAG:基于大模型的上下文排序与检索增强生成的统一框架
文章目录 A 论文出处B 背景B.1 背景介绍B.2 问题提出B.3 创新点 C 模型结构C.1 指令微调阶段C.2 排名与生成的总和指令微调阶段C.3 RankRAG推理:检索-重排-生成 D 实验设计E 个人总结 A 论文出处 论文题目:RankRAG:Unifying Context Ranking…...
:LSM Tree 概述)
从零手写Java版本的LSM Tree (一):LSM Tree 概述
🔥 推荐一个高质量的Java LSM Tree开源项目! https://github.com/brianxiadong/java-lsm-tree java-lsm-tree 是一个从零实现的Log-Structured Merge Tree,专为高并发写入场景设计。 核心亮点: ⚡ 极致性能:写入速度超…...

欢乐熊大话蓝牙知识17:多连接 BLE 怎么设计服务不会乱?分层思维来救场!
多连接 BLE 怎么设计服务不会乱?分层思维来救场! 作者按: 你是不是也遇到过 BLE 多连接时,调试现场像网吧“掉线风暴”? 温度传感器连上了,心率带丢了;一边 OTA 更新,一边通知卡壳。…...
