redis 应用 4: HyperLogLog
我们先思考一个常见的业务问题:如果你负责开发维护一个大型的网站,有一天老板找产品经理要网站每个网页每天的 UV 数据,然后让你来开发这个统计模块,你会如何实现?

如果统计 PV 那非常好办,给每个网页一个独立的 Redis 计数器就可以了,这个计数器的 key 后缀加上当天的日期。这样来一个请求,incrby 一次,最终就可以统计出所有的 PV 数据。
但是 UV 不一样,它要去重,同一个用户一天之内的多次访问请求只能计数一次。这就要求每一个网页请求都需要带上用户的 ID,无论是登陆用户还是未登陆用户都需要一个唯一 ID 来标识。
你也许已经想到了一个简单的方案,那就是为每一个页面一个独立的 set 集合来存储所有当天访问过此页面的用户 ID。当一个请求过来时,我们使用 sadd 将用户 ID 塞进去就可以了。通过 scard 可以取出这个集合的大小,这个数字就是这个页面的 UV 数据。没错,这是一个非常简单的方案。
但是,如果你的页面访问量非常大,比如一个爆款页面几千万的 UV,你需要一个很大的 set 集合来统计,这就非常浪费空间。如果这样的页面很多,那所需要的存储空间是惊人的。为这样一个去重功能就耗费这样多的存储空间,值得么?其实老板需要的数据又不需要太精确,105w 和 106w 这两个数字对于老板们来说并没有多大区别,So,有没有更好的解决方案呢?
这就是本节要引入的一个解决方案,Redis 提供了 HyperLogLog 数据结构就是用来解决这种统计问题的。HyperLogLog 提供不精确的去重计数方案,虽然不精确但是也不是非常不精确,标准误差是 0.81%,这样的精确度已经可以满足上面的 UV 统计需求了。
HyperLogLog 数据结构是 Redis 的高级数据结构,它非常有用,但是令人感到意外的是,使用过它的人非常少。
使用方法
HyperLogLog 提供了两个指令 pfadd 和 pfcount,根据字面意义很好理解,一个是增加计数,一个是获取计数。pfadd 用法和 set 集合的 sadd 是一样的,来一个用户 ID,就将用户 ID 塞进去就是。pfcount 和 scard 用法是一样的,直接获取计数值。
bash复制代码127.0.0.1:6379> pfadd codehole user1
(integer) 1
127.0.0.1:6379> pfcount codehole
(integer) 1
127.0.0.1:6379> pfadd codehole user2
(integer) 1
127.0.0.1:6379> pfcount codehole
(integer) 2
127.0.0.1:6379> pfadd codehole user3
(integer) 1
127.0.0.1:6379> pfcount codehole
(integer) 3
127.0.0.1:6379> pfadd codehole user4
(integer) 1
127.0.0.1:6379> pfcount codehole
(integer) 4
127.0.0.1:6379> pfadd codehole user5
(integer) 1
127.0.0.1:6379> pfcount codehole
(integer) 5
127.0.0.1:6379> pfadd codehole user6
(integer) 1
127.0.0.1:6379> pfcount codehole
(integer) 6
127.0.0.1:6379> pfadd codehole user7 user8 user9 user10
(integer) 1
127.0.0.1:6379> pfcount codehole
(integer) 10
简单试了一下,发现还蛮精确的,一个没多也一个没少。接下来我们使用脚本,往里面灌更多的数据,看看它是否还可以继续精确下去,如果不能精确,差距有多大。人生苦短,我用 Python!Python 脚本走起来!😄
py复制代码# coding: utf-8
import redis
client = redis.StrictRedis()
for i in range(1000):
client.pfadd("codehole", "user%d" % i)
total = client.pfcount("codehole")
if total != i+1:
print total, i+1
break
当然 Java 也不错,大同小异,下面是 Java 版本:
java复制代码public class PfTest {
public static void main(String[] args) {
Jedis jedis = new Jedis();
for (int i = 0; i < 1000; i++) {
jedis.pfadd("codehole", "user" + i);
long total = jedis.pfcount("codehole");
if (total != i + 1) {
System.out.printf("%d %d\n", total, i + 1);
break;
}
}
jedis.close();
}
}
我们来看下输出:
markdown复制代码> python pftest.py
99 100
当我们加入第 100 个元素时,结果开始出现了不一致。接下来我们将数据增加到 10w 个,看看总量差距有多大。
css复制代码# coding: utf-8
import redis
client = redis.StrictRedis()
for i in range(100000):
client.pfadd("codehole", "user%d" % i)
print 100000, client.pfcount("codehole")
Java 版:
java复制代码public class JedisTest {
public static void main(String[] args) {
Jedis jedis = new Jedis();
for (int i = 0; i < 100000; i++) {
jedis.pfadd("codehole", "user" + i);
}
long total = jedis.pfcount("codehole");
System.out.printf("%d %d\n", 100000, total);
jedis.close();
}
}
跑了约半分钟,我们看输出:
markdown复制代码> python pftest.py
100000 99723
差了 277 个,按百分比是 0.277%,对于上面的 UV 统计需求来说,误差率也不算高。然后我们把上面的脚本再跑一边,也就相当于将数据重复加入一边,查看输出,可以发现,pfcount 的结果没有任何改变,还是 99723,说明它确实具备去重功能。
pfadd 这个 pf 是什么意思?
它是 HyperLogLog 这个数据结构的发明人 Philippe Flajolet 的首字母缩写,老师觉得他发型很酷,看起来是个佛系教授。

pfmerge 适合什么场合用?
HyperLogLog 除了上面的 pfadd 和 pfcount 之外,还提供了第三个指令 pfmerge,用于将多个 pf 计数值累加在一起形成一个新的 pf 值。
比如在网站中我们有两个内容差不多的页面,运营说需要这两个页面的数据进行合并。其中页面的 UV 访问量也需要合并,那这个时候 pfmerge 就可以派上用场了。
注意事项
HyperLogLog 这个数据结构不是免费的,不是说使用这个数据结构要花钱,它需要占据一定 12k 的存储空间,所以它不适合统计单个用户相关的数据。如果你的用户上亿,可以算算,这个空间成本是非常惊人的。但是相比 set 存储方案,HyperLogLog 所使用的空间那真是可以使用千斤对比四两来形容了。
不过你也不必过于担心,因为 Redis 对 HyperLogLog 的存储进行了优化,在计数比较小时,它的存储空间采用稀疏矩阵存储,空间占用很小,仅仅在计数慢慢变大,稀疏矩阵占用空间渐渐超过了阈值时才会一次性转变成稠密矩阵,才会占用 12k 的空间。
HyperLogLog 实现原理
HyperLogLog 的使用非常简单,但是实现原理比较复杂,如果读者没有特别的兴趣,下面的内容暂时可以跳过不看。
为了方便理解 HyperLogLog 的内部实现原理,我画了下面这张图

这张图的意思是,给定一系列的随机整数,我们记录下低位连续零位的最大长度 k,通过这个 k 值可以估算出随机数的数量。 首先不问为什么,我们编写代码做一个实验,观察一下随机整数的数量和 k 值的关系。
py复制代码import math
import random
# 算低位零的个数
def low_zeros(value):
for i in xrange(1, 32):
if value >> i << i != value:
break
return i - 1
# 通过随机数记录最大的低位零的个数
class BitKeeper(object):
def __init__(self):
self.maxbits = 0
def random(self):
value = random.randint(0, 2**32-1)
bits = low_zeros(value)
if bits > self.maxbits:
self.maxbits = bits
class Experiment(object):
def __init__(self, n):
self.n = n
self.keeper = BitKeeper()
def do(self):
for i in range(self.n):
self.keeper.random()
def debug(self):
print self.n, '%.2f' % math.log(self.n, 2), self.keeper.maxbits
for i in range(1000, 100000, 100):
exp = Experiment(i)
exp.do()
exp.debug()
Java 版:
java复制代码public class PfTest {
static class BitKeeper {
private int maxbits;
public void random() {
long value = ThreadLocalRandom.current().nextLong(2L << 32);
int bits = lowZeros(value);
if (bits > this.maxbits) {
this.maxbits = bits;
}
}
private int lowZeros(long value) {
int i = 1;
for (; i < 32; i++) {
if (value >> i << i != value) {
break;
}
}
return i - 1;
}
}
static class Experiment {
private int n;
private BitKeeper keeper;
public Experiment(int n) {
this.n = n;
this.keeper = new BitKeeper();
}
public void work() {
for (int i = 0; i < n; i++) {
this.keeper.random();
}
}
public void debug() {
System.out.printf("%d %.2f %d\n", this.n, Math.log(this.n) / Math.log(2), this.keeper.maxbits);
}
}
public static void main(String[] args) {
for (int i = 1000; i < 100000; i += 100) {
Experiment exp = new Experiment(i);
exp.work();
exp.debug();
}
}
}
运行观察输出:
复制代码36400 15.15 13
36500 15.16 16
36600 15.16 13
36700 15.16 14
36800 15.17 15
36900 15.17 18
37000 15.18 16
37100 15.18 15
37200 15.18 13
37300 15.19 14
37400 15.19 16
37500 15.19 14
37600 15.20 15
通过这实验可以发现 K 和 N 的对数之间存在显著的线性相关性:
ini
复制代码N=2^K # 约等于
如果 N 介于 2^K 和 2^(K+1) 之间,用这种方式估计的值都等于 2^K,这明显是不合理的。这里可以采用多个 BitKeeper,然后进行加权估计,就可以得到一个比较准确的值。
py复制代码import math
import random
def low_zeros(value):
for i in xrange(1, 32):
if value >> i << i != value:
break
return i - 1
class BitKeeper(object):
def __init__(self):
self.maxbits = 0
def random(self, m):
bits = low_zeros(m)
if bits > self.maxbits:
self.maxbits = bits
class Experiment(object):
def __init__(self, n, k=1024):
self.n = n
self.k = k
self.keepers = [BitKeeper() for i in range(k)]
def do(self):
for i in range(self.n):
m = random.randint(0, 1<<32-1)
# 确保同一个整数被分配到同一个桶里面,摘取高位后取模
keeper = self.keepers[((m & 0xfff0000) >> 16) % len(self.keepers)]
keeper.random(m)
def estimate(self):
sumbits_inverse = 0 # 零位数倒数
for keeper in self.keepers:
sumbits_inverse += 1.0/float(keeper.maxbits)
avgbits = float(self.k)/sumbits_inverse # 平均零位数
return 2**avgbits * self.k # 根据桶的数量对估计值进行放大
for i in range(100000, 1000000, 100000):
exp = Experiment(i)
exp.do()
est = exp.estimate()
print i, '%.2f' % est, '%.2f' % (abs(est-i) / i)
下面是 Java 版:
java复制代码public class PfTest {
static class BitKeeper {
private int maxbits;
public void random(long value) {
int bits = lowZeros(value);
if (bits > this.maxbits) {
this.maxbits = bits;
}
}
private int lowZeros(long value) {
int i = 1;
for (; i < 32; i++) {
if (value >> i << i != value) {
break;
}
}
return i - 1;
}
}
static class Experiment {
private int n;
private int k;
private BitKeeper[] keepers;
public Experiment(int n) {
this(n, 1024);
}
public Experiment(int n, int k) {
this.n = n;
this.k = k;
this.keepers = new BitKeeper[k];
for (int i = 0; i < k; i++) {
this.keepers[i] = new BitKeeper();
}
}
public void work() {
for (int i = 0; i < this.n; i++) {
long m = ThreadLocalRandom.current().nextLong(1L << 32);
BitKeeper keeper = keepers[(int) (((m & 0xfff0000) >> 16) % keepers.length)];
keeper.random(m);
}
}
public double estimate() {
double sumbitsInverse = 0.0;
for (BitKeeper keeper : keepers) {
sumbitsInverse += 1.0 / (float) keeper.maxbits;
}
double avgBits = (float) keepers.length / sumbitsInverse;
return Math.pow(2, avgBits) * this.k;
}
}
public static void main(String[] args) {
for (int i = 100000; i < 1000000; i += 100000) {
Experiment exp = new Experiment(i);
exp.work();
double est = exp.estimate();
System.out.printf("%d %.2f %.2f\n", i, est, Math.abs(est - i) / i);
}
}
}
代码中分了 1024 个桶,计算平均数使用了调和平均 (倒数的平均)。普通的平均法可能因为个别离群值对平均结果产生较大的影响,调和平均可以有效平滑离群值的影响。

观察脚本的输出,误差率控制在百分比个位数:
复制代码100000 97287.38 0.03
200000 189369.02 0.05
300000 287770.04 0.04
400000 401233.52 0.00
500000 491704.97 0.02
600000 604233.92 0.01
700000 721127.67 0.03
800000 832308.12 0.04
900000 870954.86 0.03
1000000 1075497.64 0.08
真实的 HyperLogLog 要比上面的示例代码更加复杂一些,也更加精确一些。上面的这个算法在随机次数很少的情况下会出现除零错误,因为 maxbits=0 是不可以求倒数的。
pf 的内存占用为什么是 12k?
我们在上面的算法中使用了 1024 个桶进行独立计数,不过在 Redis 的 HyperLogLog 实现中用到的是 16384 个桶,也就是 2^14,每个桶的 maxbits 需要 6 个 bits 来存储,最大可以表示 maxbits=63,于是总共占用内存就是2^14 * 6 / 8 = 12k字节。
本文由 mdnice 多平台发布
相关文章:

redis 应用 4: HyperLogLog
我们先思考一个常见的业务问题:如果你负责开发维护一个大型的网站,有一天老板找产品经理要网站每个网页每天的 UV 数据,然后让你来开发这个统计模块,你会如何实现? img 如果统计 PV 那非常好办,给每个网页一…...

进程的挂起状态
进程的挂起状态详解 当我们谈论操作系统和进程管理时,我们经常听到进程的各种状态,如“就绪”、“运行”和“阻塞”。但其中一个不那么常被提及,但同样重要的状态是“挂起”状态。本文将深入探讨挂起状态,以及为什么和在何时进程…...
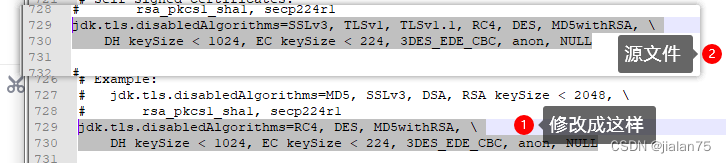
idea 链接mysql连不上
打开文件 C:\Program Files\JetBrains\IntelliJ IDEA 2023.2.1\jbr\conf\security\java.security修改内容 搜索:jdk.tls.disabledAlgorithms 修改 链接地址 在链接后面添加 ?useSSLfalse jdbc:mysql://127.0.0.1:3306/db_admin3?useSSLfalse...

Ubuntu 启动出现grub rescue
一,原因 原因:出现 “grub rescue” 错误通常表示您的计算机无法正常引导到操作系统,而是进入了 GRUB(Grand Unified Bootloader)紧急模式。这可能是由于引导加载程序配置错误、硬盘驱动器损坏或其他引导问题引起…...

go中runtime包里面的mutex是什么?runtime.mutex解析
其实在看go源码的时候,发现除了sync包里有个mutex以外,runtime包里也有一个mutex,这个mutex在runtime很多地方都在用。 这个runtime包里面的mutex的结构如下: 目录: /runtime/runtime2.go 代码: type mutex struct …...

VScode 调试python程序,debug状态闪断问题的解决方法
0. Few words 之前一直在VSCode中debug C和Python的程序没出过闪断的问题,但是最近在另一台电脑上debug,同样的方法,设置launch.json和CMakeList加debug状态等等操作,如我另一篇blog写的一样,可以点这里查看。 但是&a…...

飞桨中的李宏毅课程中的第一个项目——PM2.5的预测
所谓的激活函数,就是李宏毅老师讲到的sigmoid函数 和 hard sigmoid函数 ,ReLU函数那些 现在一点点慢慢探索,会成为日后想都做不到的经历,当你啥也不会的时候,才是慢慢享受探索的过程。 有一说一,用chatGP…...
Qt---对话框 事件处理 如何发布自己写的软件
目录 一、对话框 1.1 消息对话框(QMessageBox) 1> 消息对话框提供了一个模态的对话框,用来提示用户信息,或者询问用户问题并得到回答 2> 基于属性版本的API 3> 基于静态成员函数版本 4> 对话框案例 1、ui界面 …...
【C++】C++ 引用详解 ⑩ ( 常量引用案例 )
文章目录 一、常量引用语法1、语法简介2、常引用语法示例 二、常量引用语法1、int 类型常量引用示例2、结构体类型常量引用示例 在 C 语言中 , 常量引用 是 引用类型 的一种 ; 借助 常量引用 , 可以将一个变量引用 作为实参 传递给一个函数形参 , 同时保证该值不会在函数内部被…...
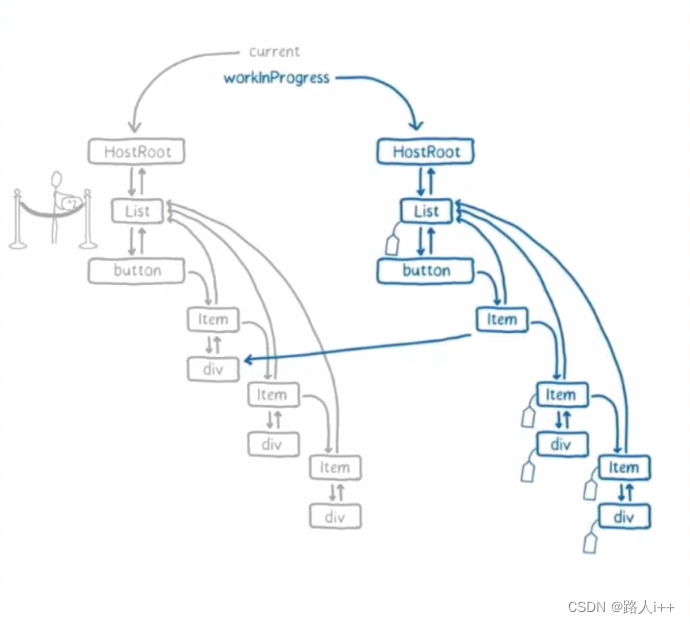
React原理 - React Reconciliation-下
目录 Fiber Reconciler 【react v16.13.1】 React Fiber需要解决的问题 React Fiber的数据结构 时间分片 Fiber Reconciler 的调度 双缓冲 池概念 小节 练习 Fiber Reconciler 【react v16.13.1】 Fiber 协调 优化了栈协调的事务性弊端引起的卡顿 React Fiber需要解决…...

YOLOv8超参数调优教程! 使用Ray Tune进行高效的超参数调优!
原创文章为博主个人所有,未经授权不得转载、摘编、倒卖、洗稿或利用其它方式使用上述作品。违反上述声明者,本站将追求其相关法律责任。 这篇博文带大家玩点新的东西,也是一直以来困扰大家最大的问题—超参数调优! 之前的 YOLOv5 我使用遗传算法做过很多次调优,实验一跑就…...
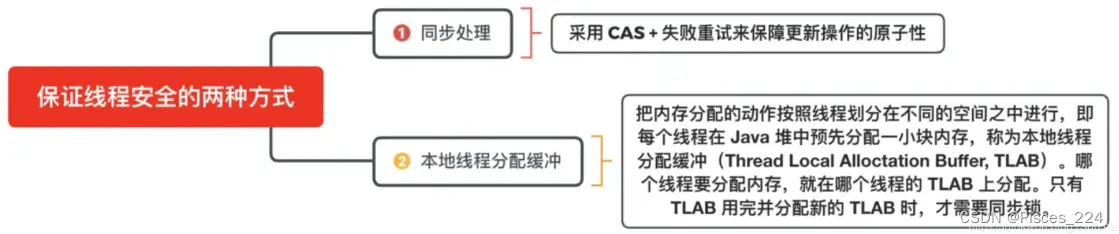
JVM运行时数据区
文章目录 JVM内存结构图1、运行时数据区域JDK 1.7JDK 1.81. 线程栈(虚拟机栈)2. 本地方法栈3. 程序计数器4. 方法区(元空间)5. 堆6、运行时常量池(Runtime Constant Pool)7、直接内存(Direct Me…...

第七章,相似矩阵及其应用,3-二次型、合同矩阵与合同变换
第七章,相似矩阵及其应用,3-二次型、合同矩阵与合同变换 二次型相关概念二次型二次型的标准形和规范形表示形式 合同矩阵与合同变换定义 合同合同矩阵的性质等价、相似、合同三种关系的对比等价相似合同 玩转线性代数(38)二次型概念、合同矩阵与合同变换…...

css学习7(盒子模型)
1、盒子模型图: Margin(外边距) - 清除边框外的区域,外边距是透明的。Border(边框) - 围绕在内边距和内容外的边框。Padding(内边距) - 清除内容周围的区域,内边距是透明的。Content(内容) - 盒子的内容,显示文本和图像。 <!DO…...
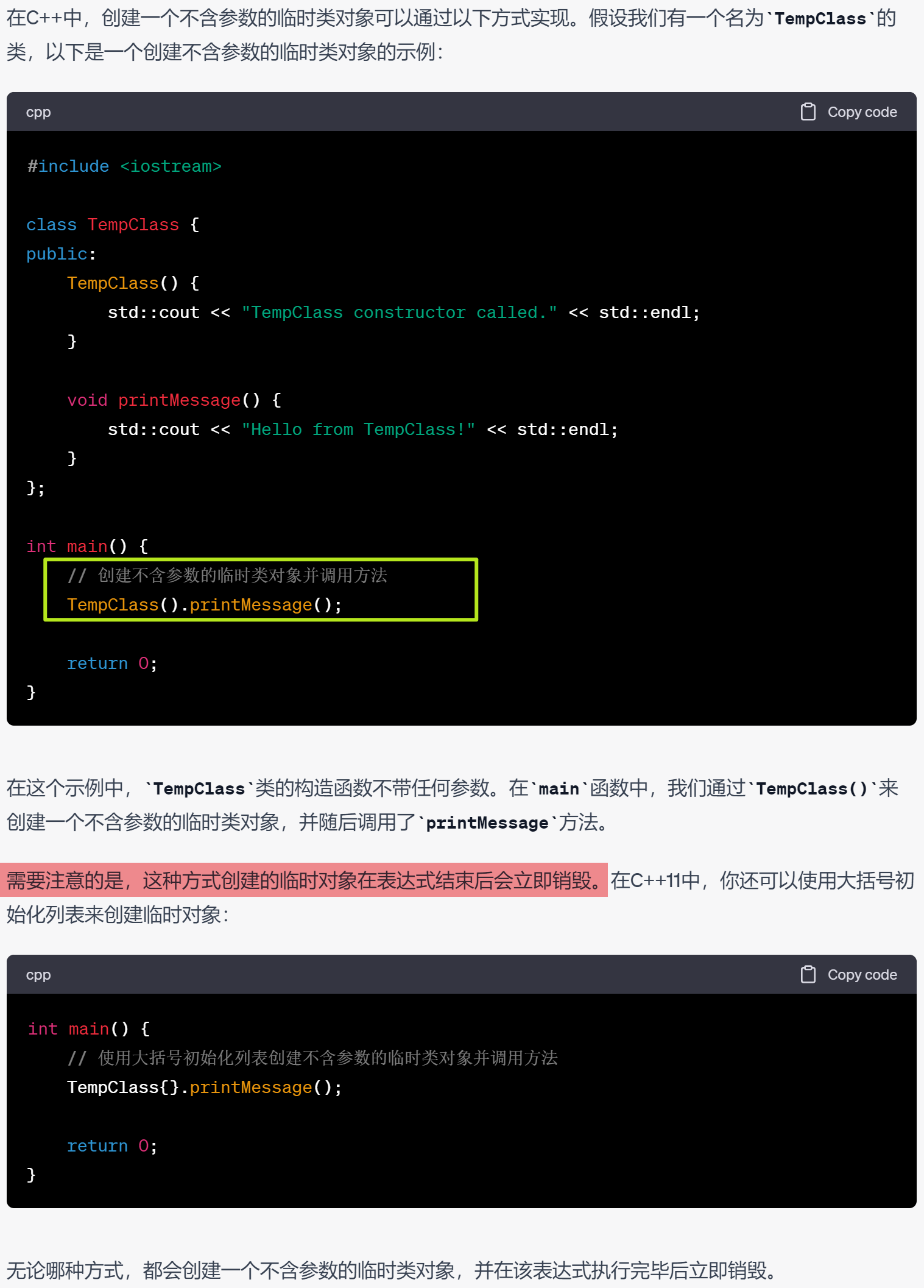
C++笔记之临时变量与临时对象与匿名对象
C笔记之临时变量与临时对象与匿名对象 code review! 文章目录 C笔记之临时变量与临时对象与匿名对象1.C中的临时变量指的是什么?2.C中的临时对象指的是什么?3.C中临时对象的作用是什么?什么时候要用到临时对象?4.给我列举具体的例子说明临…...
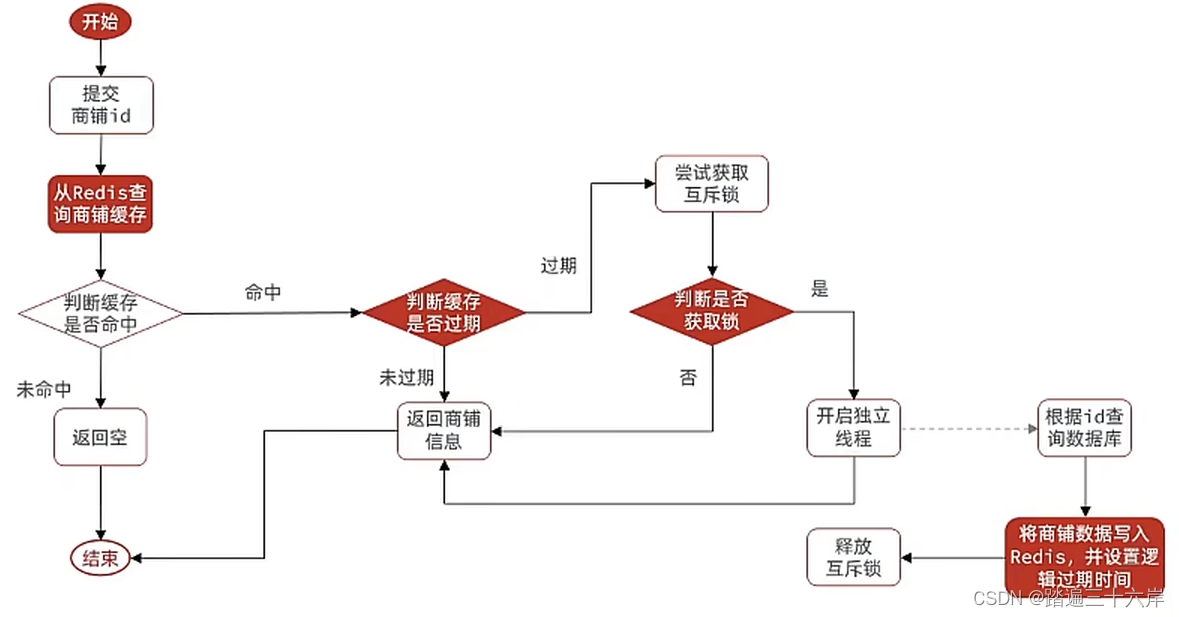
缓存技术(缓存穿透,缓存雪崩,缓存击穿)
大家好 , 我是苏麟 , 今天聊一聊缓存 . 这里需要一些Redis基础 (可以看相关文章等) 本文章资料来自于 : 黑马程序员 如果想要了解更详细的资料去黑马官网查看 前言:什么是缓存? 缓存,就是数据交换的 缓冲区 (称作Cache [ kʃ ] ),俗称的缓存就是缓冲区内的数据,是存贮数据的…...
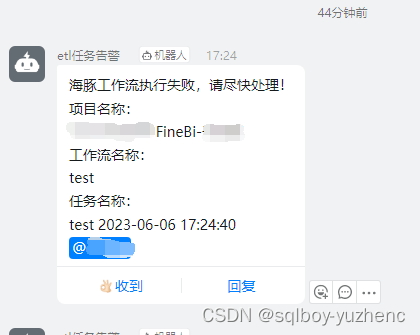
实操教程 | 触发器实现 Apache DolphinScheduler 失败钉钉自动告警
作者 | sqlboy-yuzhenc 背景介绍 在实际应用中,我们经常需要将特定的任务通知给特定的人,虽然 Apache DolphinScheduler 在安全中心提供了告警组和告警实例,但是配置起来相对复杂,并且还需要在定时调度时指定告警组。通过这篇文…...

以“迅”防“汛”!5G视频快线筑牢防汛“安全堤”
近期,西安多地突发山洪泥石流灾害。防洪救灾刻不容缓,为进一步做好防汛工作,加强防洪调度监管,切实保障群众的生命财产安全,当地政府管理部门亟需拓展智能化技术,通过人防技防双保障提升防灾救灾应急处置能…...

jmeter 性能测试工具的使用(Web性能测试)
1、下载 该软件不用安装,直接解压打开即可使用。 2、使用 这里就在win下进行,图形界面较为方便 在目录apache-jmeter-2.13\bin 下可以见到一个jmeter.bat文件,双击此文件,即看到JMeter控制面板。主界面如下: 3、创…...
springboot整合第三方技术邮件系统
springboot整合第三方技术邮件系统,发邮件是java程序的基本操作,springboot整合javamail其实就是简化开发。不熟悉邮件的小伙伴可以先学习完javamail的基础操作,再来看这一部分内容才能感触到springboot整合javamail究竟简化了哪些操作。简化…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...
