判断聚类 n_clusters
目录
基本原理
代码实现:
肘部法则(Elbow Method):
轮廓系数(Silhouette Coefficient)
Gap Statistic(间隙统计量):
Calinski-Harabasz Index(Calinski-Harabasz指数):
基本原理
这些方法(肘部法则、轮廓系数、Gap Statistic、Calinski-Harabasz Index)都是用于确定聚类算法中的 n_clusters(簇的数量)参数,但它们之间存在一些区别。下面是它们的主要特点以及适用情况的总结:
-
肘部法则(Elbow Method):
- 特点:通过绘制聚类结果的损失函数值与
n_clusters的关系图,找到“肘部”处的拐点作为最佳n_clusters。 - 适用情况:当数据集的聚类结构明显时,该方法通常有效。但是,对于数据集没有明显的肘部的情况,或者肘部并不明显时,该方法可能无法提供确定的最佳
n_clusters。
- 特点:通过绘制聚类结果的损失函数值与
-
轮廓系数(Silhouette Coefficient):
- 特点:计算每个样本的轮廓系数(介于-1和1之间),并计算出所有样本的平均轮廓系数。最大化平均轮廓系数可以确定最佳的
n_clusters。 - 适用情况:适用于各种类型的数据集,尤其是数据分布相对均匀且没有明显的几何形状的聚类结构。需要注意的是,轮廓系数的计算复杂度较高,对于大型数据集可能会有一定的性能开销。
- 特点:计算每个样本的轮廓系数(介于-1和1之间),并计算出所有样本的平均轮廓系数。最大化平均轮廓系数可以确定最佳的
-
Gap Statistic(间隙统计量):
- 特点:通过比较聚类结果与随机数据模拟结果的区别,使用统计学原理来选择最佳
n_clusters。Gap Statistic 值越大,表示聚类效果越好。 - 适用情况:适合于具有明显聚类结构的数据集,对于不同密度、大小和形状的聚类表现较好。需要注意的是,该方法对数据集的假设要求较高,在某些情况下可能会得到不准确的结果。
- 特点:通过比较聚类结果与随机数据模拟结果的区别,使用统计学原理来选择最佳
-
Calinski-Harabasz Index(Calinski-Harabasz指数):
- 特点:通过计算聚类之间的离散度与聚类内部的紧密度之比,确定最佳的
n_clusters。Calinski-Harabasz 指数值越大,表示聚类效果越好。 - 适用情况:适合于具有清晰、凸形状的聚类结构的数据集。对噪声和异常值比较敏感,处理非凸形状的聚类时可能出现一些偏差。
- 特点:通过计算聚类之间的离散度与聚类内部的紧密度之比,确定最佳的
在选择适当的方法时,应综合考虑以下因素:
- 数据特征:数据集的聚类结构、形状、噪声以及是否具有明显的几何形态等特征。
- 算法要求:不同的方法可能对数据集的假设和计算复杂度有不同的要求。
- 领域知识:对数据集具有领域知识,可以帮助理解数据的特点,并选择适合的评估指标和方法。
代码实现:
肘部法则(Elbow Method):
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
# 肘部法则(Elbow Method):绘制不同 n_clusters 下的聚类误差平方和(SSE)曲线。
# 观察 SSE 曲线的形状,找到一个"肘部弯曲点",
# 即在该点后,SSE 的下降速度变得缓慢。
# "肘部弯曲点"对应的 n_clusters 值就是一个合适的选择。
#
# 例如,在上述代码示例中,使用 plt.plot(k_range, sse, 'bx-') 绘制了 SSE 曲线。观察曲线,如果在某个 n_clusters 值处出现明显弯曲,且在该点之后 SSE 的下降速度变得缓慢,那么该 n_clusters 值可以被认为是一个合适的选择。# 加载Iris数据集
iris = load_iris()# 构造K-Means聚类模型
model = KMeans()# 肘部法则选择n_clusters
sse = []
k_range = range(2, 10) # 需要尝试的n_clusters范围
for k in k_range:model.set_params(n_clusters=k)model.fit(iris.data)sse.append(model.inertia_)plt.plot(k_range, sse, 'bx-')
plt.xlabel('Number of Clusters (k)')
plt.ylabel('SSE')
plt.title('The Elbow Method')
plt.show()# 轮廓系数选择n_clusters
silhouette_scores = []
for k in k_range:model.set_params(n_clusters=k)labels = model.fit_predict(iris.data)score = silhouette_score(iris.data, labels)silhouette_scores.append(score)plt.plot(k_range, silhouette_scores, 'bx-')
plt.xlabel('Number of Clusters (k)')
plt.ylabel('Silhouette Coefficient')
plt.title('Silhouette Score')
plt.show()轮廓系数(Silhouette Coefficient)
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score# 加载Iris数据集
iris = load_iris()# 构造K-Means聚类模型
model = KMeans()k_range = range(2, 10) # 需要尝试的n_clusters范围
silhouette_scores = []
for k in k_range:model.set_params(n_clusters=k)labels = model.fit_predict(iris.data)score = silhouette_score(iris.data, labels)silhouette_scores.append(score)plt.plot(k_range, silhouette_scores, 'bx-')
plt.xlabel('Number of Clusters (k)')
plt.ylabel('Silhouette Coefficient')
plt.title('Silhouette Score')
plt.show()
-
Gap Statistic(间隙统计量):
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.cluster import KMeans
from sklearn.metrics import pairwise_distances
from sklearn.metrics import silhouette_score
# 选择 Gap Statistic 最大的 n_clusters 值。
# 加载Iris数据集
iris = load_iris()# 构造K-Means聚类模型
model = KMeans()k_range = range(2, 10) # 需要尝试的n_clusters范围
gap_scores = []
for k in k_range:model.set_params(n_clusters=k)labels = model.fit_predict(iris.data)dist_matrix = pairwise_distances(iris.data)gap = np.mean(np.log(np.mean(np.min(dist_matrix[:, labels], axis=1))))gap_scores.append(gap)plt.plot(k_range, gap_scores, 'bx-')
plt.xlabel('Number of Clusters (k)')
plt.ylabel('Gap Statistic')
plt.title('Gap Statistic')
plt.show()
-
Calinski-Harabasz Index(Calinski-Harabasz指数):
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.cluster import KMeans
from sklearn.metrics import calinski_harabasz_score
# 选择具有最大 Calinski-Harabasz 指数的 n_clusters 值。
# 加载Iris数据集
iris = load_iris()# 构造K-Means聚类模型
model = KMeans()k_range = range(2, 10) # 需要尝试的n_clusters范围
calinski_scores = []
for k in k_range:model.set_params(n_clusters=k)labels = model.fit_predict(iris.data)score = calinski_harabasz_score(iris.data, labels)calinski_scores.append(score)plt.plot(k_range, calinski_scores, 'bx-')
plt.xlabel('Number of Clusters (k)')
plt.ylabel('Calinski-Harabasz Index')
plt.title('Calinski-Harabasz Index')
plt.show()
相关文章:

判断聚类 n_clusters
目录 基本原理 代码实现: 肘部法则(Elbow Method): 轮廓系数(Silhouette Coefficient) Gap Statistic(间隙统计量): Calinski-Harabasz Index(Calinski-…...

基于深度学习的网络异常检测方法研究
摘要: 本文提出了一种基于深度学习的网络异常检测方法,旨在有效地识别网络中潜在的异常行为。通过利用深度学习算法,结合大规模网络流量数据的训练,我们实现了对复杂网络环境下的异常行为的准确检测与分类。实验结果表明…...
SSM 基于注解的整合实现
一、pom.xml <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http://maven.apache.org/POM/4.0.0 http://maven.apache.org/maven-v4_0_0.xsd"><modelV…...

工具类APP如何解决黏性差、停留短、打开率低等痛点?
工具产品除了需要把自己的功能做到极致之外,其实需要借助一些情感手段、增设一些游戏机制、输出高质量内容、搭建社区组建用户关系链等方式,来提高产品的用户黏性,衍生产品的价值链。 工具类产品由于进入门槛低,竞争尤为激烈&…...

使用Java MVC开发高效、可扩展的Web应用
在当今的Web开发领域,高效和可扩展性是我们追求的目标。Java作为一种强大且广泛使用的编程语言,提供了丰富的工具和框架来支持Web应用的开发。其中,MVC模式是一种被广泛采用的架构模式,它能够有效地组织和管理代码,使得…...

wandb安装方法及本地部署教程
文章目录 1 wandb介绍2 wandb安装2.1 注册wandb账号2.2 创建项目并获得密钥2.3 安装wandb并登录 3 wandb本地部署3.1 设置wandb运行模式3.2 云端查看运行数据 4 总结 1 wandb介绍 Wandb(Weights & Biases)是一个用于跟踪、可视化和协作机器学习实验…...
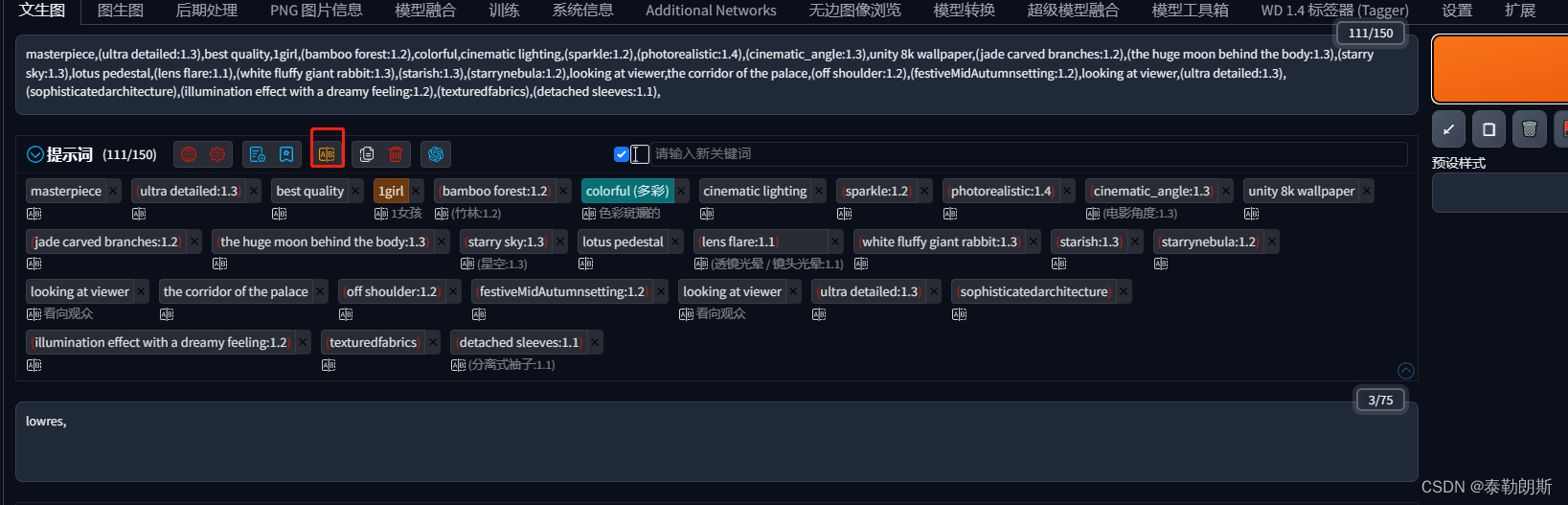
stable diffusion实践操作-提示词插件安装与使用
本文专门开一节写提示词相关的内容,在看之前,可以同步关注: stable diffusion实践操作 正文 1、提示词插件安装 1.1、 安装 1.2 加载【应用更改并重载前端】 1.3 界面展示 1.3.-4 使用 里面有个收藏列表,可以收藏以前的所有提示…...

【SpringBoot】详细介绍SpringBoot中的bean
在Spring Boot中,Bean是由Spring容器实例化、管理和维护的对象。Bean是Spring框架的核心概念之一,它代表了应用程序中的组件或对象。 以下是有关Spring Boot中Bean的详细介绍: 1. 定义:Bean是在Spring容器中被实例化、管理和维护…...

【Nuxt实战】在Nuxt3项目中如何按需引入Element-plus
步骤一:安装 Element Plus 和图标库 首先,使用以下命令安装 Element Plus 和它的图标库: npm install element-plus --save npm install element-plus/icons-vue步骤二:安装 Nuxt Element Plus 模块 安装 Nuxt Element Plus 模…...

专业制造一体化ERP系统,专注于制造工厂生产管理信息化,可定制-亿发
制造业是国民经济的支柱产业,对于经济发展和竞争力至关重要。在数字化和智能化趋势的推动下,制造业正处于升级的关键时期。而ERP系统,即企业资源计划系统,能够将企业的各个业务环节整合起来,实现资源的有效管理和信息的…...

Linux工具
一、yum yum可以看作一个客户端(应用商店)、应用程序,它如何知道去哪里下载软件? yum也是一个指令/程序,可以找到它的安装路径。 在list中可以看到yum能安装的所有软件,通过管道找到想要的,yum …...

Java项目-苍穹外卖-Day07-redis缓存应用-SpringCache/购物车功能
文章目录 前言缓存菜品问题分析和实现思路缓存菜品数据清理缓存数据功能测试 SpringCache介绍入门案例 缓存套餐购物车功能添加购物车需求分析和产品原型测试 查看购物车清空购物车 前言 本章节主要是进行用户端的购物车功能开发 和redis作为mysql缓存的应用以及SpringCache的…...

零知识证明(zk-SNARK)(一)
全称为 Zero-Knowledge Succinct Non-Interactive Argument of Knowledge,简洁非交互式零知识证明,简洁性使得运行该协议时,即便statement非常大,它的proof大小也仅有几百个bytes,并且验证一个proof的时间可以达到毫秒…...

linux中打印数据的行缓冲模式
1. 回车换行符在Window下和在Linux下的区别: 在Window下:回车换行符为\r\n 在Linux下:回车换行符为\n \n为换行符,换行相当于光标跳转到下一行的这个位置 \r为回车符,回车相当于光标跳转到当前行的最左边的位置 所以…...

香橙派OrangePi zero H2+ 驱动移远4G/5G模块
目录 1 安装系统和内核文件: 1.1 下载镜像 1.2 内核头安装 1.2.1 下载内核 1.2.2 将内核头文件导入开发板中 1.2.3 安装内核头 2 安装依赖工具: 2.1 Installing Required Host Utilities 3 驱动步骤: 3.1 下载模块驱动文件…...

自动驾驶——【规划】记忆泊车特殊学习路径拟合
1.Back ground 如上图,SLAM学习路线Start到End路径,其中曲线SDAB为D档位学习路径,曲线BC为R学习路径,曲线AE为前进档D档学习路径。 为了使其使用记忆泊车时,其驾驶员体验感好,需去除R档倒车部分轨迹&#x…...
)
【跟小嘉学 Rust 编程】十六、无畏并发(Fearless Concurrency)
系列文章目录 【跟小嘉学 Rust 编程】一、Rust 编程基础 【跟小嘉学 Rust 编程】二、Rust 包管理工具使用 【跟小嘉学 Rust 编程】三、Rust 的基本程序概念 【跟小嘉学 Rust 编程】四、理解 Rust 的所有权概念 【跟小嘉学 Rust 编程】五、使用结构体关联结构化数据 【跟小嘉学…...
)
Android 进阶——图形显示系统之VSync和 Choreographer的创建详解(一)
引言 前一篇文章Android 进阶——图形显示系统之底层图像显示原理小结(一)介绍了关于Android 图形显示系统的基础理论,相信你对于Android的图形显示系统中图形界面渲染刷新机制有了更深的了解,接下来进一步讲解VSync和Choreography的联系和作用。 一、VSync 信号的产生概…...
SQL Server开启变更数据捕获(CDC)
一、CDC简介 变更数据捕获(Change Data Capture ,简称 CDC):记录 SQL Server 表的插入、更新和删除操作。开启cdc的源表在插入、更新和删除操作时会插入数据到日志表中。cdc通过捕获进程将变更数据捕获到变更表中,通过…...

八、性能测试
八、性能测试 8.1 性能测试代码 #include"ConcurrentAlloc.h"// ntimes 一轮申请和释放内存的次数 // rounds 轮次 void BenchmarkMalloc(size_t ntimes, size_t nworks, size_t rounds) {std::vector<std::thread> vthread(nworks);std::atomic<size_t&g…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

无需布线的革命:电力载波技术赋能楼宇自控系统-亚川科技
无需布线的革命:电力载波技术赋能楼宇自控系统 在楼宇自动化领域,传统控制系统依赖复杂的专用通信线路,不仅施工成本高昂,后期维护和扩展也极为不便。电力载波技术(PLC)的突破性应用,彻底改变了…...

Axure Rp 11 安装、汉化、授权
Axure Rp 11 安装、汉化、授权 1、前言2、汉化2.1、汉化文件下载2.2、windows汉化流程2.3、 macOs汉化流程 3、授权 1、前言 Axure Rp 11官方下载链接:https://www.axure.com/downloadthanks 2、汉化 2.1、汉化文件下载 链接: https://pan.baidu.com/s/18Clf…...

OpenHarmony标准系统-HDF框架之I2C驱动开发
文章目录 引言I2C基础知识概念和特性协议,四种信号组合 I2C调试手段硬件软件 HDF框架下的I2C设备驱动案例描述驱动Dispatch驱动读写 总结 引言 I2C基础知识 概念和特性 集成电路总线,由串网12C(1C、12C、Inter-Integrated Circuit BUS)行数据线SDA和串…...
