leetcode做题笔记119. 杨辉三角 II
给定一个非负索引 rowIndex,返回「杨辉三角」的第 rowIndex 行。
在「杨辉三角」中,每个数是它左上方和右上方的数的和。
思路一:模拟题意
int* getRow(int rowIndex, int* returnSize){int* ret = malloc(sizeof(int)*(rowIndex+1));ret[0] = 1;*returnSize = rowIndex+1;if(rowIndex==0)return ret;int i,j;for(i=0;i<=rowIndex;i++){ret[i]=1;for(j=i-1;j>=1;j--){ret[j]=ret[j]+ret[j-1];}}return ret;}分析:
本题要求第rowindex行的所有杨辉三角数,可想到第rowindex行第i个数为从第一行开始不断向下求得出,即可以用一个for循环模拟这个过程,不断用ret[j]+ret[j-1]模拟上一行相同位置和前一位的数之和,最后输出ret
总结:
本题考察对题目的理解,将数用for循环表示出来即可解决
相关文章:

leetcode做题笔记119. 杨辉三角 II
给定一个非负索引 rowIndex,返回「杨辉三角」的第 rowIndex 行。 在「杨辉三角」中,每个数是它左上方和右上方的数的和。 思路一:模拟题意 int* getRow(int rowIndex, int* returnSize){int* ret malloc(sizeof(int)*(rowIndex1));ret[0]…...
Dolphin for Mac(Wii游戏模拟器)配置指南
Wii模拟器Dolphin Mac是款适合Mac电脑中的游戏玩家们使用的模拟器工具。Wii模拟器Dolphin Mac官方版支持直接运行游戏镜像文件,玩家可以将游戏ISO拷贝到某一个文件夹中统一进行管理。Wii模拟器Dolphin Mac除了键盘和鼠标外,还支持配合原版的Wii遥控器操作…...

Java,Linux,Mysql小白入门
Java入门 java后端__阿伟_的博客-CSDN博客 Linux与Git入门 Linux与Git入门教程__阿伟_的博客-CSDN博客 Mysql入门 Linux与Git入门教程__阿伟_的博客-CSDN博客...
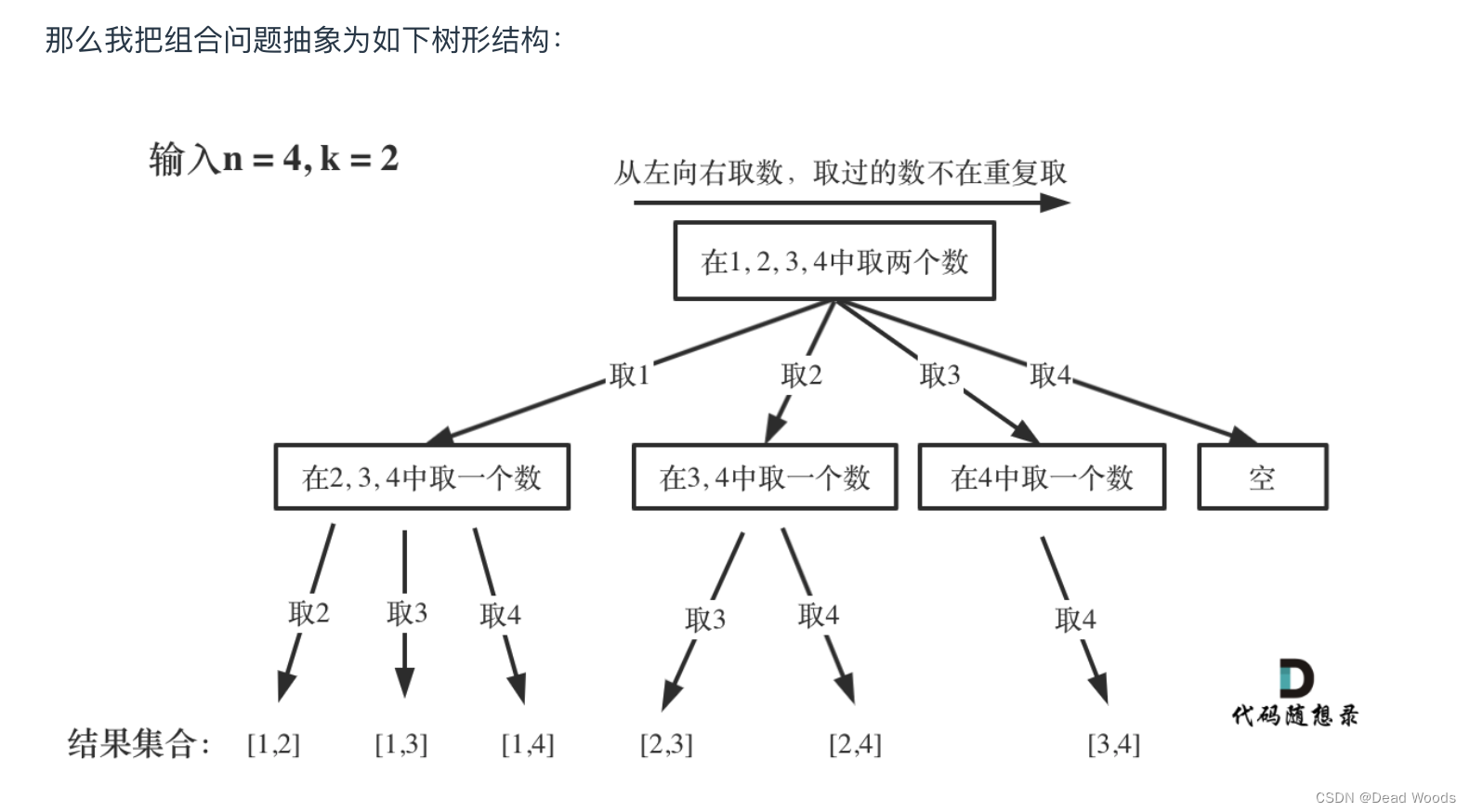
代码随想录算法训练营第二十四天|理论基础 77. 组合
理论基础 其实在讲解二叉树的时候,就给大家介绍过回溯,这次正式开启回溯算法,大家可以先看视频,对回溯算法有一个整体的了解。 题目链接/文章讲解:代码随想录 视频讲解:带你学透回溯算法(理论篇…...

macos安装zsh
https://www.cnblogs.com/xuLessReigns/p/11005435.html mac下安装autojump brew install autojump 1,安装zsh,执行 sh -c "$(curl -fsSL https://raw.github.com/robbyrussell/oh-my-zsh/master/tools/install.sh)" 2,将zsh设置…...
克隆体问题)
【Unity】预制体材质变(Clone)克隆体问题
1、排查代码是否存在直接修改预制体的材质为克隆体。 解决:删了这段代码。 2、双击Prefab文件进入预制体编辑模式时,会执行预制体身上的脚本方法Awake、Start等(生命周期方法),所以要排查这些方法里是否有克隆…...
python“魂牵”京东商品历史价格数据接口(含代码示例)
要通过京东的API获取商品详情历史价格数据,您可以使用京东开放平台提供的接口来实现。以下是一种使用Java编程语言实现的示例,展示如何通过京东开放平台API获取商品详情历史价格数据: 首先,确保您已注册成为京东开放平台的开发者…...
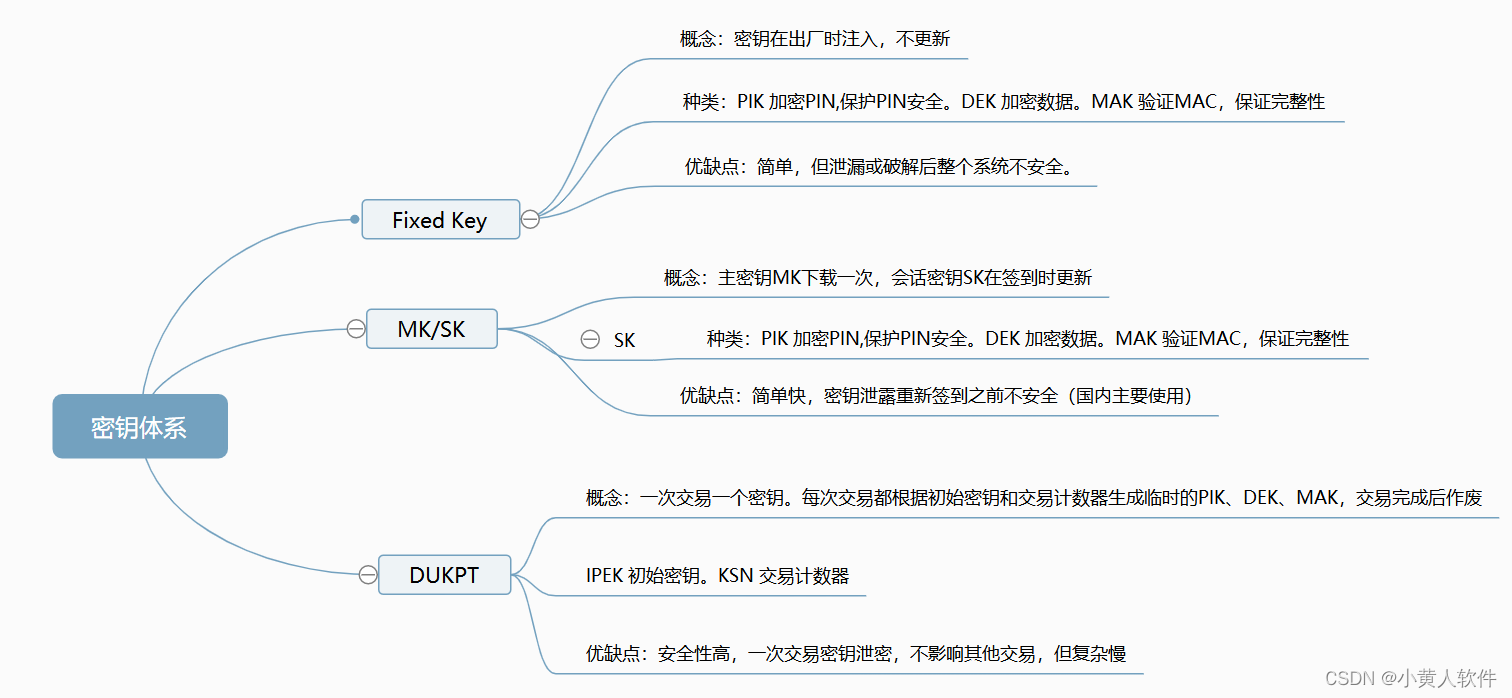
密码算法、密钥体系---安全行业基础篇1
一、密码算法 密码算法是一种数学和计算方法,用于保护数据的机密性和安全性。不同的密码算法使用不同的数学原理和技术来加密和解密数据。以下是一些常见的密码算法类型: 1. **对称密码算法:** 特点:相同的密钥用于加密和解密数…...

Java工具类记录
HTML转word 相关依赖 <dependency><groupId>org.apache.poi</groupId><artifactId>poi</artifactId><version>4.1.2</version></dependency>import org.apache.poi.poifs.filesystem.DirectoryEntry; import org.apache.poi…...
DVWA靶场搭建
目录 配置环境: 1、将下载好的压缩包放置php的WWW根目录下 2、改文件配置 3、查看mysql用户名和密码,将其修改值靶场配置文件中 4、完成后我们就可以在浏览器输入127.0.0.1/dvwa进入靶场 测试XSS注入: 配置环境: githhub下…...
uniapp语法1)
Uniapp笔记(二)uniapp语法1
一、本节项目预备知识 1、效果演示 2、常见组件 1、view组件 视图容器,它类似于传统html中的div,用于包裹各种元素内容。 2、swiper组件 swiper是滑动视图容器,经常看到的轮播图就是通过它来完成的 swiper-item是swiper子组件…...

【1day】PHPOK cms SQL注入学习
目录 一、漏洞描述 二、资产测绘 三、漏洞复现 四、漏洞修复 一、漏洞描述 PHPOK CMS是一个基于PHP语言开发的开源内容管理系统(CMS)。它提供了一个强大的平台,用于创建和管理网站内容。PHPOK CMS具有灵活的模块化架构,可以根据网站的需求进行定制和扩展。PHPOK CMS存…...

线程同步与互斥
目录 前言:基于多线程不安全并行抢票 一、线程互斥锁 mutex 1.1 加锁解锁处理多线程并发 1.2 如何看待锁 1.3 如何理解加锁解锁的本质 1.4 CRAII方格设计封装锁 前言:基于线程安全的不合理竞争资源 二、线程同步 1.1 线程同步处理抢票 1.2 如何…...
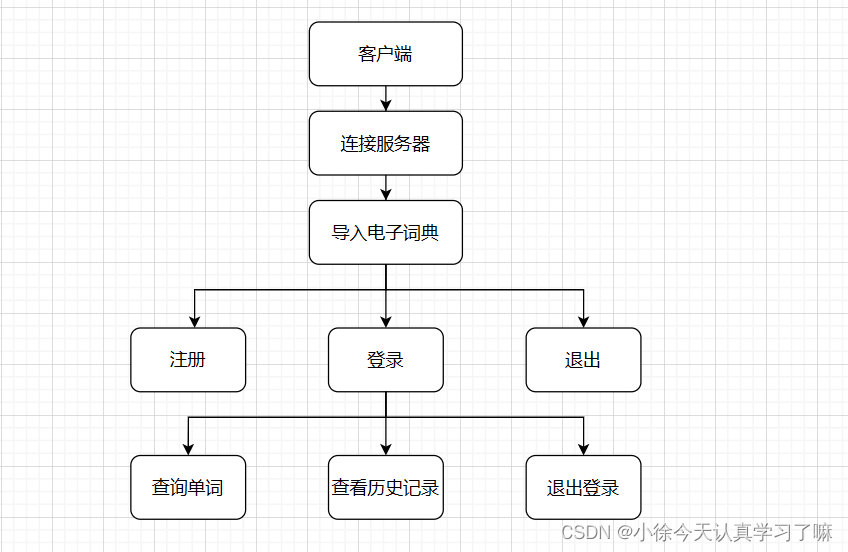
电子词典dictionary
一、项目要求: 1.登录注册功能,不能重复登录,重复注册。用户信息也存储在数据库中。 2.单词查询功能 3.历史记录功能,存储单词,意思,以及查询时间,存储在数据库 4.基于TCP,支持多客户…...
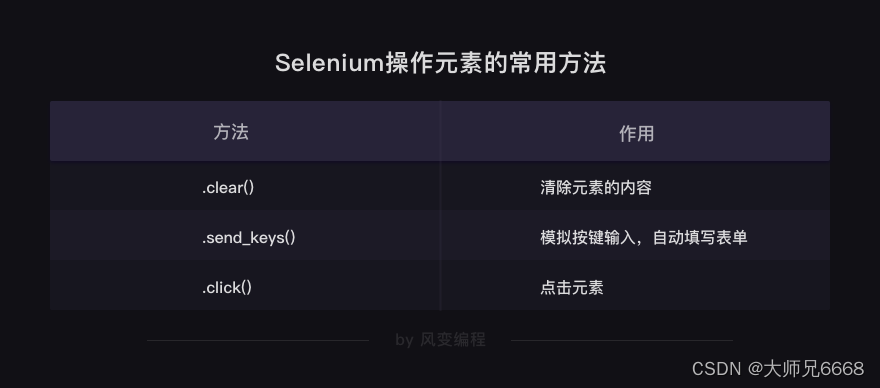
【python爬虫】10.指挥浏览器自动工作(selenium)
文章目录 前言selenium是什么怎么用设置浏览器引擎获取数据解析与提取数据自动操作浏览器 实操运用确认目标分析过程代码实现 本关总结 前言 上一关,我们认识了cookies和session。 分别学习了它们的用法,以及区别。 还做了一个项目:带着小…...
QT文件对话框,将标签内容保存至指定文件
一、主要步骤 首先,通过getSaveFileName过去想要保存的文件路径及文件名,其次,通过QFile类实例化一个文件对象,再读取文本框中的内容,最后将读取到的内容写入到文件中,最后关闭文件。 1.txt即为完成上述操作…...
C#,《小白学程序》第十一课:阶乘(Factorial)的计算方法与代码
1 文本格式 /// <summary> /// 阶乘的非递归算法 /// </summary> /// <param name"a"></param> /// <returns></returns> private int Factorial_Original(int a) { int r 1; for (int i a; i > 1; i--) { …...
MySQL 数据库常用命令大全(完整版)
文章目录 1. MySQL命令2. MySQL基础命令3. MySQL命令简介4. MySQL常用命令4.1 MySQL准备篇4.1.1 启动和停止MySQL服务4.1.2 修改MySQL账户密码4.1.3 MySQL的登陆和退出4.1.4 查看MySQL版本 4.2 DDL篇(数据定义)4.2.1 查询数据库4.2.2 创建数据库4.2.3 使…...

【数学】【书籍阅读笔记】【概率论】应用随机过程概率论模型导论 by Sheldon M.Ross 第一章 概率论引总结与习题题解 【更新中】
文章目录 前言1 第一章 概率论引论 总结1.1 样本空间与事件1.2 定义在事件上的概率1.3 条件概率1.4 独立事件 2 一些有用的重要结论/公式/例题3 重要例题例 1.11 3 习题题解题1题2 4 习题总结 前言 1 第一章 概率论引论 总结 第一章从事件的角度引出样本空间、事件、概率的基本…...

posexplode函数实战总结
目录 1、建表和准备数据 2、炸裂实践 3、错误炸裂方式 4、当字段类型为string,需要split一下 对单列array类型的字段进行炸裂时,可以使用lateral view explode。 对多列array类型的字段进行炸裂时,可以使用lateral view posexplode。 1…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...
