C#,《小白学程序》第十一课:阶乘(Factorial)的计算方法与代码
1 文本格式
/// <summary>
/// 阶乘的非递归算法
/// </summary>
/// <param name="a"></param>
/// <returns></returns>
private int Factorial_Original(int a)
{
int r = 1;
for (int i = a; i > 1; i--)
{
r = r * i;
}
return r;
}
/// <summary>
/// 阶乘的递归算法
/// 递归简单理解就是函数调用自己(当然参数不同哈!)
/// </summary>
/// <param name="a"></param>
/// <returns></returns>
private int Factorial(int a)
{
if (a > 1) return a * Factorial(a - 1);
else return 1;
}
/// <summary>
/// 《小白学程序》第十一课:阶乘(Factorial)的计算方法与代码
/// 阶乘是基斯顿·卡曼(Christian Kramp,1760~1826)于 1808 年发明的运算符号,是数学术语。
/// 一个正整数的阶乘(factorial)是所有小于及等于该数的正整数的积,并且0的阶乘为1。自然数n的阶乘写作n!。
/// 1808年,基斯顿·卡曼引进这个表示法。亦即 n! = 1×2×3×...×(n-1)×n。
/// 阶乘亦可以递归方式定义:
/// 0! = 1
/// n! = (n-1)! × n
///
/// 本节课接触了函数(阶乘函数)。
/// </summary>
/// <param name="sender"></param>
/// <param name="e"></param>
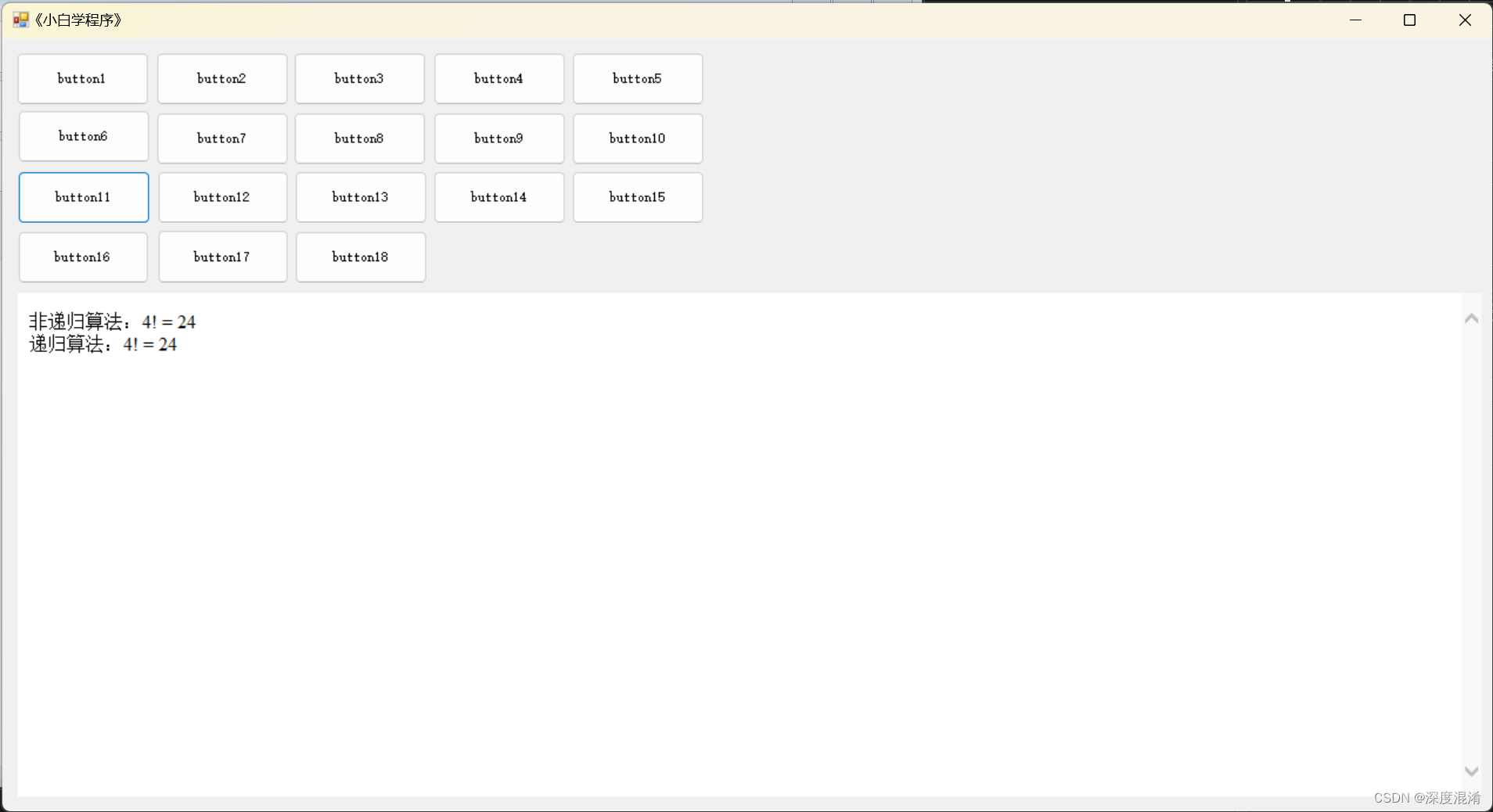
private void button11_Click(object sender, EventArgs e)
{
int n = 4;
StringBuilder sb = new StringBuilder();
sb.AppendLine("非递归算法:" + n + "! = " + Factorial_Original(n) + "<br>");
sb.AppendLine("递归算法:" + n + "! = " + Factorial(n) + "<br>");
webBrowser1.DocumentText = sb.ToString();
}
2 代码格式
/// <summary>
/// 阶乘的非递归算法
/// </summary>
/// <param name="a"></param>
/// <returns></returns>
private int Factorial_Original(int a)
{int r = 1;for (int i = a; i > 1; i--){r = r * i;}return r;
}/// <summary>
/// 阶乘的递归算法
/// 递归简单理解就是函数调用自己(当然参数不同哈!)
/// </summary>
/// <param name="a"></param>
/// <returns></returns>
private int Factorial(int a)
{if (a > 1) return a * Factorial(a - 1);else return 1;
}/// <summary>
/// 《小白学程序》第十一课:阶乘(Factorial)的计算方法与代码
/// 阶乘是基斯顿·卡曼(Christian Kramp,1760~1826)于 1808 年发明的运算符号,是数学术语。
/// 一个正整数的阶乘(factorial)是所有小于及等于该数的正整数的积,并且0的阶乘为1。自然数n的阶乘写作n!。
/// 1808年,基斯顿·卡曼引进这个表示法。亦即 n! = 1×2×3×...×(n-1)×n。
/// 阶乘亦可以递归方式定义:
/// 0! = 1
/// n! = (n-1)! × n
///
/// 本节课接触了函数(阶乘函数)。
/// </summary>
/// <param name="sender"></param>
/// <param name="e"></param>
private void button11_Click(object sender, EventArgs e)
{int n = 4;StringBuilder sb = new StringBuilder();sb.AppendLine("非递归算法:" + n + "! = " + Factorial_Original(n) + "<br>");sb.AppendLine("递归算法:" + n + "! = " + Factorial(n) + "<br>");webBrowser1.DocumentText = sb.ToString();
}
3 局限性
咱们尝试着计算其他数据的阶乘:
16! = 2004189184
17! = -288522240
可见,上面的算法无法计算超过 16 的阶乘!!!!
将数据类型改为 long 可以计算更大的阶乘。
private long Factorial(long a)
{if (a > 1) return a * Factorial(a - 1);else return 1;
}
20! = 2432902008176640000
21! = -4249290049419214848
超过 20 又不行了!
怎么办?
后面学习 大数的乘法,可计算很大数的阶乘。
4 512 阶乘
512! = 347728979313260536328304591754560471199225065564351457034247483155161041206635254347320985033950225364432243311021394545295001702070069013264153113260937941358711864044716186861040899557497361427588282356254968425012480396855239725120562512065555822121708786443620799246550959187232026838081415178588172535280020786313470076859739980965720873849904291373826841584712798618430387338042329771801724767691095019545758986942732515033551529595009876999279553931070378592917099002397061907147143424113252117585950817850896618433994140232823316432187410356341262386332496954319973130407342567282027398579382543048456876800862349928140411905431276197435674603281842530744177527365885721629512253872386613118821540847897493107398381956081763695236422795880296204301770808809477147632428639299038833046264585834888158847387737841843413664892833586209196366979775748895821826924040057845140287522238675082137570315954526727437094904914796782641000740777897919134093393530422760955140211387173650047358347353379234387609261306673773281412893026941927424000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
5 1024阶乘
1024! = 541852879605885728307692194468385473800155396353801344448287027068321061207337660373314098413621458671907918845708980753931994165770187368260454133333721939108367528012764993769768292516937891165755680659663747947314518404886677672556125188694335251213677274521963430770133713205796248433128870088436171654690237518390452944732277808402932158722061853806162806063925435310822186848239287130261690914211362251144684713888587881629252104046295315949943900357882410243934315037444113890806181406210863953275235375885018598451582229599654558541242789130902486944298610923153307579131675745146436304024890820442907734561827369030502252796926553072967370990758747793127635104702469889667961462133026237158973227857814631807156427767644064591085076564783456324457736853810336981776080498707767046394272605341416779125697733374568037475186676265961665615884681450263337042522664141862157046825684773360944326737493676674915098953768112945831626643856479027816385730291542667725665642276826058264393884514911976419675509290208592713156362983290989441052732125187249527501314071676405516936190781821236701912295767363117054126589929916482008515781751955466910902838729232224509906388638147771255227782631322385756948819393658889908993670874516860653098411020299853816281564334981847105777839534742531499622103488807584513705769839763993103929665046046121166651345131149513657400869056334867859885025601787284982567787314407216524272262997319791568603629406624740101482697559533155736658800562921274680657285201570401940692285557800611429055755324549794008939849146812639860750085263298820224719585505344773711590656682821041417265040658600683844945104354998812886801316551551714673388323340851763819713591312372548673734783537316341517369387565212899726597964903241208727348690699802996369265070088758384854547542272771024255049902319275830918157448205196421072837204937293516175341957775422453152442280391372407717891661203061040255830055033886790052116025408740454620938384367637886658769912790922323717371343176067483352513629123362885893627132294183565884010418727869354439077085278288558308427090461075019007184933139915558212752392329879780649639075333845719173822840501869570463626600235265587502335595489311637509380219119860471335771652403999403296360245577257963673286654348957325740999710567131623272345766761937651408103999193633908286420510098577454524068106897392493138287362226257920000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
相关文章:

C#,《小白学程序》第十一课:阶乘(Factorial)的计算方法与代码
1 文本格式 /// <summary> /// 阶乘的非递归算法 /// </summary> /// <param name"a"></param> /// <returns></returns> private int Factorial_Original(int a) { int r 1; for (int i a; i > 1; i--) { …...
MySQL 数据库常用命令大全(完整版)
文章目录 1. MySQL命令2. MySQL基础命令3. MySQL命令简介4. MySQL常用命令4.1 MySQL准备篇4.1.1 启动和停止MySQL服务4.1.2 修改MySQL账户密码4.1.3 MySQL的登陆和退出4.1.4 查看MySQL版本 4.2 DDL篇(数据定义)4.2.1 查询数据库4.2.2 创建数据库4.2.3 使…...

【数学】【书籍阅读笔记】【概率论】应用随机过程概率论模型导论 by Sheldon M.Ross 第一章 概率论引总结与习题题解 【更新中】
文章目录 前言1 第一章 概率论引论 总结1.1 样本空间与事件1.2 定义在事件上的概率1.3 条件概率1.4 独立事件 2 一些有用的重要结论/公式/例题3 重要例题例 1.11 3 习题题解题1题2 4 习题总结 前言 1 第一章 概率论引论 总结 第一章从事件的角度引出样本空间、事件、概率的基本…...

posexplode函数实战总结
目录 1、建表和准备数据 2、炸裂实践 3、错误炸裂方式 4、当字段类型为string,需要split一下 对单列array类型的字段进行炸裂时,可以使用lateral view explode。 对多列array类型的字段进行炸裂时,可以使用lateral view posexplode。 1…...
QTday3(对话框、发布软件、事件处理核心机制)
一、Xmind整理: 二、上课笔记整理: 1.消息对话框(QMessageBox) ①基于属性版本的API QMessageBox::QMessageBox( //有参构造函数名QMessageBox::Icon icon, //图标const Q…...
el-date-picker限制选择的时间范围
<el-date-pickersize"mini"v-model"dateTime"value-format"yyyy-MM-dd HH:mm:ss"type"datetimerange"range-separator"~"start-placeholder"开始日期"end-placeholder"结束日期":picker-options&quo…...

Scala中的Actor模型
Scala中的Actor模型 概念 Actor Model是用来编写并行计算或分布式系统的高层次抽象(类似java中的Thread)让程序员不必为多线程模式下共享锁而烦恼。Actors将状态和行为封装在一个轻量的进程/线程中,但是不和其他Actors分享状态,…...
Java使用pdfbox将pdf转图片
前言 目前比较主流的两种转pdf的方式,就是pdfbox和icepdf,两种我都尝试了下,icepdf解析出来有时候会出现中文显示不出来,网上的解决方式又特别麻烦,不是安装字体,就是重写底层类,所以我选择了p…...

大规模场景下对Istio的性能优化
简介 当前istio下发xDS使用的是全量下发策略,也就是网格里的所有sidecar(envoy),内存里都会有整个网格内所有的服务发现数据。这样的结果是,每个sidecar内存都会随着网格规模增长而增长。 Aeraki-mesh aeraki-mesh项目下有一个子项目专门用来…...

数字化新零售平台系统提供商,门店商品信息智慧管理-亿发进销存
传统的批发零售业务模式正面临着市场需求变化的冲击。用户日益注重个性化、便捷性和体验感,新兴的新零售模式迅速崛起,改变了传统的零售格局。如何在保持传统业务的基础上,变革发展,成为了业界亟需解决的问题。 在这一背景下&…...
postgresql-窗口函数
postgresql-窗口函数 简介窗口函数的定义分区选项(PARTITION BY)排序选项(ORDER BY)窗口选项(frame_clause) 聚合窗口函数排名窗口函数演示了 CUME_DIST 和 NTILE 函数 取值窗口函数 简介 常见的聚合函数&…...
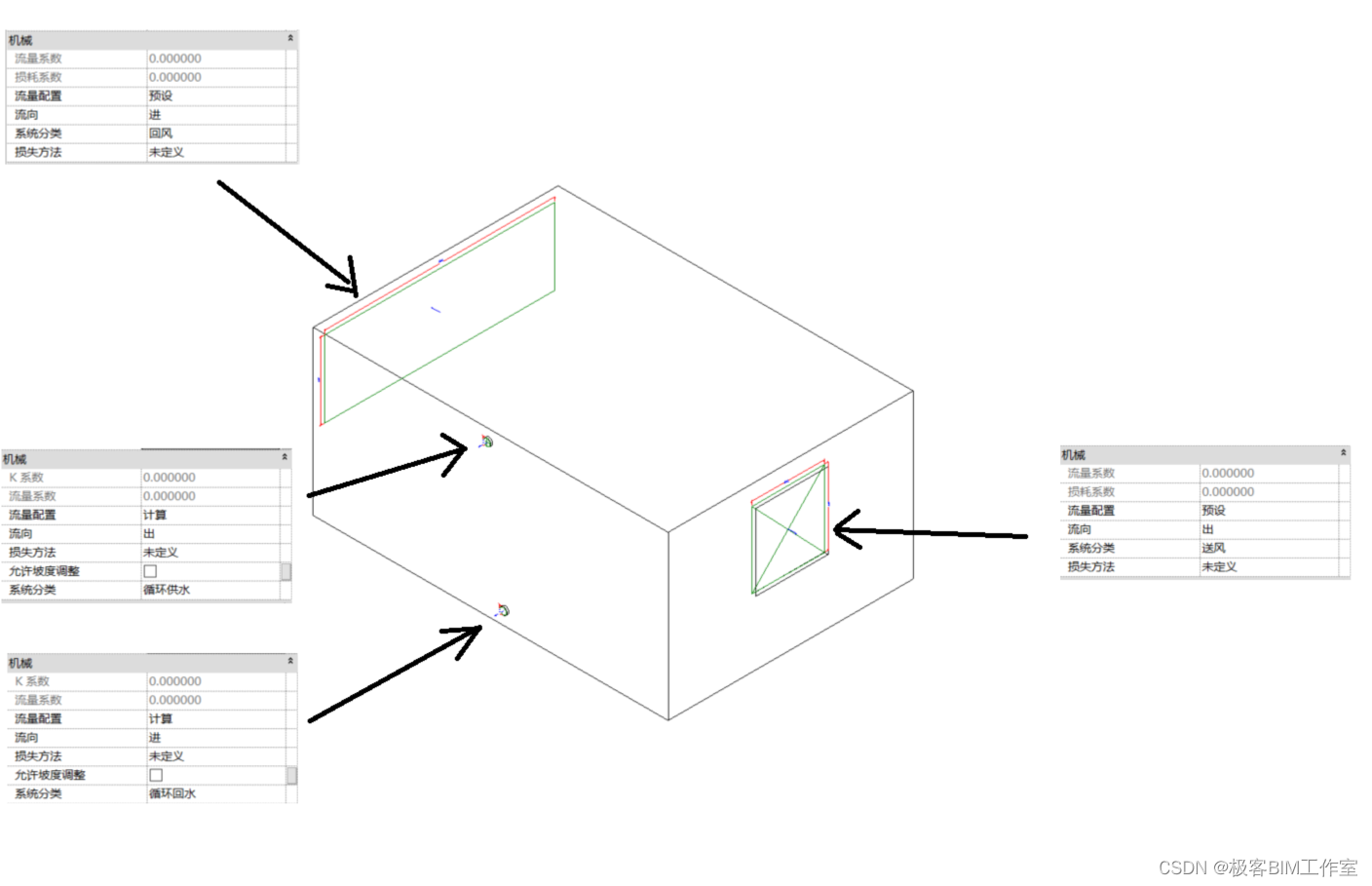
Revit SDK 介绍:CreateAirHandler 创建户式风管机
前言 这个例子介绍如何通过 API 创建一个户式风管机族的内容,包含几何和接头。 内容 效果 核心逻辑 必须打开机械设备的族模板创建几何实体来表示风管机创建风机的接头 创建几何实体来表示风管机 例子中创建了多个拉伸,下面仅截取一段代码ÿ…...

微信小程序云开发-云函数发起https请求简易封装函数
一、前言 在日常的开发中,经常会遇到需要请求第三方API的情况,例如请求实名认证接口、IP转换地址接口等等。这些请求放在小程序前端的话,就需要把密钥放在客户端,在安全性上没这么高。 因此,一般是放在云函数端去访问…...

深入探索PHP编程:连接数据库的完整指南
深入探索PHP编程:连接数据库的完整指南 在现代Web开发中,与数据库进行交互是不可或缺的一部分。PHP作为一种强大的服务器端编程语言,提供了丰富的工具来连接和操作各种数据库系统。本篇教程将带您了解如何在PHP中连接数据库,执行…...
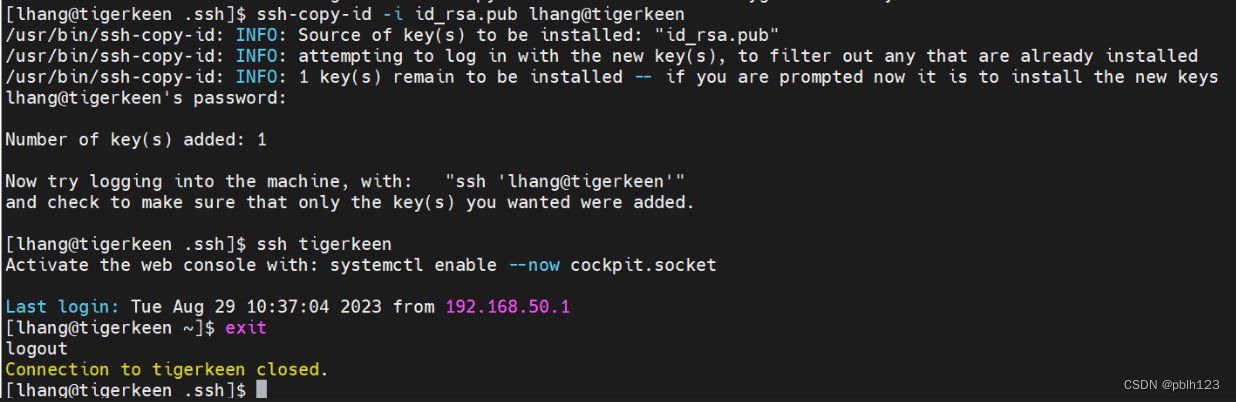
【Centos8配置节点免密登陆】
登录Centos8 配置免密登录 为什么需要配置免密登录,玩大数据,玩集群的朋友们,都需要使用RPC通讯,完成集群命令同步,数据操作通讯。要实现RPC通讯,就需要配置节点之间的免密登录。 # 配置登录秘钥 ssh-key…...
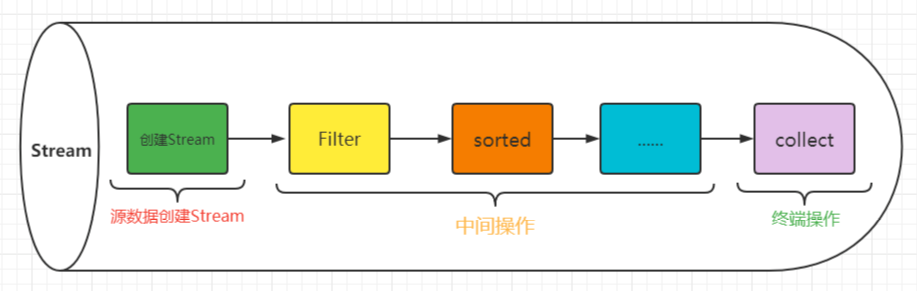
不可变集合、Lambda表达式、Stream流
不可变集合、Lambda表达式、Stream流 创建不可变集合 不能被修改的集合 应用场景 如果某个数据不能被修改,把它防御性的拷贝到不可变集合中是个很好的实践。 当集合对象被不可信的库调用时,不可变形式是安全的。 创建不可变集合 在List、Set、Map接口中…...

Three.js GLTF模型加载
在Three.js中,要加载三维模型文件,可以使用GLTF格式。GLTF是一种基于JSON的开放标准,用于3D模型的交换和运行时加载。本篇文章将详细讲解如何使用Three.js加载GLTF模型。 ## 1. 下载GLTF模型 在开始之前,请确保您已经有一个GLTF模…...
外包干了2个月,技术退步明显...
先说一下自己的情况,大专生,18年通过校招进入湖南某软件公司,干了接近4年的功能测试,今年年初,感觉自己不能够在这样下去了,长时间呆在一个舒适的环境会让一个人堕落!而我已经在一个企业干了四年的功能测试…...
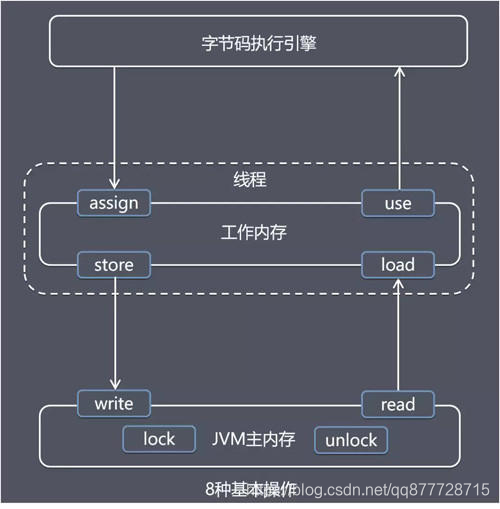
java八股文面试[多线程]——主内存和工作内存的关系
JAVA内存模型(JMM)共享变量:如果一个变量在多个线程的工作内存中都存在副本,那么这个变量就是这几个线程的共享变量。 上面的工作内存其实是java内存模型抽象出来的概念,下面简要介绍一下java内存模型(JMM&…...

技术分享 | LSM,Linux 内核的安全防护盾
计算机安全是一个非常重要的概念和主题,它不仅仅可以保护用户个人信息和资产的安全,还可以影响到用户在使用过程中的体验;但同时,它也是一个很抽象的概念,关于其相关文献和资料不计其数,但它究竟是什么、包…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...
