数据结构:时间复杂度和空间复杂度计算
1.什么是时间复杂度和空间复杂度?
1.1算法效率
算法效率分析分为两种:第一种是时间效率,第二种是空间效率。时间效率被称为时间复杂度,
而空间效率被称作空间复杂度。 时间复杂度主要衡量的是一个算法的运行速度,而空间复杂度主
要衡量一个算法所需要的额外空间,在计算机发展的早期,计算机的存储容量很小。所以对空间
复杂度很是在乎。但是经过计算机行业的迅速发展,计算机的存储容量已经达到了很高的程度。
所以我们如今已经不需要再特别关注一个算法的空间复杂度。
1.2 时间复杂度的概念
时间复杂度的定义:在计算机科学中,算法的时间复杂度是一个函数,它定量描述了该算法的运
行时间。一个算法执行所耗费的时间,从理论上说,是不能算出来的,只有你把你的程序放在机
器上跑起来,才能知道。但是我们需要每个算法都上机测试吗?是可以都上机测试,但是这很麻
烦,所以才有了时间复杂度这个分析方式。一个算法所花费的时间与其中语句的执行次数成正比
例,算法中的基本操作的执行次数,为算法的时间复杂度。
1.3 空间复杂度的概念
空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度 。空间复杂度不是程序占用
了多少bytes的空间,因为这个也没太大意义,所以空间复杂度算的是变量的个数。空间复杂度计
算规则基本跟实践复杂度类似,也使用大O渐进表示法。
大O的渐进表示法
#include <stdio.h>// 请计算一下Func1基本操作执行了多少次?
void Func1(int N)
{int count = 0;for (int i = 0; i < N; ++i){for (int j = 0; j < N; ++j){++count;}}for (int k = 0; k < 2 * N; ++k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}Func1 执行的基本操作次数 :F(N)=N^2+N*2+10
实际中我们计算时间复杂度时,我们其实并不一定要计算精确的执行次数,而只需要大概执行次数,那么这里我们使用大O的渐进表示法。大O符号(Big O notation):是用于描述函数渐进行为的数学符号。
推导大O阶方法:
1、用常数1取代运行时间中的所有加法常数。
2、在修改后的运行次数函数中,只保留最高阶项。
3、如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶。
使用大O的渐进表示法以后,Func1的时间复杂度为:O(N^2)
N = 10 F(N) = 100
N = 100 F(N) = 10000
N = 1000 F(N) = 1000000
通过上面我们会发现大O的渐进表示法去掉了那些对结果影响不大的项,简洁明了的表示出了执
行次数。
另外有些算法的时间复杂度存在最好、平均和最坏情况:
最坏情况:任意输入规模的最大运行次数(上界)
平均情况:任意输入规模的期望运行次数
最好情况:任意输入规模的最小运行次数(下界)
例如:在一个长度为N数组中搜索一个数据x
最好情况:1次找到
最坏情况:N次找到
平均情况:N/2次找到
在实际中一般情况关注的是算法的最坏运行情况,所以数组中搜索数据时间复杂度为O(N)
2.时间复杂度与空间复杂度的区别
时间复杂度:
判断算法的时间复杂度通常是通过分析算法中的基本操作次数来进行的。以下是一些常用的判断时间复杂度的方法:
1. 计算操作的执行次数:根据算法的实际代码或伪代码,计算出每个操作(比如循环、条件判断、函数调用等)在最坏情况下执行的次数。
2. 识别循环结构:对于循环结构,需要确定循环的迭代次数,并将循环体中的操作次数乘以迭代次数。
3. 分析递归算法:对于递归算法,可以使用递归树或递归方程的方法来进行分析,推导出递归的深度和每层的操作次数。
4. 考虑最坏情况:时间复杂度通常使用算法最坏情况下的操作次数来表示,这样可以保证算法在任何情况下的时间表现。
5. 忽略常数项和低阶项:在计算时间复杂度时,通常忽略操作次数的常数项和低阶项,只保留最高阶的项,使用大O符号表示。
需要注意的是,时间复杂度只是对算法的一个粗略估计,它描述的是算法运行时间与输入规模的增长趋势,并不具体表示实际的执行时间。此外,时间复杂度是在理论上对算法效率的分析,实际运行时的表现可能受到各种因素影响。
因此,在分析时间复杂度时,需要结合具体的算法实现、输入规模以及实际的运行环境等因素来进行判断和评估。
空间复杂度
判断算法的空间复杂度通常是通过分析算法在执行过程中所需的额外空间来进行的。以下是一些常用的判断空间复杂度的方法:
1. 计算变量占用的空间:根据算法中定义的变量、数据结构和临时存储空间等,计算出在最坏情况下所需的额外空间。
2. 考虑递归函数调用栈:对于使用递归的算法,需要考虑递归函数调用时占用的栈空间。
3. 分析数据结构的空间复杂度:对于使用的数据结构(如数组、链表、栈、队列等),需要根据其存储方式和元素数量来分析其占用的额外空间。
4. 考虑函数调用和递归深度:在算法执行过程中,如果有函数调用或递归调用,需要考虑每次调用时所需的栈空间。
5. 忽略常数项和低阶项:与时间复杂度类似,空间复杂度的计算中通常忽略常数项和低阶项,只保留最高阶的项,使用大O符号表示。
需要注意的是,空间复杂度表示的是算法在执行过程中所需的额外空间,而不是算法所操作的原始输入数据的空间。因此,在计算空间复杂度时,应将注意力放在算法运行过程中所需额外空间的分析上。
与时间复杂度类似,空间复杂度也只是对算法的一个粗略估计,它描述的是算法所需额外空间随输入规模的增长趋势,并不具体表示实际的空间使用情况。在实际应用中,也要结合具体的算法实现、数据规模以及可用内存等因素来进行判断和评估。
二者的区别
时间复杂度和空间复杂度是用来衡量算法效率的两个重要指标。它们分别关注算法在执行过程中所需的时间和空间资源消耗。
时间复杂度(Time Complexity)衡量的是算法执行所需的时间,也可以说是算法的运行时间。它描述的是算法执行所消耗的操作步骤数量与输入规模之间的关系。常用大O符号(O)表示时间复杂度。
时间复杂度反映了算法在处理数据时所需的时间随着输入规模的增加而增长的速度。一般来说,时间复杂度越低,算法的执行效率越高。常见的时间复杂度包括常数时间O(1)、线性时间O(n)、对数时间O(log n)、平方时间O(n^2)等。
空间复杂度(Space Complexity)衡量的是算法执行所需的额外空间,也可以说是算法的存储空间。它描述的是算法所需的额外空间与输入规模之间的关系。同样,常用大O符号(O)表示空间复杂度。
空间复杂度反映了算法在处理数据时所需的额外空间随着输入规模的增加而增长的速度。一般来说,空间复杂度越低,算法所需的额外空间越小。常见的空间复杂度包括常数空间O(1)、线性空间O(n)、对数空间O(log n)等。
需要注意的是,时间复杂度和空间复杂度是独立且不可兼得的。某个算法可能在时间复杂度上表现良好,但在空间复杂度上较高,或者反之。因此,在选择算法时,需要根据实际情况综合考虑时间和空间的权衡。
相关文章:

数据结构:时间复杂度和空间复杂度计算
1.什么是时间复杂度和空间复杂度? 1.1算法效率 算法效率分析分为两种:第一种是时间效率,第二种是空间效率。时间效率被称为时间复杂度, 而空间效率被称作空间复杂度。 时间复杂度主要衡量的是一个算法的运行速度,而空间…...

云原生Kubernetes:二进制部署K8S单Master架构(一)
目录 一、理论 1.K8S单Master架构 2. etcd 集群 3.flannel网络 4.K8S单Master架构环境部署 5.部署 etcd 集群 6.部署 docker 引擎 7.flannel网络配置 二、实验 1.二进制部署K8S单Master架构 2. 环境部署 3.部署 etcd 集群 4.部署 docker 引擎 5.flannel网络配置…...
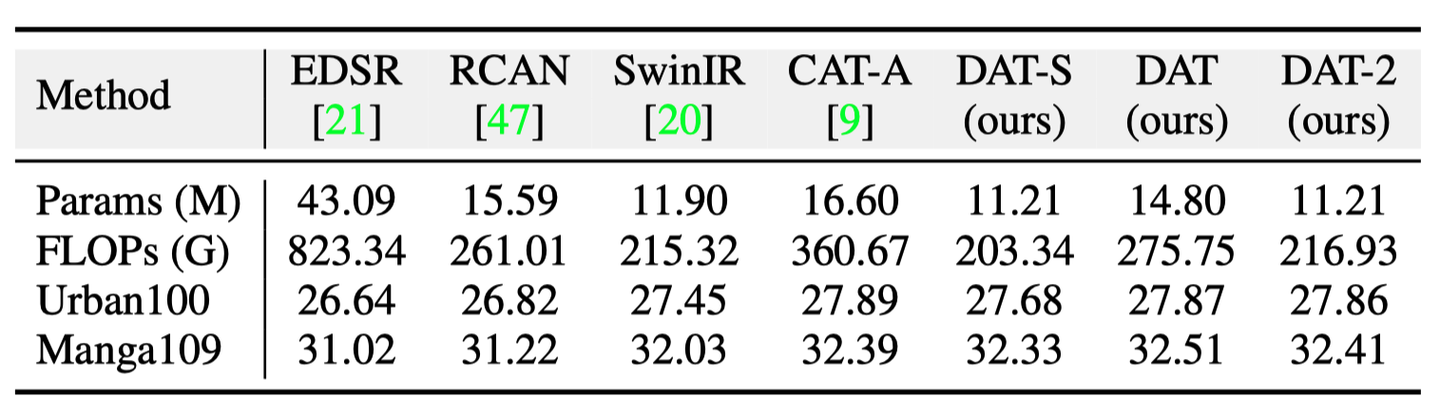
ICCV 2023 | 利用双重聚合的Transformer进行图像超分辨率
导读 本文提出一种同时利用图像空间和通道特征的 Transformer 模型,DAT(Dual Aggregation Transformer),用于图像超分辨(Super-Resolution,SR)任务。DAT 以块间和块内的双重方式,在空…...
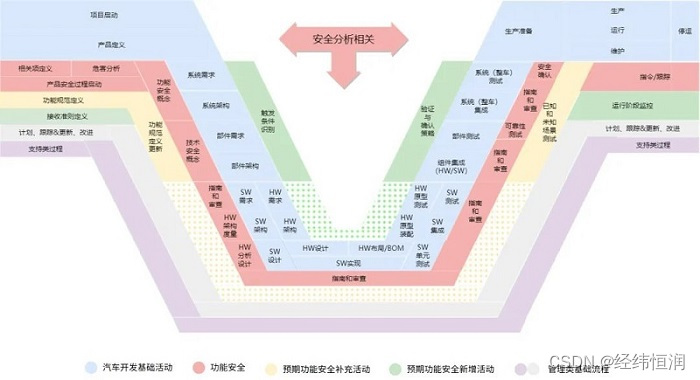
经纬恒润预期功能安全(SOTIF)解决方案为自动驾驶安全保驾护航
近年来,“安全”被普遍认为是智能驾驶汽车被用户接受或者得到商业应用最大的问题,ISO26262功能安全旨在避免由E/E系统功能失效导致的不可接受的风险,主要是针对系统性失效/随机硬件失效导致的风险进行分析和控制,然而传感器和感知…...
——面向对象)
java从入门到起飞(七)——面向对象
文章目录 一、什么是面向对象1.1 定义1.2 特点 二、面向对象的基础2.1 面向对象的基础是抽象2.2 抽象的作用2.3 类和对象2.4 属性和方法2.5 构造方法 三、面向对象的三大特征3.1 封装3.1.1 封装的意义3.1.2 封装的实现 3.2 继承3.2.1 继承的意义3.2.2 继承的实现 3.3 多态3.3.1…...

题集-三路划分和三数取中(快排优化)
快排排序是非常快的,但是有一种情况快排是无法进行的。 912. 排序数组 - 力扣(LeetCode) 这道题看上去没什么问题,但是如果我们用快排去提交的话,发现快排其实是被针对了的。 有一个样例是这样的。如果我们按照快排的…...
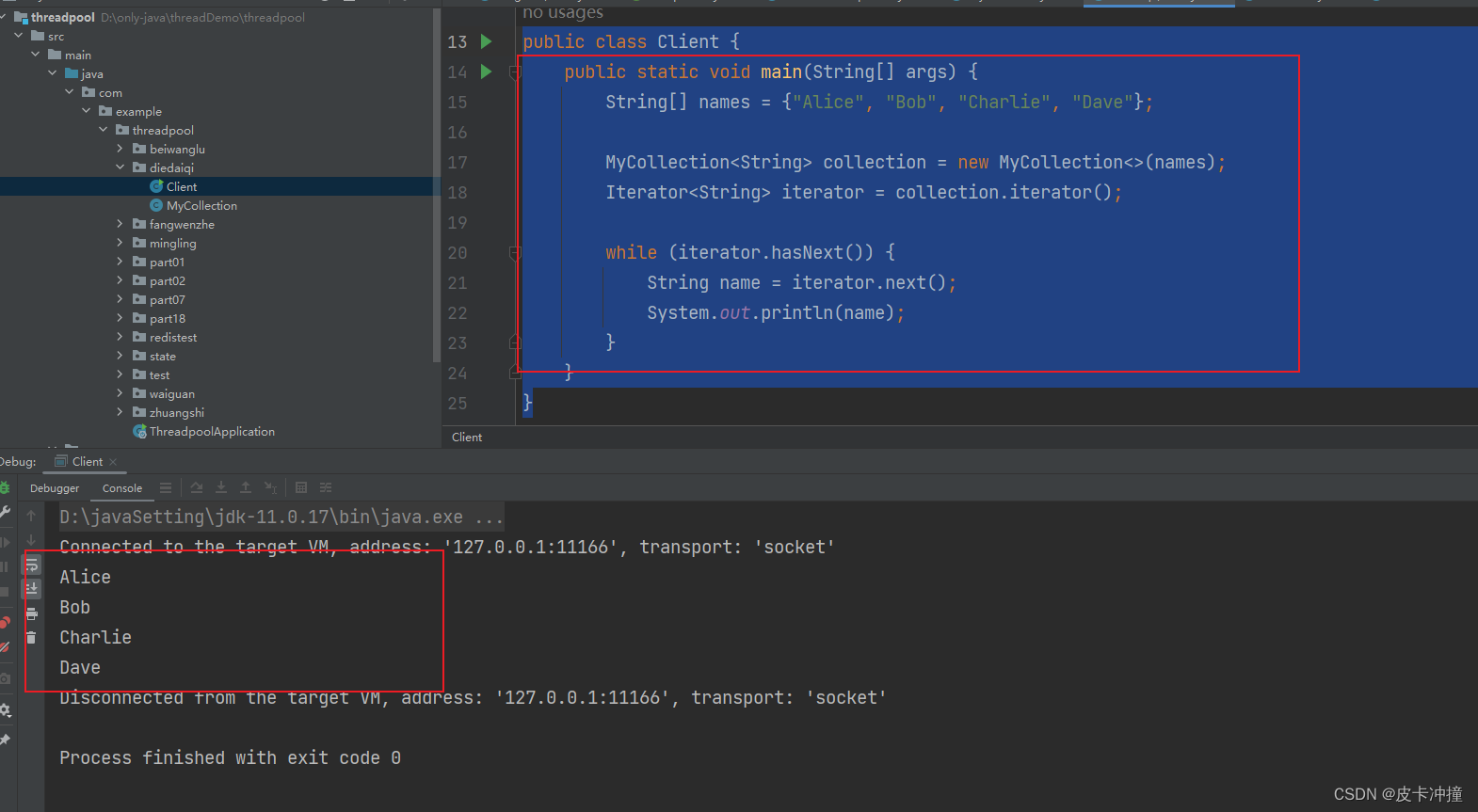
设计模式-迭代器
文章目录 1. 引言1.1 概述1.2 设计模式1.3 迭代器模式的应用场景1.4 迭代器模式的作用 2. 基本概念2.1 迭代器 Iterator2.2 聚合 Aggregate2.3 具体聚合 ConcreteAggregate 3. Java 实现迭代器模式3.1 Java 集合框架3.2 Java 迭代器接口3.3 Java 迭代器模式实现示例 4. 迭代器模…...
Hive常用日期函数)
Hive学习(12)Hive常用日期函数
1、hive返回当天三种方式 select current_date; --返回年月日 --2017-06-15 select current_timestamp; --返回年月日时分秒 --2017-06-15 19:54:44 SELECT from_unixtime(unix_timestamp()); --2017-06-15 19:55:042、from_unixtime:转化unix时间戳到当前时区的时…...
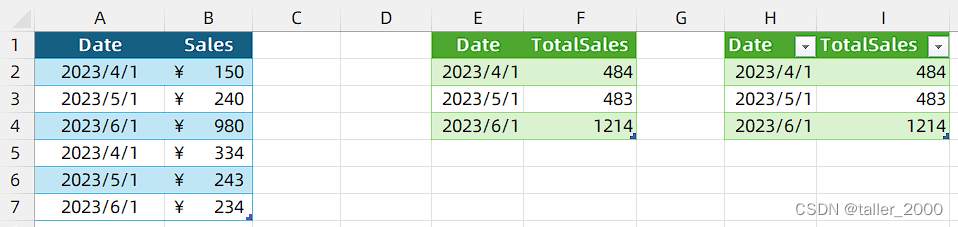
PowerQuery动态加载M公式
Power Query 是Excel中的强大数据处理与转换工具,如果需要“动态”处理数据,大家第一时间想到的是可以使用VBA,利用代码创建M公式,进而创建PQ查询,但是复杂的M公式可能有很多行, 使用VBA处理起来并不是很方…...
2分钟搭建FastGPT训练企业知识库AI助理(Docker部署)
我们使用宝塔面板来进行搭建,更方便快捷灵活,争取操作时间只需两分钟 宝塔面板下安装Docker 在【软件商店中】安装【docker管理器】【docker模块】即可 通过Docker安装FastGPT 通过【Docker】【添加容器】【容器编排】创建里新增docker-compose.yaml以下…...

TDengine函数大全-字符串函数
以下内容来自 TDengine 官方文档 及 GitHub 内容 。 以下所有示例基于 TDengine 3.1.0.3 TDengine函数大全 1.数学函数 2.字符串函数 3.转换函数 4.时间和日期函数 5.聚合函数 6.选择函数 7.时序数据库特有函数 8.系统函数 字符串函数 TDengine函数大全CHAR_LENGTHCONCATCONCA…...
)
part-02 C++知识总结(类型转换)
一.C常用的类型转换函数 在C中,有几种自带的类型转换函数可以用于不同类型之间的转换。以下是其中一些常用的自带类型转换函数: 1.隐式转换(Implicit Conversion) 数字类型之间的隐式转换,例如将int转换为float、do…...

stable diffusion实践操作-图生图
本文专门开一节写图生图相关的内容,在看之前,可以同步关注: stable diffusion实践操作 正文...

Jtti:Ubuntu18.04如何修改远程ssh端口号
要在Ubuntu 18.04上修改SSH的远程端口号,您需要编辑SSH服务器配置文件并指定新的端口号。以下是具体的步骤: 以root或具有sudo权限的用户登录到您的Ubuntu服务器。 备份SSH配置文件(可选): 在进行任何更改之前&…...
微软表示Visual Studio的IDE即日起开启“退休”倒计时
据了解,日前有消息透露称,适用于 Mac平台的Visual Studio集成开发环境(IDE)于8月31日启动“退休”进程。 而这意味着Visual Studio for Mac 17.6将继续支持12个月,一直到2024年8月31日。 微软表示后续不再为Visual Studio for Mac开发…...

好马配好鞍:Linux Kernel 4.12 正式发布
Linus Torvalds 在内核邮件列表上宣布释出 Linux 4.12,Linux 4.12 的主要特性包括: BFQ 和 Kyber block I/O 调度器,livepatch 改用混合一致性模型,信任的执行环境框架,epoll 加入 busy poll 支持等等,其它…...

element——switch接口成功后赋值打开开关
应用场景 基本用法使用v-model双向绑定值,进行开关控制 例子1:需求: **点击switch,出弹窗,点击弹窗保存按钮调接口成功后再赋值(row.orderButtonValue“1”)打开switch开的状态变颜色。 在vue 中使用 :va…...

WPF Border设置渐变色
背景色渐变 <Border> <Border.Resources> <Style TargetType"Border"> <Setter Property"Background"> …...
SAP_ABAP_OLE_EXCEL批导案例
SAP ABAP顾问能力模型梳理_企业数字化建设者的博客-CSDN博客SAP Abap顾问能力模型https://blog.csdn.net/java_zhong1990/article/details/132469977 一、OLE_EXCEL批导 1.1 下载按钮 1.2 选择EXCEL上传,解析EXCLE数据, Call屏幕。 1.3 实现效果 1.4…...
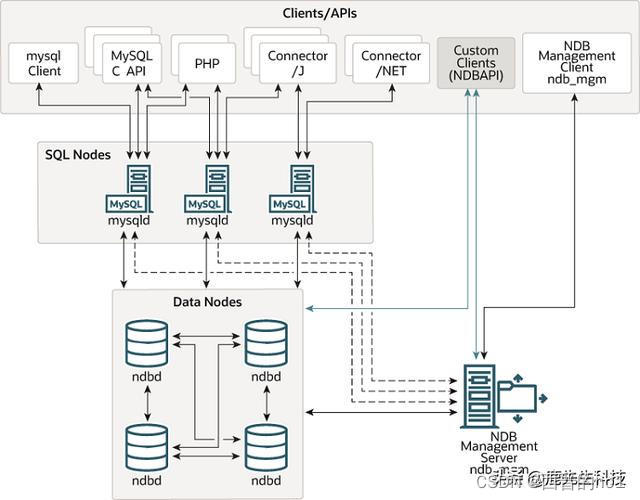
MySQL以及版本介绍
一、MySQL的介绍 MySQL数据库管理系统由瑞典的DataKonsultAB公司研发,该公司被Sun公司收购,现在Sun公司又被Oracle公司收购,因此MySQL目前属于 Oracle 旗下产品。 MySQL所使用的 SQL 语言是用于访问数据库的最常用标准化语言。MySQL 软件采用…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...
