鲁棒优化入门(7)—Matlab+Yalmip两阶段鲁棒优化通用编程指南(下)
0.引言
上一篇博客介绍了使用Yalmip工具箱求解单阶段鲁棒优化的方法。这篇文章将和大家一起继续研究如何使用Yalmip工具箱求解两阶段鲁棒优化(默认看到这篇博客时已经有一定的基础了,如果没有可以看看我专栏里的其他文章)。关于两阶段鲁棒优化与列与约束生成算法的原理,之前的博客已经详细地介绍过了,这里就不再过多介绍,主要是结合实例来讲解编程思路。这篇博客用到了两个算例,1个是两阶段鲁棒优化问题和列与约束生成算法的开山鼻祖[1],另一个是电气专业中两阶段鲁棒优化问题最热门的文章之一[2],相信大家在网上见到过无数号称完美复现的代码,但实际上大部分都是有问题的(包括我自己早期写的代码,也是被网上的代码带歪了,后面理解慢慢深入才发现问题所在)。
求解两阶段鲁棒优化问题一共有两个难点,一是求解max-min或者min-max形式的子问题,其实就是求解一个单阶段鲁棒优化,上一篇博客我已经非常详细地介绍了求解方式,借助Yalmip工具箱,共有三种不同的方式可以解决。二是主问题和子问题的迭代求解,也就是列与约束生成算法(C&CG)的实现。很多代码在复现C&CG算法时并没有向主问题同时添加列(变量)和约束,这也是代码中最常见的问题。针对这两个难点,我将用两个不同的算例详细地进行讲解。
此外,文献[1]和[2]中都是采用了先将约束条件写成紧凑的矩阵形式,然后再对子问题进行处理的方式,很多朋友和我反映这部分太难处理了,实际问题的约束建模过程中经常包括循环语句,想要转成矩阵形式确实很不容易。这篇文章中我将分别采用两种不同的方式求解鲁棒优化。一是采用原始的约束条件,省去将约束条件转为矩阵形式的步骤,这种方式数学公式可能会更繁琐,但比起矩阵形式的转换,理解起来会更容易一些。二是采用矩阵形式进行编程,在博客中我教大家一种非常简单就能将约束写为矩阵形式的方法,文中只是介绍了如何使用,之后也会单独写博客对此详细展开。
总之,这篇博客干货满满,可以认真通读一遍,跟着博客中的思路亲自动手使用Matlab+Yalmip实现两阶段鲁棒优化的编程(博客中提到的所有例子我都提供了相应的代码)。相信大家理解后,面对任何类型的两阶段鲁棒优化问题都能迅速使用类似的方法进行解决。
博客中主要包含8大内容:
①.拿到一个复杂的两阶段鲁棒优化问题的分析步骤和方法。
②.采用Yalmip工具箱中的uncertain函数和鲁棒优化模块求解两阶段鲁棒优化的子问题。
③.Yalmip工具箱中的鲁棒优化模块和常规的求解思路有什么异同。
④.使用KKT条件求解两阶段鲁棒优化的子问题,并使用C&CG算法进行迭代求解。
⑤.使用对偶变换求解两阶段鲁棒优化的子问题,并使用C&CG算法进行迭代求解。
⑥.采用Yalmip工具箱的内置函数,将线性约束写成紧凑矩阵形式的方法。
⑦.矩阵形式的两阶段鲁棒优化问题,如何快速写出子问题内层优化的KKT条件,并使用C&CG算法进行迭代求解。
⑧.矩阵形式的两阶段鲁棒优化问题,如何快速写出子问题内层优化的对偶问题,并使用C&CG算法进行迭代求解。
由于博客篇幅较长,将分上下两篇发布,其中上篇使用的是文献[1]中的算例,包含上述①-⑤的内容。下篇使用文献[2]中的算例,包含上述①、④、⑥-⑧的内容。
这篇博客是下篇的内容。
1.两阶段鲁棒优化基本形式
如文献[1]中所述,标准的两阶段鲁棒优化问题的形式为:

其中,y为第一阶段决策变量,u为不确定变量,x为第二阶段决策变量。和分析单阶段鲁棒优化问题的五个特征一样,拿到一个复杂的两阶段鲁棒优化问题先不用慌,按照下面的步骤进行分析即可:
1)确定第一阶段决策变量有哪些,将其与变量y对应。
2)确定第二阶段决策变量有哪些,将其与变量x对应。
3)确定不确定变量有哪些,将其与变量u对应。
4)确定优化问题中不确定集合的形式,并考虑是否可以直接使用Yalmip中的鲁棒优化模块进行求解。
5)确定目标函数是否有仅包含第一阶段决策变量的项,如果有的话可以单独拿出来。
6)确定子问题的目标函数,将其与鲁棒优化的标准形式相对应。
7)确定约束条件,考虑是否包含非线性约束,是否需要线性化。
8)求解max-min或者min-max类型的子问题。
9)使用迭代方式,将子问题产生的变量和约束不断添加到主问题中,最终得到最优解。
下面分别以文献[1]和[2]中的优化问题进行讲解说明:
2.两阶段鲁棒运输问题编程实战
更多内容,请关注Matlab+Yalmip两阶段鲁棒优化通用编程指南(上):
鲁棒优化入门(6)—Matlab+Yalmip两阶段鲁棒优化通用编程指南(上)
3.微电网两阶段鲁棒优化调度编程实战
第二个算例来源于文献[2],其两阶段鲁棒优化问题的形式为:
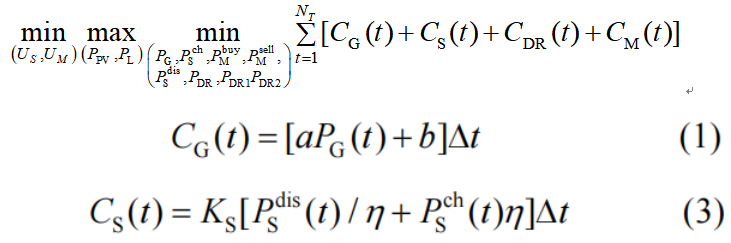
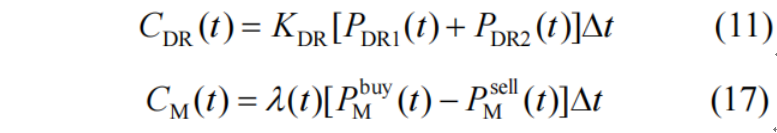
s.t.
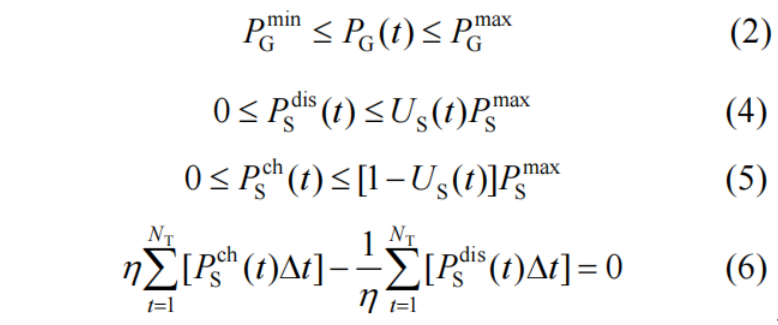
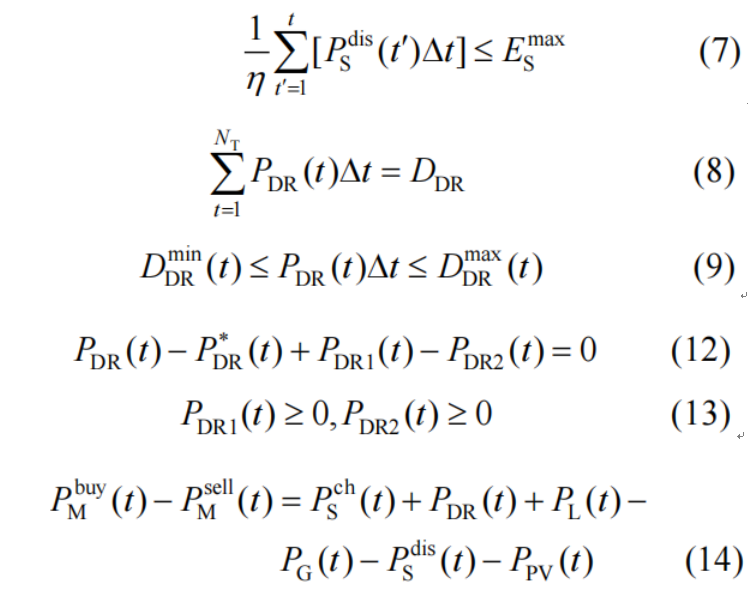
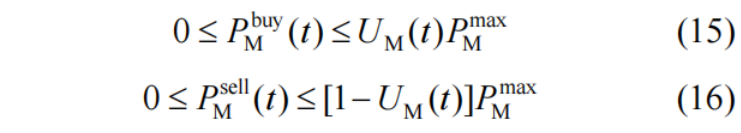
我之前写过一篇博客解析这篇论文,但是使用的是紧凑的矩阵形式。这次博客我先尝试使用一般形式的约束进行求解,方便大家体会采用矩阵形式求解两阶段鲁棒优化的方便之处。
首先逐步进行分析:
1)确定第一阶段决策变量有哪些。

2)确定第二阶段决策变量有哪些。

3)确定不确定变量有哪些。

4)确定优化问题中不确定集合的形式,并考虑是否可以直接使用Yalmip中的鲁棒优化模块进行求解。
该优化问题的不确定集中为箱式不确定集,但包含0-1变量,不可以直接使用Yalmip中的鲁棒优化模块进行求解。
5)确定目标函数是否有仅包含第一阶段决策变量的项,如果有的话可以单独拿出来。
该优化问题第一阶段和第二阶段目标函数相同。
6)确定子问题的目标函数,将其与两阶段鲁棒优化的标准形式相对应。
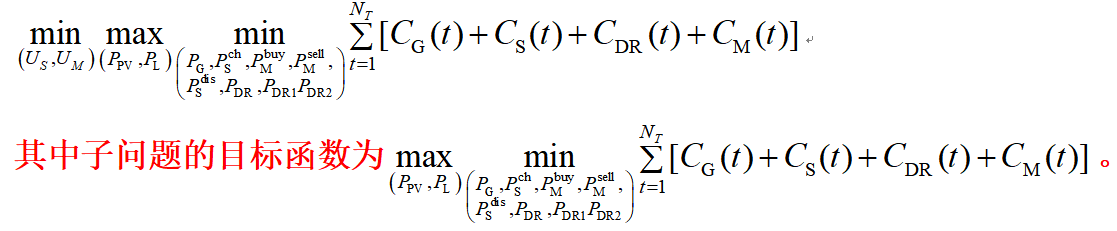
7)确定约束条件,考虑是否包含非线性约束,是否需要线性化。
子问题中的约束条件均为线性,但不确定变量的约束条件包含0-1变量,则含变量
的优化问题并不满足强对偶定理,KKT条件和对偶变换都无法适用。那是不是无法使用常规的方法求解单阶段鲁棒优化形式的子问题呢?
当然不是,如果出现这种情况,我们就可以把不确定变量写在外层。那么对于子问题的内层优化问题来说,变量是一个确定值,即使其中包含0-1变量,也只是一个常数。实际上子问题的内层优化并不包含0-1变量,因此还是可以使用常规的KKT条件或强对偶定理进行求解。但是由于不确定变量中包含0-1变量,直接通过uncertain函数直接使用Yalmip鲁棒优化模块的方法不可行。
分析完成后,分别使用KKT条件和强对偶定理求解子问题,具体如下:
3.1 KKT条件求解子问题
为了方便求解,我们首先把子问题的内层min优化问题写出来,并将所有约束写成≤0的形式或=0的形式:


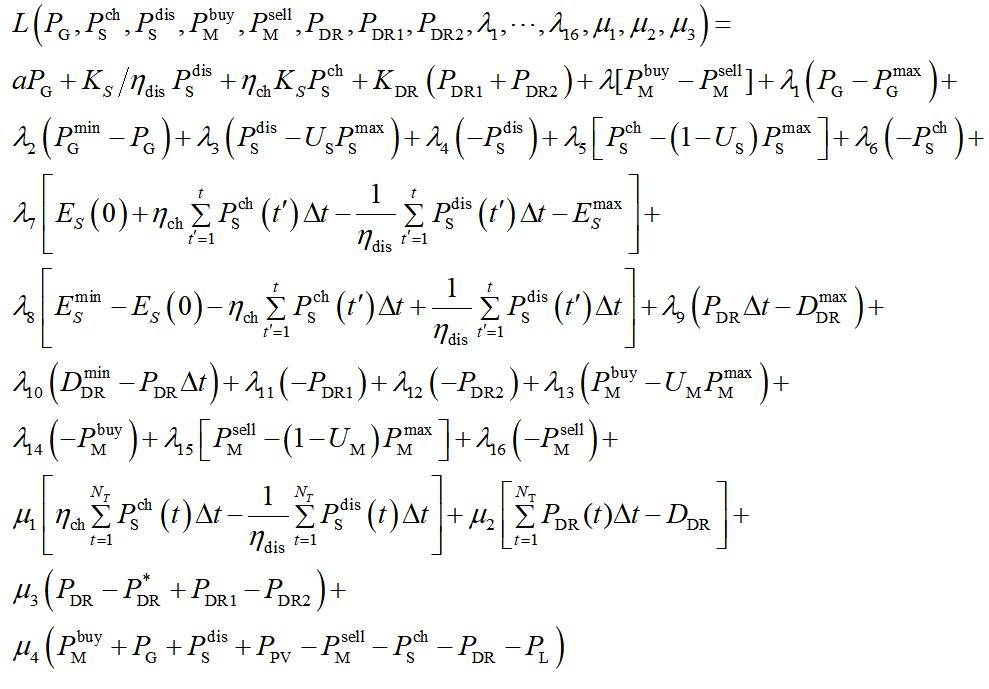
根据拉格朗日函数可以写出内层优化的KKT条件。
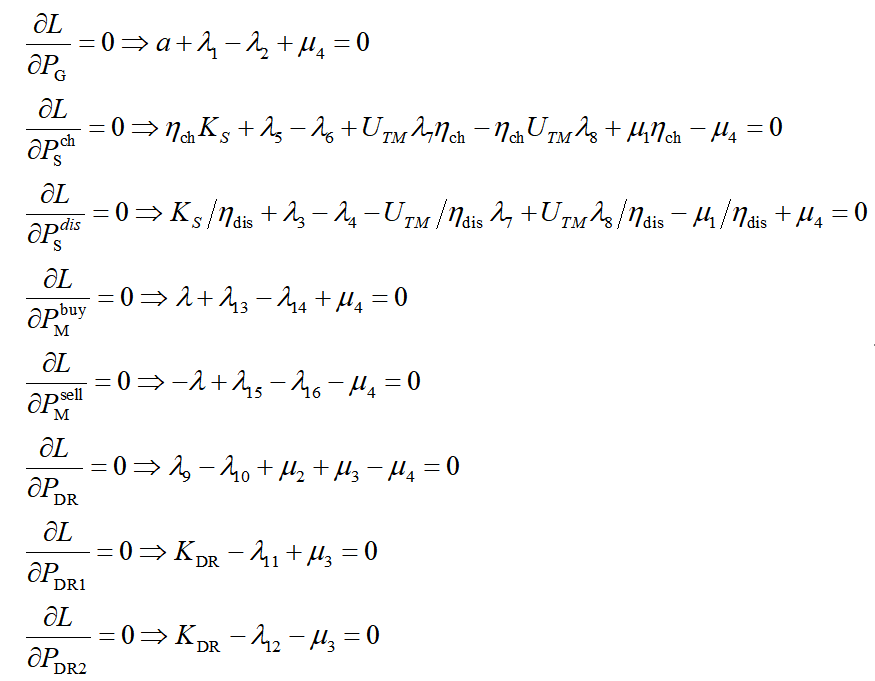
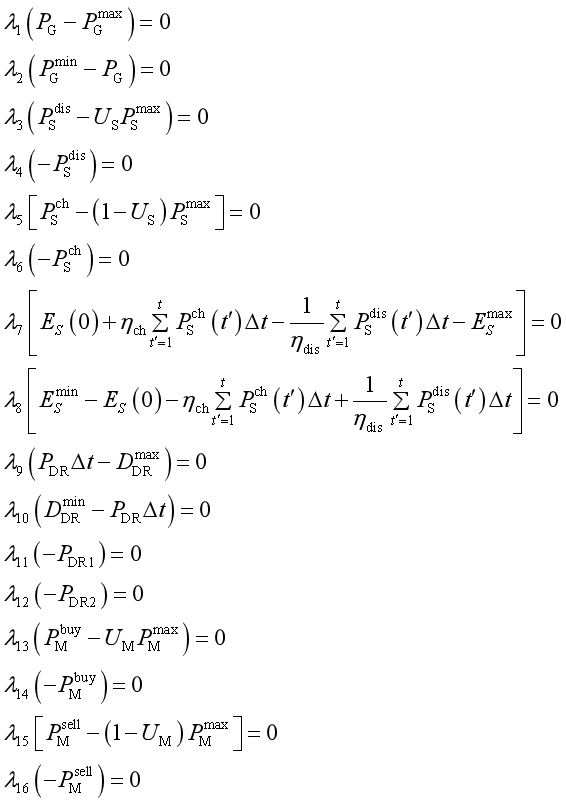
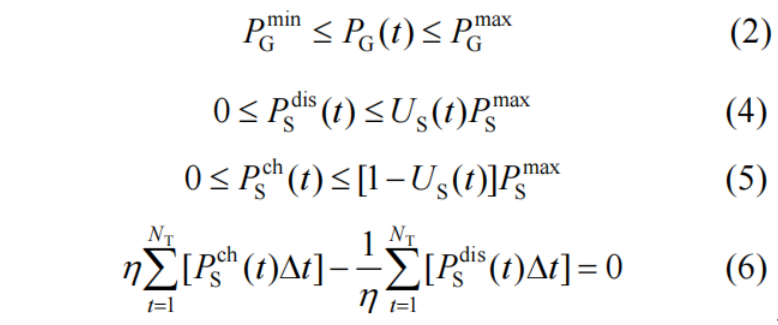
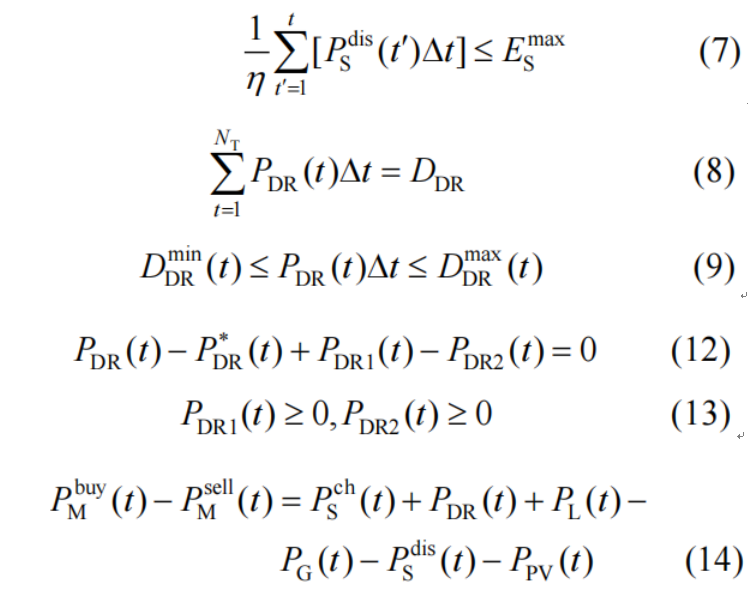
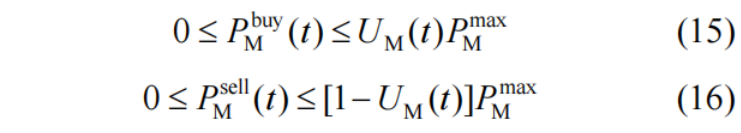
其中表示上三角全为1,主对角线以下全为0的24阶方阵,即:
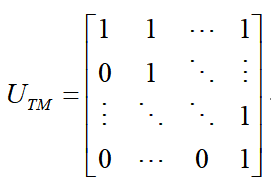
要想求解这个问题,还需要写出引入16组0-1变量,使用大M法将16组互补松弛条件转为线性约束,具体如下:
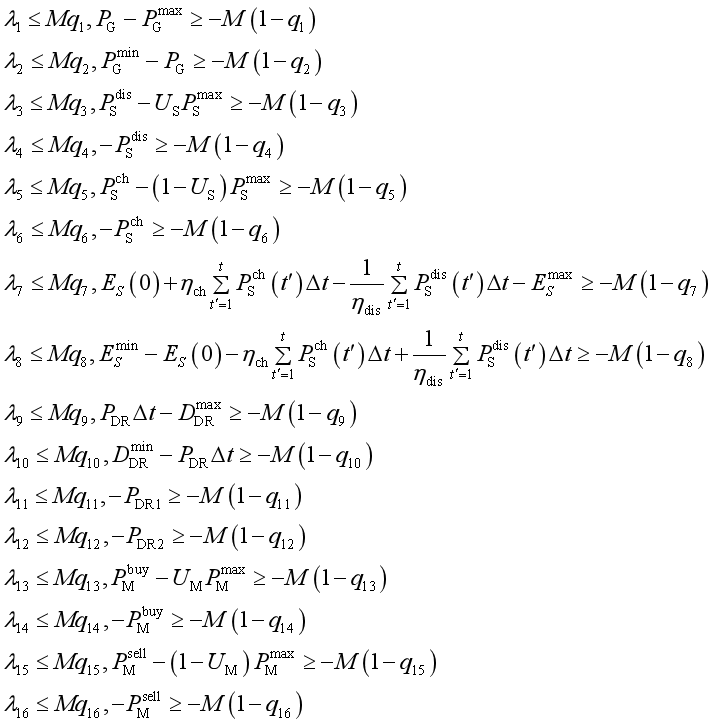
其中q1-q16都是0-1变量,qi和λi的维度相同。
将内层优化的KKT方程组添加到外层优化中,就可以将双层优化问题转为单层优化问题。经过上面的处理,便顺利将max-min形式的子问题转为混合整数线性规划问题,并可以使用Yalmip进行求解,代码在压缩包中的Problem2文件夹中,运行Problem2_subproblem_KKT1.m文件即可得到结果。
PS:假设第一阶段变量的取值:
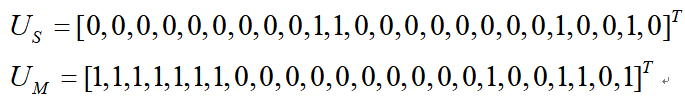
运行结果如下:
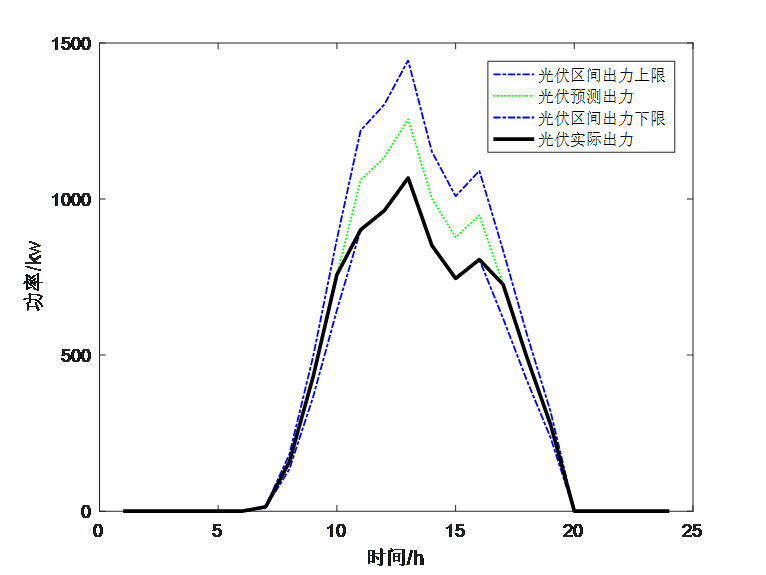
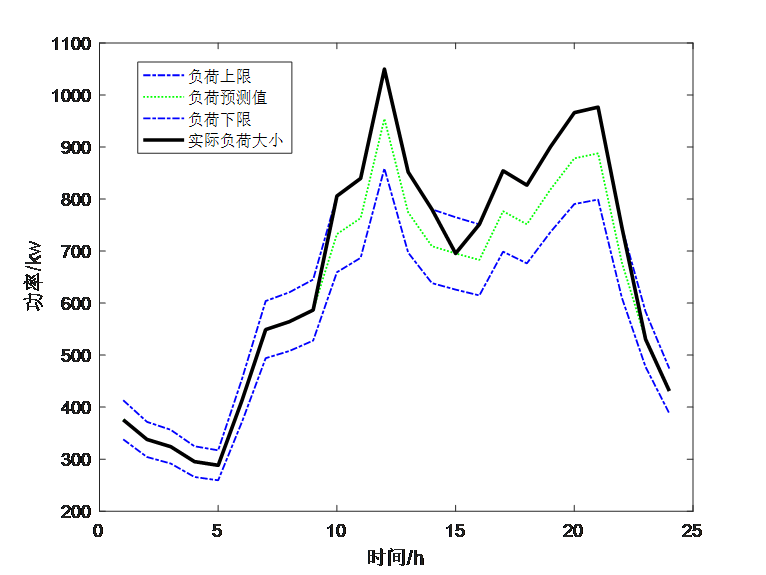
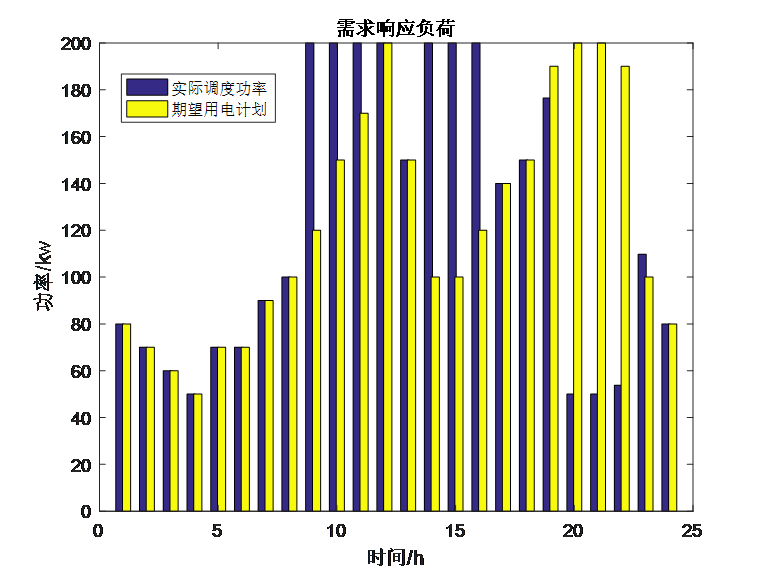

从运行结果可以看出,使用KKT条件可以正常求出最优解,但由于引入了非常多的拉格朗日乘子和相应的0-1变量,对于初始的约束形式手动写KKT条件非常麻烦,一旦出错也很难发现问题在哪。
3.2 将两阶段鲁棒优化问题写成矩阵形式
对于约束条件比较复杂的两阶段鲁棒优化问题,先把目标函数和约束条件写成紧凑的矩阵形式再使用KKT条件或对偶变换求解会方便很多。文献[1]中将优化问题写成了紧凑的矩阵形式,但存在一定问题,我在此重新梳理一遍。
首先,将优化问题写成紧凑的矩阵形式(等式约束都改写成不等式形式,例如x=0可以写成x≥0,-x≥0):
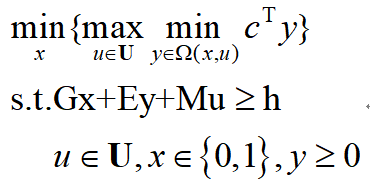
其中,第一阶段决策变量x是一个48维的列向量:
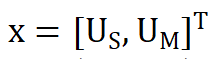
第二阶段决策变量y是一个192维的列向量:
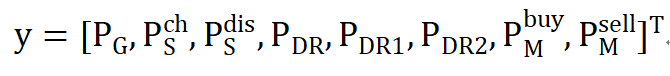
c和y的维度一样,但c是一个192维的常数列向量:
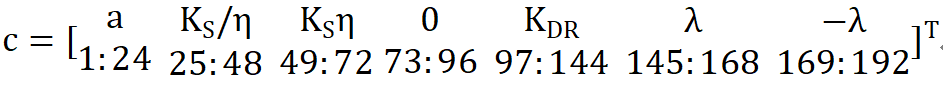
那么如何确定矩阵G,矩阵E,矩阵M,向量h的取值呢?之前的博客中我采用了手动推导的方式(微电网两阶段鲁棒优化经济调度方法matlab代码_)。
这次我来教大家使用Yalmip工具箱中的函数depends、getbase、getbasematrix、see写出约束矩阵取值的方法,函数的语法可以参考官方文档。
下面是一个简单的线性规划问题:

我用这个例子来帮助大家体会depends、getbase、getbasematrix、see等函数的用法,代码如下:
clc
clear
close all
warning off
yalmip('clear')%% 决策变量
sdpvar x1 x2
%% 目标函数
obj = x1 + 2*x2;z = [-2*x1 + 3*x2 - 12 ;x1 + x2 - 14;-3*x1 + x2 + 3;3*x1 + x2 - 30];x1_index = depends(x1)
x2_index = depends(x2)
M1 = full(getbase(z))
M2 = full(getbasematrix(z,depends(x1)))
M3 = full(getbasematrix(z,depends(x2)))
see(z)运行结果如下:
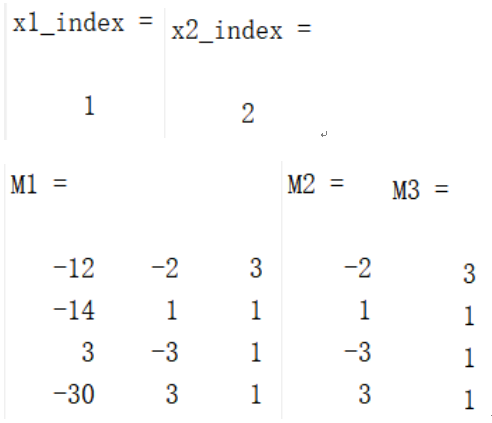
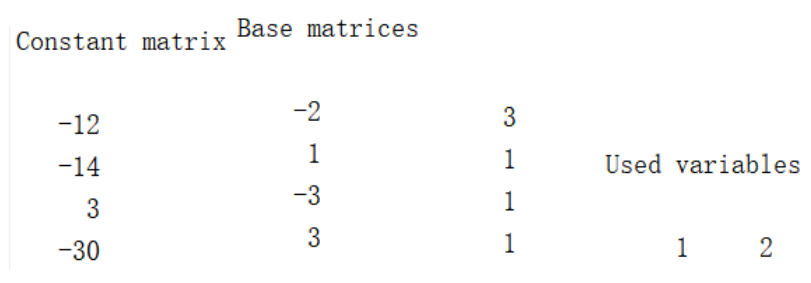
观察可知,depends函数返回的是变量在Yalmip工具箱中的编号,getbase函数以稀疏矩阵的形式返回sdpvar变量中的常数项系数以及变量系数,getbasematrix函数以稀疏矩阵的形式返回sdpvar变量中指定编号的变量系数,see函数直接在命令行输出sdpvar变量中的常数项、变量系数以及用到的变量编号。
假设我们想把上面的优化问题写成紧凑的矩阵形式:
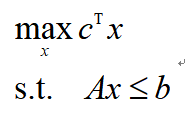
求矩阵A、b、c,然后使用矩阵形式求解优化问题的代码如下:
clc
clear
close all
warning off
yalmip('clear')%% 决策变量
sdpvar x1 x2%% 求系数矩阵
obj0 = x1 + 2*x2;z = [-2*x1 + 3*x2 - 12 ;x1 + x2 - 14;-3*x1 + x2 + 3;3*x1 + x2 - 30];M1 = full(getbase(z));
M2 = full(getbase(obj0));
index = depends([x1 x2]);
A = M1(:,index + 1);
b = -M1(:,1);
c = M2(index + 1)';%% 矩阵形式的目标函数
x = [x1;x2];
obj = c'*x;
C = [A*x <= b , x >= 0];%% 求解优化问题
ops = sdpsettings('verbose', 3, 'solver', 'gurobi');
sol = optimize(C , -obj ,ops);%% 判断求解是否成功
if sol.problem == 0disp('求解成功!!!');x = value(x)
elsedisp(['求解失败,原因为',sol.info]);
end运行结果如下:
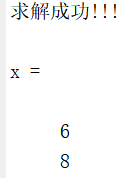
采用相同的方法,将文献[1]所提确定性优化问题改写成矩阵形式求解的代码在压缩包中的Problem2文件夹中,运行Problem2_matrix.m文件即可得到结果。

3.3 矩阵形式的C&CG算法与KKT条件求解
原始子问题为:
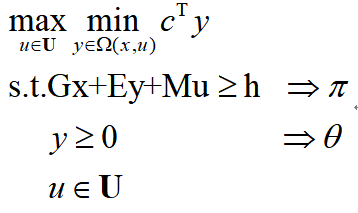
内层优化中变量x和不确定变量u都可以看作常数,其拉格朗日函数可以写作:
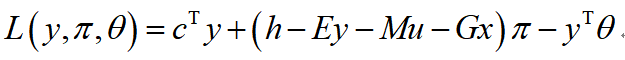
其中,π和θ都是拉格朗日乘子。根据拉格朗日函数进一步写出KKT条件:
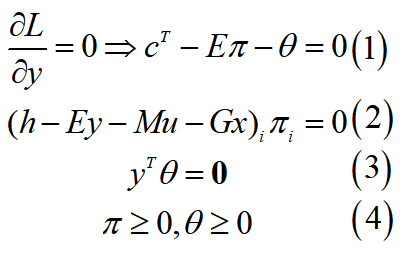
这就是初始的KKT条件,可以进一步化简。首先根据式(1)和(4)可以得到:
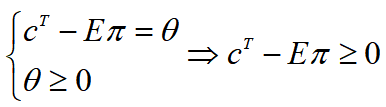
然后,根据式(1)和(3)可以得到:
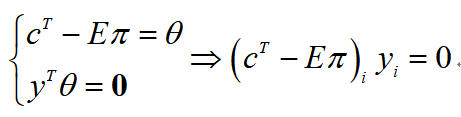
经过这样处理,就可以消去变量θ,减少决策变量的数目,得到:
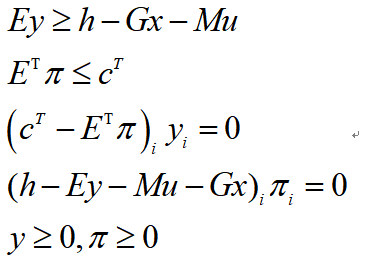
其中包含两项互补松弛条件,可以通过引入0-1变量,使用大M法转换为线性约束:
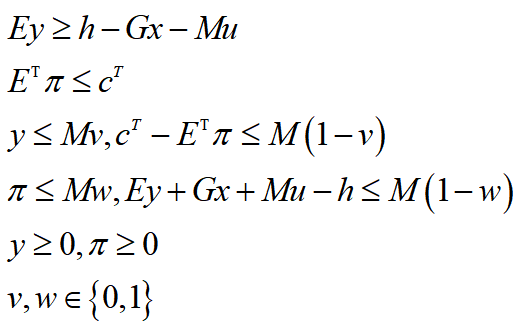
将KKT条件添加到子问题的外层优化中,子问题便转为:
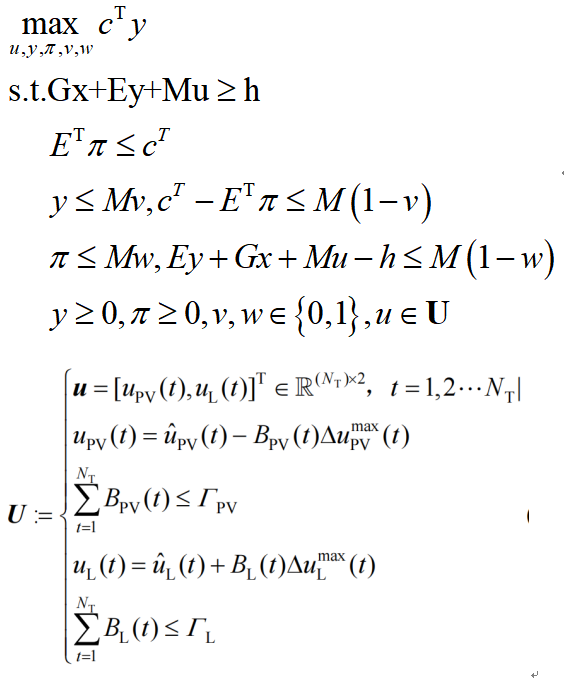
子问题变成了一个混合整数线性规划,可以采用求解器有效地进行求解。
再复习一下,我们把文献[2]中所提两阶段鲁棒优化分解成一个主问题MP2_KKT和一个子问题SP2_KKT:
主问题MP2_KKT:
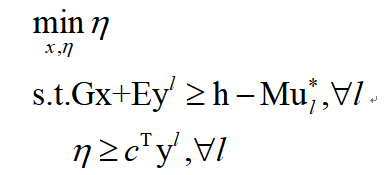

子问题SP2_KKT:
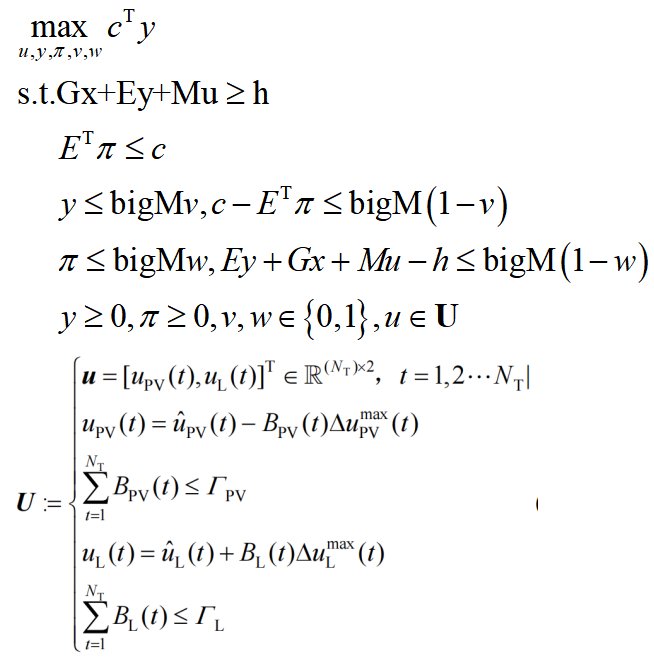


使用KKT条件+C&CG算法求解该两阶段鲁棒优化问题的代码在压缩包中的Problem2文件夹中,运行Problem2_KKT.m文件即可得到结果。
3.4 矩阵形式的C&CG算法与对偶变换求解
原始子问题为:
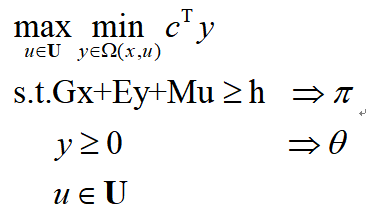
其内层优化min问题的对偶问题可以写做:
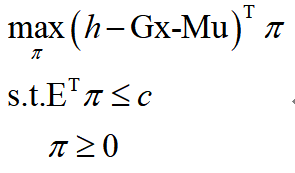
将其与外层max问题合并得到:

该问题的目标函数中包含的非线性项,可以进行线性化,也可以直接使用求解器进行求解。为了方便起见,我直接使用了求解器进行求解。但是由于问题规模比较大,求解时间会比较长(大概要3小时左右才能得到最优解)。
首先,将不确定变量u写成:
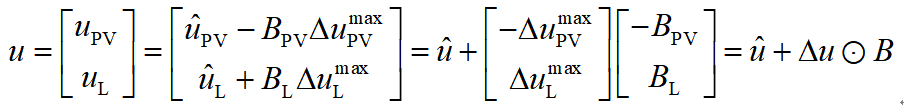
式中,符号表示矩阵的Hadamard乘积(哈达玛积 Hadamard Product - 知乎),即对应元素相乘,对应于matlab中的“.*”符号。在此基础上,可以对原优化问题的目标函数进行化简:
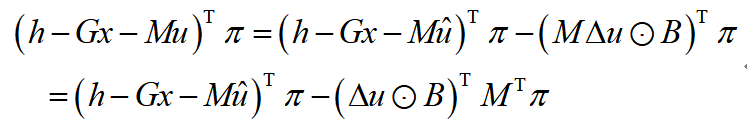
两阶段鲁棒优化问题可以分为主问题和子问题:
对偶变换版本主问题MP2_dual:
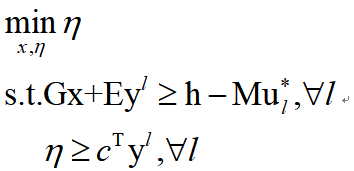
对偶变换版本子问题SP2_dual:
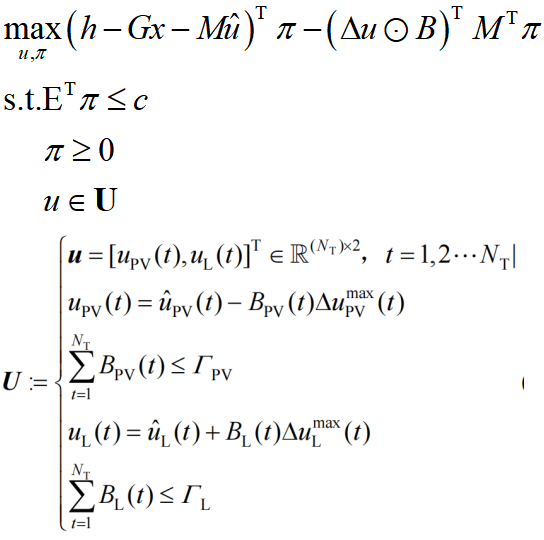
使用C&CG算法与对偶变换求解两阶段鲁棒优化的步骤概括如下:


使用对偶变换+C&CG算法求解该两阶段鲁棒优化问题的代码在压缩包中的Problem2文件夹中,运行Problem2_dual.m文件即可得到结果。
参考文献:
[1]Zeng B, Zhao L. Solving two-stage robust optimization problems using a column-and-constraint generation method[J]. Operations Research Letters, 2013, 41(5): 457-461.
[2]刘一欣,郭力,王成山.微电网两阶段鲁棒优化经济调度方法[J].中国电机工程学报,2018,38(14):4013-4022+4307.
PS:
完整资料可以私信博主获取。
相关文章:

鲁棒优化入门(7)—Matlab+Yalmip两阶段鲁棒优化通用编程指南(下)
0.引言 上一篇博客介绍了使用Yalmip工具箱求解单阶段鲁棒优化的方法。这篇文章将和大家一起继续研究如何使用Yalmip工具箱求解两阶段鲁棒优化(默认看到这篇博客时已经有一定的基础了,如果没有可以看看我专栏里的其他文章)。关于两阶段鲁棒优化与列与约束生成算法的原…...
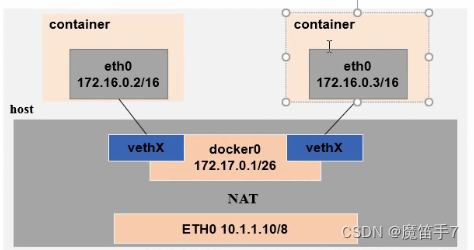
Docker技术--Docker中的网络问题
1.docker中的网络通信 如果想要弄清楚docker中的网络通信问题,其实需要弄清楚这几个问题就可以:容器与容器之间的通信、容器与外部网络之间的通信、外部网络与容器之间的通信。 -a:容器与容器之间的通信,如下所示: 在默认情况下,docker使用网桥(Bridge模式)与NAT通信。这…...

ASP.NET Core 中的两种 Web API
ASP.NET Core 有两种创建 RESTful Web API 的方式: 基于 Controller,使用完整的基于ControllerBase的基类定义接口endpoints。基于 Minimal APIs,使用Lambda表达式定义接口 endpoints。 基于 Controller 的 Web API 可以使用构造函数注入&a…...
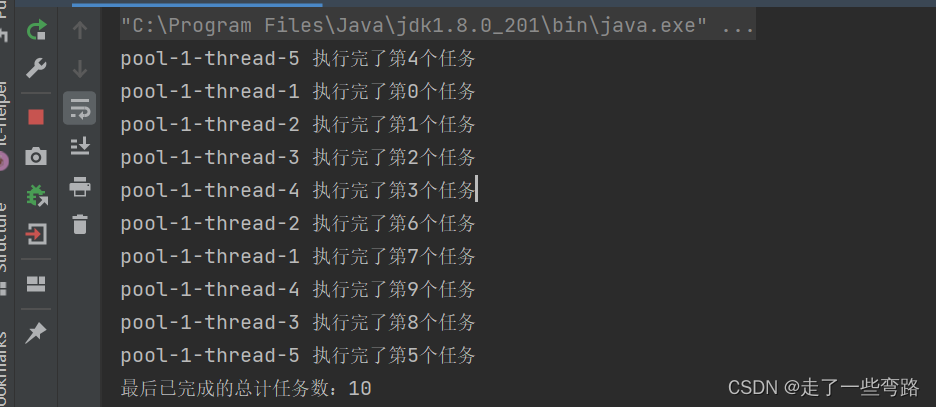
【线程池】如何判断线程池中的任务执行完毕(三)
目录 前言 1. isTerminated()方法 2. awaitTermination()方法 3.getTaskCount()方法和executor.getCompletedTaskCount()方法结合使用 4.使用CountDownlatch类 前言 通常我们使用线程池的时候,系统处于运行的状态,而线程池本身就是主要为了线程复用&…...

Qt/C++编写视频监控系统81-Onvif报警抓图和录像并回放
一、前言 视频监控系统中的图文警情模块,是通过Onvif协议的事件订阅拿到的,通过事件订阅后,设备的各种报警事件比如入侵报警/遮挡报警/越界报警/开关量报警等,触发后都会主动往订阅者发送,而且一般都是会发送两次&…...

浅谈安防视频监控平台EasyCVR视频汇聚平台对于夏季可视化智能溺水安全告警平台的重要性
每年夏天都是溺水事故高发的时期,许多未成年人喜欢在有水源的地方嬉戏,这导致了悲剧的发生。常见的溺水事故发生地包括水库、水坑、池塘、河流、溪边和海边等场所。 为了加强溺水风险的提示和预警,完善各类安全防护设施,并及时发现…...
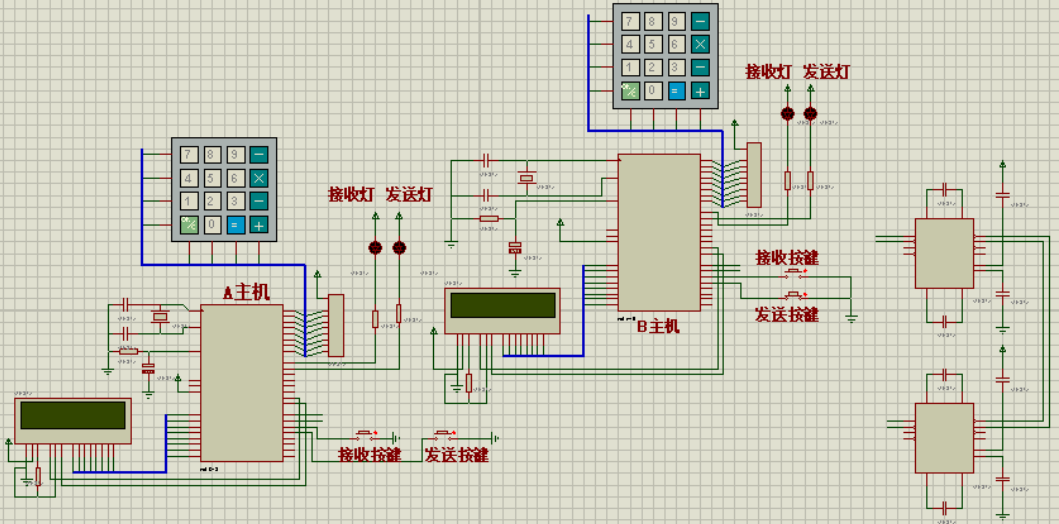
基于单片机的串行通信发射机设计
一、项目介绍 串行通信是一种常见的数据传输方式,允许将数据以比特流的形式在发送端和接收端之间传输。当前实现基于STC89C52单片机的串行通信发射机,通过红外发射管和接收头实现自定义协议的数据无线传输。 二、系统设计 2.1 单片机选择 在本设计中&…...

MySQL数据库——多表查询(3)-自连接、联合查询、子查询
目录 自连接 查询语法 自连接演示 联合查询 查询语法 子查询 介绍 标量子查询 列子查询 行子查询 表子查询 自连接 通过前面的学习,我们对于连接已经有了一定的理解。而自连接,通俗地去理解就是自己连接自己,即一张表查询多次。…...

day53 动规.p14 子序列
- 1143.最长公共子序列 cpp class Solution { public: int longestCommonSubsequence(string text1, string text2) { vector<vector<int>> dp(text1.size() 1, vector<int>(text2.size() 1, 0)); for (int i 1; i < text1.size(…...

将docker打包成镜像并保存到本地
如果想重装系统,又不想破坏docker里面配好的环境,那么可以将docker镜像打包到本地进行保存。 1. 将docker打包成镜像 命令:docker commit 容器id 镜像名:tag 使用docker ps -a即可查看容器相关信息 docker commit dd25c7c6bf17 zm_cu101:c…...

Harmony数据存储工具类
使用的是mmkv 1、安装mmkv ohpm install @ohos/mmkv2、封装 import{MMKV, SerializeBase} from @ohos/mmkv/*** 数据存储工具类*/ class MMKVUtil{private filePath:string = private cachePath:string = private mmkv:MMKVprivate mmapID:string="MMKV"construct…...
ROS 2官方文档(基于humble版本)学习笔记(一)
ROS 2官方文档(基于humble版本)学习笔记(一) 一、安装ROS 2二、按教程学习1.CLI 工具配置环境使用turtlesim,ros2和rqt安装 turtlesim启动 turtlesim使用 turtlesim安装 rqt使用 rqt重映射关闭turtlesim 由于市面上专门…...
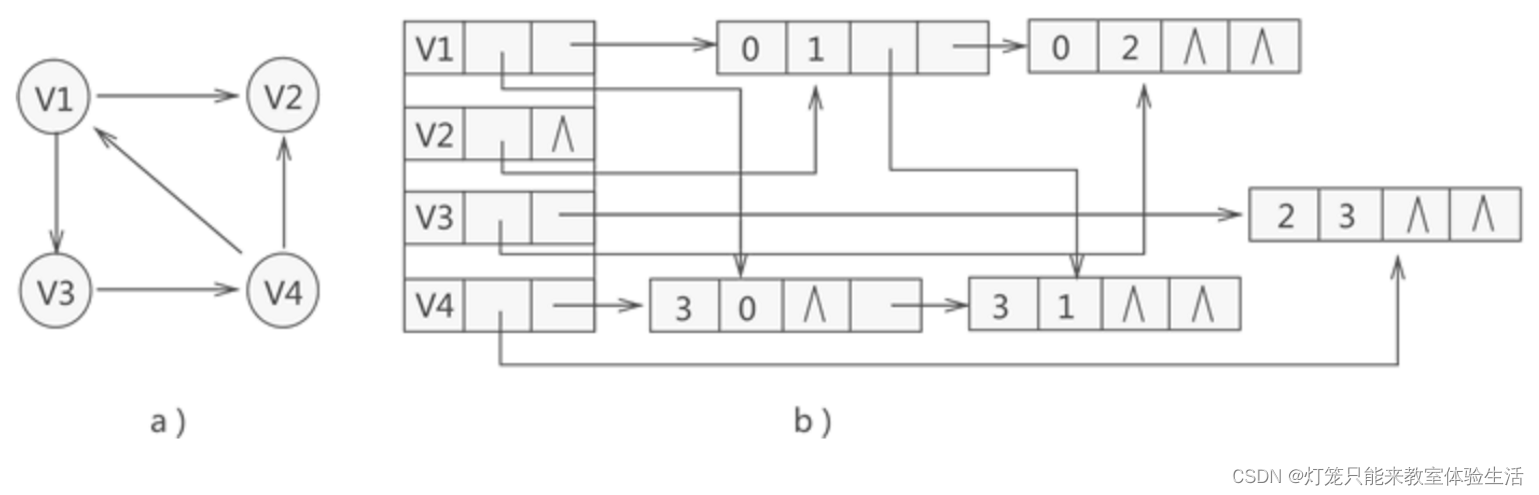
【数据结构】十字链表的画法
十字链表的基本概念 有向边又称为弧 假设顶点 v 指向 w,那么 w 称为弧头,v 称为弧尾 顶点节点采用顺序存储 顶点节点 data:存放顶点的信息firstin:指向以该节点为终点(弧头)的弧节点firstout࿱…...
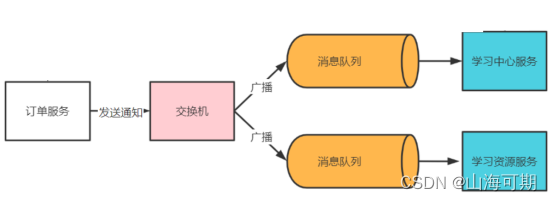
使用rabbitmq进行支付之后的消息通知
订单服务完成支付后将支付结果发给每一个与订单服务对接的微服务,订单服务将消息发给交换机,由交换机广播消息,每个订阅消息的微服务都可以接收到支付结果. 微服务收到支付结果根据订单的类型去更新自己的业务数据。 相关技术方案 使用消息…...

【100天精通python】Day47:python网络编程_Web开发:web服务器,前端基础以及静态服务器
目录 1 网络编程与web编程 1.1 网络编程 1.2 web编程 1.3 前后端交互的基本原理 2 Web开发基础 2.1 HTTP协议 2.2 Web服务器 2.3 前端基础 2.3.1 HTML(超文本标记语言) 2. 3.2 CSS(层叠样式表) 2.3.3 JavaScript 2.…...

Web框架Beego
beego简介第一个beego项目beego项目结构分析bee 工具简介beego参数配置beego路由设置beego控制器介绍beego获取参数beego ORMbeego orm高级查询beego 原生sql查询beego 模板语法指南beego模板处理...
Kubernetes(K8s)基本环境部署
此处只做学习使用,配置单master环境。 一、环境准备 1、ip主机规划(准备五台新机)>修改各个节点的主机名 注意:关闭防火墙与selinux 节点主机名ip身份joshua1 kubernetes-master.openlab.cn 192.168.134.151masterjoshua2k…...
antd5:form组件底层封装库field-form-1.37.0启动
一开始node版本是18.16.0 npm install发现安装依赖成功 npm start发现启动出错 node:internal/crypto/hash:71this[kHandle] new _Hash(algorithm, xofLen);^Error: error:0308010C:digital envelope routines::unsupportedat new Hash (node:internal/crypto/hash:71:19)…...
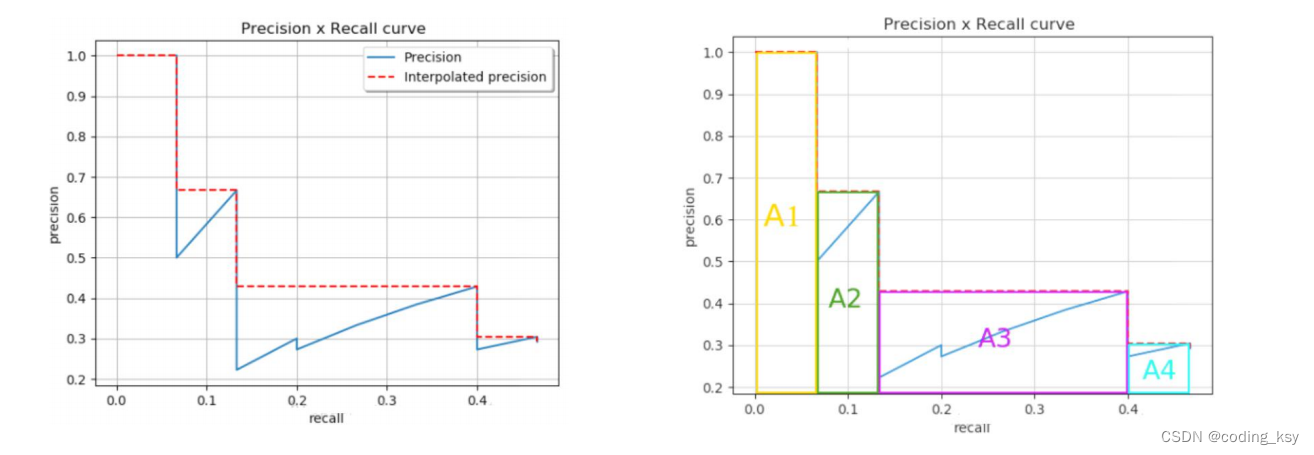
深度学习经典检测方法的概述
深度学习经典的检测方法 two-stage(两阶段):Faster-rcnn Mask-Rcnn系列 两阶段(two-stage)是指先通过一个区域提取网络(region proposal network,RPN)生成候选框,再通过…...

viewpager2导致的mViews下标越界问题
viewpager2种在嵌套一个RecyclerView场景:左右滑动,上下滑动,出现mViews为null问题。 //RecyclerView布局为 new StaggeredGridLayoutManager(2,StaggeredGridLayoutManager.VERTICAL) 由于使用viewpager2导致布局缓存的销毁,会…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

二维FDTD算法仿真
二维FDTD算法仿真,并带完全匹配层,输入波形为高斯波、平面波 FDTD_二维/FDTD.zip , 6075 FDTD_二维/FDTD_31.m , 1029 FDTD_二维/FDTD_32.m , 2806 FDTD_二维/FDTD_33.m , 3782 FDTD_二维/FDTD_34.m , 4182 FDTD_二维/FDTD_35.m , 4793...
