优思学院|六西格玛中的概率分布有哪些?

为什么概率分布重要?
概率分布是统计学中一个重要的概念,它帮助我们理解随机变量的分布情况以及与之相关的概率。在面对具体问题时,了解概率分布可以帮助我们选择适当的检验或分析策略,以解决问题并做出合理的决策。
常见的概率分布
正态分布、韦伯分布和对数正态分布
连续变量的总体可以展现为不同的基础分布,常见的有正态分布、韦伯分布和对数正态分布等。这些分布在不同情境下具有不同的应用。正态分布通常在均值分析中应用较多,而韦伯分布和对数正态分布则更适合描述其他类型的概率特征。
抽样分布与总体分布
抽样分布是描述样本统计量的分布,通过对总体进行取样来获得。抽样分布可以帮助我们推断总体特征,并进行统计推断。理解抽样分布对于有效地从样本中推断总体的特征至关重要。
正态分布与均值分析
正态分布在统计学中扮演着重要的角色。尤其在均值分析时,我们通常不需要考虑总体的具体分布情况,因为根据中心极限定理,样本均值的取样分布趋向于正态分布。然而,在某些情况下,对总体的分布有更深入的理解是必要的,特别是当我们需要更多关于总体比例的信息时。
韦伯分布和对数正态分布的应用
有时候,用正态分布可能无法准确描述连续响应数据的概率特征。在这种情况下,韦伯分布或对数正态分布可能更适用。这两种分布可以更好地解释总体的概率特征,有助于我们更好地理解问题并做出准确的分析。
其他常见分布类型
二项分布、泊松分布和超几何分布
除了连续变量,离散变量的分布也是研究的重点。二项分布是描述一系列独立重复实验的结果的概率分布,适用于类似抛硬币、掷骰子等情况。超几何分布与二项分布类似,但应用于样本较大的情况。
泊松分布则适用于描述在固定时间或空间内随机事件发生次数的概率分布。这些分布在实际问题中有广泛的应用,帮助我们理解离散事件的概率分布情况。
结论
概率分布是统计学中不可或缺的概念,它指导着我们如何理解随机变量的分布情况,并在实际问题中做出决策。了解不同类型的概率分布以及它们的应用场景,有助于我们更好地分析问题,做出准确的预测。
常见问题解答
什么是概率分布?
概率分布是用来描述随机变量可能取值及其概率的函数,帮助我们理解变量的分布情况。
为什么正态分布重要?
正态分布在统计学中广泛应用,因为它在许多实际问题中都能准确地描述数据分布情况。
韦伯分布和对数正态分布有什么区别?
韦伯分布适用于描述不同于正态分布的概率特征,而对数正态分布则适用于对数转换后呈正态分布的数据。
什么是抽样分布?
抽样分布是样本统计量的分布,通过从总体中抽取样本来获得,用于做出总体特征的推断。
离散变量的常见分布是什么?
离散变量的常见分布包括二项分布、泊松分布和超几何分布,它们适用于不同类型的离散事件。
相关文章:

优思学院|六西格玛中的概率分布有哪些?
为什么概率分布重要? 概率分布是统计学中一个重要的概念,它帮助我们理解随机变量的分布情况以及与之相关的概率。在面对具体问题时,了解概率分布可以帮助我们选择适当的检验或分析策略,以解决问题并做出合理的决策。 常见的概率…...
工控上位机程序为什么只能用C语言?
工控上位机程序并不只能用C#开发,实际上在工业自动化领域中,常见的上位机开发语言包括但不限于以下几种:C#: C#是一种常用的编程语言,在工控领域中被广泛使用。它具有良好的面向对象特性和丰富的类库支持,可以实现高性…...
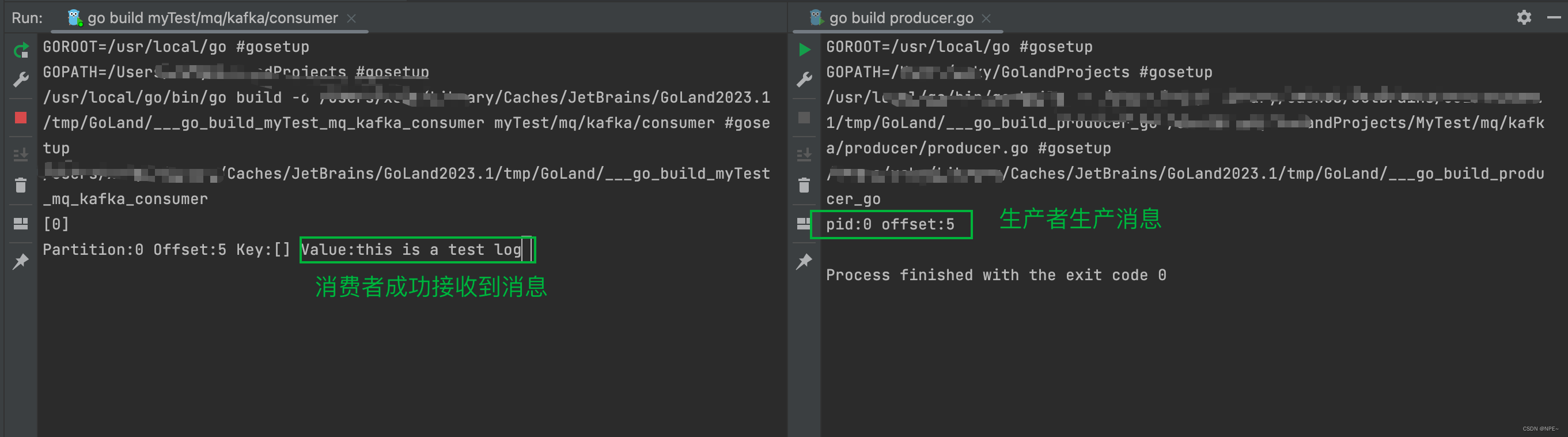
Go操作各大消息队列教程(RabbitMQ、Kafka)
Go操作各大消息队列教程 1 RabbitMQ 1.1 概念 ①基本名词 当前市面上mq的产品很多,比如RabbitMQ、Kafka、ActiveMQ、ZeroMQ和阿里巴巴捐献给Apache的RocketMQ。甚至连redis这种NoSQL都支持MQ的功能。 Broker:表示消息队列服务实体Virtual Host&#x…...

对话出海企业:2023亚马逊云科技出海日圆桌论坛
在全球经济亟待复苏的今天,持续对外开放是中国未来经济发展重要的“两条腿”之一。在愈发饱和的国内市场,中国企业需要对外寻找全新机遇才能在未来不确定的市场博弈下生存下去。“出海”,也成为近几年最炙手可热的词汇之一,大量中…...

【图解算法数据结构】分治算法篇 + Java代码实现
文章目录 一、重建二叉树二、数值的整数次方三、打印从 1 到最大的 n 位数四、二叉搜索树的后序遍历序列五、数组中的逆序对 一、重建二叉树 public class Solution {int[] preorder;HashMap<Integer, Integer> dic new HashMap<>();public TreeNode buildTree(in…...
——Ubuntu开机自动执行命令)
Ubuntu系统环境搭建(八)——Ubuntu开机自动执行命令
ubuntu环境搭建专栏🔗点击跳转 Ubuntu系统环境搭建(八)——Ubuntu开机自动执行命令 修改文件 vim /etc/rc.local以自启动mysql为例,在文件末尾添加 /usr/local/mysql8/bin/mysqld_safe --defaults-file/usr/local/etc/my.cnf …...
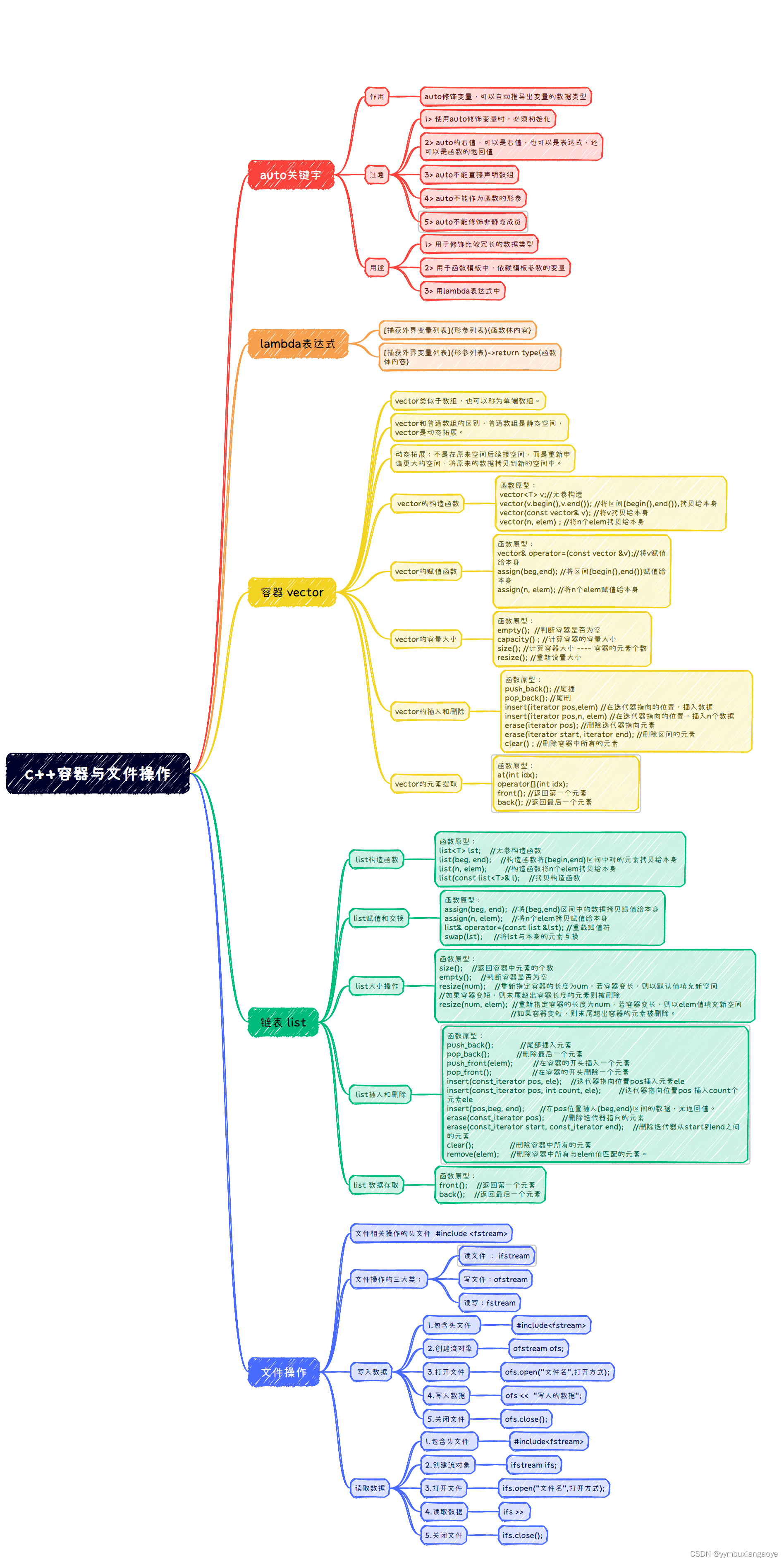
c++(8.29)auto关键字,lambda表达式,数据类型转换,标准模板库,list,文件操作+Xmind
作业: 封装一个学生的类,定义一个学生这样类的vector容器, 里面存放学生对象(至少3个) 再把该容器中的对象,保存到文件中。 再把这些学生从文件中读取出来,放入另一个容器中并且遍历输出该容器里的学生。…...
)
Docker学习笔记(持续更新)
Docker学习目录 1.基础1.1 Docker简介1.1.1 Why Docker?1.1.2 Docker理念1.1.3 容器与虚拟机1.1.4 Docker能做什么? 1.2 Docker的基本组成1.2.1 Docker的三要素1.2.2 Docker平台架构 1.基础 1.1 Docker简介 1.1.1 Why Docker? 在个人笔记本…...

无涯教程-Android - 应用组件
应用程序组件是Android应用程序的基本组成部分,这些组件需要在应用程序清单文件 AndroidManifest.xml 注册,该文件描述了应用程序的每个组件以及它们如何交互。 Android应用程序可以使用以下四个主要组件- Sr.NoComponents & 描述1 Activities 它们…...
树与图c++
1.树 前言 本文主要介绍的数据结构之树型结构的相关知识,树型数据结构是面试官面试的时候非常喜欢考的一种数据结构,树形结构的遍历也是大厂笔试非常喜欢设置的考点,这些内容都会在本篇文章中进行详细的介绍,并且还会介绍一些常…...
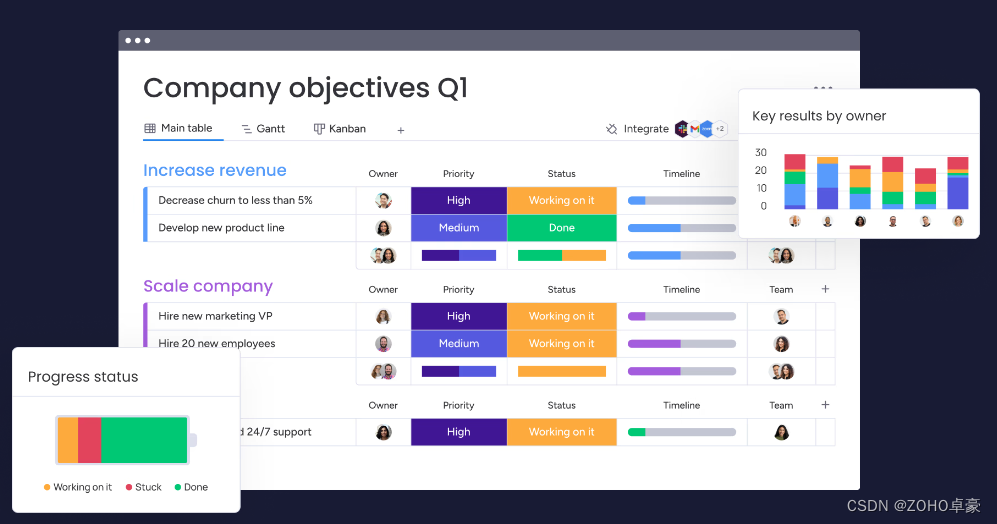
中小企业常用的 IT 项目管理软件有哪些?
越热门,越贵的IT项目管理软件越好用吗?对于预算有限的中小型企业来说,如何选择一款适合自己的项目管理工具着实是个头疼的问题。 首先适用于中小型企业使用的 IT 项目管理软件需要具备哪些特点呢? 1、简单易用:中小企…...

汇编原理计算方法:物理地址=段地址*16+偏移地址
文章目录 计算方法计算错误分析 计算方法 根据进制的不同选择不同的计算方法 注意:物理地址、段地址和偏移地址的进制统一,要么都是二进制,要么都是十六进制,一般而言多是十六进制 若是二进制表达,则将段地址左移四…...
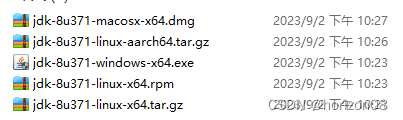
jdk-8u371-linux-x64.tar.gz jdk-8u371-windows-x64.exe 【jdk-8u371】 全平台下载
jdk-8u371 全平台下载 jdk-8u371-windows-x64.exejdk-8u371-linux-x64.rpmjdk-8u371-linux-x64.tar.gzjdk-8u371-macosx-x64.dmgjdk-8u371-linux-aarch64.tar.gz 下载地址 迅雷云盘 链接:https://pan.xunlei.com/s/VNdLL3FtCnh45nIBHulh_MDjA1?pwdw4s6 百度…...
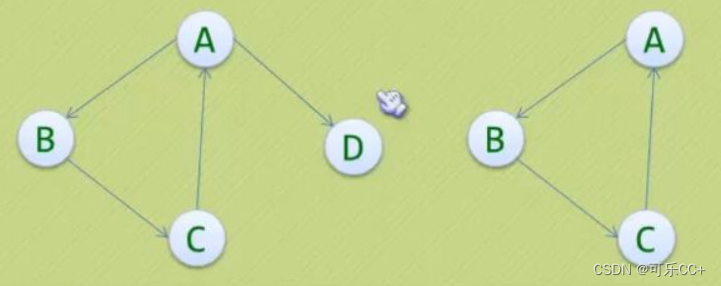
数据结构体--5.0图
目录 一、定义 二、图的顶点与边之间的关系 三、图的顶点与边之间的关系 四、连通图 五、连通图的生成树定义 一、定义 图(Graph)是由顶点的又穷非空集合合顶点之间边的集合组成,通常表示为:G(V,E&…...

深入剖析 Golang 程序启动原理 - 从 ELF 入口点到GMP初始化到执行 main!
大家好,我是飞哥! 在过去的开发工作中,大家都是通过创建进程或者线程来工作的。Linux进程是如何创建出来的? 、聊聊Linux中线程和进程的联系与区别! 和你的新进程是如何被内核调度执行到的? 这几篇文章就是…...
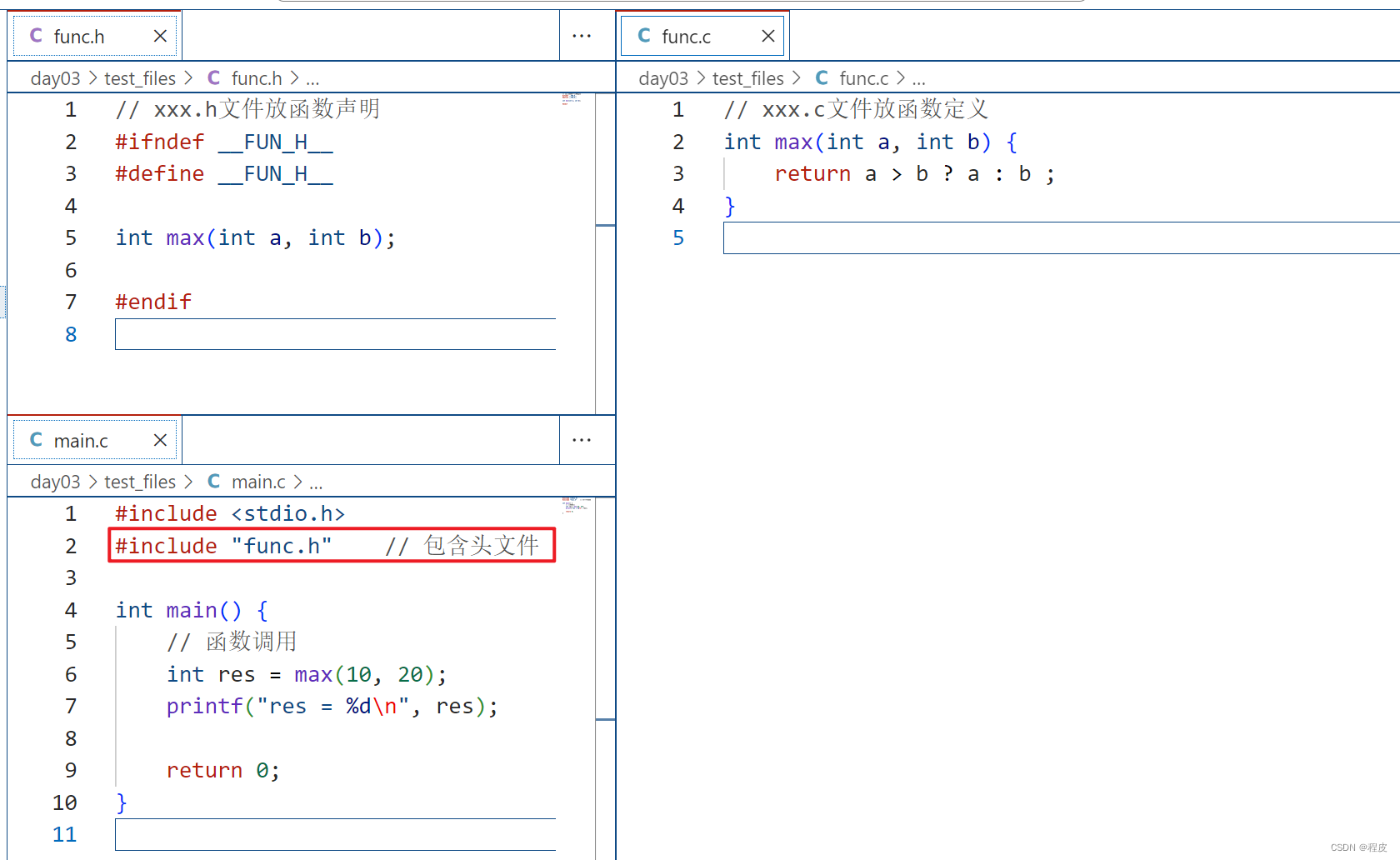
C语言——多文件编程
多文件编程 把函数声明放在头文件xxx.h中,在主函数中包含相应头文件在头文件对应的xxx.c中实现xxx.h声明的函数 防止头文件重复包含 当一个项目比较大时,往往都是分文件,这时候有可能不小心把同一个头文件 include 多次,或者头…...

Git学习part1
02.尚硅谷_Git&GitHub_为什么要使用版本控制_哔哩哔哩_bilibili 1.Git必要性 记录代码开发的历史状态 ,允许很多人同时修改文件(分布式)且不会丢失记录 2.版本控制工具应该具备的功能 1)协同修改 多人并行不悖的修改服务器端…...

2309C++均为某个类型
#include <常用> 构 A{空 f(){打印("啊");} }; 元<类 T>构 是点啊:假型{}; 元<>构 是点啊<A>:真型{}; 元<类 T>概念 是呀是点啊<T>::值;元<是呀...T>空 f(T&...t){(t.f(),...); }//均为元<类...T>要求 均为值&l…...

2023年打脸面试官之TCP--瞬间就懂
1.TCP 三次握手之为什么要三次呢?事不过三? 过程如下图: 先来解释下上述的各个标志的含义 序列号seq:占4个字节,用来标记数据段的顺序,TCP把连接中发送的所有数据字节都编上一个序号,第一个字节…...

设计模式-单例模式Singleton
单例模式 单例模式 (Singleton) (重点)1) 为什么要使用单例2) 如何实现一个单例2.a) 饿汉式2.b) 懒汉式2.c) 双重检查锁2.d) 静态内部类2.e) 枚举类2.f) 反射入侵2.g) 序列化与反序列化安全 3) 单例存在的问题3.a) 无法支持面向对象编程 单例模式 (Singleton) (重点) 一个类只…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...

实战设计模式之模板方法模式
概述 模板方法模式定义了一个操作中的算法骨架,并将某些步骤延迟到子类中实现。模板方法使得子类可以在不改变算法结构的前提下,重新定义算法中的某些步骤。简单来说,就是在一个方法中定义了要执行的步骤顺序或算法框架,但允许子类…...
