当前位置： 首页 > news >正文

国产IDE如何获得捐赠和风险投资

news 2026/2/11 6:07:54

有人在开发VB6 脚本工具，有人在开发VB6的插件，把VB6变成VSCODE界面模式，再加上NUGET，NPM等包管理器原理的在线组件、源码下载功能。
还有TWINBASIC几乎80%代替了VB6，radbasic一直封闭，听说也收到了不少众筹的钱。

不知还有谁了解这些内幕？
谁会捐赠美元给IDE开发的个人作者？哪些风投会收购他的公司股份？
如果得不到任何回报，在没钱的情况下，如何坚持2-5年持续开发下去？
目标是什么，动力是什么？

b4a是一个VB语法的安卓APP开发的IDE，以前也要1000美元左右的订阅费用。
B4J是一个vb语法开发IOS APP的IDE。

B4A得到了多少钱的风险投资，有人知道吗？现在他免费给任何人使用了。

We've also secured funds from a US investor who shares my vision of making B4X a popular development tool. These resources will allow us to further expand.

B4A is now free! | Page 8 | B4X Programming Forum
https://www.b4x.com/android/forum/threads/b4a-is-now-free.113678/page-8

It's time to grow 是时候成长了| B4X 编程论坛
https://www.b4x.com/android/forum/threads/its-time-to-grow.113257/

该公司还有开发苹果IOS app的开发工具B4I,开发java的工具b4j
 

相关文章：

国产IDE如何获得捐赠和风险投资

有人在开发VB6 脚本工具，有人在开发VB6的插件，把VB6变成VSCODE界面模式，再加上NUGET，NPM等包管理器原理的在线组件、源码下载功能。 还有TWINBASIC几乎80%代替了VB6，radbasic一直封闭，听说也收到了不少众筹…...

编程日记 2023/9/3 11:30:07

【数学建模】清风数模正课5 相关性分析

相关系数 相关性分析的关键是计算相关系数，在本节课中将会介绍两种常用的相关系数：皮尔逊相关系数（Pearson）和斯皮尔曼相关系数（Spearman）。 它们可以用来衡量两个变量间相关性的大小，对于不同…...

编程日记 2023/9/3 11:29:06

Java设计模式：一、六大设计原则-03：里氏替换原则

文章目录 一、定义：里氏替换原则1.1 里氏替换原则1.2 里氏替换原则的作用 二、模拟场景：里氏替换原则三、违背方案：里氏替换原则3.1 工程结构3.2 储蓄卡和信用卡3.2.1 储蓄卡3.2.2 信用卡 3.3 单元测试3.3.1 储蓄卡测试3.3.2 信用卡测试 四、…...

编程日记 2023/9/3 11:28:05

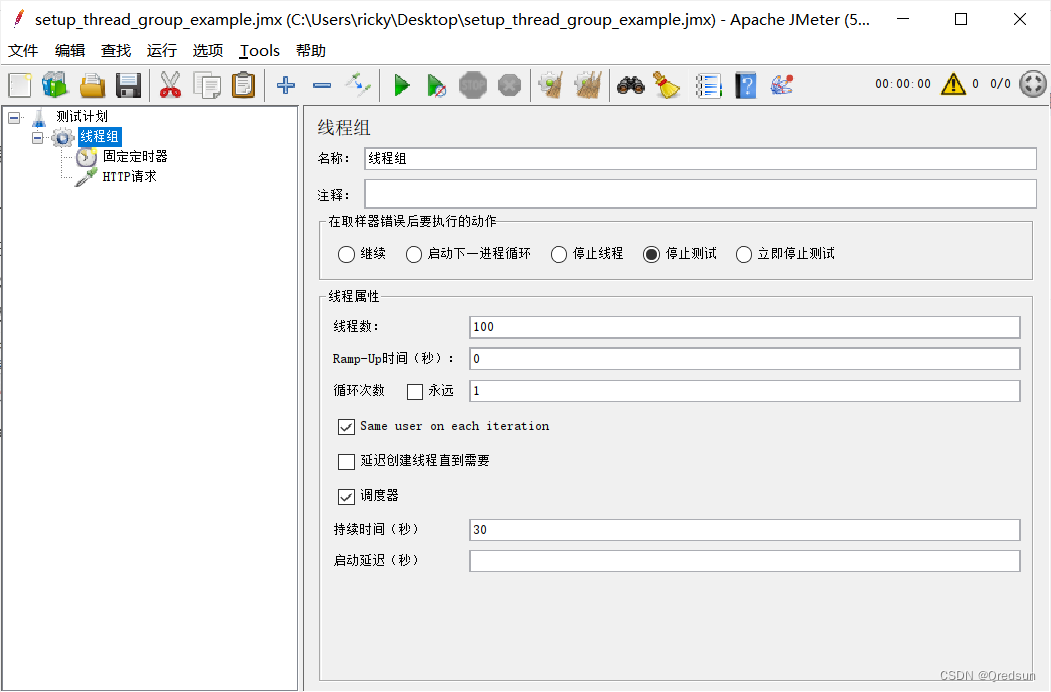
jmeter 固定定时器

固定定时器（Constant Timer）是一个定时器元件，可以在线程组中的每个线程之间添加固定的延迟时间。固定定时器会对每个线程的执行进行一定的暂停。 聊一下和线程组中的调度器对线程组执行时长的影响： 相同： 都会影响线…...

编程日记 2023/9/3 11:27:05

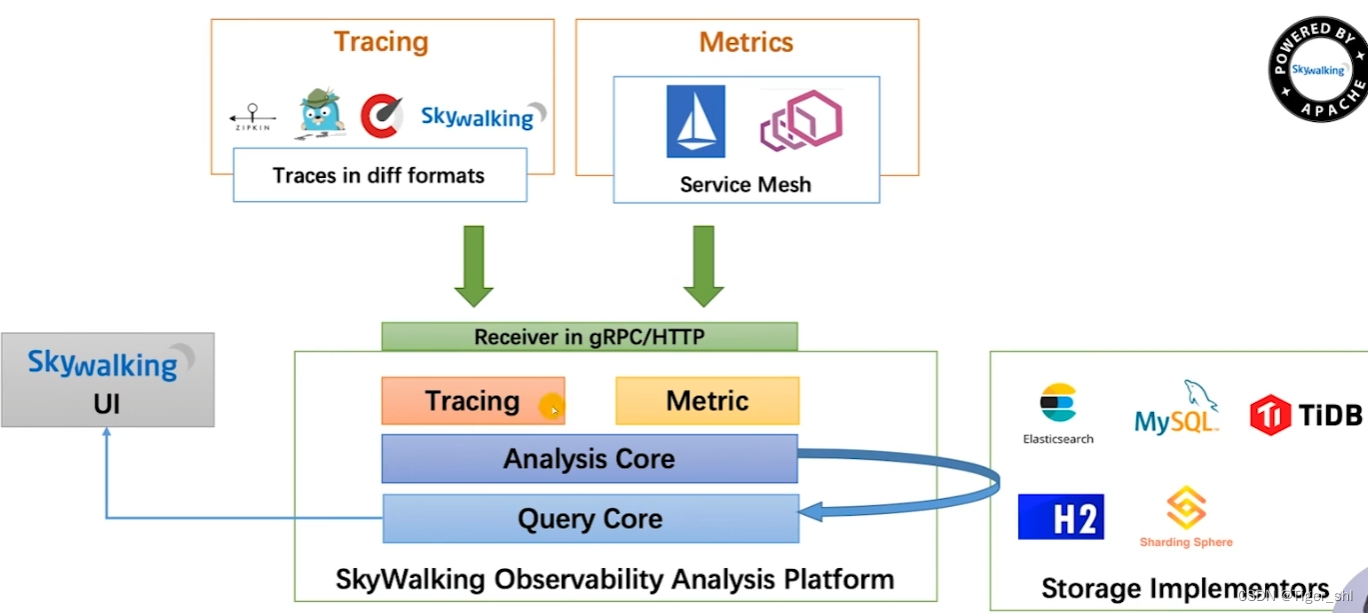
【微服务部署】07-调用链追踪

文章目录 集成SkyWalking实现调用链追踪1. SkyWalking架构图2. 代码集成SkyWalking 集成SkyWalking实现调用链追踪 1. SkyWalking架构图 Receiver是SkyWalking的入口，支持gRPC和HTTP协议。 SkyWalking内部有分析和查询两个部分 存储方面SkyWalking支持Elasticsearc…...

编程日记 2023/9/3 11:26:03

【C++入门】命名空间、缺省参数、函数重载、引用、内联函数

​👻内容专栏： C/C编程 🐨本文概括： C入门学习必备语法 🐼本文作者： 阿四啊 🐸发布时间：2023.9.3 前言 C是在C的基础之上，容纳进去了面向对象编程思想，并增加…...

编程日记 2023/9/3 11:25:02

c++ 学习之 构造函数的使用规则

上规则 // 默认情况下，c 编译器至少给一个类添加三个函数 //1.默认构造函数（无参，函数体为空） //2.默认析构函数 （无参 ，函数体为空） //3.默认拷贝函数，对其属性进行值拷贝 //构…...

编程日记 2023/9/3 11:24:00

C++操作符重载的注意事项

关于C操作符重载&#xff0c;可以用类内的成员运算符重载或友元函数。但是注意两个不能同时出现&#xff0c;不然编译出错。 #include<iostream> using namespace std; class Complex{public:Complex(int r0,int i0){real r;imag i;}//#if 0Complex operator(Complex …...

编程日记 2023/9/3 11:22:59

10 | Spark 查找每个单词的最大行号

假设你有一个包含文本行号和文本内容的RDD，现在你想找出每个单词出现在哪些行，并计算它们出现的最大行号。 需求是从包含文本行号和文本内容的RDD中找出每个单词出现在哪些行，并计算它们出现的最大行号。 具体需求如下： 数据输入： 代码从一个包含文本行号和文本内容的RD…...

编程日记 2023/9/3 11:21:58

CRE66365

CRE66365是一款高度集成的电流模式PWM控制IC&#xff0c;为高性能、低待机功耗和低成本的隔离型反激转换器。在正常负载条件下&#xff0c;AC输入高电压下工作在QR模式。为了最大限度地减少开关损耗&#xff0c;QR 模式下的最大开关频率被内部限制为 77kHz。当负载较低时&#…...

编程日记 2023/9/3 11:20:57

React hook 10种常见 Hook

React Hook是什么&#xff1f; React官网是这么介绍的&#xff1a; Hook 是 React 16.8 的新增特性。它可以让你在不编写 class 的情况下使用 state 以及其他的 React 特性。 完全可选的 你无需重写任何已有代码就可以在一些组件中尝试 Hook。但是如果你不想&#xff0c;你不…...

编程日记 2023/9/3 11:19:56

图文详解PhPStudy安装教程

版权声明 本文原创作者&#xff1a;谷哥的小弟作者博客地址&#xff1a;http://blog.csdn.net/lfdfhl 官方下载 请在PhPStudy官方网站下载安装文件&#xff0c;官方链接如下&#xff1a;https://m.xp.cn/linux.html&#xff1b;图示如下&#xff1a; 请下载PhPStudy安装文件…...

编程日记 2023/9/3 11:18:54

stable diffusion实践操作-hypernetworks

系列文章目录 本文专门开一节写hypernetworks的内容&#xff0c;在看之前&#xff0c;可以同步关注&#xff1a; stable diffusion实践操作 提示&#xff1a;写完文章后&#xff0c;目录可以自动生成&#xff0c;如何生成可参考右边的帮助文档 文章目录 系列文章目录前言一、h…...

编程日记 2023/9/3 11:17:54

Win10搭建VisualSvn Server

Win10搭建VisualSvn Server 目录 Win10搭建VisualSvn Server一、下载VisualSvn Server安装包二、安装VisualSvn Server三、配置和使用VisualSVN Server四、添加用户及权限设定方法五、创建目录及配置权限 1、服务端&#xff1a;有集成了Subversion和Apache、安装使用非常简单且…...

编程日记 2023/9/3 11:16:53

Golang网络编程

Golang网络编程 网络编程简介网络编程协议网络分层模型TCP/IP协议什么是DNS套接字&#xff08;Socket&#xff09;客户端服务器模型TCP/UDP的区别HTTP协议会话sessionCookiehttpsHTTP请求格式HTTP响应格式http头信息http请求头信息http响应头信息HTTP状态码http内容类型和内容…...

编程日记 2023/9/3 11:15:51

详解vue3中ref和reactive用法和区别

vue3中ref和reactive区别 1、前言2、基本用法2.1 ref2.2 reactive 3、ref和reactive定义数组对比3.1 ref定义数组3.1 reactive定义数组 4、ref 和reactive的区别 1、前言 ref和reactive是Vue3中用来实现数据响应式的API&#xff0c;一般情况下&#xff0c;ref定义基本数据类型…...

编程日记 2023/9/3 11:14:50

QML与C++的交互操作

QML旨在通过C 代码轻松扩展。Qt QML模块中的类使QML对象能够从C 加载和操作&#xff0c;QML引擎与Qt元对象系统集成的本质使得C 功能可以直接从QML调用。这允许开发混合应用程序&#xff0c;这些应用程序是通过混合使用QML&#xff0c;JavaScript和C 代码实现的。除了从QML访问…...

编程日记 2023/9/3 11:13:48

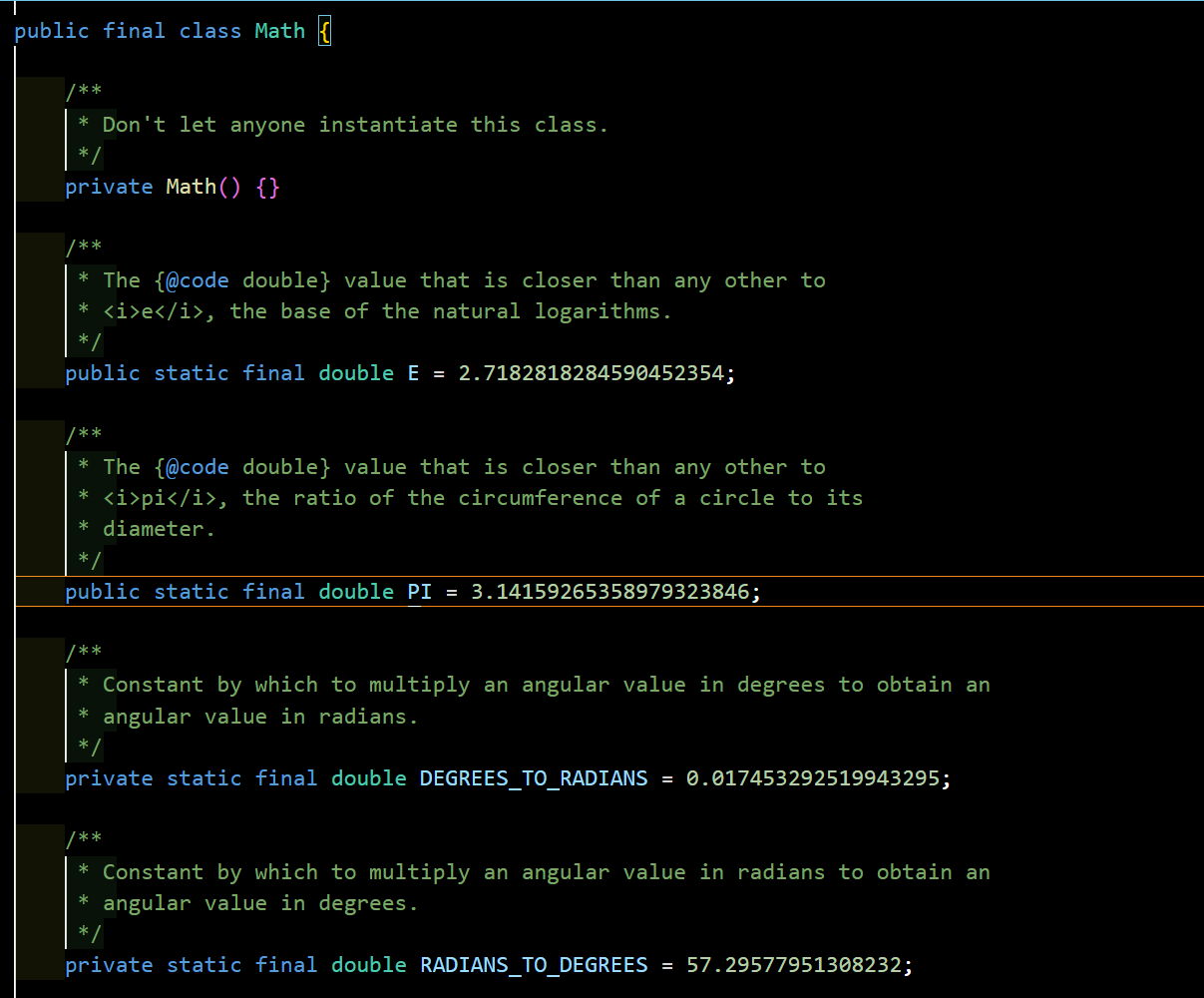
Java_理解方法调用

理解方法调用 首先什么是隐式参数 --->隐式参数是调用该方法的对象本身。 接下来方法的名称和参数列表被称为方法的签名&#xff08;signature&#xff09;。在Java中&#xff0c;方法的签名由方法的名称和参数列表组成&#xff0c;用于唯一标识一个方法。返回类型不是签名的…...

编程日记 2023/9/3 11:12:47

Mysql 性能分析(慢日志、profiling、explain)、读写分离（主从架构）、分库分表（垂直分库、垂直分表、水平分表）

查看系统性能参数 一条sql查询语句在执行前&#xff0c;需要确定查询执行计划&#xff0c;如果存在多种执行计划的话&#xff0c;mysql会计算每个执行计划所需要的成本&#xff0c;从中选择 成本最小的一个作为最终执行的执行计划 想要查看某条sql语句的查询成本&#xff0c;可…...

编程日记 2023/9/3 11:11:46

获取Linux内核源码

在嵌入式平台上做Linux开发的时候&#xff0c;我们用的kernel都是芯片厂家移植到自家平台上的&#xff0c;但是最初的原生Linux内核的源码是从哪里来的呢&#xff1f;下面我们介绍一下怎么获取原生的Linux源码。 从Linux社区获取内核kernel源码 Linux社区的官方网站是 https:…...

编程日记 2023/9/3 11:10:45

（十）学生端搭建

本次旨在将之前的已完成的部分功能进行拼装到学生端&#xff0c;同时完善学生端的构建。本次工作主要包括&#xff1a; 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

编程新知 2026/2/5 4:23:32

相机Camera日志实例分析之二：相机Camx【专业模式开启直方图拍照】单帧流程日志详解

【关注我&#xff0c;后续持续新增专题博文&#xff0c;谢谢&#xff01;&#xff01;&#xff01;】 上一篇我们讲了&#xff1a; 这一篇我们开始讲&#xff1a; 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下&#xff1a; 一、场景操作步骤 操作步…...

编程新知 2026/1/30 10:10:55

23-Oracle 23 ai 区块链表（Blockchain Table）

小伙伴有没有在金融强合规的领域中遇见&#xff0c;必须要保持数据不可变&#xff0c;管理员都无法修改和留痕的要求。比如医疗的电子病历中&#xff0c;影像检查检验结果不可篡改行的&#xff0c;药品追溯过程中数据只可插入无法删除的特性需求&#xff1b;登录日志、修改日志…...

编程新知 2026/2/10 8:01:46

iPhone密码忘记了办？iPhoneUnlocker，iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版​分享

平时用 iPhone 的时候&#xff0c;难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵&#xff0c;或者买了二手 iPhone 却被原来的 iCloud 账号锁住&#xff0c;这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

编程新知 2026/1/29 10:22:28

系统设计 --- MongoDB亿级数据查询优化策略

系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log&#xff0c;共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题&#xff0c;不能使用ELK只能使用…...

编程新知 2026/1/4 3:47:09

将对透视变换后的图像使用Otsu进行阈值化，来分离黑色和白色像素。这句话中的Otsu是什么意思？

Otsu 是一种自动阈值化方法&#xff0c;用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理&#xff0c;能够自动确定一个阈值&#xff0c;将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

编程新知 2026/1/9 19:36:58

Frozen-Flask ：将 Flask 应用“冻结”为静态文件

Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是&#xff1a;将一个 Flask Web 应用生成成纯静态 HTML 文件&#xff0c;从而可以部署到静态网站托管服务上&#xff0c;如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

编程新知 2025/12/5 20:57:13

算法：模拟

1.替换所有的问号 1576. 替换所有的问号 - 力扣&#xff08;LeetCode&#xff09; ​遍历字符串​&#xff1a;通过外层循环逐一检查每个字符。​遇到 ? 时处理​&#xff1a; 内层循环遍历小写字母&#xff08;a 到 z&#xff09;。对每个字母检查是否满足&#xff1a; ​与…...

编程新知 2026/2/10 11:15:52

push [特殊字符] present

push &#x1f19a; present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中&#xff0c;push 和 present 是两种不同的视图控制器切换方式&#xff0c;它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

编程新知 2026/1/31 4:26:17

LLMs 系列实操科普（1）

写在前面&#xff1a; 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容&#xff0c;原视频时长 ~130 分钟&#xff0c;以实操演示主流的一些 LLMs 的使用&#xff0c;由于涉及到实操&#xff0c;实际上并不适合以文字整理&#xff0c;但还是决定尽量整理一份笔…...

编程新知 2026/1/31 11:35:24