代码随想录 - Day31 - 回溯:组合问题
代码随想录 - Day31 - 回溯:组合问题
77. 组合
最容易想到的:k层for循环。
显然不能写那么多层for循环,所以该方法pass
使用回溯法:
用递归解决嵌套层数的问题
n相当于树的宽度,k相当于树的深度。
找到最深处的叶子节点即为找到一个结果,把结果收集起来就是最终答案。
class Solution:def combine(self, n: int, k: int) -> List[List[int]]:result = [] # 存放结果集self.backtracking(n, k, 1, [], result)return resultdef backtracking(self, n, k, startIndex, path, result):if len(path) == k:result.append(path[:])returnfor i in range(startIndex, n + 1): # 需要优化的地方path.append(i) # 处理节点self.backtracking(n, k, i + 1, path, result)path.pop() # 回溯,撤销处理的节点
剪枝优化:
可以剪枝的地方就在递归中每一层的for循环所选择的起始位置。
如果for循环选择的起始位置之后的元素个数已经不足需要的元素个数了,那就没必要搜索了。
优化过程:
- 已经选择的元素个数:path.size();
- 还需要的元素个数为: k - path.size();
- 在集合n中至多要从该起始位置 : n - (k - path.size()) + 1,开始遍历
为什么有个+1呢,因为包括起始位置,我们要是一个左闭的集合。
class Solution:def combine(self, n: int, k: int) -> List[List[int]]:result = [] # 存放结果集self.backtracking(n, k, 1, [], result)return resultdef backtracking(self, n, k, startIndex, path, result):if len(path) == k:result.append(path[:])returnfor i in range(startIndex, n - (k - len(path)) + 2): # 剪枝优化path.append(i) # 处理节点self.backtracking(n, k, i + 1, path, result)path.pop() # 回溯,撤销处理的节点
216. 组合总和 III
找到和为n的k个数的组合,且k在1~9之间
class Solution:def combinationSum3(self, k: int, n: int) -> List[List[int]]:result = [] # 存放结果集self.backtracking(n, k, 0, 1, [], result)return resultdef backtracking(self, targetSum, k, currentSum, startIndex, path, result):if currentSum > targetSum: # 剪枝操作return # 如果path的长度等于k但currentSum不等于targetSum,则直接返回if len(path) == k and currentSum == targetSum:result.append(path[:])returnfor i in range(startIndex, 10): # 剪枝优化currentSum += ipath.append(i) # 处理节点self.backtracking(targetSum, k, currentSum, i + 1, path, result)currentSum -= ipath.pop() # 回溯,撤销处理的节点
剪枝优化:
已选元素总和如果已经大于n了,那么往后遍历就没有意义了,直接剪掉。
class Solution:def combinationSum3(self, k: int, n: int) -> List[List[int]]:result = [] # 存放结果集self.backtracking(n, k, 0, 1, [], result)return resultdef backtracking(self, targetSum, k, currentSum, startIndex, path, result):if currentSum > targetSum: # 剪枝操作return # 如果path的长度等于k但currentSum不等于targetSum,则直接返回if len(path) == k and currentSum == targetSum:result.append(path[:])returnfor i in range(startIndex, 9 - (k - len(path)) + 2): # 剪枝优化currentSum += ipath.append(i) # 处理节点self.backtracking(targetSum, k, currentSum, i + 1, path, result)currentSum -= ipath.pop() # 回溯,撤销处理的节点
在一开始判断的时候不能把if currentSum > targetSum写在if len(path) == k里面。如果写在里面,就忽略掉了currentSum > targetSum && len(path) != k的情况。
17. 电话号码的字母组合
使用map或定义一个二维数组,实现数字和字母的映射
def __init__(self):self.letterMap = ["", # 0"", # 1"abc", # 2"def", # 3"ghi", # 4"jkl", # 5"mno", # 6"pqrs", # 7"tuv", # 8"wxyz" # 9]self.result = [] # 记录结果self.s = "" # 字符串s来收集叶子节点的结果
完整代码:
class Solution:def __init__(self):self.letterMap = ["", # 0"", # 1"abc", # 2"def", # 3"ghi", # 4"jkl", # 5"mno", # 6"pqrs", # 7"tuv", # 8"wxyz" # 9]self.result = []self.s = []def backtracking(self, digits, index):if index == len(digits):self.result.append("".join(self.s))returndigit = int(digits[index])letters = self.letterMap[digit]for i in range(len(letters)):self.s.append(letters[i])self.backtracking(digits, index + 1)self.s.pop()def letterCombinations(self, digits: str) -> List[str]:if len(digits) == 0:return self.resultself.backtracking(digits, 0)return self.result
由于题目中限定了2~9,所以并未考虑0和1没有对应字母的情况。在实际问题中应当考虑到。
小总结
做了这几道题后,发现它们的解题代码都有共通之处,于是自己总结了一下。
def __init__(): # 需要的时候才写# 定义全局变量def backtracking(self, 参数1, 参数2, ...):# 回溯算法if 相等:result.append()returnfor ...:# 回溯代码self.backtracking() # 递归# 回溯代码def function():# 排除某些情况self.backtracking() # 递归return result
相关文章:

代码随想录 - Day31 - 回溯:组合问题
代码随想录 - Day31 - 回溯:组合问题 77. 组合 最容易想到的:k层for循环。 显然不能写那么多层for循环,所以该方法pass 使用回溯法: 用递归解决嵌套层数的问题 n相当于树的宽度,k相当于树的深度。 找到最深处的叶子节…...
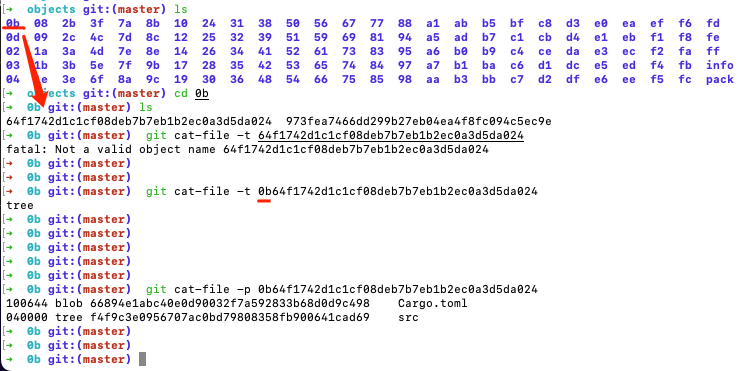
git文件夹内容详解
.git文件夹是Git版本控制系统在项目根目录下创建的隐藏文件夹,包含了Git仓库的所有相关信息。如下是.git文件夹中常见的一些内容及其作用: HEAD:指向当前所在的分支(或者是一个特定的提交)。 branches:存储…...
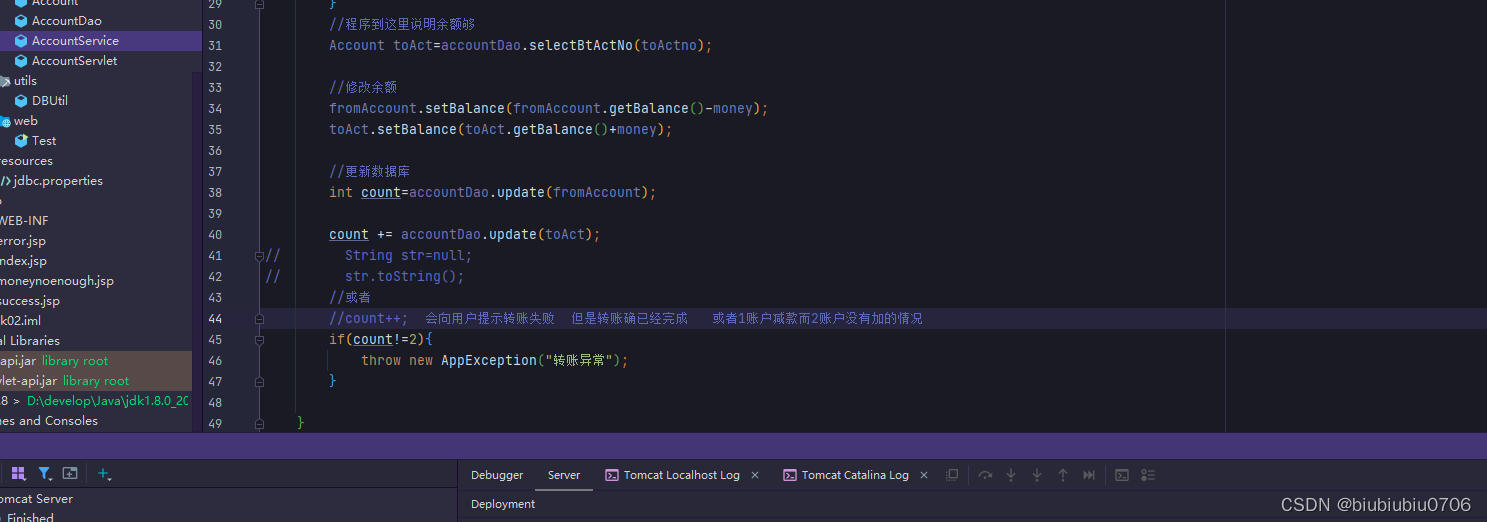
MVC模式分层练习
新建库 新建表 插入点数据 先不用MVC模式写功能,来看下缺点是什么 新建一个空项目 选项项目使用的JDK 自己的IDEA总是要重启下 新建模块 因maven还没教 添加框架支持 添加后项目多了这些 添加些必要依赖 这里注意下,如果导入jar包不对可以重新导入下或者是jar包本身出了问…...

ORB-SLAM2算法12之单目初始化Initializer
文章目录 0 引言1 单目初始化Initializer1.1 构造函数1.2 成员函数1.2.1 Initialize1.2.2 FindHomography1.2.3 FindFundamental1.2.4 ReconstructH1.2.5 ReconstructF 2 总结 0 引言 ORB-SLAM2算法7详细了解了System主类和多线程、ORB-SLAM2学习笔记8详细了解了图像特征点提取…...

固定参数-以京东sign逆向为例
前言 在逆向过程中,需要结合frida或unidbg,对整个算法进行一步步的分析,有时候我们分析完某一部分,想要继续往下分析时,需要重新发起请求,这时候的参数往往都已经改变了,这样会打断我们的节奏&a…...

在macOS 上执行sed命令报错问题
错误描述 在macOS 上执行sed命令,报错 sed -i s/book/books/g demo.txt sed: 1: extra characters at the end of d command解决方法 原因是mac的和linux写法不一样 linux sed -i s/book/books/g demo.txtmac sed -i s/book/books/g demo.txt...

ARP欺骗
ARP协议: 地址解析协议,将IP地址转换为对应的mac地址,属链路层协议 ip地址: ip地址本义是为互联网上的每一个网络和每一台主机配置一个唯一的逻辑地址,它的格式表示为:(A.B.C.D)。其…...
)
pip切换下载源(多种国内源)
pip切换下载源 一、pip二、使用步骤1.查看源2.切换源 一、pip pip 是一个现代的,通用的 Python 包管理工具 二、使用步骤 1.查看源 使用以下命令查看当前pip的下载源 pip config list2.切换源 在国内使用官方下载依赖往往速度慢,易出错,…...

ARM Cortex-M 的 SP
文章目录 1、栈2、栈操作3、Cortex-M中的栈4、MDK中的SP操作流程5、Micro-Lib的SP差别1. 使用 Micro-Lib2. 未使用 Micro-Lib 在嵌入式开发中,堆栈是一个很基础,同时也是非常重要的名词,堆栈可分为堆 (Heap) 和栈 (Stack) 。 栈(Stack): 一种…...
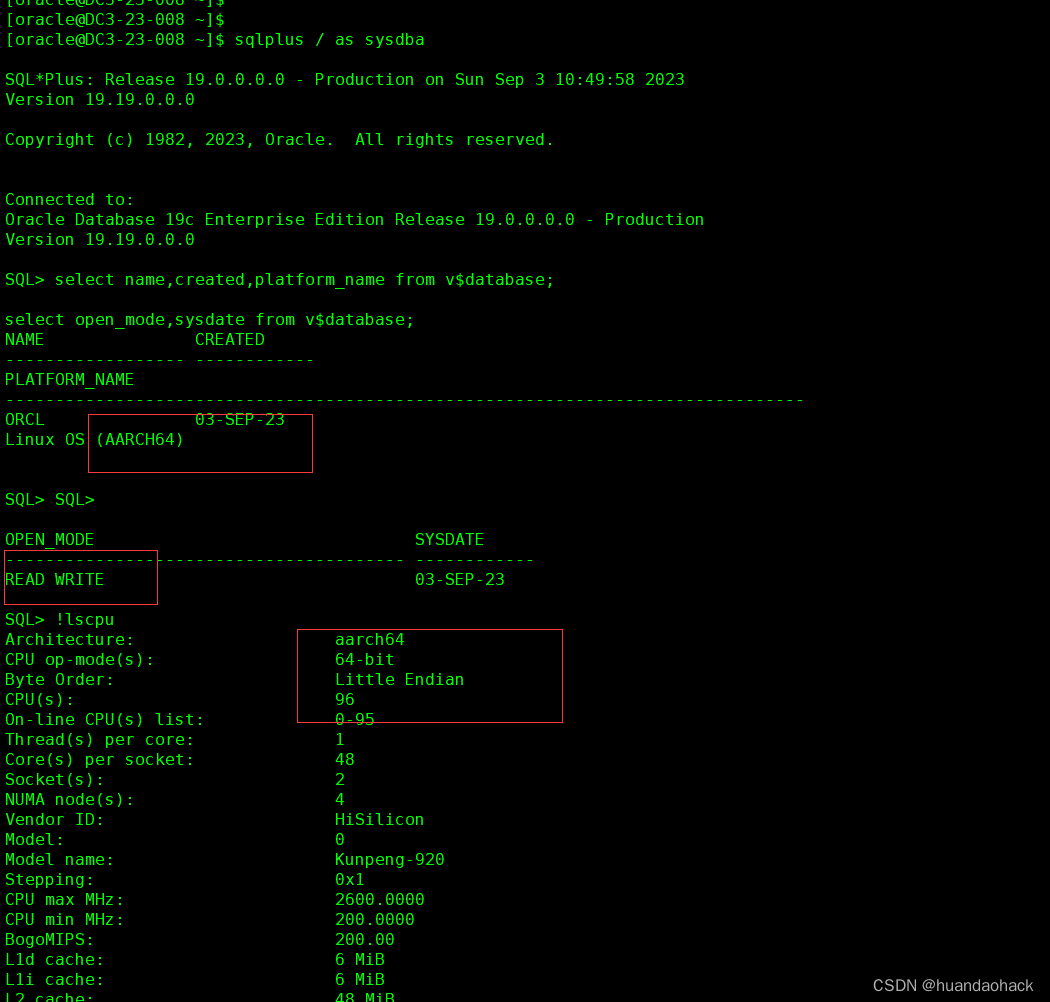
【原创】鲲鹏ARM构架openEuler操作系统安装Oracle 19c
作者:einyboy 【原创】鲲鹏ARM构架openEuler操作系统安装Oracle 19c | 云非云计算机科学、自然科学技术科谱http://www.nclound.com/index.php/2023/09/03/%E3%80%90%E5%8E%9F%E5%88%9B%E3%80%91%E9%B2%B2%E9%B9%8Farm%E6%9E%84%E6%9E%B6openeuler%E6%93%8D%E4%BD%9C%E7%B3%BB%…...

k8s之存储篇---数据卷-挂载
挂载是指将定义在 Pod 中的数据卷关联到容器,同一个 Pod 中的同一个数据卷可以被挂载到该 Pod 中的多个容器上。 数据卷内子路径 有时候我们需要在同一个 Pod 的不同容器间共享数据卷。使用 volumeMounts.subPath 属性,可以使容器在挂载数据卷时指向数…...

无涯教程-JavaScript - TDIST函数
The TDIST function replaces the T.DIST.2T & T.DIST.RT functions in Excel 2010. 描述 该函数返回学生t分布的百分点(概率),其中数值(x)是t的计算值,将为其计算百分点。 t分布用于小样本数据集的假设检验。使用此函数代替t分布的临界值表。 语法 TDIST(x,deg_fr…...
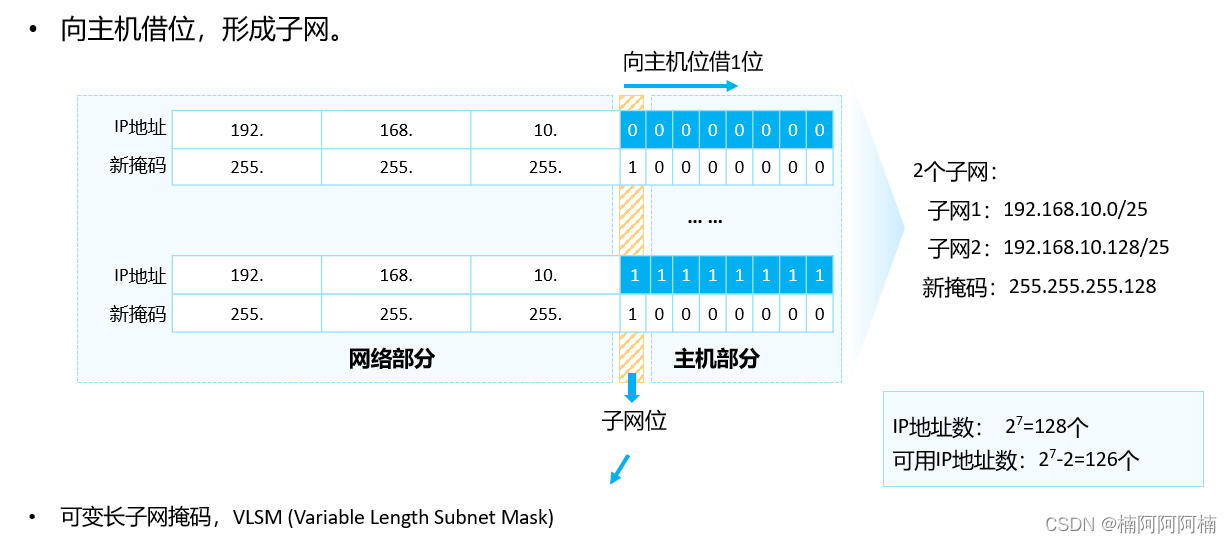
IP子网的划分
文章目录 一、子网掩码1. 产生背景2. 定义3. 分类 二、VLSM算法1. 得出下列参数2. 计算划分结果3. 举例子计算 三、常见子网划分对应关系四、练习IP编址题目需求解题1. 192.168.1.100/282. 172.16.0.58/263. 25.83.149.222/254. 100.100.243.18/205. 10.100.100.100/10 首先可以…...
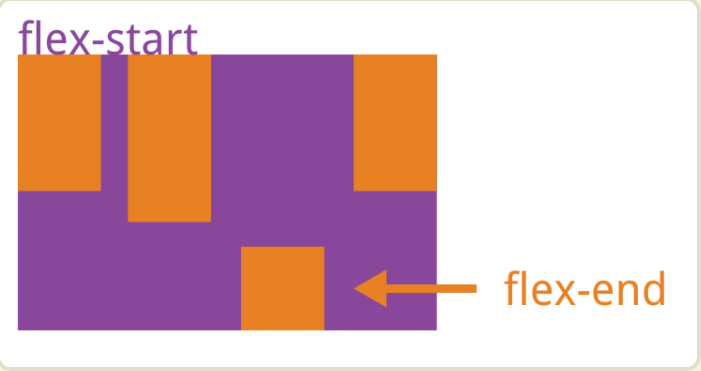
弹性盒子的使用
一、定义 弹性盒子是一种用于按照布局元素的一维布局方法,它可以简便、完整、响应式地实现各种页面布局。 容器中存在两条轴,主轴和交叉轴(相当于我们坐标轴的x轴和y轴)。我们可以通过flex-direction来决定主轴的方向。 主轴(main axis&am…...

软件测试/测试开发丨Selenium 网页frame与多窗口处理
点此获取更多相关资料 本文为霍格沃兹测试开发学社学员学习笔记分享 原文链接:https://ceshiren.com/t/topic/27048 一、多窗口处理. 1.1、多窗口简介 点击某些链接,会重新打开⼀个窗⼜,对于这种情况,想在新页⾯上操作࿰…...
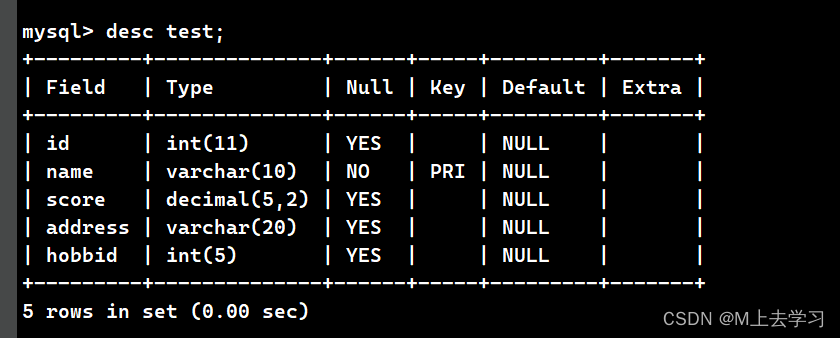
MySQL高阶语句(三)
一、NULL值 在 SQL 语句使用过程中,经常会碰到 NULL 这几个字符。通常使用 NULL 来表示缺失 的值,也就是在表中该字段是没有值的。如果在创建表时,限制某些字段不为空,则可以使用 NOT NULL 关键字,不使用则默认可以为空…...
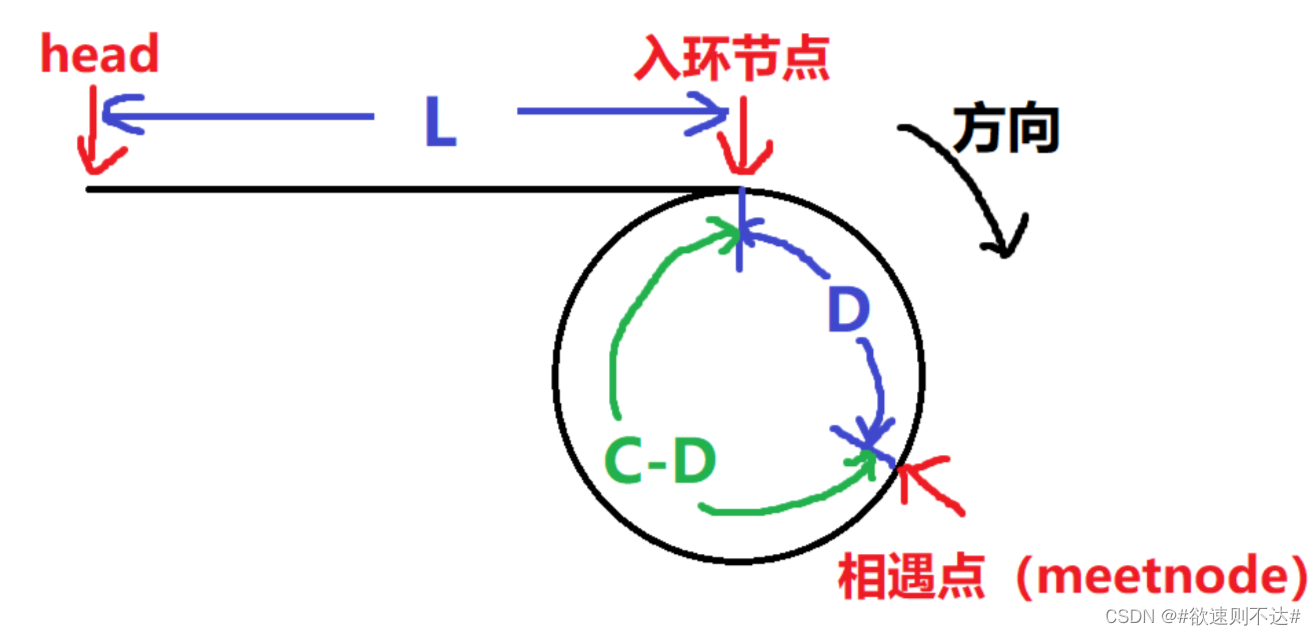
链表OJ练习(2)
一、分割链表 题目介绍: 思路:创建两个链表,ghead尾插大于x的节点,lhead尾插小于x的节点。先遍历链表。最后将ghead尾插到lhead后面,将大小链表链接。 我们需要在创建两个链表指针,指向两个链表的头节点&…...

ssh常用操作
ssh常用操作 SSH是一种安全协议,ssh是该协议的客户端程序,openssh-server则是该协议的服务端程序 常用系统都自带了ssh客户端程序,服务端程序则可能要安装 密码远程登陆 前提:服务器安装了openssh-server,未安装时…...

从AD迁移至AAD,看体外诊断领军企业如何用网络准入方案提升内网安全基线
摘要: 某医用电子跨国集团中国分支机构在由AD向AzureAD Global迁移时,创新使用宁盾网络准入,串联起上海、北京、无锡等国内多个职场与海外总部,实现平滑、稳定、全程无感知的无密码认证入网体验,并通过合规基线检查,确…...

Flutter系列文章-Flutter在实际业务中的应用
不同场景下的解决方案 1. 跨平台开发: 在移动应用开发中,面对不同的平台(iOS和Android),我们通常需要编写两套不同的代码。而Flutter通过一套代码可以构建适用于多个平台的应用,大大提高了开发效率&#x…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

使用ch340继电器完成随机断电测试
前言 如图所示是市面上常见的OTA压测继电器,通过ch340串口模块完成对继电器的分路控制,这里我编写了一个脚本方便对4路继电器的控制,可以设置开启时间,关闭时间,复位等功能 软件界面 在设备管理器查看串口号后&…...

VSCode 没有添加Windows右键菜单
关键字:VSCode;Windows右键菜单;注册表。 文章目录 前言一、工程环境二、配置流程1.右键文件打开2.右键文件夹打开3.右键空白处打开文件夹 三、测试总结 前言 安装 VSCode 时没有注意,实际使用的时候发现 VSCode 在 Windows 菜单栏…...

Shell 解释器 bash 和 dash 区别
bash 和 dash 都是 Unix/Linux 系统中的 Shell 解释器,但它们在功能、语法和性能上有显著区别。以下是它们的详细对比: 1. 基本区别 特性bash (Bourne-Again SHell)dash (Debian Almquist SHell)来源G…...

使用VMware克隆功能快速搭建集群
自己搭建的虚拟机,后续不管是学习java还是大数据,都需要集群,java需要分布式的微服务,大数据Hadoop的计算集群,如果从头开始搭建虚拟机会比较费时费力,这里分享一下如何使用克隆功能快速搭建一个集群 先把…...
