归并排序的详解!
本文旨在讲解归并排序的实现(递归及非递归)搬好小板凳,干货来了!
前序:
在介绍归并排序之前,需要给大家介绍的是什么是归并,归并操作,也叫归并算法,指的是将两个顺序序列合并成一个顺序序列的方法,相信不少小伙伴之前都做过合并两个有序链表或者两个有序数组的例题,归并就是将两个数组或链表合并成一个链表或数组,还得保证与其原来的顺序相同!那么归并排序就是用到了归并这个思想,将一组元素完成排序的算法!
归并排序的介绍
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
归并排序的时间复杂度和空间复杂度
时间复杂度:O(N*logN),因为其是一种二叉树结构,其高度为logN,每层需要排序的个数都是N个,所以其时间复杂度为O(N*logN)。
空间复杂度:因为创建了一个新的数组,所以其空间复杂度为O(N);
归并排序的思想与思路
归并排序就是本质上是分治的方法来实现的,是将一组数据分割成若干组有序数组,然后对这若干个有序数组两两进行归并即可得到我们想要的排序!
归并排序的思路图
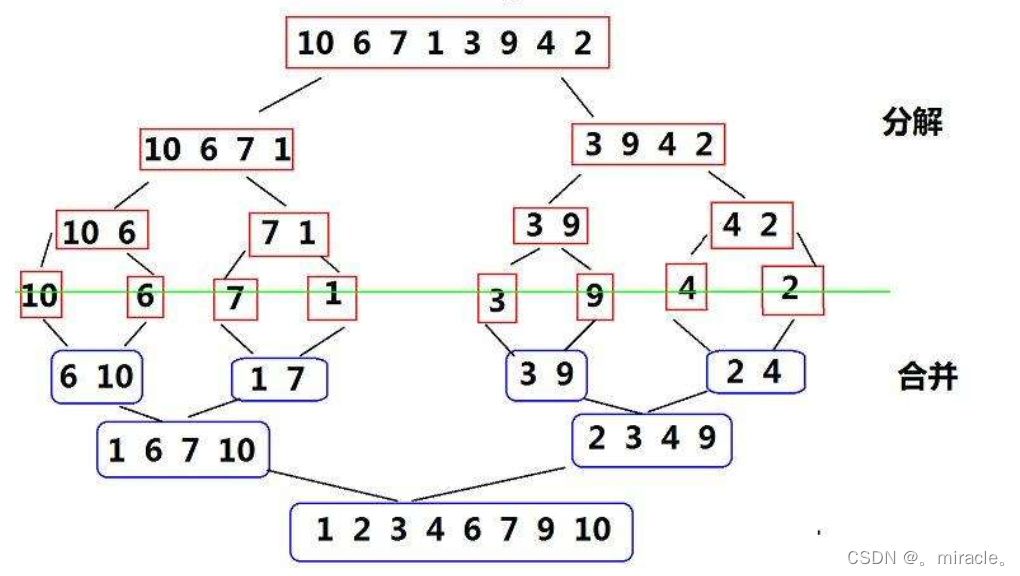
归并排序的动态图展示

归并排序的大致实现思路
归并排序其实现的思路其实很简单,就是将一组数据分割,分割到若干组有序数组,然后两两进行归并,那么如何保证分割的数组为有序数组呢,这其实很简单,当分割到数组中只有一个元素的时候,那么该数组就是有序的数组了!然后进行归并拷贝到原数组上即可!
归并排序的代码实现
(C版本递归)
void _MergeSort(int* a, int left, int right, int* tem)
{//当再次需要调用的区间不存在时,返回即可!if (left == right) //很显然,left不会大于right,保险起见,加上大于条件没有影响!{return;}//每次取出中间坐标,用于下次的左半边的递归,右半边递归同理!int mid = (left + right) / 2;_MergeSort(a, left, mid, tem);_MergeSort(a, mid + 1, right, tem);//到此,分割区间已经结束,每组区间都能保证时有序的了!下一步就开始进行归并!int begin1 = left, end1 = mid;int begin2 = mid + 1, end2 = right;int i = left; //i用于对tem数组的下标进行表示!//下面开始归并两个有序数组,当两个有序数组其中一个遍历完成就退出循环!while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tem[i++] = a[begin1++];}else{tem[i++] = a[begin2++];}}while (begin1 <= end1){tem[i++] = a[begin1++];}while (begin2 <= end2){tem[i++] = a[begin2++];}//归并结束后,将tem数组中的数据,拷贝到元素组中相应的位置即可!memcpy(a + left, tem + left, sizeof(int)*(right - left + 1));//个数为右边界减去左边加1,因为为闭区间!//至此,归并结束,拷贝结束!
}
void MergeSort(int* a, int n)
{//在堆上申请开辟一个tem数组,用来最后拷贝到原数组中!int* tem = (int *)malloc(sizeof(int) * n);//因为存在递归的调用,所以再创建一个函数,若仍在此函数上重复调用时,则会重复开辟新的空间,可能导致空间不足!_MergeSort(a, 0, n - 1, tem);//用完之后释放到tem数组!free(tem);
}需要注意的是:当进行递归归并排序的时候,需要注意返回的条件,当区间不存在或者区间内部只有一个元素的时候就可以返回了!还需要注意的是,因为要进行拷贝,不能在原数组上直接拷贝,所以需要创建一个新的数组用来存储归并后的元素的位置,最后归并结束重新拷贝到原数组中即可!
(C版本非递归)
分段拷贝
// 归并排序非递归实现//思路如下:要想实现归并排序的非递归,那么需要注意分组,从每组一个元素开始,因为当只有一个元素的时候,默认是有序的,然后
//进行归并拷贝即可,每组一个元素遍历结束之后,进行每组两个,依次进行每组2倍个元素进行归并!,当每组的元素为所有元素的一半或大于一半,
//即可完成排序,需要特别注意的是,进行非递归归并排序的时候,需要注意区间的取值,在此有两个拷贝方式,一种是整体拷贝,一组是归并一段拷贝一段!//进行非递归实现归并的时候也需要创建一个新的数组,不能在原数组上进行对数据的改变,因为可能会造成数据的覆盖,导致数据不能完成排序!
//创建一个新数组,然后让每组元素为一个依次递增二倍,进行归并拷贝,直至每组的元素个数大于数组个数结束归并即可完成排序!//下面先来进行分段拷贝!
//void MergeSortNonR(int* a,int n)
//{
// //注意:gap代表的是每组归并时的元素的个数!
// int gap = 1;
// int* tem = (int*)malloc(sizeof(int) * n);
// while (gap < n) //当gap大于n时结束循环即可完成!
// {
// int j = 0;
// //每组为一个的进行遍历!
// for (int i = 0; i <n ; i+=2*gap)
// {
//
// //每组个数为1的进行归并排序!
// //区间范围如下!
// int begin1 = i, end1 = i + gap - 1;
// int begin2 = i + gap, end2 = i + 2 * gap - 1;
//
// //当end1>n,begin2>n时,不需要进行归并!
// if (end1 >= n||begin2>=n)
// {
// break;
// }
//
// //对end2边界进行修改!
// if (end2 >= n)
// {
// end2 = n-1;
// }
//
// //开始进行归并拷贝!
// while (begin1 <= end1 && begin2 <= end2)
// {
// if (a[begin1] < a[begin2])
// {
// tem[j++] = a[begin1++];
// }
// else
// {
// tem[j++] = a[begin2++];
// }
// }
// while (begin1 <= end1)
// {
// tem[j++] = a[begin1++];
// }
// while (begin2 <= end2)
// {
// tem[j++] = a[begin2++];
// }
//
// //注意:需要注意的是:当求元素的个数时,应该用end2-i,不能减去begin1,因为begin1每次都会改变,记录的不再是数组开始拷贝的地方!
// memcpy(a + i, tem + i, sizeof(int) * (end2 - i + 1));
// }
// gap *= 2;
// }
// free(tem);
//}整体拷贝
//整段拷贝!
void MergeSortNonR(int* a, int n)
{//注意:gap代表的是每组归并时的元素的个数!int gap = 1;int* tem = (int*)malloc(sizeof(int) * n);while (gap < n) //当gap大于n时结束循环即可完成!{//j的声明必须写在for循环的外面,因为若写到for循环内部时,在每组循环都会将原来归并好的数据放到前面的那些位置//导致以及归并好的又被覆盖,导致排序失败!(每组的归并都放在前两组内部,导致不能将全部归并结束,!)int j = 0;//每组为一个的进行遍历!for (int i = 0; i < n; i += 2 * gap){//每组个数为1的进行归并排序!//区间范围如下!int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;//当end1>n,begin2>n时,不需要进行归并!if (end1 >= n){end1 = n - 1;//将第二块区间设置为不存在的区间!如果设置为n-1那么会造成对最后一个数据的重复使用,拷贝,导致排序错误!begin2 = n;end2 = n - 1;}else if (begin2 >= n){begin2 = n;end2 = n - 1;}else if(end2>=n){end2 = n - 1;}//开始进行归并拷贝!while (begin1 <= end1 && begin2 <= end2){if (a[begin1] <= a[begin2]){tem[j++] = a[begin1++];}else{tem[j++] = a[begin2++];}}while (begin1 <= end1){tem[j++] = a[begin1++];}while (begin2 <= end2){tem[j++] = a[begin2++];}//注意:需要注意的是:进行整段拷贝的时候,不需要再从a+begin1的位置开始拷贝啦,直接将所有tem中的元素拷贝到原数组即可!}memcpy(a, tem, sizeof(int) * n);gap *= 2;}free(tem);
}需要注意的是:非递归的归并排序,整体拷贝和分段拷贝大致思路是一样的,只是最后进行memcpy的起始位置和个数有所不同!相关细节与思路都在源代码上加有注释标明,需要注意的是:当进行整体拷贝的时候,用于标记tem数组的j的坐标的定义一定要在for循环外部定义赋值,若在内部赋值定义,则每进行一次都会覆盖原来已经归并好的数据上面,导致归并排序不能正确进行!
今日的归并排序分享到此结束,欢迎大家积极评论支持。若有不足及补充,及时提出,必将改正!

相关文章:

归并排序的详解!
本文旨在讲解归并排序的实现(递归及非递归)搬好小板凳,干货来了! 前序: 在介绍归并排序之前,需要给大家介绍的是什么是归并,归并操作,也叫归并算法,指的是将两个顺序序列…...

排盘程序算法探寻举例(陆先生八字)
算法实现: 1.庚生未月,燥土不能生金,日支申金为日主墙根,月干辛金比劫透出傍身,月干强。年干甲木自做寅木强根,又得月支乙木中气,甲木强旺有力,时干丙火七杀得未土余气,…...

考研408 | 【操作系统】终章
I/O设备的基本概念和分类 I/O设备: I/O设备的分类 1.按使用特性: 2.按传输速率分类: 3.按信息交换的单位分类: 总结: I/O控制器 I/O设备的机械部件: I/O设备的电子部件(I/O控制器&#…...
亚马逊云科技生成式AI技术辅助教学领域,近实时智能应答2D数字人搭建
早在大语言模型如GPT-3.5等的兴起和被日渐广泛的采用之前,教育行业已经在AI辅助教学领域有过各种各样的尝试。在教育行业,人工智能技术的采用帮助教育行业更好地实现教学目标,提高教学质量、学习效率、学习体验、学习成果。例如,人…...

Programming abstractions in C阅读笔记:p139-p143
《Programming Abstractions In C》学习第55天,p139-p140,总结如下: 一、技术总结 1.文件I/O操作 文件I/O操作可以分为一下这些步骤: (1)声明文件指针对象。 File *infile;(2)打开文件 fopen()。打开文件的模式有“r”, “w…...
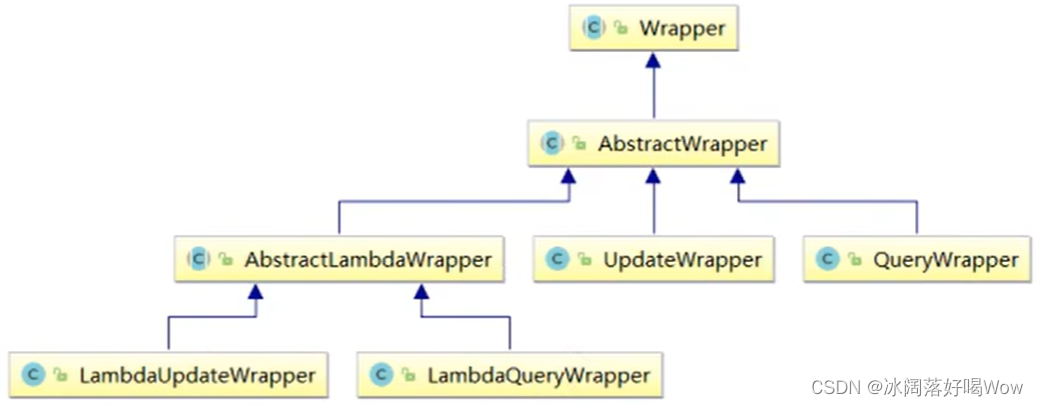
MyBatis-Plus学习笔记
1.MyBatis-Plus简介: MyBatis-Plus是一个MyBatis的增强工具,在MyBatis的基础上只做增强不做改变,为简化开发、提高效率而生。MyBatis-Plus提供了通用的mapper和service,可以在不编写任何SQL语句的情况下,快速的实现对单…...
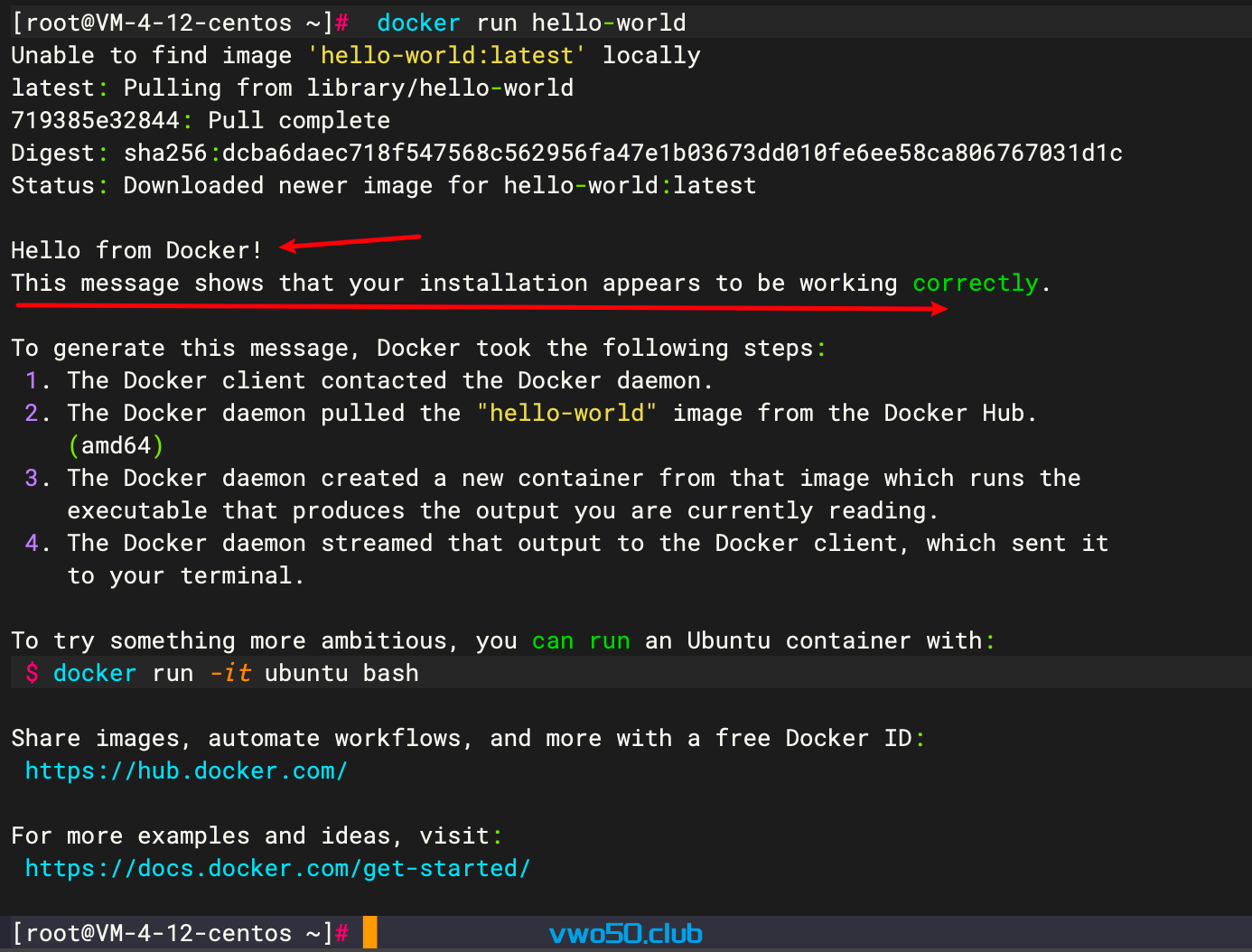
linux安装docker全过程
3. 第二步:设置docker的存储库。就两条命令,我们直接执行就好。 sudo yum install -y yum-utils sudo yum-config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo 4. 安装docker engine和docker-compose。 执行命…...

Spring 中存取 Bean 的相关注解
目录 一、五大类注解 1、五大类注解存储Bean对象 1.1Controller(控制器储存) 1.2Service(服务存储) 1.3Repository(仓库存储) 1.4Component(组件存储) 1.5Configuration(配置存储) 2、五大类注解小结 2.1为什么要这么多类注解 2.2 五大类注解之间的关系 二、方法注解 1.方法注…...

Camunda 7.x 系列【38】表单服务 FormService
有道无术,术尚可求,有术无道,止于术。 本系列Spring Boot 版本 2.7.9 本系列Camunda 版本 7.19.0 源码地址:https://gitee.com/pearl-organization/camunda-study-demo 文章目录 1. 概述2. 演示2.1 获取流程开始表单2.2 启动流程2.3 查询任务表单2.4 完成任务3. 实际开发…...
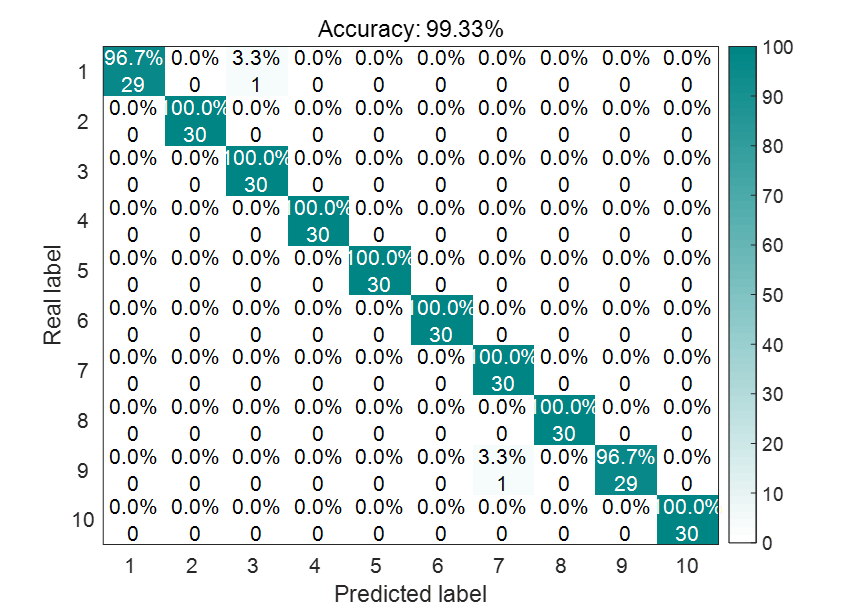
保姆级教程之SABO-VMD-SVM的西储大学轴承诊断
之前写过一篇优化核极限学习机的轴承诊断,今天再出一期基于SVM的轴承诊断。 依旧是包含了从数据处理,到减法优化器SABO算法优化VMD参数,再到支持向量机的故障诊断,实现故障诊断的全流程,其他类型的故障诊断均可参考此流…...
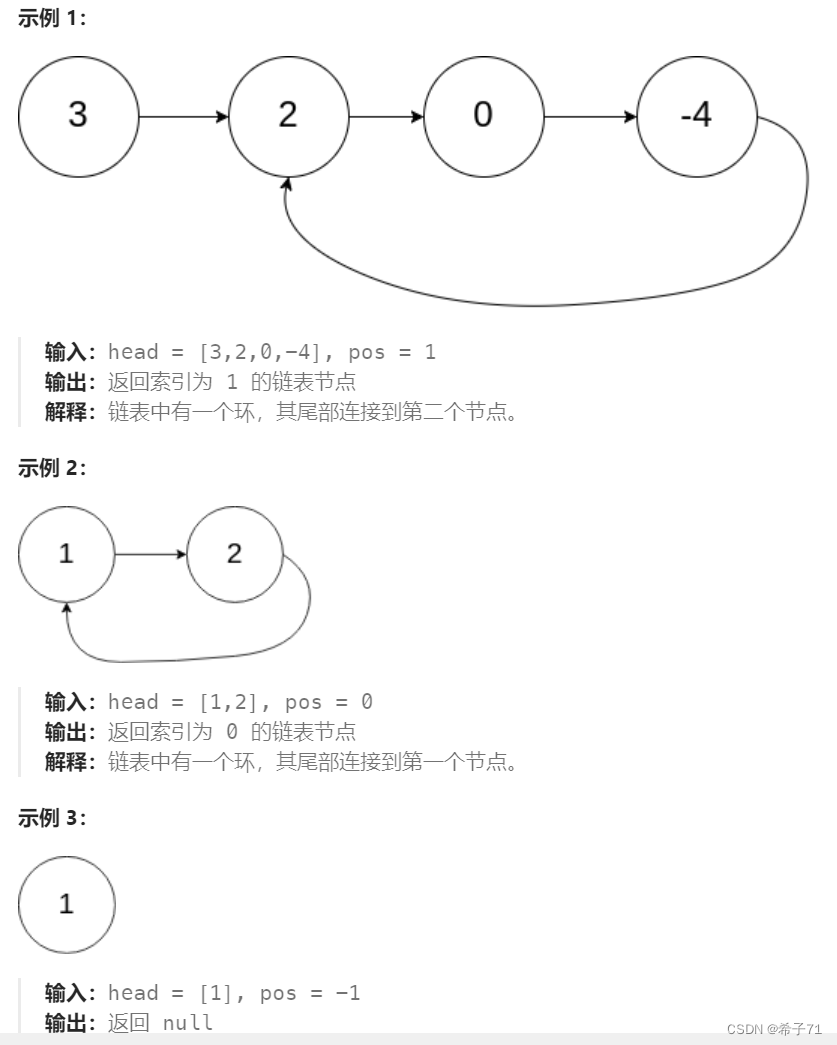
指向任意节点的带环链表
🌈图示指向任意节点的带环链表 如图: 🌈快慢指针法判断链表是否带环 🌟思路:快指针fast一次走2步,慢指针slow一次走1步,fast先进环在换中运动,随后slow进入环。两指针每同时移动…...
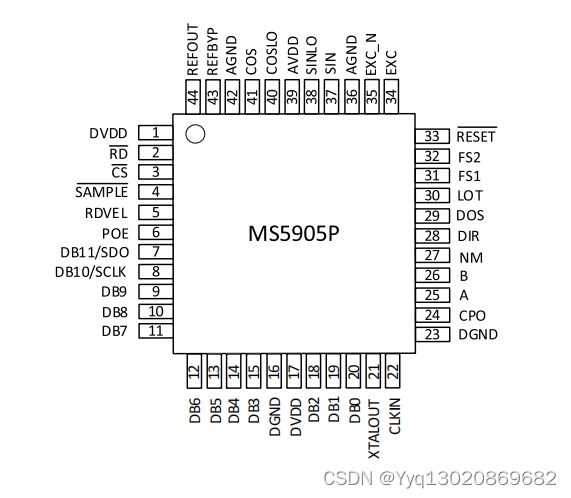
应用于伺服电机控制、 编码器仿真、 电动助力转向、发电机、 汽车运动检测与控制的旋变数字转换器MS5905P
MS5905P 是一款 12bit 分辨率的旋变数字转换器。 片上集成正弦波激励电路,正弦和余弦允许输入峰峰值 幅度为 2.3V 到 4.0V ,可编程激励频率为 10kHz 、 12kHz 、 15kHz 、 20kHz 。 转换器可并行或串行输出角度 和速度对应的数字量。 MS5905…...
)
Ansible学习笔记(持续更新)
Ansible学习目录 1.自动化运维1.1 企业实际应用场景1.1.1 Dev开发环境1.1.2 测试环境1.1.3 发布环境1.1.4 生产环境1.1.5 灰度环境 1.2 程序发布1.3 自动化运维应用场景1.4 常用自动化运维工具 2.Ansible介绍和架构2.1 Ansible特性2.2 Ansible架构2.2.1 Ansible主要组成部分2.2…...

CCF HPC China2023|澎峰科技:使能先进计算,赋能行业应用
CCF HPC China2023圆满落幕! 桂秋八月,为期三天的中国高性能计算领域最高规格盛会——2023CCF全球高性能计算学术年会(HPC China)在青岛红岛国际展览中心圆满落幕。行业超算大咖、顶级学界精英、先锋企业领袖参会者齐聚山东青岛&a…...

【FlowDroid】一、处理流程学习
FlowDroid 一、处理流程学习 下载配置源码概况代码逻辑分析analyzeAPKFilerunInfoflowprocessEntryPointcalculateCallbacks(sourcesAndSinks)再次回到processEntryPoint 自己做一些笔记 下载配置 参照我前面的文章可以使用FlowDroid安装初体验 为了看代码了解FlowDroid如何处…...
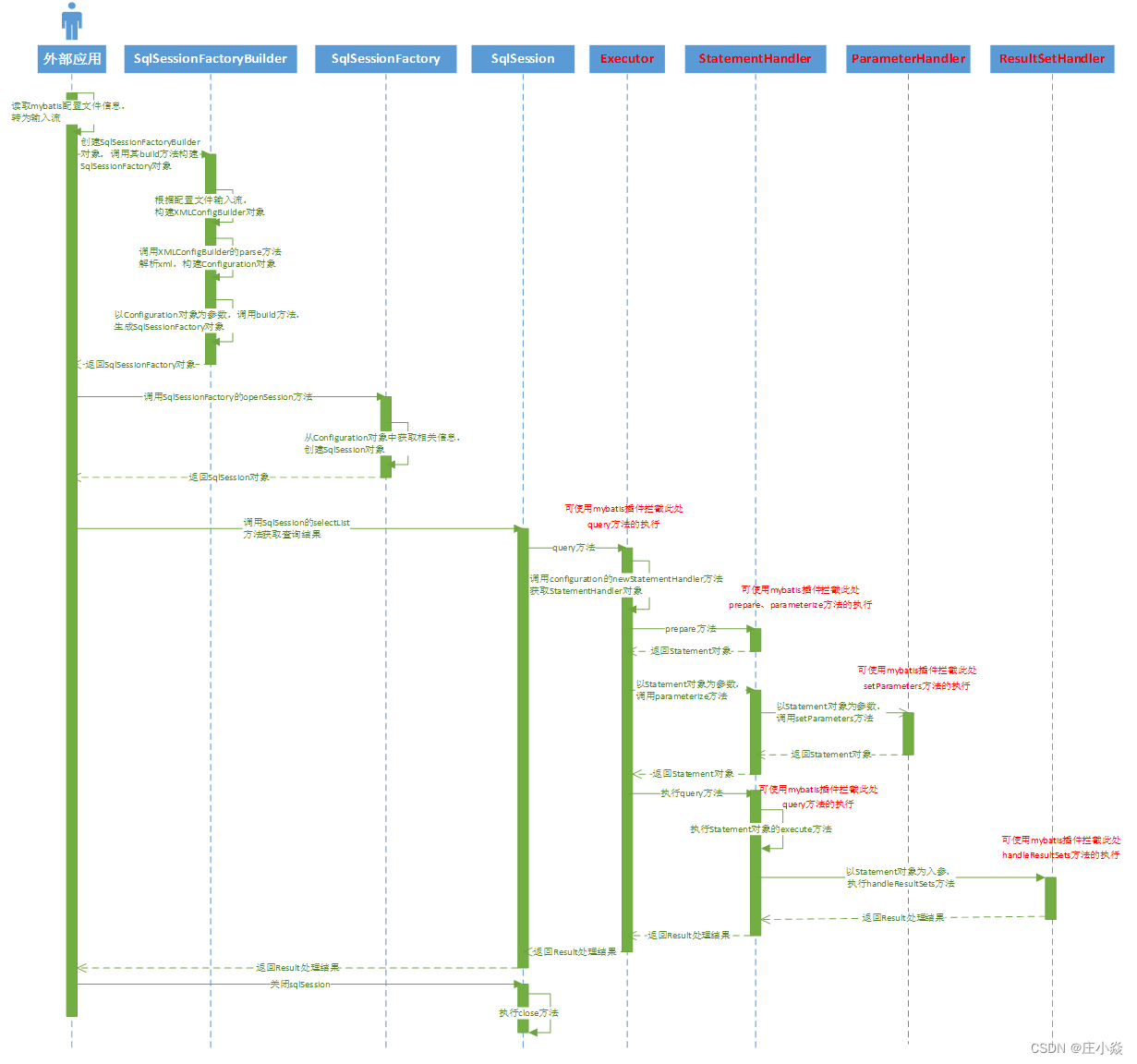
MyBatis——MyBatis插件原理
摘要 本博文主要介绍MyBatis插件机原理,帮助大家更好的理解和学习MyBatis。 一、插件机制概述 MyBatis 允许你在已映射语句执行过程中的某一点进行拦截调用。默认情况下,MyBatis允许使用插件来拦截的方法调用包括: Executor (update, que…...

简易虚拟培训系统-UI控件的应用5
目录 Toggle控件简介 示例-使用Toggle组实现主轴速度选择 本篇介绍UI控件Toggle,尝试一个小示例-使用单选框实现速度的选择控制。 Toggle控件简介 1. Toggle的结构如下:最重要的Toggle组件挂在Toggle节点上,下面的Image组件用于显示单选框…...
Lnmp架构
关闭防火墙 安装依赖包 yum -y install pcre-devel zlib-devel gcc gcc-c make 创建运行用户、组 编译安装Nginx 让系统识别nginx的操作命令 添加Nginx系统服务 vim /lib/systemd/system/nginx.service 编译安装mysql 安装Mysql环境依赖包 创建运行用户 编译安装 cd /opt …...
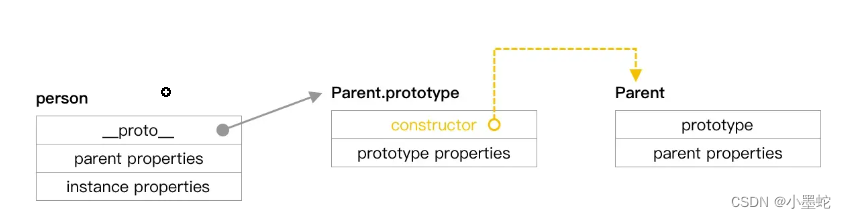
es5的实例__proto__(原型链) prototype(原型对象) {constructor:构造函数}
现在看这张图开始变得云里雾里,所以简单回顾一下 prototype 的基本内容,能够基本读懂这张图的脉络。 先介绍一个基本概念: function Person() {}Person.prototype.name KK;let person1 new Person();在上面的例子中, Person …...

Oracle DBlink使用方法
DBlink作用:在当前数据库中访问另一个数据库中的表中的数据 create public database link dblink名称 connect to 对方数据库用户名 identified by 对方数据库用户密码 using (DESCRIPTION (ADDRESS_LIST (ADDRESS (PROTOCOL TCP)(HOST 要连接的数据库所在服务…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...
