机器学习---决策树的划分依据(熵、信息增益、信息增益率、基尼值和基尼指数)
1. 熵
物理学上,熵 Entropy 是“混乱”程度的量度。

系统越有序,熵值越低;系统越混乱或者分散,熵值越⾼。
1948年⾹农提出了信息熵(Entropy)的概念。
从信息的完整性上进⾏的描述:当系统的有序状态⼀致时,数据越集中的地⽅熵值越⼩,数据
越分散的地⽅熵值越⼤。
从信息的有序性上进⾏的描述:当数据量⼀致时,系统越有序,熵值越低;系统越混乱或者分
散,熵值越⾼。
"信息熵" (information entropy)是度量样本集合纯度最常⽤的⼀种指标。 假定当前样本集合 D 中第
k 类样本所占的⽐例为 pk (k = 1, 2,. . . , |y|) ,![]() ,D为样本的所有数量,Ck 为第k类样本
,D为样本的所有数量,Ck 为第k类样本
的数量。 则 D 的信息熵定义为(log是以2为底,lg是以10为底):
 其中:Ent(D) 的值越⼩,则 D 的纯度越⾼。
其中:Ent(D) 的值越⼩,则 D 的纯度越⾼。
例子:假设我们没有看世界杯的⽐赛,但是想知道哪⽀球队会是冠军, 我们只能猜测某⽀球队是
或不是冠军,然后观众⽤对或不对来回答, 我们想要猜测次数尽可能少,⽤什么⽅法?
答案: ⼆分法。
假如有 16 ⽀球队,分别编号,先问是否在 1-8 之间,如果是就继续问是否在 1-4 之间, 以此类
推,直到最后判断出冠军球队是哪⽀。 如果球队数量是 16,我们需要问 4 次来得到最后的答案。
那么世界冠军这条消息的信息熵就是 4。
那么信息熵等于4,是如何进⾏计算的呢?
Ent(D) = -(p1 * logp1 + p2 * logp2 + ... + p16 * logp16),其中 p1, ..., p16 分别是这 16 ⽀球队
夺冠的概率。 当每⽀球队夺冠概率相等都是 1/16 的时侯,Ent(D) = -(16 * 1/16 * log1/16) = 4
每个事件概率相同时,熵最⼤,这件事越不确定。
2. 信息增益
信息增益:以某特征划分数据集前后的熵的差值。熵可以表示样本集合的不确定性,熵越⼤,样本
的不确定性就越⼤。 因此可以使⽤划分前后集合熵的差值来衡量使⽤当前特征对于样本集合D划分
效果的好坏。
信息增益 = entroy(前) - entroy(后)
信息增益表示得知特征X的信息⽽使得类Y的信息熵减少的程度。
假定离散属性a有 V 个可能的取值:
若使⽤ a 来对样本集 D 进⾏划分,则会产⽣ V 个分⽀结点,其中第v个分⽀结点包含了 D 中所有
在属性 a上取值为 av 的样本,记为 D。我们可根据前⾯给出的信息熵公式计算出 D 的信息熵,再
考虑到不同的分⽀结点所包含的样本数不同,给分⽀结点赋予权重![]()
即样本数越多的分⽀结点的影响越⼤,于是可计算出⽤属性 a 对样本集 D 进⾏划分所获得的"信息
增益" (information gain)。
其中:特征a对训练数据集 D 的信息增益 Gain(D,a),定义为集合 D 的信息熵 Ent(D) 与给定特征 a
条件下 D 的信息条件熵 Ent(D∣a) 之差,即公式为:

公式的详细解释: 信息熵的计算:
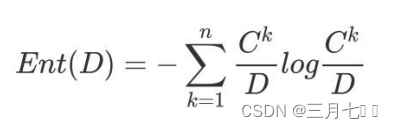
条件熵的计算:

其中:Dv 表示 a 属性中第 v 个分⽀节点包含的样本数
Ckv 表示 a 属性中第 v 个分⽀节点包含的样本数中,第 k 个类别下包含的样本数
⼀般⽽⾔,信息增益越⼤,则意味着使⽤属性 a 来进⾏划分所获得的"纯度提升"越⼤。因此,我们
可⽤信息增益来进⾏决策树的划分属性选择,著名的 ID3 决策树学习算法 [Quinlan, 1986] 就是
以信息增益为准则来选择划分属性。 其中,ID3 名字中的 ID 是 Iterative Dichotomiser (迭代⼆分
器)的简称。
比如:第⼀列为论坛号码,第⼆列为性别,第三列为活跃度,最后⼀列⽤户是否流失。 我们要解
决⼀个问题:性别和活跃度两个特征,哪个对⽤户流失影响更⼤?


通过计算信息增益可以解决这个问题,统计上右表信息。其中Positive为正样本(已流失),
Negative为负样本(未流失),下⾯的数值为不同划分下对应的⼈数。 可得到三个熵:
①计算类别信息熵(整体熵)

②性别属性的信息熵
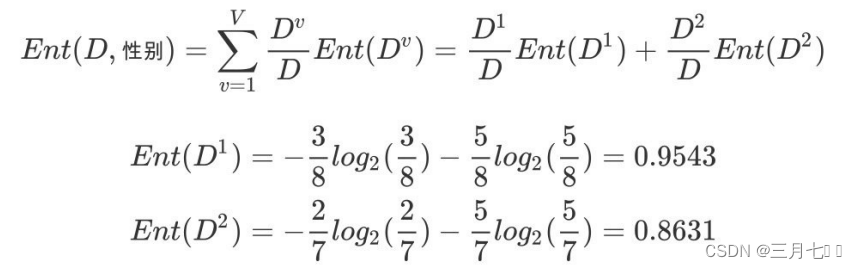
③性别的信息增益
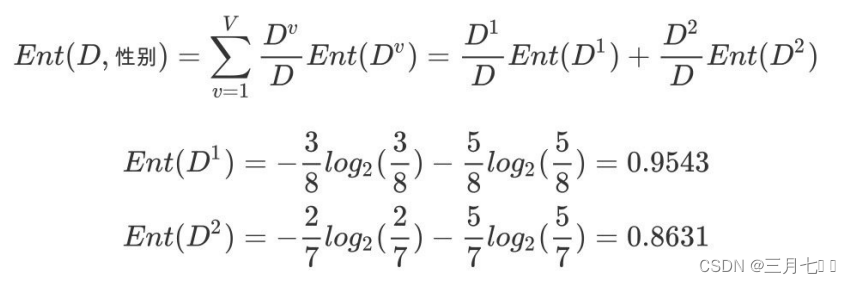
④活跃度的信息熵

⑤活跃度的信息增益
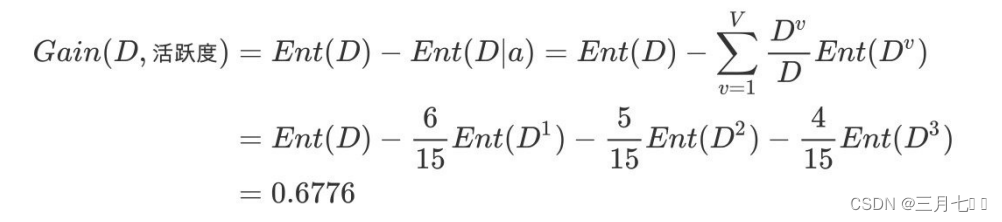
活跃度的信息增益⽐性别的信息增益⼤,也就是说,活跃度对⽤户流失的影响⽐性别⼤。在做特
征选择或者数据分析的时候,应该重点考察活跃度这个指标。
3. 信息增益率
在上⾯的介绍中,我们有意忽略了"编号"这⼀列。若把"编号"也作为⼀个候选划分属性,则根据信
息增益公式可计算出它的信息增益为 0.9182,远⼤于其他候选划分属性。 计算每个属性的信息熵
过程中,发现该属性的值为0,也就是其信息增益为0.9182。但是很明显这么分类,最后出现的结
果不具有泛化效果,⽆法对新样本进⾏有效预测。
实际上,信息增益准则对可取值数⽬较多的属性有所偏好,为减少这种偏好可能带来的不利影响,
著名的 C4.5 决策树算法不直接使⽤信息增益,⽽是使⽤"增益率" (gain ratio) 来选择最优划分属
性。 增益率:增益率是⽤前⾯的信息增益 Gain(D, a) 和属性 a 对应的"固有值"(intrinsic value) 的
⽐值来共同定义的。
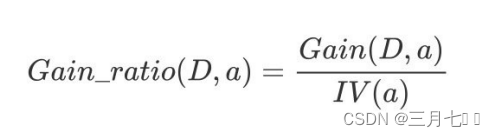
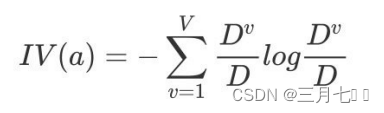
属性 a 的可能取值数⽬越多(即 V 越⼤),则 IV(a) 的值通常会越⼤。
⽤分裂信息度量来考虑某种属性进⾏分裂时分⽀的数量信息和尺⼨信息,把这些信息称为属性的内
在信息 (instrisic information)。信息增益率⽤信息增益/内在信息,会导致属性的重要性随着内在
信息的增⼤⽽减⼩(也就是说,如果这个属性本身不确定性就很⼤,那我就越不倾向于选取它),
这样算是对单纯⽤信息增益有所补偿。
上面的例子中,计算属性分裂信息度量:
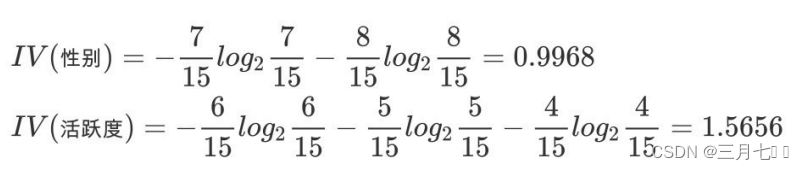
计算信息增益率:

活跃度的信息增益率更⾼⼀些,所以在构建决策树的时候,优先选择通过这种⽅式,在选取节点的
过程中,我们可以降低取值较多的属性的选取偏好。
例子2:第⼀列为天⽓,第⼆列为温度,第三列为湿度,第四列为⻛速,最后⼀列该活动是否进
⾏。根据下⾯表格数据,判断在对应天⽓下,活动是否会进⾏?


该数据集有四个属性,属性集合A={ 天⽓,温度,湿度,⻛速}, 类别标签有两个,类别集合L={进
⾏,取消}。
①计算类别信息熵。类别信息熵表示的是所有样本中各种类别出现的不确定性之和。根据熵的概
念,熵越⼤,不确定性就越⼤,把事情搞清楚所需要的信息量就越多。

②计算每个属性的信息熵。每个属性的信息熵相当于⼀种条件熵。表示的是在某种属性的条件下,
各种类别出现的不确定性之和。属性的信息熵越⼤,表示这个属性中拥有的样本类别越不“纯”。

③计算信息增益。信息增益 = 熵 - 条件熵,在这⾥就是类别信息熵 - 属性信息熵,它表示的是信息
不确定性减少的程度。如果⼀个属性的信息增益越⼤,就表示⽤这个属性进⾏样本划分可以更好的
减少划分后样本的不确定性,当然,选择该属性就可以更快更好地完成分类⽬标。 信息增益就是
ID3算法的特征选择指标。

假设把上⾯表格1的数据前⾯添加⼀列为"编号",取值(1--14)。若把"编号"也作为⼀个候选划分属
性,则根据前⾯步骤:计算每个属性的信息熵过程中,该属性的值为0,也就是其信息增益为
0.940。但是很明显这么分类,最后出现的结果不具有泛化效果。此时根据信息增益就⽆法选择出
有效分类特征。所以,C4.5选择使⽤信息增益率对ID3进⾏改进。
④计算属性分裂信息度量。⽤分裂信息度量来考虑某种属性进⾏分裂时分⽀的数量信息和尺⼨信
息,把这些信息称为属性的内在信息 (instrisic information)。信息增益率⽤信息增益/内在信息,
会导致属性的重要性随着内在信息的增⼤⽽减⼩(也就是说,如果这个属性本身不确定性就很⼤,
那就越不倾向于选取它),这样算是对单纯⽤信息增益有所补偿。
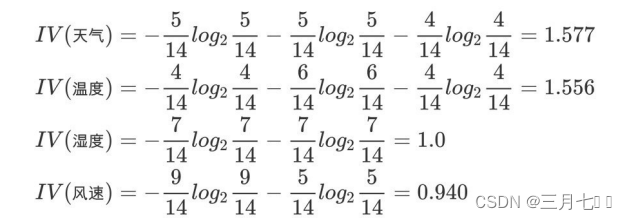
⑤计算信息增益率。

天⽓的信息增益率最⾼,选择天⽓为分裂属性。发现分裂了之后,天⽓是“阴”的条件下,类别是”纯
“的,所以把它定义为叶⼦节点,选择不“纯”的结点继续分裂。
C4.5的算法流程:
while(当前节点"不纯"):1.计算当前节点的类别熵(以类别取值计算)2.计算当前阶段的属性熵(按照属性取值吓得类别取值计算)3.计算信息增益4.计算各个属性的分裂信息度量5.计算各个属性的信息增益率
end while
当前阶段设置为叶⼦节点C4.5的优点:
①⽤信息增益率来选择属性,克服了⽤信息增益来选择属性时偏向选择值多的属性的不⾜。
②采⽤了⼀种后剪枝⽅法避免树的⾼度⽆节制的增⻓,避免过度拟合数据
③对于缺失值的处理 在某些情况下,可供使⽤的数据可能缺少某些属性的值。假如〈x,c(x)〉是
样本集S中的⼀个训练实例,但是其属性A 的值A(x)未知。 处理缺少属性值的⼀种策略是赋给它结
点n所对应的训练实例中该属性的最常⻅值; 另外⼀种更复杂的策略是为A的每个可能值赋予⼀个
概率,C4.5就是使⽤这种⽅法处理缺少的属性值。
4. 基尼值和基尼指数
CART 决策树 [Breiman et al., 1984] 使⽤"基尼指数"(Gini index)来选择划分属性。CART 是
Classification and Regression Tree的简称,这是⼀种著名的决策树学习算法,分类和回归任务都
可⽤基尼值Gini(D):从数据集D中随机抽取两个样本,其类别标记不⼀致的概率。Gini(D)值
越⼩,数据集D的纯度越⾼。 数据集 D 的纯度可⽤基尼值来度量:

![]() D为样本的所有数量,Ck 为第 k 类样本的数量。
D为样本的所有数量,Ck 为第 k 类样本的数量。
基尼指数Gini_index(D):⼀般,选择使划分后基尼系数最⼩的属性作为最优化分属性。
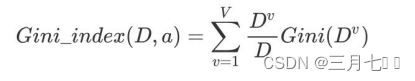
1. 对数据集⾮序列标号属性{是否有房,婚姻状况,年收⼊}分别计算它们的Gini指数,取Gini指数
最⼩的属性作为决策树的根节点属性。
2. 根节点的Gini值为:
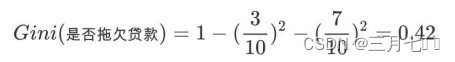
3. 当根据是否有房来进⾏划分时,Gini指数计算过程为:

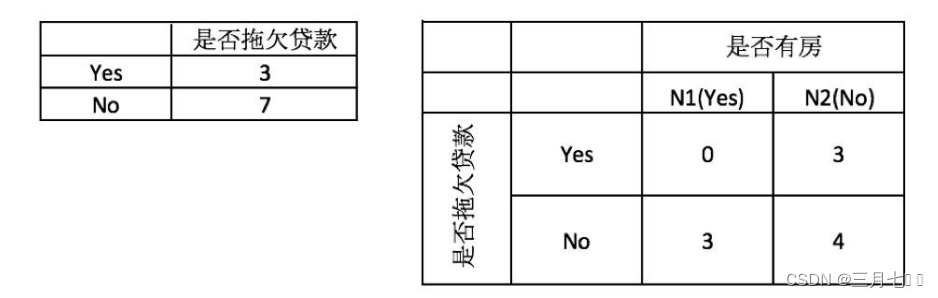
4. 若按婚姻状况属性来划分,属性婚姻状况有三个可能的取值{married,single,divorced},分别
计算划分后的Gini系数增益。 {married} | {single,divorced} {single} | {married,divorced} {divorced} |
{single,married}

对⽐计算结果,根据婚姻状况属性来划分根节点时取Gini指数最⼩的分组作为划分结果,即:
{married} | {single,divorced} 。
5. 同理可得年收⼊Gini: 对于年收⼊属性为数值型属性,⾸先需要对数据按升序排序,然后从⼩
到⼤依次⽤相邻值的中间值作为分隔将样本划分为两组。例如当⾯对年收⼊为60和70这两个值
时,我们算得其中间值为65。以中间值65作为分割点求出Gini指数。


根据计算知道,三个属性划分根节点的指数最⼩的有两个:年收⼊属性和婚姻状况,他们的指数都
为0.3。此时,选取⾸先出现的属性{married}作为第⼀次划分。
6. 接下来,采⽤同样的⽅法,分别计算剩下属性,其中根节点的Gini系数为(此时是否拖⽋贷款的
各有3个records)。
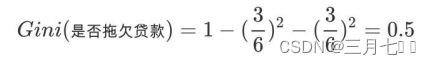
7. 对于是否有房属性,可得:
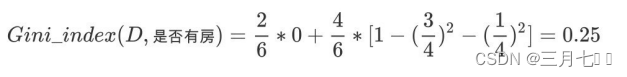
8. 对于年收⼊属性则有:

经过如上流程,构建的决策树,如下图:
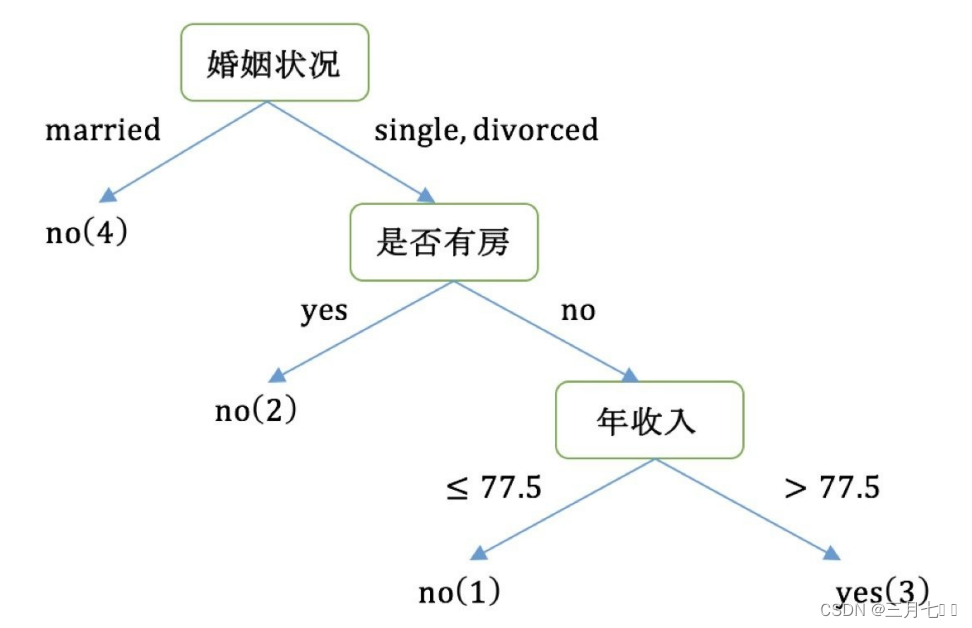
CART的算法流程:
while(当前节点"不纯"):1.遍历每个变量的每⼀种分割⽅式,找到最好的分割点2.分割成两个节点N1和N2
end while
每个节点⾜够“纯”为⽌
相关文章:

机器学习---决策树的划分依据(熵、信息增益、信息增益率、基尼值和基尼指数)
1. 熵 物理学上,熵 Entropy 是“混乱”程度的量度。 系统越有序,熵值越低;系统越混乱或者分散,熵值越⾼。 1948年⾹农提出了信息熵(Entropy)的概念。 从信息的完整性上进⾏的描述:当系统的有序…...

java解析json
1. 解析根节点为“{}”的json {"id": 1525490,"name": "有缘网" }代码: String jsonString "{\"id\":1525490\",\"name\":\"有缘网\"}";JSONObject jsonObject JSONObject.…...

PAT 1163 Dijkstra Sequence
个人学习记录,代码难免不尽人意。 Dijkstra’s algorithm is one of the very famous greedy algorithms. It is used for solving the single source shortest path problem which gives the shortest paths from one particular source vertex to all the other v…...
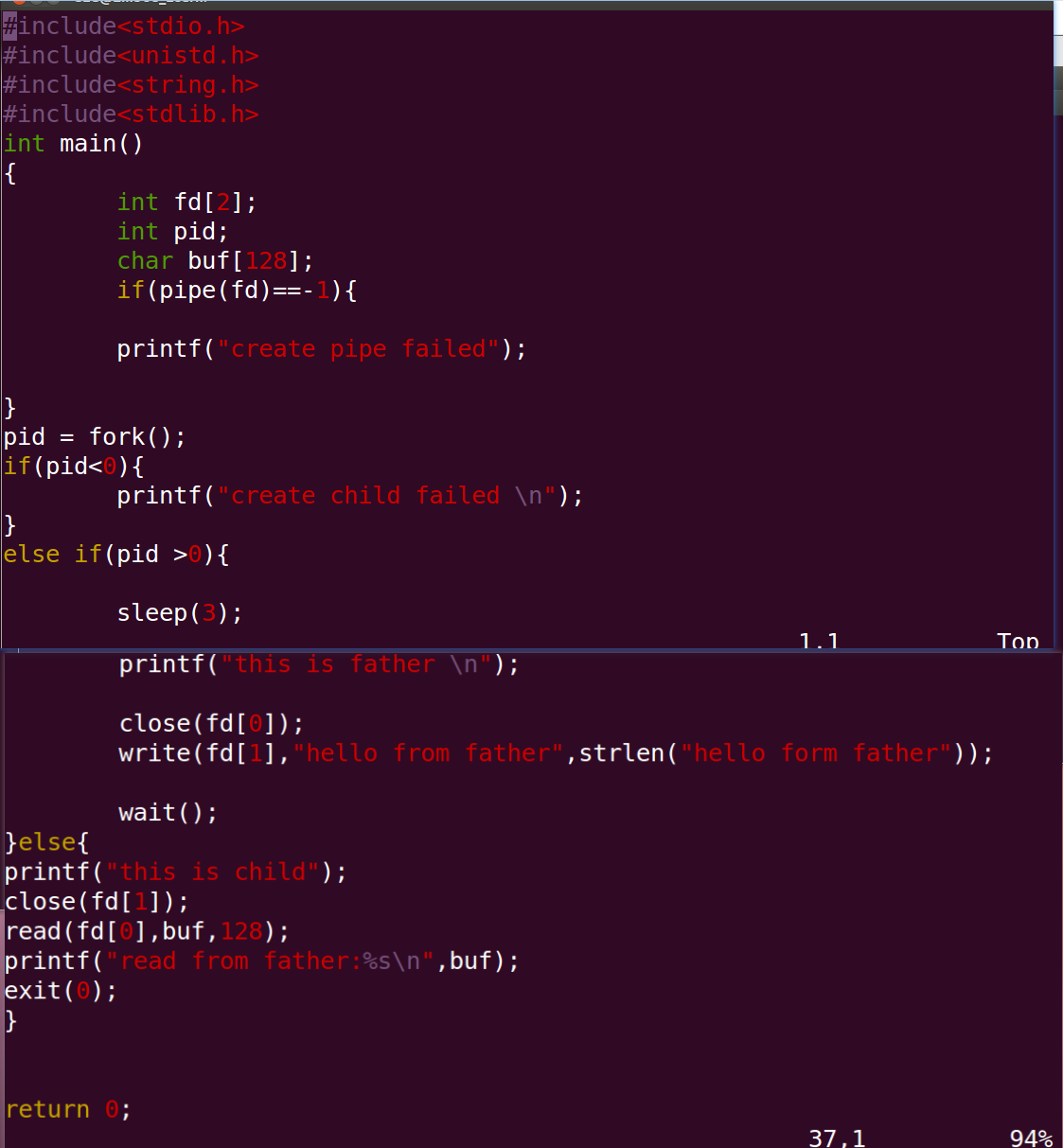
嵌入式学习之进程
1.进程间通信概述 UNIX系统IPC是各种进程通信方式的统称。 2.管道通信原理 特点: 1.它是半双工的(即数据只能在一个方向上流动),具有固定的读端和写端。 2.它只能用于具有亲缘关系的进程之间通信(也是父子进程或者…...

C#-单例模式
文章目录 单例模式的概述为什么会有单例模式如何创建单例模式1、首先要保证,该对象 有且仅有一个2、其次,需要让外部能够获取到这个对象 示例通过 属性 获取单例 单例模式的概述 总结来说: 单例 就是只有 一个实例对象。 模式 说的是设计模式…...

WSNs 安全技术
WSNs 多用于军事,特殊现场的警戒保护、商业区域的安防,作为任务型网 络,不仅要进行数据传输,而且要进行数据采集和融合,任务的协同控制等,如何 保证任务执行的机密性,数据产生的可靠性数据融合…...

H5如何做页面下拉刷新和上拉加载
这里以vant为例 结构 <van-pull-refreshv-model"isLoading"success-text"刷新成功"refresh"onRefresh"><van-liststyle"height:100%"v-model"loading":finished"finished"finished-text"没有更多了…...

Camunda 7.x 系列【42】事件子流程
有道无术,术尚可求,有术无道,止于术。 本系列Spring Boot 版本 2.7.9 本系列Camunda 版本 7.19.0 源码地址:https://gitee.com/pearl-organization/camunda-study-demo 文章目录 1. 概述2. 案例演示2.1 流程模型2.2 测试1. 概述 事件子流程是由事件触发的子流程,可存在…...
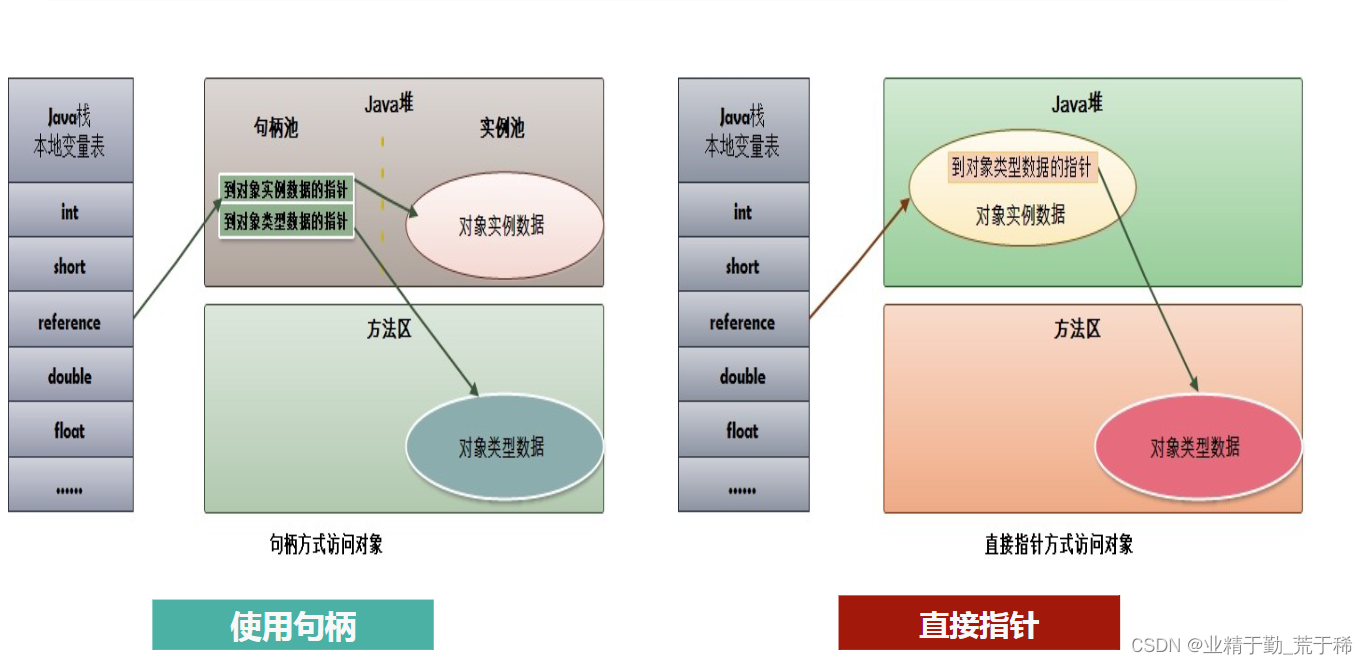
JVM类的加载过程
加载过程 JVM的类的加载过程分为五个阶段:加载、验证、准备、解析、初始化。 加载 加载阶段就是将编译好的的class文件通过字节流的方式从硬盘或者通过网络加载到JVM虚拟机当中来。(我们平时在Idea中书写的代码就是放在磁盘中的,也可以通…...
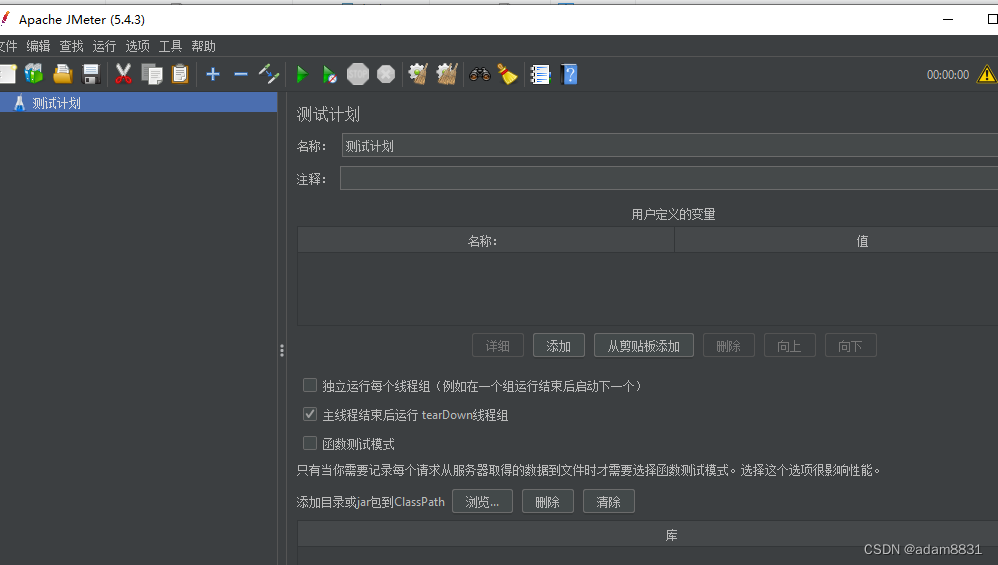
Jmeter如何设置中文版
第一步:找到 apache-jmeter-5.4.3\bin目录下的 jmeter.properties 第二步:打开 三,ctrf 输入languageen,注释掉,增加以行修改如下 四,ctrs 保存修改内容,重新打开jmeter就可以了...
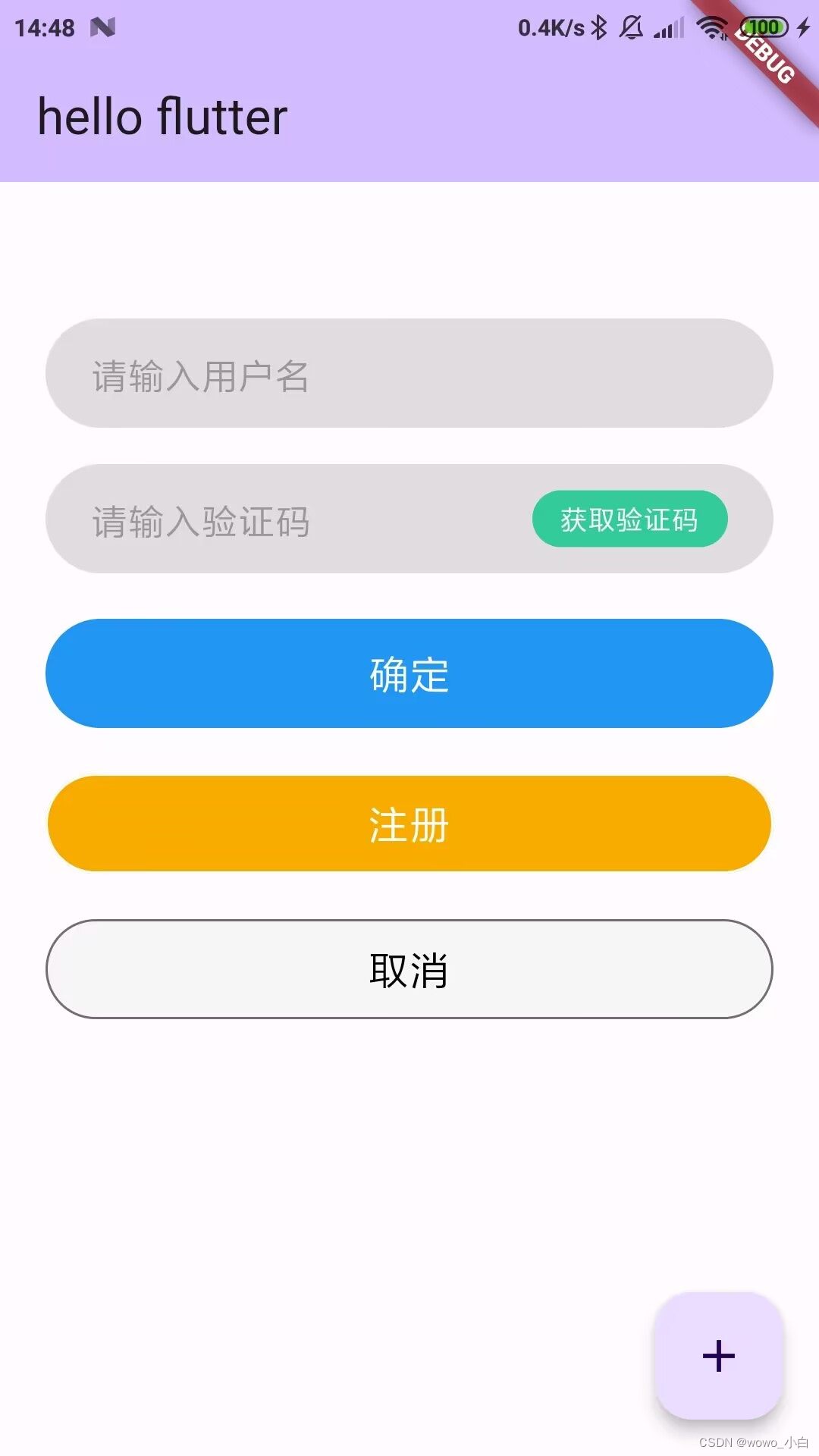
flutter自定义按钮-文本按钮
目录 前言 需求 实现 前言 最近闲着无聊学习了flutter的一下知识,发现flutter和安卓之间,页面开发的方式还是有较大的差异的,众所周知,android的页面开发都是写在xml文件中的,而flutter直接写在代码里(da…...

无涯教程-Android - CheckBox函数
CheckBox是可以由用户切换的on/off开关。为用户提供一组互不排斥的可选选项时,应使用复选框。 CheckBox 复选框属性 以下是与CheckBox控件相关的重要属性。您可以查看Android官方文档以获取属性的完整列表以及可以在运行时更改这些属性的相关方法。 继承自 android.widget.T…...

[Go版]算法通关村第十五关青铜——用4KB内存寻找重复元素
目录 题目:用4KB内存寻找重复元素思路分析:使用位存储如何存储这32000个整数?每个整数对应在位图中的存储状态举例如何判断是重复的?具体的步骤 复杂度:时间复杂度 O ( n ) O(n) O(n)、空间复杂度 O ( 1 ) O(1) O(1)Go…...

OJ练习第159题——消灭怪物的最大数量
消灭怪物的最大数量 力扣链接:1921. 消灭怪物的最大数量 题目描述 你正在玩一款电子游戏,在游戏中你需要保护城市免受怪物侵袭。给你一个 下标从 0 开始 且长度为 n 的整数数组 dist ,其中 dist[i] 是第 i 个怪物与城市的 初始距离&#…...
)
Prometheus-Rules(规则)
文章目录 一、介绍二、配置 Prometheus 使用规则文件三、 规则文件语法规则文件语法全局Recording rules(记录规则)2 Alerting rules(警报规则)3 模板化如何使用四、检查规则文件语法五、发送警报通知一、介绍 Prometheus规则是一种逻辑表达式,可用于定义有关监控数据的逻…...
打卡智能中国(六):村里出了“飞行员”
提起返乡青年,你的第一印象是什么?失败、躺平、卷不动了? 我们在浙江、福建、青海等地,参观一些农业智能化项目时,陪同参观的“飞手”,高兴地跟我们分享自己的心路历程: 在家门口做农业无人机操…...

自动化运维工具Ansible之playbooks剧本
自动化运维工具Ansible之playbooks剧本 一、playbooks1.playbooks简述2.playbooks剧本格式3.playbooks组成部分 二、实例1.编写脚本2.运行playbook3.定义、引用变量4.指定远程主机sudo切换用户5.when条件判断6.迭代7.Templates 模块8.tags 模块9.Roles 模块 三、编写应用模块1.…...
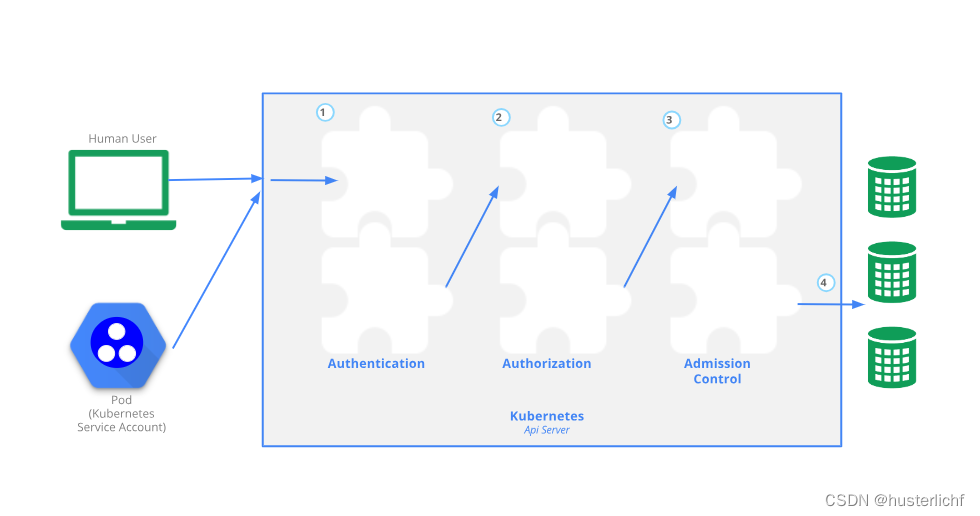
K8S访问控制------认证(authentication )、授权(authorization )、准入控制(admission control )体系
一、账号分类 在K8S体系中有两种账号类型:User accounts(用户账号),即针对human user的;Service accounts(服务账号),即针对pod的。这两种账号都可以访问 API server,都需要经历认证、授权、准入控制等步骤,相关逻辑图如下所示: 二、authentication (认证) 在…...

开开心心带你学习MySQL数据库之第三篇上
学校的项目组有必要加入吗? 看你的初心. ~~如果初心是通过这个经历能够提高自己的技术水平 ~~是可以考虑的 ~~如果初心是通过这个经历提高自己找工作的概率 ~~这个是不靠谱的,啥用没有 ~~如果初心是通过这个体验更美好的大学生活 ~~靠谱的 秋招,应届生,找工作是非常容易的!!! …...
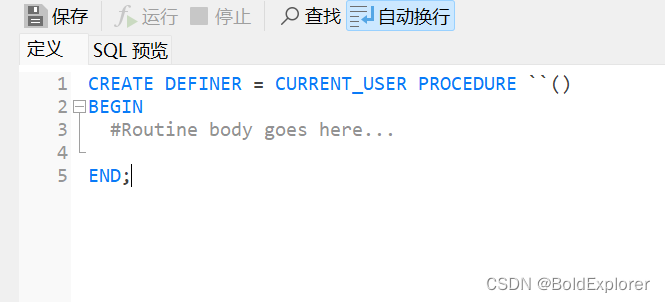
Mysql批量插入大量数据的方法
使用存储过程进行插入, 在navicate中示例如下: 输入需要的参数点击完成 在begin end中输入代码,示例代码如下 CREATE DEFINERskip-grants userskip-grants host PROCEDURE batch_insert() BEGINdeclare i int default 0; set i0;while i<1…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...
