24.排序,插入排序,交换排序
目录
一. 插入排序
(1)直接插入排序
(2)折半插入排序
(3)希尔排序
二. 交换排序
(1)冒泡排序
(2)快速排序
排序:将一组杂乱无章的数据按一定规律顺次排列起来。即,将无序序列排成一个有序序列(由小到大或由大到小)的运算。如果参加排序的数据结点包含多个数据域,那么排序往往是针对其中某个域而言。
排序方法:
- 按数据存储介质:内部排序和外部排序
- 按比较器个数:串行排序和并行排序
- 按主要操作:比较排序和基数排序(后面会讲)
- 按辅助空间:原地排序和非原地排序
- 按稳定性:稳定排序和非稳定排序
- 按自然性:自然排序和非自然排序
本章学习内容:
- 插入排序:直接插入排序、折半插入排序、希尔排序
- 交换排序:冒泡排序、快速排序
- 选择排序:简单选择排序、堆排序
- 归并排序:2-路归并排序
- 基数排序
衡量排序算法的指标有时间复杂度,空间复杂度和稳定性等。对于稳定性做一点说明。稳定排序指的是能够使任何数值相等的元素,排序以后相对次序不变。例如,下面的示例1是稳定排序,示例2就不是稳定排序。
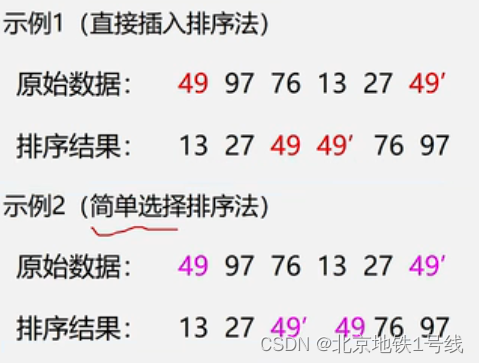
排序的稳定牲只对结构类型数据排序有意义。例如:n个学生信息(学号、姓名、语文、数学、英语、总分),首先按数学成绩从高到低排序,然后按照总分从高到低排序。若是稳定排序,总分相同的情况下,数学成绩高的仍然排在前面。
存储结构:本章基于的存储结构均以顺序表存储。
#define MAXSIZE 20 //设记录不超过20个
typedef int KeyType; //设关键字为整型量(int型)typedef struct{ //定义每个记录(数据元素)的结构KeyType key; //关键字InfoType otherinfo; //其它数据项
}RedType; //Record Typetypedef struct{ //定义顺序表的结构RedType r[MAXSIZE+1]; //存储顺序表的向量//r[0]一般作哨兵或缓冲区int length; //顺序表的长度
}SqList;
一. 插入排序
基本思想:每步将一个待排序的对象,按其关键码大小,插入到前面已经排好序的一组对象的适当位置上,直到对象全部插入为止。即边插入边排序。
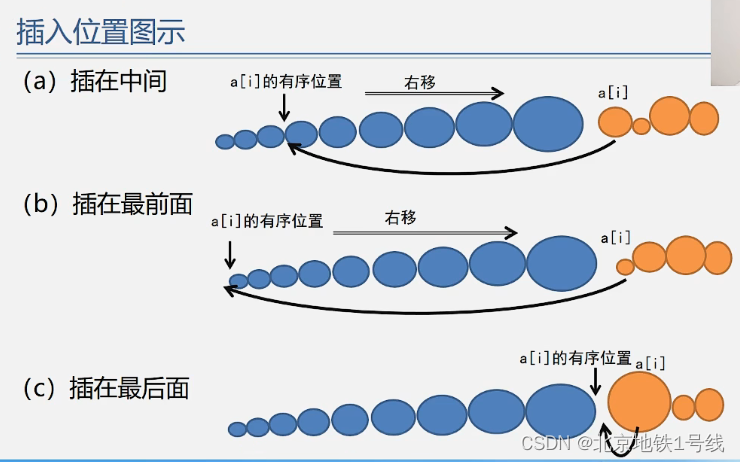
根据确定插入位置的方法不同,我们可以有以下三种插入排序的方法:
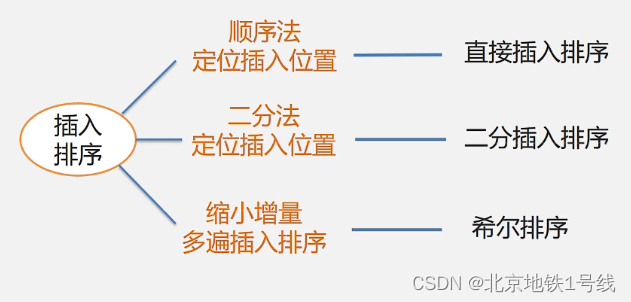
(1)直接插入排序
顺序法定位插入位置:一个一个比较。
- 首先,复制待插入的元素,复制插入元素。x=a[i];
- 然后,记录后移,查找插入位置;for(j=i-1; j>=0&&x<a[j];j--),a[j+1]=a[j];
- 最后,插入到正确位置,a[j+1]=x;
对于复制待插入的元素,我们可以使用哨兵。把待插入的元素复制到0号位,这样省去了越界的判断:
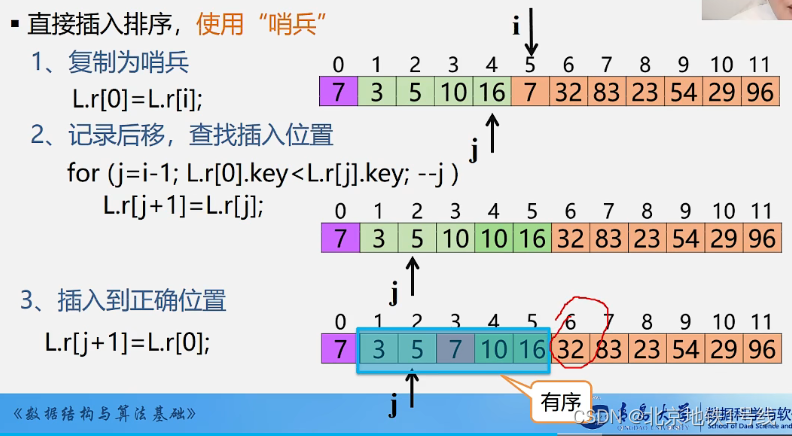
此外,如果待插入元素比有序表最后一位还大,那就不用进行任何操作了,这个位置就是待插入元素的位置。
void InsertSort(SqList &L){int i, j;for(i=2; i<=L.length; ++i){ //第1个元素不用排序,从插入第2个元素开始if (L.r[i].key < L.r[i-1].key){ //若"<",需将L.r[i]插入有序子表L.r[0]=L.r[i]; //复制为哨兵for(j=i-1; L.r[0].key<L.r[j].key; --j){L.r[j+1]=L.r[j]; //记录后移}L.r[j+1]=L.r[0]; //插入到正确位置}}
}
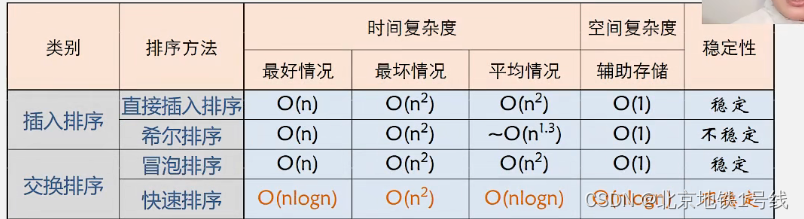
下面我们来分析时间效率。实现排序的基本操作有两个:(1)“比较”序列中两个关键字的大小;(2)“移动”记录。最好的情况是,关键字在记录序列中顺序有序。这时比较的次数是,不需要移动。最坏的情况是,关键字在记录序列中逆序有序。这时比较的次数是
,移动的次数是
,从而我们可以得到以下结论:
- 原始数据越接近有序,排序速度越快;
- 最坏情况下(输入数据是逆有序的)Tw(n)=O(n^2);
- 平均情况下,耗时差不多是最坏情况的一半Te(n)=O(n^2);
- 空间复杂度是O(1);
- 要提高查找速度,可以从减少元素的比较次数和减少元素的移动次数入手;
(2)折半插入排序
查找插入位置采用折半查找法。
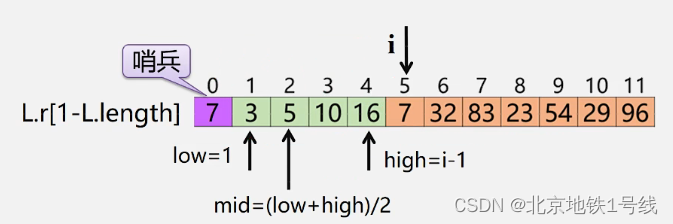
void BlnsertSort (SqList &L){for (i = 2; i<= L.length ; ++i){ //依次插入第2~第n个元素L.r[0] = L.r[i]; //当前插入元素存到“哨兵”位置low = 1 ; high = i-1; //采用二分查找法查找插入位置while (low <= high){mid = (low + high)/2;if (L.r[0].key < L.r[mid].key) high = mid-1;else low = mid + 1;} //循环结束,high+1则为插入位置for (j=i-1; j>=high+1; --j) L.r[j+1] = L.r[j]; //移动元素L.r[high+1] = L.r[0]; //插入到正确位置
}// BInsertSort
最后我们分析算法的时间效率。折半查找比顺序查找快,所以折半插入排序就平均性能来说比直按插入排序要快。它所需要的关键码比较次数与待排序对象序列的初始排列无关,仅依赖于对象个数。在插入第i个对象时,需要经过次关键码比较,才能确定它应插入的位置。
当n较大时,总关键码比较次数比直接插入排序的最坏情况要好得多,但比其最好情况要差。在对象的初始排列已经按关键码排好序或接近有序时,直接插入排序比折半插入排序执行的关键码比较次数要少。对移动次数,折半插入排序的对象移动次数与直接插入排序相同,依赖于对象的初始排列。所以折半插入排序减少了比较次数,但没有减少移动次数。平均性能优于直接插入排序。其时间复杂度为O(n^2),空间复杂度是O(1),是一种稳定的排序方法。
(3)希尔排序
直接排序什么时候效率较高?一是序列基本有序,二是序列长度较小。基于此我们提出希尔排序的基本思路:先将整个待排记录序列分割成若干子序列,分别进行直接插入排序,待整个序列中的记录“基本有序”时,再对全体记录进行一次直接插入排序。希尔排序的算法特点是:
- 一次移动,移动位置较大,跳跃式地接近排序后的最终位置
- 最后一次只需要少量移动
- 增量序列必须是递减的,最后一个必须是1
- 增量序列应该是互质的
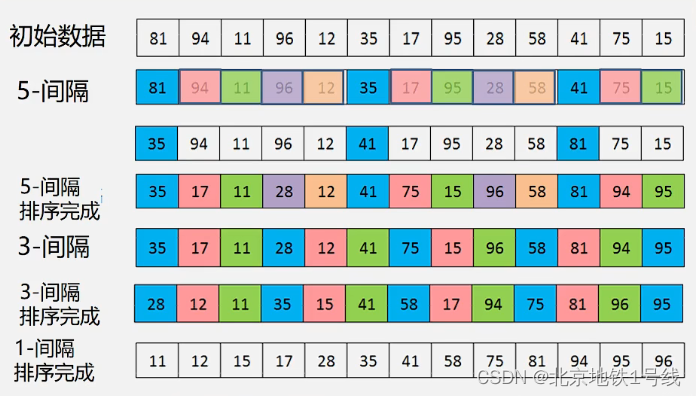
首先:定义增量序列,刚才的例子中
然后:对每个进行“
-间隔”插入排序(k=M,M-1,...1)。
//主程序
void ShellSort(Sqlist &L,int dlta[],int t){//按增量序列dlta[0..t-1]对顺序表L作希尔排序,t是增量序列的长度for(k=O; k<t; ++k)Shellnsert(L,dlta[k]); //一趟增量为dlta[k]的插入排序
}//ShellSortvoid ShellInsert(SqList &L,int dk){ //对顺序表L进行一趟增量为dk的Shell排序,dk为步长因子//和一趟直接插入排序相比,做了以下修改://1.前后记录位置的增量是dk,不是1//2.r[0]只是暂存单元,不是哨兵,当j<=0时,插入位置已找到for(i = dk+1; i <= L.length; ++i) //dk间隔排序,从dk+1开始排序,例如前面讲的一趟直接插入排序从第2个元素开始排序if(r[i].key < r[i-dk].key){ //比前面的大则不需要执行插入操作L.r[0] = L.r[i]; //暂存在L.r[0]for(j = i-dk; j>0 &&(r[0].key < r[j].key); j = j-dk)r[j+dk]=r[j]; //后移L.r[j+dk]=L.r[0]; //插入,退出循环时r[j]<r[0],所以插到L.r[j+dk]的位置}
}
希尔排序的算法效率与增量序列的取值有关。
对于Hibbard增量序列,,相邻元素互质。最坏情况
;猜想:
;
Sedgewick增量序列{1,5,19,41,109...},或
。猜想:
,
;
希尔排序法是一种不稳定的排序算法,例如对下面d=2的情况:

总结:对希尔排序来说,时间复杂度是n和d的函数,空间复杂度是O(1),是一种不稳定的排序方法。关于如何选择最佳d序列,目前尚未有解决方案。但是,最后一个增量值必须为1,其他序列元素之间无除了1之外的公因子。此外,希尔排序不宜在链式存储结构上实现。
二. 交换排序
基本思想:两两比较,如果发生逆序则交换,直到所有记录都排好序为止。
常见的交换排序方法:冒泡排序,快速排序。
(1)冒泡排序
给定初始序列:21,25,49,25*,16,08,n=6。
第1趟:
位置0,1进行比较——判断——不交换——结果:21,25,49,25*,16,08
位置1,2进行比较——判断——不交换——结果:21,25,49,25*,16,08
位置2,3进行比较——判断——交换——结果:21,25,25*,49,16,08
位置3,4进行比较——判断——交换——结果:21,25,25*,16,49,08
位置4,5进行比较——判断——交换——结果:21,25,25*,16,08,49
第1趟结束后:21,25,25*,16,08,49
第2趟:
位置0,1进行比较——判断——不交换——结果:21,25,25*,16,08,49
位置1,2进行比较——判断——不交换——结果:21,25,25*,16,08,49
位置2,3进行比较——判断——交换——结果:21,25,16,25*,08,49
位置3,4进行比较——判断——交换——结果:21,25,16,08,25*,49
第2趟结束后:21,25,16,08,25*,49
继续下一趟,每一趟增加一个有序元素。
第3趟结果:21,16,08,25,25*,49
第4趟结果:16,08,21,25,25*,49
第5趟结果:08,16,21,25,25*,49
总结:n个记录,需要比较n-1趟。第m趟需要比较n-m次。
void bubble_sort(SqList &L){ //冒泡排序算法int m,i,j; RedType x; //交换时临时存储for(m=1; m<=n-1; m++){ //总共需n-1趟for(j=1; j<=n-m; j++) //第m趟需要比较n-m次if(L.r[j].key > L.r[j+1].key){ //发生逆序x=L.r[j]; L.r[j]=L.r[j+1]; L.r[j+1]=x; //交换}//endif}//for
}
冒泡排序的优点:每趟结束时,不仅能挤出一个最大值到最后面位置,还能同的部力理顺其他元素。实际上,一旦某一趟比较时不出现记录交换,说明已排好序了,就可以结束本算法。所以我们可以增设一个标识flag:
void bubble_sort(SqList &L){ //改进的冒泡排序算法int m,i,j;flag=1; //flag作为是否有交换的标记RedType x; for(m=1; m<=n-1 && flag==1; m++){flag=0;for(j=1; j<=n-m; j++){if(L.r[j].key>L.r[j+1].key){//发生逆序flag=1; //发生交换,flag置为1,若本趟没发生交换,flag保持为零x=L.r[j]; L.r[j]=L.r[j+1]; L.r[j+1]=x; //交换}//endif}//for}
}
下面分析时间复杂度。最好情况是全为正序,这时比较次数是n-1,移动的次数是0;最坏情况是全为逆序,比较次数是,移动次数是
(包含向中间辅助变量x移动)。所以,冒泡排序最好时间复杂度是O(n),最坏时间复杂度为O(n^2),平均时间复杂度为O(n^2)。冒泡排序算法中增加一个辅助空间temp,辅助空间为S(n)=O(1),冒泡排序是稳定的排序算法。
(2)快速排序
快速排序是一种改进的交换排序。基本思想是递归思想:任取一个元素(如:第一个)为中心pivot,所有比它小的元素一律前放,比它大的元素一律后放,形成左右两个子表。对各子表重新选择中心元素并依此规则调整,直到每个子表的元素只剩一个(结束条件)。下面的过程,每个表中都选取第一个作为中心点(分界点)。
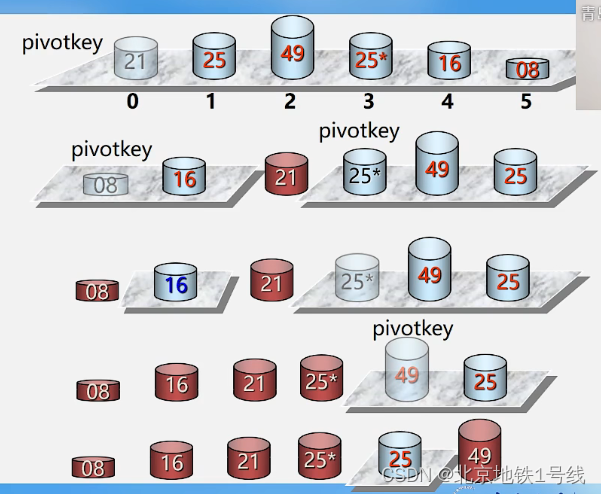
例如:给定序列

序列共8个数,界点直接取第一个数49,并把它搬到0号位。指针low=1,high=8.由于第1个位置已空,我们从后往前移动high,找一个小于界点的数把它搬到1号位。high--,当high=7的时候,数27满足,把27搬到1号位。此时7位空出来,我们向后移动low,找一个大于界点的数搬到空出来的7号位。low++,当low=3的时候,数65满足,把65搬到7号位,此时3号位空出来。我们再往前移动high,找一个大于界点的数搬到3号位。当high=6,数字13符合,13搬到3号位,6号位又空出。继续往后移动low,low=4,数97符合,97搬到6号位,4号位空出。然后往前移动high,high=5没有符合题意的,继续向前移动至high=4,此时high与low都重合。再把界点49填到4号位。此时8个数字的表就能以4号位49为界分成两个子表:前面1-3位,后面5-8位。然后在对两个子表分别执行相同的操作。
总结:①每一趟的子表的形成是采用从两头向中间交替式逼近法;②由于每趟中对各子表的操作都相似,可采用递归算法。
void main(){QSort(L, 1, L.length);
}void QSort(SqList &L, int low, int high){ //对顺序表L快速排序if(low < high){ //长度大于1pivotloc = Partition(L, low, high);//将L一分为二,pivotloc为中心点元素排好序的位置QSort(L, low, pivotloc-1); //对低子表递归排序QSort(L, pivotloc+1, high); //对高子表递归排序}//end if
}//QSortint Partition(SqList &L, int low, int high){L.r[0] = L.r[low]; //取[low,high]的第一个元素作为中心点,并搬前面去 pivotkey = L.r[low].key; //这里也是取中心点while (low < high){ //循环终止的条件是low=highwhile (low < high && L.r[high].key >= pivotkey) --high; //low指针指的地方空出,前移high,直到找到一个小于pivotkey的L.r[low] = L.r[high]; //然后搬到空出的地方low,此时high又空出来while (low < high && L.r[low].key <= pivotkey) ++low; //high指针指的地方空出,后移low,直到找到一个大于pivotkey的L.r[high] = L.r[low]; //然后搬到空出的地方high,此时low又空出来}L.r[low]=L.r[0]; //退出循环,再把最后指针重合的地方就是空的地方,填回中心点return low; //返回中心点所在的位置
}下面分析算法效率:可以证明,时间复杂度是,其中对上面的Qsort()是
,对下面的Partition()是
。实验结果表明:就平均计算时间而言,快速排序是我们所讨论的所有内排序方法中最好的一个。
接下来分析空间复杂度:快速排序不是原地排序。由于程序中使用了递归,需要递归调用栈的支持,而栈的长度取决于递归调用的深度(即使不用递归,也需要用用户栈)。在平均情况下,需要O(logn)的栈空间;最坏情况下,栈空间可达O(n)。
快速排序同前面的希尔排序,它也是不稳定的排序算法。例如:49,38,49*,20,97,76,经过一次划分后:20,38,49*,49,97,76。
快速排序不适于对原本有序或基本有序的记录序列进行排序。例如,对(46,50,68,74,79,85,90)进行快速排序,会发现:由于每次枢轴记录的关键字都是小于其它所有记录的关键字,致使一次划分之后得到的子序列(1)的长度为0,这时已经退化成为没有改进措施的冒泡排序。
划分元素的选取是影响时间性能的关键。输入数据次序越乱,所选划分元素值的随机性越好,排序速度反而越快,快速排序不是自然排序方法。需要注意的是,改变划分元素的选取方法,至多只能改变算法平均情况的下的世界性能,无法改变最坏情况下的时间性能。即最坏情况下,快速排序的时间复杂度总是O(n^2)。
相关文章:

24.排序,插入排序,交换排序
目录 一. 插入排序 (1)直接插入排序 (2)折半插入排序 (3)希尔排序 二. 交换排序 (1)冒泡排序 (2)快速排序 排序:将一组杂乱无章的数据按一…...
Navicat16安装教程
注:因版权原因,本文已去除破解相关的文件和内容 1、在本站下载解压后即可获得Navicat16安装包和破解补丁,如图所示 2、双击“navicat160_premium_cs_x64.exe”程序,即可进入安装界面, 3、点击下一步 4、如图所示勾选“…...

【看表情包学Linux】初识文件描述符 | 虚拟文件系统 (VFS) 初探 | 系统传递标记位 | O_TRUNC | O_APPEND
爆笑教程《看表情包学Linux》👈 猛戳订阅! 💭 写在前面:通过上一章节的讲解,想必大家已对文件系统基本的接口有一个简单的了解,本章我们将继续深入讲解,继续学习系统传递标志位&…...
ssm+vue“魅力”繁峙宣传网站源码和论文
ssmvue“魅力”繁峙宣传网站源码和论文102 开发工具:idea 数据库mysql5.7 数据库链接工具:navcat,小海豚等 技术:ssm 摘 要 随着科学技术的飞速发展,各行各业都在努力与现代先进技术接轨,通过科技手段提高自身…...
Linux系统编程5(线程概念详解)
线程同进程一样都是OS中非常重要的部分,线程的应用场景非常的广泛,试想我们使用的视频软件,在网络不是很好的情况下,通常会采取下载的方式,现在你很想立即观看,又想下载,于是你点击了下载并且在…...

leetcode645. 错误的集合(java)
错误的集合 题目描述优化空间代码演示 题目描述 难度 - 简单 LC645 - 错误的集合 集合 s 包含从 1 到 n 的整数。不幸的是,因为数据错误,导致集合里面某一个数字复制了成了集合里面的另外一个数字的值,导致集合 丢失了一个数字 并且 有一个数…...

Pytest参数详解 — 基于命令行模式
1、--collect-only 查看在给定的配置下哪些测试用例会被执行 2、-k 使用表达式来指定希望运行的测试用例。如果测试名是唯一的或者多个测试名的前缀或者后缀相同,可以使用表达式来快速定位,例如: 命令行-k参数.png 3、-m 标记࿰…...

【python爬虫】3.爬虫初体验(BeautifulSoup解析)
文章目录 前言BeautifulSoup是什么BeautifulSoup怎么用解析数据提取数据 对象的变化过程总结 前言 上一关,我们学习了HTML基础知识,知道了HTML是一种用来描述网页的语言,又了解了HTML的基本结构。 认识了HTML中的常见标签和常见属性&#x…...
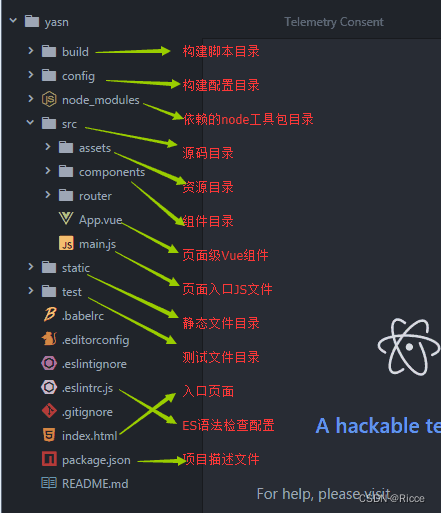
【Three.js + Vue 构建三维地球-Part One】
Three.js Vue 构建三维地球-Part One Vue 初始化部分Vue-cli 安装初始化 Vue 项目调整目录结构 Three.js 简介Three.js 安装与开始使用 实习的第一个任务是完成一个三维地球的首屏搭建,看了很多的案例,也尝试了用 Echarts 3D地球的模型进行构建…...
Power View
界面 切换可视化效果 对于已经上传到透视表的数据,选择power view,形成表格后。...

SQL查询本年每月的数据
--一、以一行数据的形式,显示本年的12月的数据,本示例以2017年为例,根据统计日期字段判断,计算总和,查询语句如下:selectsum(case when datepart(month,统计日期)1 then 支付金额 else 0 end) as 1月, sum…...

C++之struct和union对比介绍
C之struct和union对比介绍 在C中,struct和union都是用来定义自定义数据类型的关键字,但它们的作用略有不同。 首先了解一下它们的基本概念: struct(结构体):struct 是一个用户自定义的数据类型ÿ…...

微服务--SkayWalking(链路追踪:国产开源框架)
SkayWalking:分布式系统的应用程序性能监视工具 作用:分布式追踪、性能指标分析、应用、服务依赖分析; SkayWalking性能剖析: 我操,能够定位到某一个方法会有多慢。。。 通过Tid查看全局所有的日志信息(…...

在Windows 10上部署ChatGLM2-6B:掌握信息时代的智能对话
在Windows 10上部署ChatGLM2-6B:掌握信息时代的智能对话 硬件环境ChatGLM2-6B的量化模型最低GPU配置说明准备工作ChatGLM2-6B安装部署ChatGLM2-6B运行模式解决问题总结 随着当代科技的快速发展,我们进入了一个数字化时代,其中信息以前所未有的…...

LRU和LFU算法的简单实现
LRU #include <iostream> #include <unordered_map> #include <list> struct Node{int key;int value;Node(int key, int value):key(key),value(value){} }; class LruCache{ private:int maxCapacity;// 最大容量std::list<Node>CacheList;// 缓存链…...

OCR多语言识别模型构建资料收集
OCR多语言识别模型构建 构建多语言识别模型方案 合合,百度,腾讯,阿里这四家的不错 调研多家,发现有两种方案,但是大多数厂商都是将多语言放在一个字典里,构建1w~2W的字典,训练一个可识别多种语…...

倍增的经典题目:扩大区间、st表
1. 扩大区间 P4155 [SCOI2015] 国旗计划例题1:P4155 [SCOI2015] 国旗计划 计算能覆盖整个圆圈的最少区间,题目给定的所有区间互相不包含,按区间左端点排序后,区间的右端点也是单增的。 我们首先需要化圆为线,然后贪…...
)
LeetCode——和为K的子数组(中等)
题目 给你一个整数数组 nums 和一个整数 k ,请你统计并返回 该数组中和为 k 的连续子数组的个数 。 示例 1: 输入:nums [1,1,1], k 2 输出:2示例 2: 输入:nums [1,2,3], k 3 输出:2 题解 …...

Truncation Sampling as Language Model Desmoothing
本文是LLM系列文章,针对《Truncation Sampling as Language Model Desmoothing》的翻译。 截断采样作为语言模型的去平滑性 摘要1 引言2 背景3 截断作为去平滑性4 方法5 实验与结果6 相关工作7 结论8 不足 摘要 来自神经语言模型的长文本样本可能质量较差。截断采…...
docker安装jenkins
运行jenkins docker run -d \--name jenkins \ --hostname jenkins \-u root \-p 29090:8080 \--restart always \-v D:\springcloud\学习\jekins\jenkins\jks_home:/var/jenkins_home \ jenkins/jenkins获取root登录密码 密码在jekins_home/secrets/initalAdminPassword文件…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

【WebSocket】SpringBoot项目中使用WebSocket
1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖,添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...

实战设计模式之模板方法模式
概述 模板方法模式定义了一个操作中的算法骨架,并将某些步骤延迟到子类中实现。模板方法使得子类可以在不改变算法结构的前提下,重新定义算法中的某些步骤。简单来说,就是在一个方法中定义了要执行的步骤顺序或算法框架,但允许子类…...

GB/T 43887-2024 核级柔性石墨板材检测
核级柔性石墨板材是指以可膨胀石墨为原料、未经改性和增强、用于核工业的核级柔性石墨板材。 GB/T 43887-2024核级柔性石墨板材检测检测指标: 测试项目 测试标准 外观 GB/T 43887 尺寸偏差 GB/T 43887 化学成分 GB/T 43887 密度偏差 GB/T 43887 拉伸强度…...
