倍增的经典题目:扩大区间、st表
1. 扩大区间
P4155 [SCOI2015] 国旗计划例题1:P4155 [SCOI2015] 国旗计划
计算能覆盖整个圆圈的最少区间,题目给定的所有区间互相不包含,按区间左端点排序后,区间的右端点也是单增的。
我们首先需要化圆为线,然后贪心(优化为倍增)选择一个右端点最远的线段,并且该线段的左端点在上个线段的内部。
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 4e5+10;
struct seg{int id, l, r;bool operator < (const seg & x) const{return l < x.l;}
}a[N];
int go[N][20]; //倍增
int n, m, ans[N];
void init() {int nxt = 1;for(int i = 1; i<=n*2; i++) {while(nxt <= n*2 && a[nxt].l <= a[i].r) nxt++;go[i][0] = nxt - 1;}for(int i = 1; (1<<i) <= n; i++) { //最多跳2^n, 不超过n for(int st = 1; st <= n*2; st++) {go[st][i] = go[go[st][i-1]][i-1];}}
}
void getans(int x){int now = x, res = 1; //从第x个战士出发 for(int i = log2(N); i>=0; i--){ //注意二进制是从高位开始枚举 int pos = go[now][i];if(pos && a[pos].r < a[x].l + m) { //跳的那个位置不超过一圈后的自己 res += 1<<i;now = pos; //就可以跳 }}ans[a[x].id] = res+1;
}
int main() {scanf("%d%d", &n, &m);for(int i = 1; i<=n; i++) {scanf("%d%d", &a[i].l, &a[i].r);a[i].id = i;if(a[i].r < a[i].l) a[i].r += m; //化圆为链 }sort(a+1, a+n+1);for(int i = 1; i<=n; i++){ //每一个线段的终点是自己, 想想a[n]是要绕一圈到a[1]的 a[i+n].id = a[i].id;a[i+n].l = a[i].l + m;a[i+n].r = a[i].r + m;}init();for(int i = 1; i<=n; i++) getans(i);for(int i = 1; i<=n; i++){printf("%d ", ans[i]);}return 0;
}例题2:2021年中国大学生程序设计竞赛女生专场 B攻防演练
与上面的代码很像,大概原理都一样的
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5+10;
int pos[30], n, m, dp[N][30];
int main(){scanf("%d%d", &m, &n);string s; cin>>s;s = '#' + s;for(int i = 0; i<=20; i++) dp[n+1][i] = n+1; //需要初始化边界, 因为有的dp会跳到最后 for(int i = 0; i<26; i++) pos[i] = n+1;for(int i = n; i >= 0; i--){ //i = 0也要更新, 因为从l-1开始跳 for(int j = 0; j<m; j++)dp[i][0] = max(dp[i][0], pos[j]);if(i) pos[s[i]-'a'] = i;}for(int j = 1; j <= 20; j ++){ //枚举区间长度 for(int i = 0; i <= n; i++){dp[i][j] = dp[dp[i][j-1]][j-1];//以i开始跳, 跳2^j次后到达的最大位置; 即以i开始跳, 先跳2^(j-1)次, 然后再跳2^(j-1)次 }}int q; scanf("%d", &q);while(q--) {int l, r; scanf("%d%d", &l, &r);int ans = 1, p = l-1;for(int j = 20; j>=0; j--){if(dp[p][j]<=r) {p = dp[p][j];ans += (1<<j);}}printf("%d\n", ans);} return 0;
}2. 区间最大/最小值,st表
如果元素满足倍增关系,例如快速幂、LCA都可以用到倍增
区间最大值:
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5+10, M = 25;
int dp[N][M];
int main() {int n; scanf("%d", &n);for(int i = 1; i <= n; i++) scanf("%d", &dp[i][0]);for(int j = 1; j <= 20; j++){ //首先枚举区间长度 for(int i = 1; i+(1<<j)-1 <= n; i++){ //再枚举起点 dp[i][j] = max(dp[i][j-1], dp[i+(1<<(j-1))][j-1]);}}int q; scanf("%d", &q);while(q--) {int l, r; scanf("%d%d", &l, &r);int k = log2(r-l+1); //区间长度的指数 printf("%d\n", max(dp[l][k], dp[r-(1<<k)+1][k]));}return 0;
}相关文章:

倍增的经典题目:扩大区间、st表
1. 扩大区间 P4155 [SCOI2015] 国旗计划例题1:P4155 [SCOI2015] 国旗计划 计算能覆盖整个圆圈的最少区间,题目给定的所有区间互相不包含,按区间左端点排序后,区间的右端点也是单增的。 我们首先需要化圆为线,然后贪…...
)
LeetCode——和为K的子数组(中等)
题目 给你一个整数数组 nums 和一个整数 k ,请你统计并返回 该数组中和为 k 的连续子数组的个数 。 示例 1: 输入:nums [1,1,1], k 2 输出:2示例 2: 输入:nums [1,2,3], k 3 输出:2 题解 …...

Truncation Sampling as Language Model Desmoothing
本文是LLM系列文章,针对《Truncation Sampling as Language Model Desmoothing》的翻译。 截断采样作为语言模型的去平滑性 摘要1 引言2 背景3 截断作为去平滑性4 方法5 实验与结果6 相关工作7 结论8 不足 摘要 来自神经语言模型的长文本样本可能质量较差。截断采…...
docker安装jenkins
运行jenkins docker run -d \--name jenkins \ --hostname jenkins \-u root \-p 29090:8080 \--restart always \-v D:\springcloud\学习\jekins\jenkins\jks_home:/var/jenkins_home \ jenkins/jenkins获取root登录密码 密码在jekins_home/secrets/initalAdminPassword文件…...
学习pytorch8 土堆说卷积操作
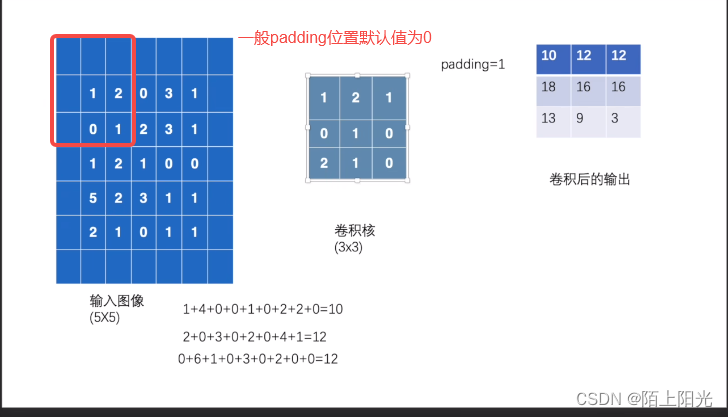
土堆说卷积操作 官网debug torch版本只有nn 没有nn.functional代码执行结果 B站小土堆视频学习笔记 官网 https://pytorch.org/docs/stable/nn.html#convolution-layers 常用torch.nn, nn是对nn.functional的封装,使函数更易用。 卷积核从输入图像左上角…...
pytest自动化测试两种执行环境切换的解决方案
目录 一、痛点分析 方法一:Hook方法pytest_addoption注册命令行参数 1、Hook方法注解 2、使用方法 方法二:使用插件pytest-base-url进行命令行传参 一、痛点分析 在实际企业的项目中,自动化测试的代码往往需要在不同的环境中进行切换&am…...

说说TIME_WAIT和CLOSE_WAIT区别
分析&回答 TCP协议规定,对于已经建立的连接,网络双方要进行四次握手才能成功断开连接,如果缺少了其中某个步骤,将会使连接处于假死状态,连接本身占用的资源不会被释放。网络服务器程序要同时管理大量连接…...

Docker的优势
Docker是一种开源的容器化平台,提供了一种将应用程序、库和其它依赖项封装在容器中的方法。以下是Docker的基本概念和优势: 基本概念: 镜像:一个Docker镜像是一个可运行的软件包,包括应用程序、库和其它依赖项。它是D…...

C++——string使用
string的常见构造接口 string() 构造空的srting类对象,空字符串 string(const char* str) 用字符串初始化 string(const string& str)拷贝构造,使用string类初始化string(size_t n, char c) 用n个字符c初始化 string s1; string s2("hello …...
10. selenium API (二)
目录 1. 多层框架/窗口定位 2. 下拉框处理 2.1 前端界面 2.2 代码 3. 针对 alert 弹窗进行操作 3.1 前端界面 3.2 代码 4. 文件提交 4.1 前端界面 4.2 代码 5. 显示等待 6. 操作浏览器滚动条 7. 截图 8. 浏览器关闭 9. 窗口切换 在上篇文章中,我们学…...

[国产MCU]-W801开发实例-用户报文协议(UDP)数据接收和发送
用户报文协议(UDP)数据接收和发送 文章目录 用户报文协议(UDP)数据接收和发送1、UDP简单介绍2、W801的UDP创建逻辑2.1 UDP使用步骤2.2 代码实现1、UDP简单介绍 用户数据报协议 (UDP) 是一种跨互联网使用的通信协议,用于对时间敏感的传输,例如视频播放或 DNS查找。它通过在数…...
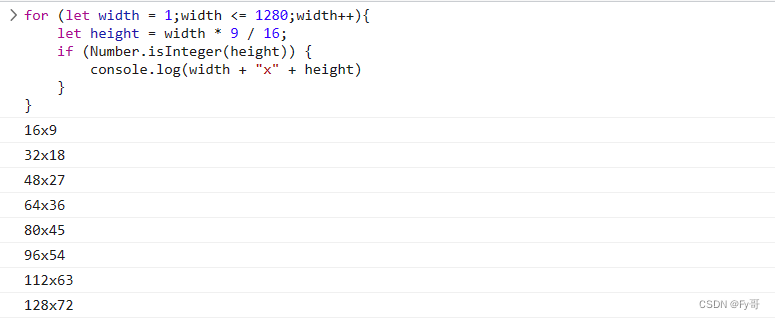
JavaScript 生成 16: 9 宽高比
这篇文章只是对 for 循环一个简单应用,没有什么知识含量。 可以跳过这篇文章。 只是我用来保存一下我的代码,保存在本地我嫌碍眼,总想把他删了。 正文部分 公式:其中 width 表示宽度,height 表示高度 16 9 w i d t…...
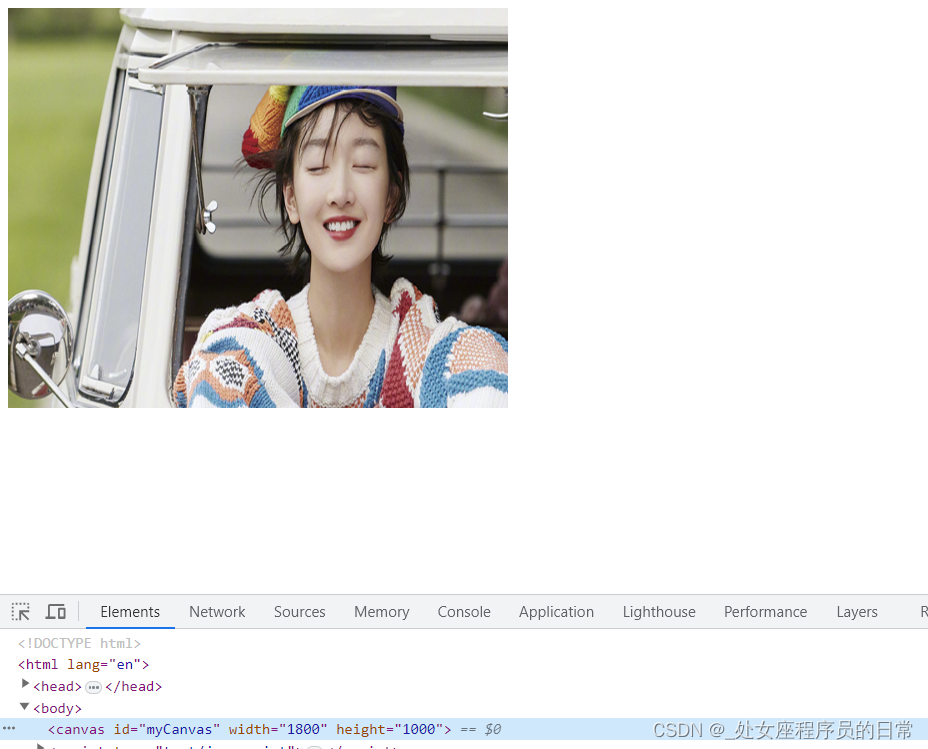
HTML5之drawImage函数
参数说明: drawImage(image, x, y) //按原图片大小绘制。 drawImage(image, x, y, width, height) //按指定大小绘制。 drawImage(image, sourceX, sourceY, sourceWidth, sourceHeight, destX, destY, destWidth, destHeight) //常用于图片裁剪。 其中:…...

leetcode7.整数反转-Java
题目 给你一个 32 位的有符号整数 x ,返回将 x 中的数字部分反转后的结果。 如果反转后整数超过 32 位的有符号整数的范围 [−231, 231 − 1] ,就返回 0。 假设环境不允许存储 64 位整数(有符号或无符号)。 7. 整数反转 - 力扣&a…...

操作系统备考学习 day2 (1.3.2 - 1.6)
操作系统备考学习 day2 计算机系统概述操作系统运行环境中断和异常的概念系统调用 操作系统体系结构操作系统引导虚拟机 计算机系统概述 操作系统运行环境 中断和异常的概念 中断的作用 CPU上会运行两种程序,一种是操作系统内核程序,一种是应用程序。…...

Django-跨域
一、基础概念 cors 跨域资源共享 二、跨域请求-简单请求 满足以下全部条件的请求为 简单请求 1.请求方法如下: GET or HEAR or POS 2.请求头仅包含如下: Accept、Accept-Language、Content-Language、Content-Type 3.ConTent-Type 仅支持如下三种&…...
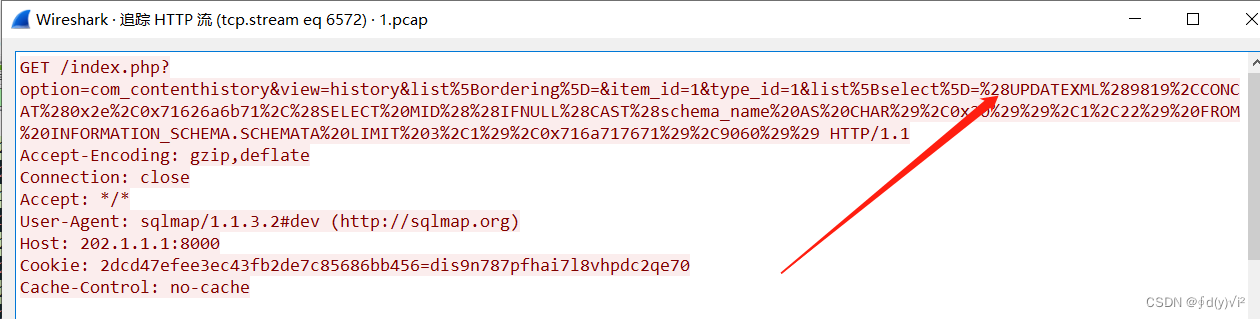
wireshark抓包体验
目录 1、使用基础 1.1 数据包筛选 1.2 MAC地址筛选 1.3 端口筛选 1.4 协议筛选 1.5 包长度筛选 1.6 http请求筛选 2.数据包搜索 3.数据包还原 2、例题复现 1、使用基础 1.1 数据包筛选 ip.src 源ip地址 同理可以得到筛选目标地址: ip.dst 目的ip地址 1.2 …...
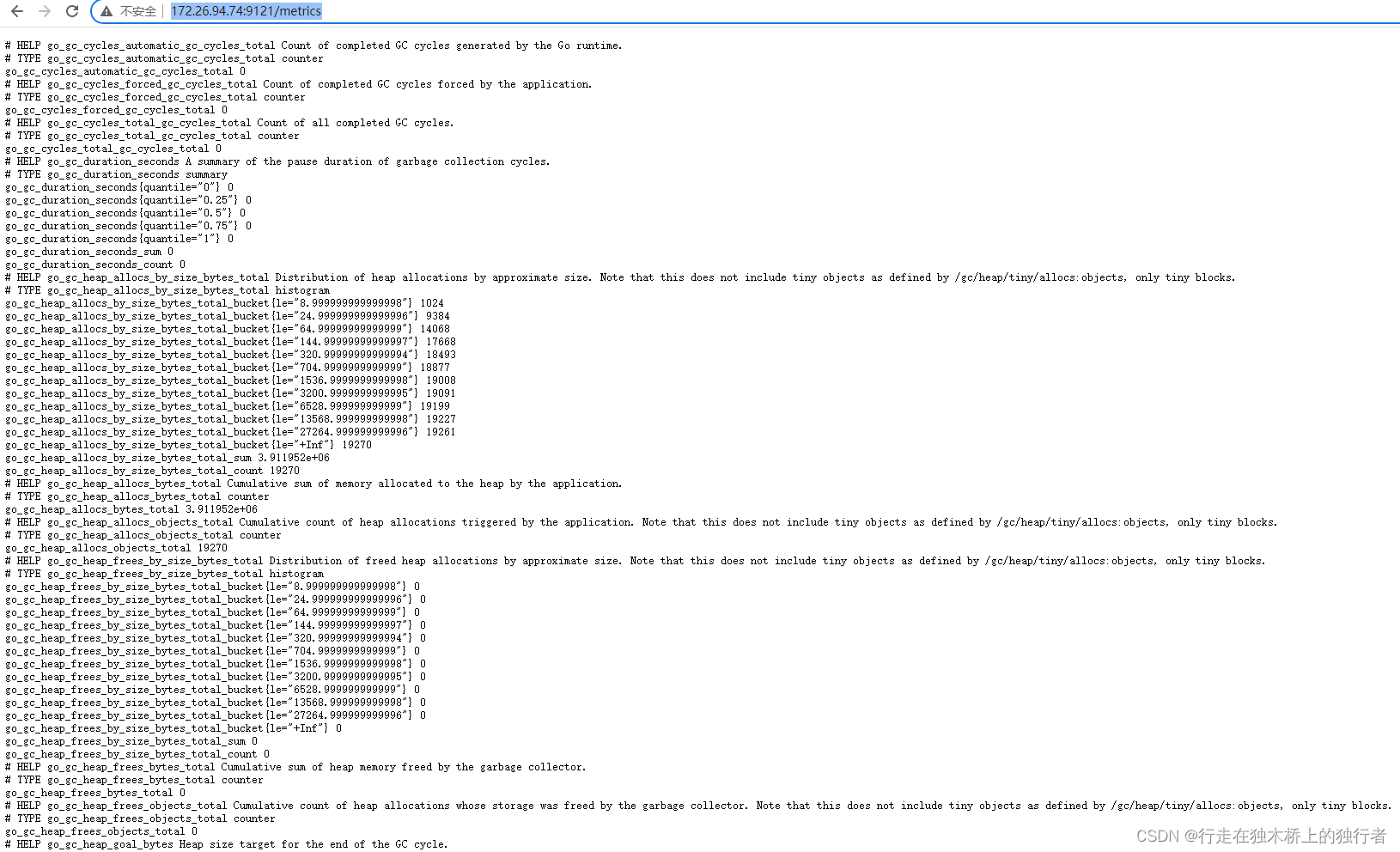
Prometheus+grafana安装配置
Prometheus安装配置 Prometheus下载地址 官方地址:Download | Prometheus 可根据系统版本下载想要的安装包,复制链接地址 wget https://github.com/prometheus/prometheus/releases/download/v2.33.3/prometheus-2.33.3.linux-amd64.tar.gzwg 解压pr…...

长连接和短连接有什么区别?
长连接和短连接是什么? HTTP的长连接和短连接本质上是TCP长连接和短连接。HTTP属于应用层协议,在传输层使用TCP协议,在网络层使用IP协议。 IP协议主要解决网络路由和寻址问题,TCP协议主要解决如何在IP层之上可靠地传递数据包&…...
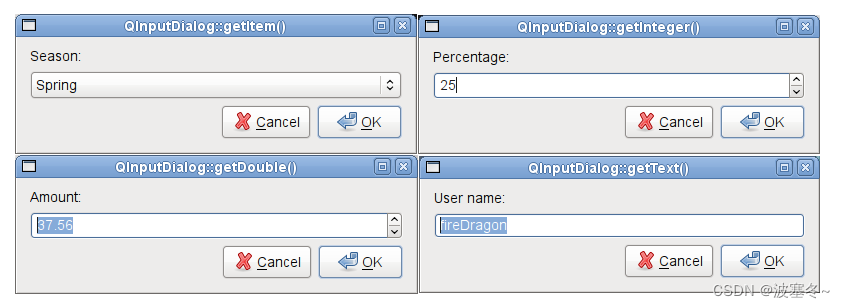
Qt应用开发(基础篇)——输入对话框 QInputDialog
一、前言 QInputDialog类继承于QDialog,是一个简单方便的对话框,用于从用户获取单个值。 对话框窗口 QDialog QInputDialog输入对话框带有一个文本标签、一个输入框和标准按钮。输入内容可以字符、数字和选项,文本标签用来告诉用户应该要输入…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...

Visual Studio Code 扩展
Visual Studio Code 扩展 change-case 大小写转换EmmyLua for VSCode 调试插件Bookmarks 书签 change-case 大小写转换 https://marketplace.visualstudio.com/items?itemNamewmaurer.change-case 选中单词后,命令 changeCase.commands 可预览转换效果 EmmyLua…...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...
