机器学习笔记之最优化理论与方法(五)凸优化问题(上)
机器学习笔记之最优化理论与方法——凸优化问题[上]
- 引言
- 凸优化问题的基本定义
- 凸优化定义:示例
- 凸优化与非凸优化问题的区分
- 局部最优解即全局最优解
- 凸优化问题的最优性条件
- 几种特殊凸问题的最优性条件
- 无约束凸优化
- 等式约束凸优化
- 非负约束凸优化
引言
本节将介绍凸优化问题,主要介绍凸优化问题的基本定义、凸优化与非凸优化问题的区分。
凸优化问题的基本定义
关于最优化问题 P \mathcal P P描述如下:
P ⇒ { min f ( x 1 , x 2 , ⋯ , x n ) s.t. { G i ( x 1 , x 2 , ⋯ , x n ) ≤ 0 i = 1 , 2 , ⋯ , m H j ( x 1 , x 2 , ⋯ , x n ) = 0 j = 1 , 2 , ⋯ , l \mathcal P \Rightarrow \begin{cases} \min f(x_1,x_2,\cdots,x_n) \\ \text{s.t. } \begin{cases} \mathcal G_i(x_1,x_2,\cdots,x_n) \leq 0 \quad i=1,2,\cdots,m \\ \mathcal H_j(x_1,x_2,\cdots,x_n) = 0 \quad j=1,2,\cdots,l \end{cases} \end{cases} P⇒⎩ ⎨ ⎧minf(x1,x2,⋯,xn)s.t. {Gi(x1,x2,⋯,xn)≤0i=1,2,⋯,mHj(x1,x2,⋯,xn)=0j=1,2,⋯,l
同时记最优化问题的可行域 S \mathcal S S为:
从可行域中采样出的 x ∈ S x \in \mathcal S x∈S也被称作可行解。
S = { x ∈ R n ∣ G i ( x ) ≤ 0 , i = 1 , 2 , ⋯ , m ; H j ( x ) = 0 , j = 1 , 2 , ⋯ , l } \mathcal S = \{x \in \mathbb R^n \mid \mathcal G_i(x) \leq 0,i=1,2,\cdots,m;\mathcal H_j(x) = 0,j=1,2,\cdots,l\} S={x∈Rn∣Gi(x)≤0,i=1,2,⋯,m;Hj(x)=0,j=1,2,⋯,l}
什么情况下,最优化问题 P \mathcal P P被称作凸优化问题 ? ? ?针对上述描述,需要满足如下三个条件:
- 目标函数 f ( x ) f(x) f(x)是关于决策变量 x x x的凸函数;
- m m m个不等式约束函数 G i ( x ) , i = 1 , 2 , ⋯ , m \mathcal G_i(x),i=1,2,\cdots,m Gi(x),i=1,2,⋯,m均是关于决策变量 x x x的凸函数;
- l l l个等式约束函数 H j ( x ) , j = 1 , 2 , ⋯ , l \mathcal H_j(x),j=1,2,\cdots,l Hj(x),j=1,2,⋯,l均是关于决策变量 x x x的线性函数。
观察不等式约束函数 G i ( x ) \mathcal G_i(x) Gi(x),为什么要强调它们是凸函数 ? ? ?,首先,观察不等式约束的描述:
G i ( x ) ≤ 0 i = 1 , 2 , ⋯ , m \mathcal G_i(x) \leq 0 \quad i=1,2,\cdots,m Gi(x)≤0i=1,2,⋯,m
这种描述明显是:关于函数 G i ( x ) \mathcal G_i(x) Gi(x)在水平值 a = 0 a=0 a=0处的水平集 L i ; 0 \mathcal L_{i;0} Li;0:
关于水平集的概念,详见凸函数:定义与基本性质。
L i ; 0 = { x ∣ G i ( x ) ≤ 0 , x ∈ R n ; i = 1 , 2 , ⋯ , m } \mathcal L_{i;0} = \{x \mid \mathcal G_i(x) \leq 0,x \in \mathbb R^n;i=1,2,\cdots,m\} Li;0={x∣Gi(x)≤0,x∈Rn;i=1,2,⋯,m}
根据水平集的定义:如果 G i ( x ) , i = 1 , 2 , ⋯ , m \mathcal G_i(x),i=1,2,\cdots,m Gi(x),i=1,2,⋯,m是凸函数,那么其对应的水平集 L i ; 0 , i = 1 , 2 , ⋯ , m \mathcal L_{i;0},i=1,2,\cdots,m Li;0,i=1,2,⋯,m必然是凸集。而 m m m个不等式约束对应的结果是 m m m个水平集的交集,而该交集必然也是凸集。
关于凸集的交集也是凸集同样见上述链接几种保持函数凸性的运算。
同样,观察等式约束函数 H j ( x ) , j = 1 , 2 , ⋯ , l \mathcal H_j(x),j=1,2,\cdots,l Hj(x),j=1,2,⋯,l,如果它们是线性函数:
H j ( x ) : A j T x + b j = 0 j = 1 , 2 , ⋯ , l \mathcal H_j(x):\mathcal A_j^T x + b_j = 0 \quad j=1,2,\cdots,l Hj(x):AjTx+bj=0j=1,2,⋯,l
而线性函数同样是凸函数,因而等式约束函数描述的集合同样也是凸集。从而在上述两类约束条件下的可行域 S \mathcal S S也必然是凸集。根据凸集的简单认识中介绍的:凸优化问题与凸集合凸函数的关系中的两个条件:
- 目标函数 f ( x ) f(x) f(x)是一个凸函数;
- x x x的可行域 S ⇒ x ∈ S \mathcal S \Rightarrow x \in \mathcal S S⇒x∈S是一个凸集;
满足条件的最优化问题才属于凸优化问题。
相反,如果目标函数 f ˉ ( x ) \bar{f}(x) fˉ(x)描述为: max f ˉ ( x ) \max \bar{f}(x) maxfˉ(x),想要将其转化为凸优化问题,我们需要判定: f ˉ ( x ) \bar{f}(x) fˉ(x)是否为凹函数。如果 f ˉ ( x ) \bar{f}(x) fˉ(x)是凹函数,可以将其转化为相应凸函数的优化问题:
关于凹函数,同样见凸函数:定义与基本性质。
max f ˉ ( x ) ⇔ min − f ˉ ( x ) \max \bar{f}(x) \Leftrightarrow \min - \bar{f}(x) maxfˉ(x)⇔min−fˉ(x)
凸优化定义:示例
观察:下面的最优化问题是否为凸优化问题 ? ? ?
{ min f ( x ) = x 1 2 + x 2 2 s.t. { G ( x ) = x 1 1 + x 2 2 ≤ 0 H ( x ) = ( x 1 + x 2 ) 2 = 0 \begin{cases} \min f(x) = x_1^2 + x_2^2 \\ \text{s.t. } \begin{cases} \begin{aligned} \mathcal G(x) & = \frac{x_1}{1 + x_2^2} \leq 0 \\ \mathcal H(x) & = (x_1 + x_2)^2 = 0 \end{aligned} \end{cases} \end{cases} ⎩ ⎨ ⎧minf(x)=x12+x22s.t. ⎩ ⎨ ⎧G(x)H(x)=1+x22x1≤0=(x1+x2)2=0
- 首先,观察到该最优化问题是最小化问题,并且目标函数 f ( x ) = x 1 2 + x 2 2 f(x) = x_1^2 + x_2^2 f(x)=x12+x22是凸函数;
该函数对应决策变量 x x x的 Hessian Matrix ⇒ ∇ 2 f ( x ) \text{Hessian Matrix} \Rightarrow \nabla^2 f(x) Hessian Matrix⇒∇2f(x)是固定结果:( 2 0 0 2 ) \begin{pmatrix}2 \quad 0 \\ 0 \quad 2\end{pmatrix} (2002),它是一个正定矩阵(凸函数的二阶条件)。 - 观察不等式约束 G ( x ) = x 1 1 + x 2 2 \begin{aligned}\mathcal G(x) = \frac{x_1}{1 + x_2^2}\end{aligned} G(x)=1+x22x1,从表面上看:它并不是一个凸函数。但我们可以推出如下表达:
由于分母1 + x 2 2 > 0 1 +x_2^2 > 0 1+x22>0恒成立,因此只需要观察分子的符号即可。
G ( x ) = x 1 1 + x 2 2 ≤ 0 ⇔ x 1 ≤ 0 ⇒ G ˉ ( x ) = x 1 \mathcal G(x) = \frac{x_1}{1 + x_2^2} \leq 0 \Leftrightarrow x_1 \leq 0 \Rightarrow \bar{\mathcal G}(x) = x_1 G(x)=1+x22x1≤0⇔x1≤0⇒Gˉ(x)=x1
而 G ˉ ( x ) = x 1 \bar{\mathcal G}(x) = x_1 Gˉ(x)=x1是线性函数,自然也是凸函数; - 观察等式约束 H ( x ) = ( x 1 + x 2 ) 2 = 0 \mathcal H(x) = (x_1 + x_2)^2 = 0 H(x)=(x1+x2)2=0,很明显它不是线性函数。但我们同样可以推出如下表达:
H = ( x 1 + x 2 ) 2 = 0 ⇔ x 1 + x 2 = 0 ⇒ H ˉ ( x ) = x 1 + x 2 \mathcal H = (x_1 + x_2)^2 =0 \Leftrightarrow x_1 + x_2 = 0 \Rightarrow \bar{\mathcal H}(x) = x_1 + x_2 H=(x1+x2)2=0⇔x1+x2=0⇒Hˉ(x)=x1+x2
而 H ˉ ( x ) \bar{\mathcal H}(x) Hˉ(x)是线性函数。综上,该示例描述的最优化问题是凸优化问题。
关于约束条件,可能并不是上来直接用,能够化简的部分需要进行化简。
凸优化与非凸优化问题的区分
在凸集的简单认识中,介绍了凸优化相关的两个优秀性质:
局部最优解即全局最优解
关于局部最优解 x ˉ \bar{x} xˉ的定义表示为:
f ( x ˉ ) ≤ f ( x ) ∀ ∈ S ∩ N ϵ ( x ˉ ) f(\bar{x}) \leq f(x) \quad \forall \in \mathcal S \cap \mathcal N_{\epsilon}(\bar {x}) f(xˉ)≤f(x)∀∈S∩Nϵ(xˉ)
其中 N ϵ ( x ˉ ) \mathcal N_{\epsilon}(\bar{x}) Nϵ(xˉ)表示包含 x ˉ \bar{x} xˉ的小的邻域范围。也就是说:仅在较小的邻域范围 S ∩ N ϵ ( x ˉ ) \mathcal S \cap \mathcal N_{\epsilon}(\bar{x}) S∩Nϵ(xˉ)内,某可行解 x ˉ \bar{x} xˉ的目标函数值 ≤ \leq ≤所有目标函数值,称可行解 x ˉ \bar{x} xˉ为局部最优解;
相反,关于全局最优解 x ∗ x^* x∗的定义表示为:
f ( x ∗ ) ≤ f ( x ) ∀ x ∈ S f(x^*) \leq f(x) \quad \forall x \in \mathcal S f(x∗)≤f(x)∀x∈S
也就是说:在整个可行域 S \mathcal S S范围内,某可行解 x ∗ x^* x∗的目标函数值 ≤ \leq ≤所有目标函数值。称可行解 x ∗ x^* x∗为全局最优解。
回到凸优化问题上:如果在 S \mathcal S S中找到某一个局部最优解,那么该解一定也是全局最优解。
(反证法)证明:
- 假设找到某个解 x ˉ \bar{x} xˉ是局部最优解,但不是全局最优解,可以推出:必然存在某个解 x ∗ ∈ S x^* \in \mathcal S x∗∈S,有:
如果不存在,这个局部解就是全局解~
f ( x ∗ ) < f ( x ˉ ) f(x^*) < f(\bar{x}) f(x∗)<f(xˉ) - 从 x ˉ \bar{x} xˉ开始,沿着 x ∗ − x ˉ x^* - \bar{x} x∗−xˉ方向前进一个小的步长,得到一个新的点: x ˉ + λ ⋅ ( x ∗ − x ˉ ) , λ ∈ ( 0 , 1 ) \bar {x} + \lambda \cdot (x^* - \bar{x}),\lambda \in (0,1) xˉ+λ⋅(x∗−xˉ),λ∈(0,1),它的目标函数结果: f [ x ˉ + λ ⋅ ( x ∗ − x ˉ ) ] f[\bar{x} + \lambda \cdot (x^* - \bar{x})] f[xˉ+λ⋅(x∗−xˉ)]可表示为:
可以将x ˉ + λ ⋅ ( x ∗ − x ˉ ) = ( 1 − λ ) ⋅ x ˉ + λ ⋅ x ∗ \bar{x} + \lambda \cdot (x^* - \bar{x}) = (1 - \lambda) \cdot \bar{x} + \lambda \cdot x^* xˉ+λ⋅(x∗−xˉ)=(1−λ)⋅xˉ+λ⋅x∗重新组合,可看作点x ˉ , x ∗ \bar{x},x^* xˉ,x∗的凸组合。
将上面的f ( x ∗ ) < f ( x ˉ ) f(x^*) <f(\bar{x}) f(x∗)<f(xˉ)代入。
f [ λ ⋅ x ∗ + ( 1 − λ ) ⋅ x ˉ ] ≤ λ ⋅ f ( x ∗ ) + ( 1 − λ ) ⋅ f ( x ˉ ) < λ ⋅ f ( x ˉ ) + ( 1 − λ ) ⋅ f ( x ˉ ) = f ( x ˉ ) \begin{aligned} f[\lambda \cdot x^* + (1 - \lambda) \cdot \bar{x}] & \leq \lambda \cdot f(x^*) + (1 - \lambda) \cdot f(\bar{x}) \\ & < \lambda \cdot f(\bar{x}) + (1 - \lambda) \cdot f(\bar{x}) \\ & = f(\bar{x}) \end{aligned} f[λ⋅x∗+(1−λ)⋅xˉ]≤λ⋅f(x∗)+(1−λ)⋅f(xˉ)<λ⋅f(xˉ)+(1−λ)⋅f(xˉ)=f(xˉ) - 可以发现:无论 λ \lambda λ如何取值, f [ x ˉ + λ ⋅ ( x ∗ − x ˉ ) ] < f ( x ˉ ) f[\bar{x} + \lambda \cdot (x^* - \bar{x})] < f(\bar{x}) f[xˉ+λ⋅(x∗−xˉ)]<f(xˉ)恒成立。如果 λ ⇒ 0 \lambda \Rightarrow 0 λ⇒0,小到 x ˉ + λ ⋅ ( x ∗ − x ˉ ) \bar{x} + \lambda \cdot (x^* - \bar{x}) xˉ+λ⋅(x∗−xˉ)位于局部最优解邻域 N ϵ ( x ˉ ) \mathcal N_{\epsilon}(\bar{x}) Nϵ(xˉ)内,会出现矛盾: x ˉ \bar{x} xˉ是该邻域内的最优解,但存在另一个解 x ˉ + λ ⋅ ( x ∗ − x ˉ ) \bar{x} +\lambda \cdot (x^* - \bar{x}) xˉ+λ⋅(x∗−xˉ),其函数值小于 f ( x ˉ ) f(\bar{x}) f(xˉ),这意味着: x ˉ \bar{x} xˉ不是该邻域内的最优解。至此,得证:如过 x ˉ \bar{x} xˉ是局部最优解,那么它一定是全局最优解。
凸优化问题的最优性条件
什么样的解是凸优化问题的最优解 ? ? ?关于最优解有如下充要条件:
x ∗ ∈ S is Optimal ⇔ [ ∇ f ( x ∗ ) ] T ( x − x ∗ ) ≥ 0 ∀ x ∈ S x^* \in \mathcal S \text{ is Optimal } \Leftrightarrow [\nabla f(x^*)]^T (x - x^*) \geq 0 \quad \forall x \in \mathcal S x∗∈S is Optimal ⇔[∇f(x∗)]T(x−x∗)≥0∀x∈S
为什么满足该充要条件就一定是最优解 ? ? ?证明如下:
充分性:已知某解 x ∗ x^* x∗满足 [ ∇ f ( x ∗ ) ] T ( x − x ∗ ) ≥ 0 , ∀ x ∈ S [\nabla f(x^*)]^T(x - x^*) \geq 0,\forall x \in \mathcal S [∇f(x∗)]T(x−x∗)≥0,∀x∈S。
-
观察 f ( x ) f(x) f(x)与 f ( x ∗ ) + [ ∇ f ( x ∗ ) ] T ( x − x ∗ ) , ∀ x ∈ S f(x^*) + [\nabla f(x^*)]^T(x - x^*),\forall x \in \mathcal S f(x∗)+[∇f(x∗)]T(x−x∗),∀x∈S两者之间的大小关系。必然有:
其中不等式右侧描述:过[ x ∗ , f ( x ∗ ) ] [x^*,f(x^*)] [x∗,f(x∗)]点并与凸函数 f ( ⋅ ) f(\cdot) f(⋅)相切的直线。根据凸函数的定义,函数图像必然全部在切线上方。又根据上述条件,必然有:f ( x ∗ ) + [ ∇ f ( x ∗ ) ] T ( x − x ∗ ) ≥ f ( x ∗ ) f(x^*) + [\nabla f(x^*)]^T(x - x^*) \geq f(x^*) f(x∗)+[∇f(x∗)]T(x−x∗)≥f(x∗)。
f ( x ) ≥ f ( x ∗ ) + [ ∇ f ( x ∗ ) ] T ( x − x ∗ ) ≥ f ( x ∗ ) f(x) \geq f(x^*) + [\nabla f(x^*)]^T (x - x^*) \geq f(x^*) f(x)≥f(x∗)+[∇f(x∗)]T(x−x∗)≥f(x∗)
-
总上,对于 x ∈ S x \in \mathcal S x∈S,都有上述式子 f ( x ) ≥ f ( x ∗ ) f(x) \geq f(x^*) f(x)≥f(x∗)成立,因而 x ∗ x^* x∗是全局最优解。
必要性:已知某解 x ∗ x^* x∗是全局最优解。(反证法)证明:
- 假设 ∃ x ˉ ∈ S \exist \bar{x} \in \mathcal S ∃xˉ∈S,使得: [ ∇ f ( x ∗ ) ] T ( x ˉ − x ∗ ) < 0 [\nabla f(x^*)]^T(\bar{x} - x^*) < 0 [∇f(x∗)]T(xˉ−x∗)<0;
- 基于上述假设,以 x ∗ x^* x∗为起始,向 x ˉ \bar{x} xˉ方向移动一个较小距离 λ ⋅ ( x ˉ − x ∗ ) , λ ∈ ( 0 , 1 ) \lambda \cdot (\bar{x} - x^*),\lambda \in (0,1) λ⋅(xˉ−x∗),λ∈(0,1),观察函数值从 f ( x ∗ ) f(x^*) f(x∗)到 f [ x ∗ + λ ⋅ ( x ˉ − x ∗ ) ] f[x^* + \lambda \cdot (\bar{x} - x^*)] f[x∗+λ⋅(xˉ−x∗)]的变化情况。这里使用泰勒公式对 f [ x ∗ + λ ⋅ ( x ˉ − x ∗ ) ] f[x^* + \lambda \cdot (\bar{x} - x^*)] f[x∗+λ⋅(xˉ−x∗)]在 x ∗ x^* x∗处进行展开:
其中O ( ⋅ ) \mathcal O(\cdot) O(⋅)表示高阶无穷小。
f [ x ∗ + λ ⋅ ( x ˉ − x ∗ ) ] = f ( x ∗ ) + 1 1 ! ⋅ λ [ ∇ f ( x ∗ ) ] T ( x ˉ − x ∗ ) + O ( λ ∣ ∣ x ˉ − x ∗ ∣ ∣ ) λ ∈ ( 0 , 1 ) f[x^* + \lambda \cdot(\bar{x} - x^*)] = f(x^*) + \frac{1}{1 !} \cdot \lambda [\nabla f(x^*)]^T(\bar{x} - x^*) +\mathcal O(\lambda ||\bar{x} - x^*||) \quad \lambda \in (0,1) f[x∗+λ⋅(xˉ−x∗)]=f(x∗)+1!1⋅λ[∇f(x∗)]T(xˉ−x∗)+O(λ∣∣xˉ−x∗∣∣)λ∈(0,1)
整理得:
f [ x ∗ + λ ⋅ ( x ˉ − x ∗ ) ] − f ( x ∗ ) λ = [ ∇ f ( x ∗ ) ] T ( x ˉ − x ∗ ) + O ( λ ⋅ ∣ ∣ x ˉ − x ∗ ∣ ∣ ) λ \frac{f[x^* + \lambda \cdot (\bar{x} - x^*)] - f(x^*)}{\lambda} = [\nabla f(x^*)]^T(\bar{x} - x^*) + \frac{\mathcal O(\lambda \cdot ||\bar{x} - x^*||)}{\lambda} λf[x∗+λ⋅(xˉ−x∗)]−f(x∗)=[∇f(x∗)]T(xˉ−x∗)+λO(λ⋅∣∣xˉ−x∗∣∣)
当 λ ⇒ 0 \lambda \Rightarrow 0 λ⇒0时,等式右侧的符号由 [ ∇ f ( x ∗ ) ] T ( x ˉ − x ∗ ) [\nabla f(x^*)]^T(\bar{x} - x^*) [∇f(x∗)]T(xˉ−x∗)控制: < 0 <0 <0;等式左侧自然也 < 0 <0 <0:
关于高阶无穷小:O ( λ ⋅ ∣ ∣ x ˉ − x ∗ ∣ ∣ ) λ \begin{aligned}\frac{\mathcal O(\lambda \cdot ||\bar{x} - x^*||)}{\lambda}\end{aligned} λO(λ⋅∣∣xˉ−x∗∣∣)在λ ⇒ 0 \lambda \Rightarrow 0 λ⇒0时,分子趋于0 0 0的速度更快。因而lim λ ⇒ 0 O ( λ ⋅ ∣ ∣ x ˉ − x ∗ ∣ ∣ ) λ = 0 \begin{aligned}\mathop{\lim}\limits_{\lambda \Rightarrow 0} \frac{\mathcal O(\lambda \cdot ||\bar{x} - x^*||)}{\lambda} = 0\end{aligned} λ⇒0limλO(λ⋅∣∣xˉ−x∗∣∣)=0。
lim λ ⇒ 0 f [ x ∗ + λ ⋅ ( x ˉ − x ∗ ) ] − f ( x ∗ ) λ < 0 ⇒ lim λ ⇒ 0 f [ x ∗ + λ ⋅ ( x ˉ − x ∗ ) ] − f ( x ∗ ) < 0 \mathop{\lim}\limits_{\lambda \Rightarrow 0} \frac{f[x^* + \lambda \cdot (\bar{x} - x^*)] - f(x^*)}{\lambda} <0 \Rightarrow \mathop{\lim}\limits_{\lambda \Rightarrow 0} f[x^* + \lambda \cdot(\bar{x} - x^*)] - f(x^*) <0 λ⇒0limλf[x∗+λ⋅(xˉ−x∗)]−f(x∗)<0⇒λ⇒0limf[x∗+λ⋅(xˉ−x∗)]−f(x∗)<0
这意味着:存在一点 x ∗ + λ ⋅ ( x ˉ − x ∗ ) x^* + \lambda \cdot(\bar{x} - x^*) x∗+λ⋅(xˉ−x∗),其函数值 f [ x ∗ + λ ⋅ ( x ˉ − x ∗ ) ] < f ( x ∗ ) f[x^* + \lambda \cdot(\bar{x} - x^*)] < f(x^*) f[x∗+λ⋅(xˉ−x∗)]<f(x∗)。也就是说: x ∗ x^* x∗不是全局最优解。这与条件相矛盾,证毕。
关于凸优化问题最优性条件的几何解释
对上述最优性条件变换成如下形式:
x ∗ ∈ S is Optimal ⇔ − [ ∇ f ( x ∗ ) ] T x ∗ ≥ − [ ∇ f ( x ∗ ) ] T x ∀ x ∈ S x^* \in \mathcal S \text{ is Optimal } \Leftrightarrow - [\nabla f(x^*)]^T x^* \geq - [\nabla f(x^*)]^T x \quad \forall x \in \mathcal S x∗∈S is Optimal ⇔−[∇f(x∗)]Tx∗≥−[∇f(x∗)]Tx∀x∈S
根据凸集的支撑超平面定理,如果 − [ ∇ f ( x ∗ ) ] ≠ 0 -[\nabla f(x^*)] \neq 0 −[∇f(x∗)]=0,则可以找到以 x ∗ x^* x∗为边界点,并垂直于向量 − [ ∇ f ( x ∗ ) ] -[\nabla f(x^*)] −[∇f(x∗)]的超平面,使该超平面支撑凸集 S \mathcal S S。而 − [ ∇ f ( x ∗ ) ] -[\nabla f(x^*)] −[∇f(x∗)]作为负梯度方向,必然有: ∀ x ∈ S , s.t. − [ ∇ f ( x ∗ ) ] ( x − x ∗ ) ≤ 0 \forall x \in \mathcal S,\text{ s.t. }-[\nabla f(x^*)](x - x^*) \leq 0 ∀x∈S, s.t. −[∇f(x∗)](x−x∗)≤0。对应图像表示如下:
其中支撑超平面定理是凸集的自身性质。也就是说:向量− [ ∇ f ( x ∗ ) ] -[\nabla f(x^*)] −[∇f(x∗)]与向量x − x ∗ x -x^* x−x∗之间的夹角≥ 9 0 。 \geq 90^。 ≥90。恒成立。

个人深度思考:上述最优性条件成立建立在 − [ ∇ f ( x ∗ ) ] ≠ 0 -[\nabla f(x^*)] \neq 0 −[∇f(x∗)]=0的情况下,如果 − [ ∇ f ( x ∗ ) ] = 0 - [\nabla f(x^*)] =0 −[∇f(x∗)]=0时,有: ∀ x ∈ S , [ ∇ f ( x ∗ ) ] T ( x − x ∗ ) ≥ 0 \forall x \in \mathcal S,[\nabla f(x^*)]^T (x - x^*) \geq 0 ∀x∈S,[∇f(x∗)]T(x−x∗)≥0恒成立。也就是说:在凸集中的任意一点,都可以满足该条件。在迭代寻找最优解的过程中,如果 − [ ∇ f ( x ∗ ) ] = 0 -[\nabla f(x^*)] = 0 −[∇f(x∗)]=0,可能会选择错误的方向。
什么时候会出现这种情况:梯度消失的时候。也就是说:如果出现梯度消失的情况下,在迭代寻找最优解的过程中,可能会选择错误的方向。最终找到的最优解可能并不是凸集的某个边界点,而是某个内点。
当然,如果选择的点是内点并且目标函数结果又返回至较大的情况,此时的梯度又存在了,会继续重新收敛至最优解。这里只是描述出现的这种反弹现象。
几种特殊凸问题的最优性条件
无约束凸优化
无约束凸优化问题:在目标函数 f ( ⋅ ) f(\cdot) f(⋅)是凸函数的条件下, x ∈ R n x \in \mathbb R^n x∈Rn,关于 min f ( x ) \min f(x) minf(x)的最优性条件表示如下:
x ∗ is Optimal ⇔ ∇ f ( x ∗ ) = 0 x^* \text{ is Optimal } \Leftrightarrow \nabla f(x^*) = 0 x∗ is Optimal ⇔∇f(x∗)=0
如果将该问题带入凸优化问题最优性条件中,可以得到:
x ∗ is Optimal ⇔ [ ∇ f ( x ∗ ) ] T ( x − x ∗ ) ≥ 0 , ∀ x ∈ R n ⇔ ∇ f ( x ∗ ) = 0 x^* \text{ is Optimal } \Leftrightarrow [\nabla f(x^*)]^T(x - x^*) \geq 0,\forall x \in \mathbb R^n \Leftrightarrow \nabla f(x^*) = 0 x∗ is Optimal ⇔[∇f(x∗)]T(x−x∗)≥0,∀x∈Rn⇔∇f(x∗)=0
可以理解为: ∀ x ∈ R n \forall x \in \mathbb R^n ∀x∈Rn构成的向量 x − x ∗ x - x^* x−x∗均满足 [ ∇ f ( x ∗ ) ] T ( x − x ∗ ) ≥ 0 [\nabla f(x^*)]^T(x - x^*) \geq 0 [∇f(x∗)]T(x−x∗)≥0,那只有一种情况: ∇ f ( x ) \nabla f(x) ∇f(x)是零向量。
这里需要与上面描述的梯度消失的情况区分一下。上述的最优性条件必须满足可行域 S \mathcal S S是凸集。如果在 S \mathcal S S是凸集情况下, ∇ f ( x ∗ ) = 0 \nabla f(x^*) =0 ∇f(x∗)=0会导致无法找到 x ∗ x^* x∗位置下关于凸集 S \mathcal S S的支撑超平面;相反,在无约束凸优化问题中,对可行域 S \mathcal S S没有约束。
等式约束凸优化
等式约束的凸优化问题:在目标函数 f ( ⋅ ) f(\cdot) f(⋅)是凸函数的条件下,关于 min { f ( x ) ∣ A x = b } \min \{f(x) \mid \mathcal A x = b\} min{f(x)∣Ax=b}的最优性条件表示如下:
关于凸优化问题的等式约束函数是线性函数。
x ∗ is Optimal ⇔ ∃ μ , s.t. ∇ f ( x ∗ ) + A T μ = 0 , A x ∗ = 0 x^* \text{ is Optimal } \Leftrightarrow \exist \mu, \text{ s.t. } \nabla f(x^*) + \mathcal A^T \mu = 0,\mathcal A x^* = 0 x∗ is Optimal ⇔∃μ, s.t. ∇f(x∗)+ATμ=0,Ax∗=0
证明:
如果 x ∗ x^* x∗是全局最优解,必然有:
x ∗ is Optimal ⇔ [ ∇ f ( x ∗ ) ] T ( x − x ∗ ) ≥ 0 ∀ x : A x = b , A x ∗ = b x^* \text{ is Optimal } \Leftrightarrow [\nabla f(x^*)]^T(x - x^*) \geq 0 \quad \forall x:\mathcal Ax = b,\mathcal Ax^* = b x∗ is Optimal ⇔[∇f(x∗)]T(x−x∗)≥0∀x:Ax=b,Ax∗=b
根据 A x = A x ∗ = b \mathcal Ax = \mathcal Ax^* = b Ax=Ax∗=b,因而有: A ( x − x ∗ ) = b − b = 0 \mathcal A(x - x^*) = b - b =0 A(x−x∗)=b−b=0。记向量 d = x − x ∗ d = x - x^* d=x−x∗,从而有:
x ∗ is Optimal ⇔ [ ∇ f ( x ∗ ) ] T d ≥ 0 ∀ d : A d = 0 x^* \text{ is Optimal } \Leftrightarrow [\nabla f(x^*)]^T d \geq 0 \quad \forall d:\mathcal Ad = 0 x∗ is Optimal ⇔[∇f(x∗)]Td≥0∀d:Ad=0
很明显, A d = 0 \mathcal Ad =0 Ad=0是一个齐次线性方程组,可以将 d d d描述为: A x = 0 \mathcal Ax = 0 Ax=0解集中的一个解。即: d ∈ N ( A ) d \in \mathcal N(\mathcal A) d∈N(A):
其中 N ( A ) \mathcal N(\mathcal A) N(A)表示系数矩阵 A \mathcal A A的零空间。
x ∗ is Optimal ⇔ [ ∇ f ( x ∗ ) ] T d ≥ 0 ∀ d ∈ N ( A ) x^* \text{ is Optimal } \Leftrightarrow [\nabla f(x^*)]^T d \geq 0 \quad \forall d \in \mathcal N(\mathcal A) x∗ is Optimal ⇔[∇f(x∗)]Td≥0∀d∈N(A)
发现这样一个现象:如果 d ∈ N ( A ) d \in \mathcal N(\mathcal A) d∈N(A)那么 − d ∈ N ( A ) ⇒ − A d = 0 -d \in \mathcal N(\mathcal A) \Rightarrow -\mathcal Ad = 0 −d∈N(A)⇒−Ad=0,将 d , − d d,-d d,−d都带入上式中:
{ [ ∇ f ( x ∗ ) ] T d ≥ 0 [ ∇ f ( x ∗ ) ] T ( − d ) ≥ 0 ⇒ [ ∇ f ( x ∗ ) ] T d ≤ 0 \begin{cases} [\nabla f(x^*)]^Td \geq 0 \\ [\nabla f(x^*)]^T(-d) \geq 0 \Rightarrow [\nabla f(x^*)]^T d \leq 0 \end{cases} {[∇f(x∗)]Td≥0[∇f(x∗)]T(−d)≥0⇒[∇f(x∗)]Td≤0
也就是说:关于 [ ∇ f ( x ∗ ) ] T d [\nabla f(x^*)]^T d [∇f(x∗)]Td在可行域 d ∈ N ( A ) d \in \mathcal N(\mathcal A) d∈N(A)中只能取等:
x ∗ is Optimal ⇔ [ ∇ f ( x ∗ ) ] T d = 0 ∀ d ∈ N ( A ) x^* \text{ is Optimal } \Leftrightarrow [\nabla f(x^*)]^T d = 0 \quad \forall d \in \mathcal N(\mathcal A) x∗ is Optimal ⇔[∇f(x∗)]Td=0∀d∈N(A)
这意味着:向量 ∇ f ( x ∗ ) \nabla f(x^*) ∇f(x∗)与 N ( A ) \mathcal N(\mathcal A) N(A)中的任意解向量 d d d均是垂直关系,即向量 ∇ f ( x ∗ ) \nabla f(x^*) ∇f(x∗)与 N ( A ) \mathcal N(\mathcal A) N(A)垂直:
x ∗ is Optimal ⇔ ∇ f ( x ∗ ) ∈ N ( A ) ⊥ x^* \text{ is Optimal } \Leftrightarrow \nabla f(x^*) \in \mathcal N(\mathcal A)^{\bot} x∗ is Optimal ⇔∇f(x∗)∈N(A)⊥
对应图像表示如下:
其中 [ ∇ f ( x ∗ ) ] T d = ∥ ∇ f ( x ∗ ) ∥ ⋅ ∥ d ∥ ⋅ cos θ = 0 → cos θ = 0 [\nabla f(x^*)]^Td = \|\nabla f(x^*)\| \cdot \|d\| \cdot \cos \theta = 0\rightarrow \cos \theta = 0 [∇f(x∗)]Td=∥∇f(x∗)∥⋅∥d∥⋅cosθ=0→cosθ=0

因而 ∇ f ( x ∗ ) \nabla f(x^*) ∇f(x∗)必然能够表达为系数矩阵 A \mathcal A A行向量的线性组合。对应数学符号表示为:
这实际上就是 KKT \text{KKT} KKT条件在等式约束凸问题的具体化。后续有机会介绍~
x ∗ is Optimal ⇔ ∇ f ( x ∗ ) + A T μ = 0 x^* \text{ is Optimal } \Leftrightarrow \nabla f(x^*) + \mathcal A^T \mu = 0 x∗ is Optimal ⇔∇f(x∗)+ATμ=0
非负约束凸优化
基于非负约束的凸优化问题:在目标函数 f ( ⋅ ) f(\cdot) f(⋅)是凸函数的条件下,关于 min { f ( x ) ∣ x ≥ 0 } \min\{f(x) \mid x \geq 0\} min{f(x)∣x≥0}的最优性条件表示如下:
x ∗ is Optimal ⇔ ∇ f ( x ∗ ) i ⋅ x i ∗ = 0 x ∗ ≥ 0 ; ∇ f ( x ∗ ) ≥ 0 x^* \text{ is Optimal } \Leftrightarrow \nabla f(x^*)_i \cdot x_i^* = 0\quad x^* \geq 0;\nabla f(x^*) \geq 0 x∗ is Optimal ⇔∇f(x∗)i⋅xi∗=0x∗≥0;∇f(x∗)≥0
证明:依然根据凸优化问题的最优性条件,有:
其中 x ∗ x^* x∗作为可行域内的最优解,必然也满足: x ∗ ≥ 0 x^* \geq 0 x∗≥0
x ∗ is Optimal ⇔ [ ∇ f ( x ∗ ) ] T ( x − x ∗ ) ≥ 0 ∀ x ≥ 0 ; x ∗ ≥ 0 x^* \text{ is Optimal } \Leftrightarrow [\nabla f(x^*)]^T (x - x^*) \geq 0 \quad \forall x \geq 0;x^* \geq 0 x∗ is Optimal ⇔[∇f(x∗)]T(x−x∗)≥0∀x≥0;x∗≥0
将上式展开,整理有:
x ∗ is Optimal ⇔ [ ∇ f ( x ∗ ) ] T x ≥ [ ∇ f ( x ∗ ) ] T x ∗ ∀ x ≥ 0 ; x ∗ ≥ 0 x^* \text{ is Optimal } \Leftrightarrow [\nabla f(x^*)]^T x \geq [\nabla f(x^*)]^T x^* \quad \forall x \geq 0;x^* \geq 0 x∗ is Optimal ⇔[∇f(x∗)]Tx≥[∇f(x∗)]Tx∗∀x≥0;x∗≥0
观察上式: ∀ x ≥ 0 \forall x \geq 0 ∀x≥0,并满足: [ ∇ f ( x ∗ ) ] T x ≥ [ ∇ f ( x ∗ ) ] T x ∗ [\nabla f(x^*)]^T x \geq [\nabla f(x^*)]^T x^* [∇f(x∗)]Tx≥[∇f(x∗)]Tx∗,必然有:
解释:如果∇ f ( x ∗ ) \nabla f(x^*) ∇f(x∗)中存在某一个/若干个分量< 0 <0 <0,在执行线性运算[ ∇ f ( x ∗ ) ] T x [\nabla f(x^*)]^Tx [∇f(x∗)]Tx时,由于x x x可在x ≥ 0 x\geq 0 x≥0范围内任意取值,假设x x x中对应上述∇ f ( x ∗ ) \nabla f(x^*) ∇f(x∗)分量< 0 <0 <0的分量位置是+ ∞ +\infty +∞,那么[ ∇ f ( x ∗ ) ] T x [\nabla f(x^*)]^Tx [∇f(x∗)]Tx的结果必然是− ∞ -\infty −∞。这是可能发生的结果。但该结果可能不满足[ ∇ f ( x ∗ ) ] T x ≥ [ ∇ f ( x ∗ ) ] T x ∗ [\nabla f(x^*)]^T x \geq [\nabla f(x^*)]^T x^* [∇f(x∗)]Tx≥[∇f(x∗)]Tx∗。因此:∇ f ( x ∗ ) ≥ 0 \nabla f(x^*) \geq 0 ∇f(x∗)≥0必须成立。当x = 0 x = 0 x=0时,必然也满足:[ ∇ f ( x ∗ ) ] T x ∗ ≤ [ ∇ f ( x ∗ ) ] ⋅ 0 = 0 [\nabla f(x^*)]^Tx^* \leq [\nabla f(x^*)] \cdot 0 = 0 [∇f(x∗)]Tx∗≤[∇f(x∗)]⋅0=0
x ∗ is Optimal ⇔ { ∇ f ( x ∗ ) ≥ 0 ; x ∗ ≥ 0 [ ∇ f ( x ∗ ) ] T x ∗ ≤ 0 x^* \text{ is Optimal } \Leftrightarrow \begin{cases} \nabla f(x^*) \geq 0;x^* \geq 0 \\ [\nabla f(x^*)]^T x^* \leq 0 \end{cases} x∗ is Optimal ⇔{∇f(x∗)≥0;x∗≥0[∇f(x∗)]Tx∗≤0
继续观察上式:在 ∇ f ( x ∗ ) , x ∗ ≥ 0 \nabla f(x^*),x^* \geq 0 ∇f(x∗),x∗≥0情况下, [ ∇ f ( x ∗ ) ] T x ∗ ≤ 0 [\nabla f(x^*)]^T x^* \leq 0 [∇f(x∗)]Tx∗≤0。因此只有一种情况:
x ∗ is Optimal ⇔ { ∇ f ( x ∗ ) ≥ 0 ; x ∗ ≥ 0 [ ∇ f ( x ∗ ) ] T x ∗ = 0 x^* \text{ is Optimal } \Leftrightarrow \begin{cases} \nabla f(x^*) \geq 0;x^* \geq 0 \\ [\nabla f(x^*)]^T x^* = 0 \end{cases} x∗ is Optimal ⇔{∇f(x∗)≥0;x∗≥0[∇f(x∗)]Tx∗=0
这意味着:线性运算 [ ∇ f ( x ∗ ) ] T x [\nabla f(x^*)]^T x [∇f(x∗)]Tx过程执行加法运算的每一个分量 ∇ f ( x ∗ ) i ⋅ x i ( i = 1 , 2 , ⋯ , n ) \nabla f(x^*)_i \cdot x_i(i=1,2,\cdots,n) ∇f(x∗)i⋅xi(i=1,2,⋯,n)均为 0 0 0。
相反,如果存在某分量乘积结果 ∇ f ( x ∗ ) k ⋅ x k ∗ > 0 ( k ∈ { 1 , 2 , ⋯ , n } ) \nabla f(x^*)_k \cdot x_k^*> 0(k \in \{1,2,\cdots,n\}) ∇f(x∗)k⋅xk∗>0(k∈{1,2,⋯,n})最终的 [ ∇ f ( x ∗ ) ] T x [\nabla f(x^*)]^T x [∇f(x∗)]Tx结果必然 > 0 >0 >0,不满足上述条件。
证毕。
Reference \text{Reference} Reference:
最优化理论与方法-第四讲-凸优化问题
相关文章:

机器学习笔记之最优化理论与方法(五)凸优化问题(上)
机器学习笔记之最优化理论与方法——凸优化问题[上] 引言凸优化问题的基本定义凸优化定义:示例 凸优化与非凸优化问题的区分局部最优解即全局最优解凸优化问题的最优性条件几种特殊凸问题的最优性条件无约束凸优化等式约束凸优化非负约束凸优化 引言 本节将介绍凸优…...
在Windows10上编译grpc工程,得到protoc.exe和grpc_cpp_plugin.exe
grpc是google于2015年发布的一款跨进程、跨语言、开源的RPC(远程过程调用)技术。使用C/S模式,在客户端、服务端共享一个protobuf二进制数据。在点对点通信、微服务、跨语言通信等领域应用很广,下面介绍grpc在windows10上编译,这里以编译grpc …...

一些测试知识
希望能起到帮助,博主主页: https://blog.csdn.net/qq_57785602/category_12023254.html?spm1001.2014.3001.5482 软件测试理论 测试的依据: 需求,规格说明,模型,用户需求等 什么是软件测试 描述一种来…...

Socket交互的基本流程?
TCP socket通信过程图 什么是网络编程,网络编程就是编写程序使两台连联网的计算机相互交换数据。怎么交换数据呢?操作系统提供了“套接字”(socket)的组件我们基于这个组件进行网络通信开发。tcp套接字工作流程都以“打电话”来生…...

css 分割线中间带文字
效果图 代码块(自适应) <div class"line"><span class"text">我是文字</span></div>.line{height:0;border-top:1px solid #000;text-align:center;}.text{position:relative;top:-14px;background-color:#…...

会不会激发对modern c++的新兴趣
可变参数好像很厉害的样子,会节省很多手写代码,让编译器自动帮我们生成代码 template<typename Fun, typename...Args> void invoke(Fun&& fun, Args&&...args) { fun(std::forward<Args>(args)...); } 任意函数包装器…...

Nginx服务器如何配合Java开发项目
Nginx服务器如何才能配合好相关的编程语言进行服务器搭建呢?下面我们就来看看有关的技术如何融合。希望大家有所收获。 在进行Nginx服务器建设的时候有很多语言的应用,其中Java 开发的web项目就是很常见的。下面我们就看看Nginx服务器如何才能与Java编程…...
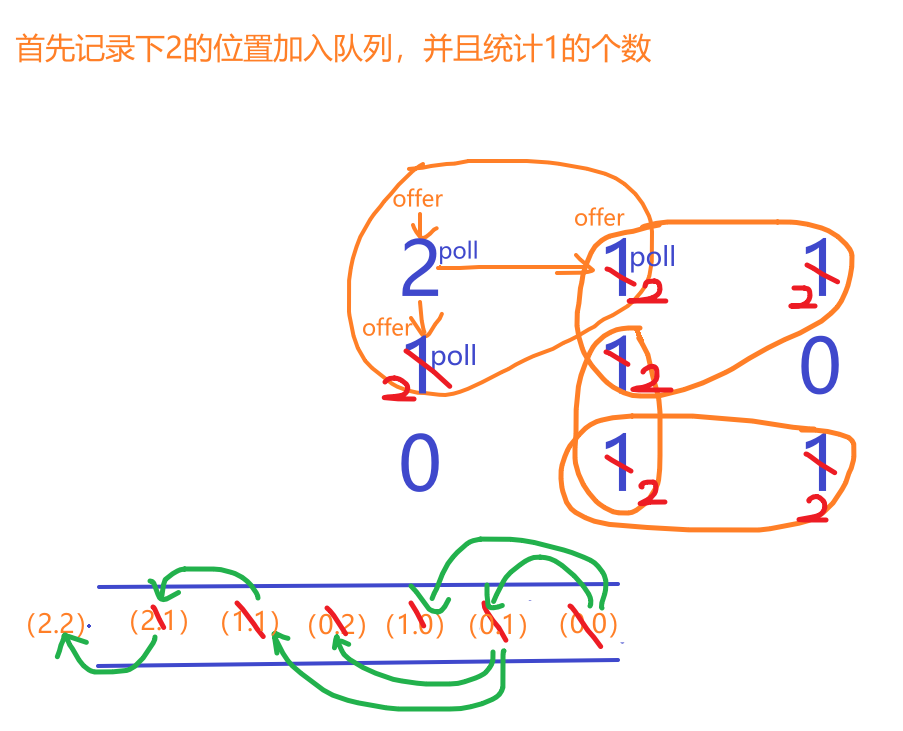
【LeetCode-中等题】994. 腐烂的橘子
文章目录 题目方法一:bfs层序遍历 题目 该题值推荐用bfs,因为是一层一层的感染,而不是一条线走到底的那种,所以深度优先搜索不适合 方法一:bfs层序遍历 广度优先搜索,就是从起点出发,每次都尝…...

K8s部署单机mysql
文章目录 一、K8s部署单机mysql1.1 说明1.2 不足 二、部署三、检查 一、K8s部署单机mysql 1.1 说明 定制配置数据存放在configMapmysql数据放在/opt/mysql目录下(/opt/mysql目录需要事先创建)root账号密码使用环境变量env服务暴露方式为nodePort,端口30336 1.2 不…...
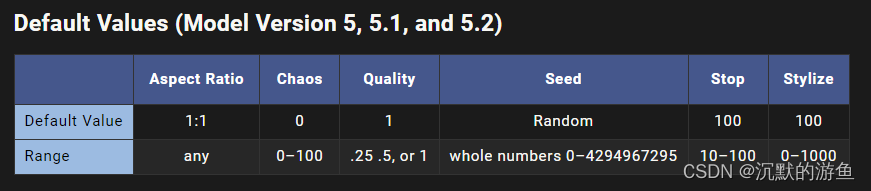
Midjourney学习(二)参数的基础
prompt的组成 prompt 可以由三部分组成, 第一部分是垫图部分,也就是一张网络图片 第二部分是文本描述内容 第三部分则是参数 参数列表 --aspect <value> 或者 --ar <value> 控制画面的比例,横竖比例 --version <value> -…...

Ubuntu安装Protobuf,指定版本
参考:https://github.com/protocolbuffers/protobuf#readme https://github.com/protocolbuffers/protobuf/blob/v3.20.3/src/README.md 其实官网的readme给的步骤很详细。 1.安装相关依赖 sudo apt-get install autoconf automake libtool curl make g unzip …...
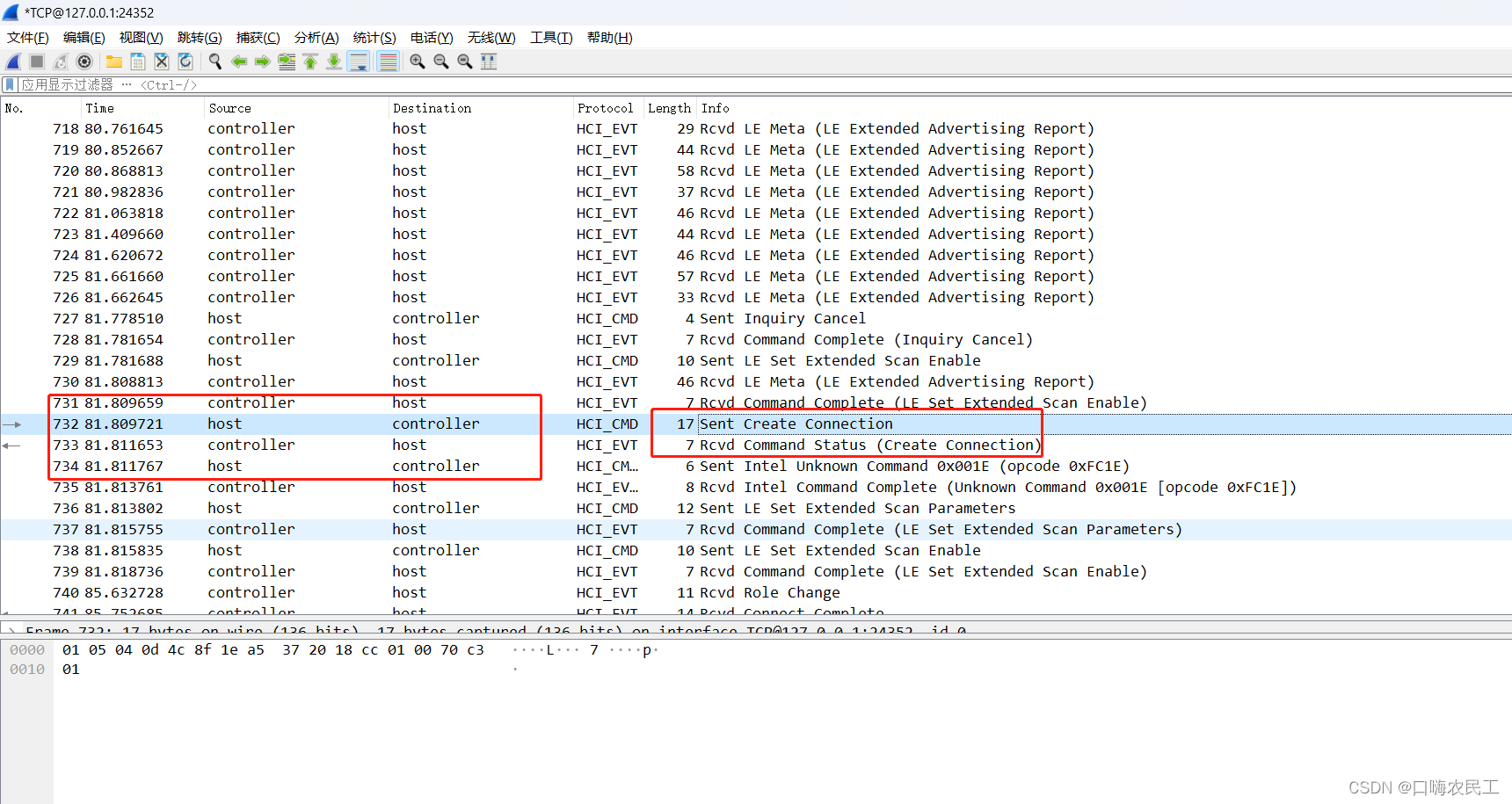
没有使用sniffer dongle在windows抓包蓝牙方法分享
网上很多文章都是介绍买一个sniffer dongle来抓蓝牙数据,嫌麻烦又费钱,目前找到一个好方法,不需要sniffer就可以抓蓝牙数据过程,现分享如下: (1)在我资源附件找到相关安装包或者查看如下链接 https://learn.microsoft.com/zh-cn/windows-hardware/drivers/bluetooth/testing-bt…...

解决Debian系统通过cifs挂载smb后,中文目录乱码问题
解决Debian系统通过cifs挂载smb后,中文目录乱码问题 //$smb_server/share /mnt/nas_share cifs credentials/root/.smbcredentials,iocharsetutf8 0 0默认通过以上命令挂载smb,但是在查看文件目录时,中文乱码 解决问题方式: de…...

springboot整合jquery实现前后端数据交互
一 实施逻辑 1.1 前端 <!doctype html> <html lang"en"><head><meta charset"UTF-8"><meta name"Generator" content"EditPlus"><meta name"Author" content""><meta n…...

TypeScript 中的类型检查实用函数
TypeScript 中的类型检查实用函数 文章目录 TypeScript 中的类型检查实用函数一、概述二、代码实现 一、概述 在前端开发中,我们经常需要判断变量的类型以进行相应的操作或处理。TypeScript 提供了基础的类型检查,但有时我们需要更复杂或更灵活的类型检…...

JavaScript中的事件委托(event delegation)
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ JavaScript事件委托⭐ 事件冒泡(Event Bubbling)⭐ 事件委托的优点⭐ 如何使用事件委托⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 记得点击上方或者右侧链接订阅本专栏哦 几何带你启…...

ubuntu OCR 脚本
1. 百度 PaddleOCR 介绍 2. 环境安装 pip install paddlepaddle -i https://pypi.tuna.tsinghua.edu.cn/simple # 进入 https://github.com/PaddlePaddle/PaddleOCR # 这里有个 requirements.txt pip install paddleocr -i https://mirror.baidu.com/pypi/simple pip instal…...
Go死码消除
概念: 死码消除(dead code elimination, DCE) 是一种编译器优化技术, 作用是在编译阶段去掉对程序运行结果没有任何影响的代码 和 逃逸分析[1],内联优化[2]并称为 Go编译器执行的三个重要优化 效果: 对于 const.go代码如下: package mainimport "fmt"func max(a, b i…...
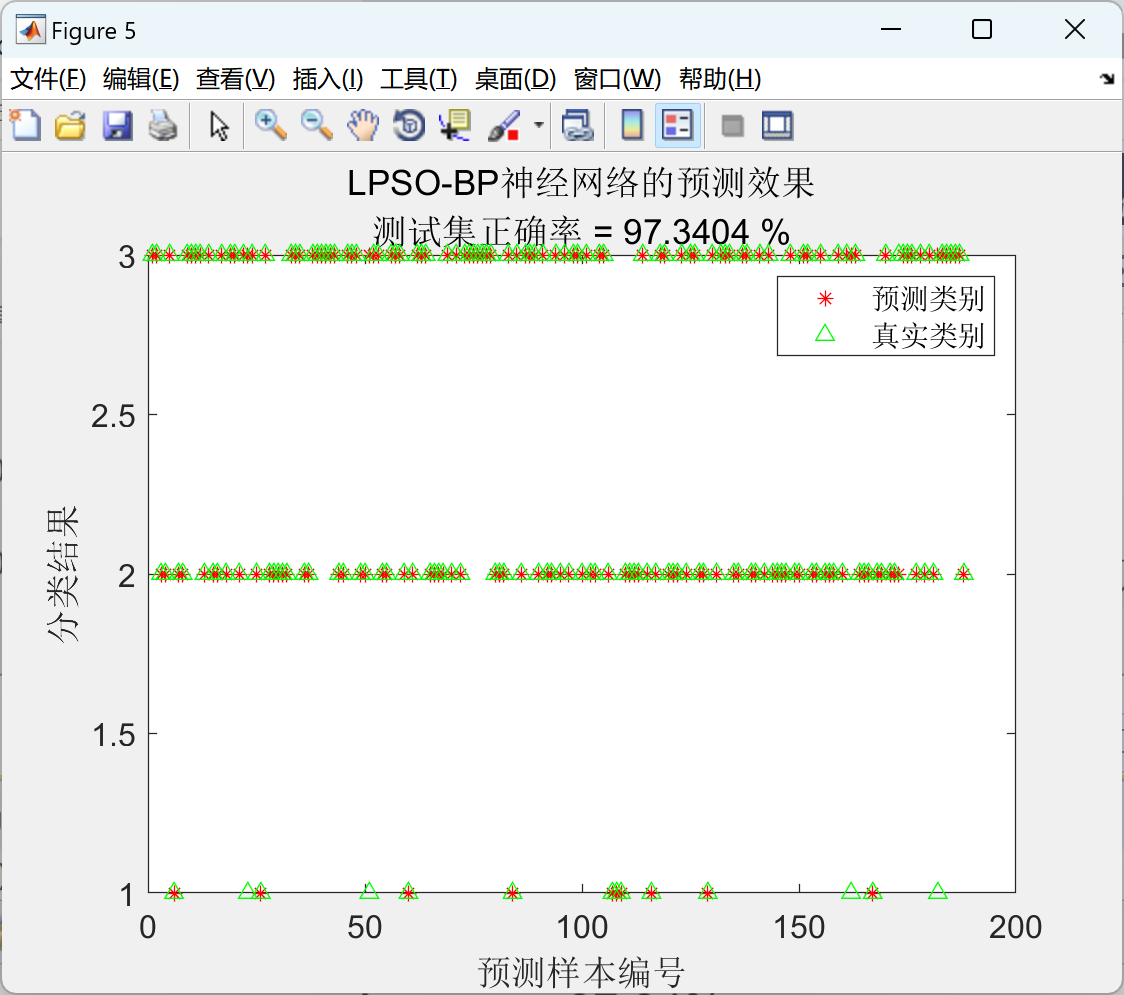
基于改进莱维飞行和混沌映射的粒子群优化BP神经网络分类研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
12. 自动化项目实战
目录 1. 登录测试 2. 测试首页的帖子列表数不为0 3. 帖子详情页校验 4. 发布帖子 5. 退出登录 自动化项目实施的基本流程如下图所示: 手工测试用例、自动化测试用例。 1. 登录测试 校验登录后主页显示的用户名称和登录时输入的用户名是否相等。 public class…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...

针对药品仓库的效期管理问题,如何利用WMS系统“破局”
案例: 某医药分销企业,主要经营各类药品的批发与零售。由于药品的特殊性,效期管理至关重要,但该企业一直面临效期问题的困扰。在未使用WMS系统之前,其药品入库、存储、出库等环节的效期管理主要依赖人工记录与检查。库…...
之(六) ——通用对象池总结(核心))
怎么开发一个网络协议模块(C语言框架)之(六) ——通用对象池总结(核心)
+---------------------------+ | operEntryTbl[] | ← 操作对象池 (对象数组) +---------------------------+ | 0 | 1 | 2 | ... | N-1 | +---------------------------+↓ 初始化时全部加入 +------------------------+ +-------------------------+ | …...

CppCon 2015 学习:REFLECTION TECHNIQUES IN C++
关于 Reflection(反射) 这个概念,总结一下: Reflection(反射)是什么? 反射是对类型的自我检查能力(Introspection) 可以查看类的成员变量、成员函数等信息。反射允许枚…...
