信息熵 条件熵 交叉熵 联合熵 相对熵(KL散度) 互信息(信息增益)
粗略版快速总结
条件熵 H ( Q ∣ P ) = 联合熵 H ( P , Q ) − H ( P ) 条件熵H(Q∣P)=联合熵H(P,Q)−H(P) 条件熵H(Q∣P)=联合熵H(P,Q)−H(P)
信息增益 I ( P , Q ) = H ( P ) − H ( P ∣ Q ) = H ( P ) + H ( Q ) − H ( P , Q ) 信息增益 I(P,Q)=H(P)−H(P∣Q)=H(P)+H(Q)-H(P,Q) 信息增益I(P,Q)=H(P)−H(P∣Q)=H(P)+H(Q)−H(P,Q),也就是Information Gain,互信息
KL散度(相对熵) K L ( P , Q ) = − H ( P ) + 交叉熵 C E ( P , Q ) KL(P,Q)=-H(P)+交叉熵CE(P,Q) KL(P,Q)=−H(P)+交叉熵CE(P,Q)
详细定义
如果一个样本是n类其中之一,也就是说target是onehot形式,例如三类那么target=[0,0,1],拿target=[0,0,1]来说就是 p 0 = 0 p_0=0 p0=0, p 1 = 0 p_1=0 p1=0, p 2 = 1 p_2=1 p2=1。写成表达式可以是 p i p_i pi,n=3
那么经过神经网络运算出来的Logits可能是在(-inf,inf)之间,那么一般会通过softmax归一化到(0,1)之间,这个归一化到(0,1)之间的数我们可以用 q i q_i qi来表示,当然对于上面有3类的例子来说,n=3
好了,既然明确了 p i p_i pi是第i个类的在(0,1)之间target, q i q_i qi是第i个类的logit归一化到(0,1)之间的结果,那么开始各种定义了
相对熵(KL散度)
K L ( P , Q ) = ∑ i ∈ [ 0 , n − 1 ] p i l o g p i q i KL(P,Q)=\sum _{i \in[0,n-1]}p_i log \frac{p_i}{q_i} KL(P,Q)=i∈[0,n−1]∑pilogqipi
交叉熵(CE Loss)
C E ( P , Q ) = − ∑ i ∈ [ 0 , n − 1 ] p i l o g q i K L ( P , Q ) = H ( P ) + C E ( P , Q ) CE(P,Q)=-\sum _{i \in[0,n-1]}p_i log q_i \\ KL(P,Q) = H(P)+CE(P,Q) CE(P,Q)=−i∈[0,n−1]∑pilogqiKL(P,Q)=H(P)+CE(P,Q)
来看一下Pytorch里的交叉熵是怎么实现的,手动验证下:
import torch
from torch import nn
import mathloss_f = nn.CrossEntropyLoss(reduction='mean')
output = torch.randn(2,3) #表示2个样本,3个类别
# target = torch.from_numpy(np.array([1, 0])).type(torch.LongTensor)
target = torch.LongTensor([0,2]) #表示label0和label2
loss = loss_f(output, target)print('CrossEntropy loss: ', loss)
print(f'reduction=none,所以可以看到每一个样本loss,输出为[{loss}]')def manual_cal(sample_index, target, output):#输入是样本下标sample_output = output[sample_index]sample_target = target[sample_index]x_class = sample_output[sample_target]sample_output_len = len(sample_output)log_sigma_exp_x = math.log(sum(math.exp(sample_output[i]) for i in range(sample_output_len)))sample_loss = -x_class + log_sigma_exp_xprint(f'交叉熵手动计算loss{sample_index}:{sample_loss}')return sample_lossfor i in range(2):manual_cal(i, target, output)# 如果nn.CrossEntropyLoss(reduction='mean')模式,刚好是手动计算的每个样本的loss取平均,最后输出的是一个值
# 如果nn.CrossEntropyLoss(reduction='none')模式,手动计算的loss0和loss1都会被列出来

(class torch.nn.CrossEntropyLoss(weight=None, size_average=None, ignore_index=-100, reduce=None, reduction=‘elementwise_mean’)
功能: 将输入经过softmax激活函数之后,再计算其与target的交叉熵损失。即该方法将nn.LogSoftmax()和 nn.NLLLoss()进行了结合。严格意义上的交叉熵损失函数应该是nn.NLLLoss()。

补充:交叉熵损失(cross-entropy Loss) 又称为对数似然损失(Log-likelihood Loss)、对数损失;二分类时还可称之为逻辑斯谛回归损失(Logistic Loss)。交叉熵损失函数表达式为 L = - sigama(y_i * log(x_i))。pytroch这里不是严格意义上的交叉熵损失函数(下面会详细解释,pytorch中交叉熵不够严格主要是因为只能接受one hot),而是先将input经过softmax激活函数,将向量“归一化”成概率形式,然后再与target计算严格意义上交叉熵损失。 在多分类任务中,经常采用softmax激活函数+交叉熵损失函数,因为交叉熵描述了两个概率分布的差异,然而神经网络输出的是向量,并不是概率分布的形式。所以需要softmax激活函数将一个向量进行“归一化”成概率分布的形式,再采用交叉熵损失函数计算loss。 再回顾PyTorch的CrossEntropyLoss(),官方文档中提到时将nn.LogSoftmax()和 nn.NLLLoss()进行了结合,nn.LogSoftmax() 相当于激活函数 , nn.NLLLoss()是损失函数;
来感受一下交叉熵取值的妙处:当 q i q_i qi很接近1时, − l o g q i -logq_i −logqi很接近0,如果此时 p i p_i pi是1,这时候整体loss会很小;当 q i q_i qi很接近0时, − l o g q i -logq_i −logqi很大, p i p_i pi是1,这时候整体loss会很大。所以 p i p_i pi就是筛选的功能,在Pytorch中CrossEntropyLoss等于LogSoftmax和NLLLoss的结合:LogSoftmax是上面公式里的 l o g ( e x p ( x [ c l a s s ] ) ∑ j e x p ( x [ j ] ) ) log(\frac{exp(x[class])}{\sum_jexp(x[j])}) log(∑jexp(x[j])exp(x[class])),实现了整个 l o g q i logq_i logqi的效果;NLLLoss就是给前面加了一个负号。所以在torch中的CrossEntropy = NLLLoss(LogSoftmax)
pytorch中交叉熵不够严格主要是因为只能接受one hot,也就是说torch中的target只能明确指明是哪个target,而不是上面公式 p i p_i pi是(0,1)之间,所以在Pytorch中还保留了KLDivLoss这个loss来接受广泛的取值:
import torch.nn.functional as F
import torch
import torch.nn as nn
# nn.CrossEntropyLoss() 和 KLDivLoss 关系y_pred = torch.tensor([[10.0, 0.0, -10.0], [8.0, 8.0, 8.0]])
y_true = torch.tensor([0, 2])
ce = nn.CrossEntropyLoss(reduction="none")(y_pred, y_true)
print(ce)
'''
输出shape是2,tensor([4.5418e-05, 1.0986e+00])
'''# NLLLoss要求target只能是第几类下标,例如[0,2]表示[label0,label2],转成onehot就是[[1,0,0],[0,0,1]]
nll_log_softmax = nn.NLLLoss(reduction="none")(F.log_softmax(y_pred, dim=-1), y_true)
print(nll_log_softmax)
'''
输出shape是2,tensor([4.5418e-05, 1.0986e+00])
'''one_hot = F.one_hot(y_true) #将第几类的下标转换成onehot形式,例如输入[0,2]表示[label0,label2],输出onehot就是[[1,0,0],[0,0,1]]
'''
# KLDivLoss要求target为float形式编码,one_hot是longtensor,所以要one_hot.float();如果是普通的logics,要过一下softmax# KLDivLoss也要求Logits经过LogSoftmax激活。LogSoftmax会把(-inf,inf)的Logits映射到(0,1)再映射到(-inf,0):当用NLLLoss时,刚好多个负号loss变成(0,inf);当用KLDivLoss时,刚好多个熵。回顾klLoss的公式 p_i*log(p_i/q_i),其中p_i是(0,1)范围内的targets
q_i是将logits映射到(0,1)范围内的结果,所以p_i和q_i都是(0,1)之间
KLDivLoss这个函数的特点就是把log(q_i)这一步扔给输入自己算,这个函数管的只是p_i*log(p_i)-p_i*inputNLLLoss这个函数的特点就是把p_i*log(p_i)也没了,只有-p_i*input,所以和LogSoftmax组合起来是CE
'''kl = nn.KLDivLoss(reduction="none")(F.log_softmax(y_pred, dim=-1), one_hot.float())
print(kl) #输出shape是2*3
'''
tensor([[4.5418e-05, 0.0000e+00, 0.0000e+00],[0.0000e+00, 0.0000e+00, 1.0986e+00]])
'''a = F.softmax(torch.randn(2,3))
print(nn.KLDivLoss(reduction="none")(torch.log(a), a))
'''
输出是
tensor([[0., 0., 0.],[0., 0., 0.]])回顾klLoss的公式 p_i*log(p_i/q_i),其中p_i是(0,1)范围内的targets
q_i是将logits映射到(0,1)范围内的结果,所以p_i和q_i都是(0,1)之间
KLDivLoss这个函数的特点就是把log(q_i)这一步扔给输入自己算,这个函数管的只是p_i*log(p_i)-p_i*inputNLLLoss这个函数的特点就是把p_i*log(p_i)也没了,只有-p_i*input,所以和LogSoftmax组合起来是CE
'''
为什么既有 KL 散度又有交叉熵?在信息论中,熵的意义是对 𝑃
事件的随机变量编码所需的最小字节数,KL 散度的意义是**“额外所需的编码长度”如果我们使用 𝑄的编码来表示 𝑃**,交叉熵指的是当你使用 𝑄作为密码来表示 𝑃 是所需要的 “平均的编码长度”。但是在机器学习评价两个分布之间的差异时,由于分布 𝑃 会是给定的,所以此时 KL 散度和交叉熵的作用其实是一样的,而且因为交叉熵少算一项,更加简单,所以选择交叉熵会更好。
Label Smoothing
Label Smoothing是一种防止网络过拟合的手段,在Pytorch的CrossEntropy中已经自带了这个参数,下图截自Hinton的论文When Does Label Smoothing Help? 从公式来看只把我们上面说的label/target做了一个衰减,更多细节可以参考https://blog.csdn.net/taoqick/article/details/121717218 :

联合熵
H ( P , Q ) = − ∑ i ∈ [ 0 , n − 1 ] P ( p i , q i ) l o g P ( p i , q i ) H(P,Q)=-\sum _{i \in[0,n-1]}P(p_i,q_i)logP(p_i,q_i) H(P,Q)=−i∈[0,n−1]∑P(pi,qi)logP(pi,qi)
条件熵
注意下面 P ( q i ∣ p i ) P(q_i|p_i) P(qi∣pi)表示 p i p_i pi和 q i q_i qi对应变量的条件概率, P ( p i , q i ) P(p_i,q_i) P(pi,qi)表示 p i p_i pi和 q i q_i qi对应变量的联合概率,写成这样只是为了简化但不够严谨。
H ( Q ∣ P ) = ∑ i ∈ [ 0 , n − 1 ] p i H ( Q ∣ P = p i ) H ( Q ∣ P ) = − ∑ i ∈ [ 0 , n − 1 ] p i ∗ P ( q i ∣ p i ) l o g P ( q i ∣ p i ) H ( Q ∣ P ) = − ∑ i ∈ [ 0 , n − 1 ] P ( p i , q i ) l o g P ( q i ∣ p i ) H(Q|P)=\sum _{i \in[0,n-1]}p_iH(Q|P=p_i) \\ H(Q|P)=-\sum _{i \in[0,n-1]}p_i*P(q_i|p_i)logP(q_i|p_i) \\ H(Q|P)=-\sum _{i \in[0,n-1]}P(p_i,q_i)logP(q_i|p_i) H(Q∣P)=i∈[0,n−1]∑piH(Q∣P=pi)H(Q∣P)=−i∈[0,n−1]∑pi∗P(qi∣pi)logP(qi∣pi)H(Q∣P)=−i∈[0,n−1]∑P(pi,qi)logP(qi∣pi)
上面就解释了为啥log里面是条件,外面是联合,更进一步地把里面也展开
H ( Q ∣ P ) = − ∑ i ∈ [ 0 , n − 1 ] P ( p i , q i ) l o g P ( q i ∣ p i ) H ( Q ∣ P ) = − H ( P , Q ) − ∑ i ∈ [ 0 , n − 1 ] P ( p i , q i ) l o g P ( p i ) H ( Q ∣ P ) = − H ( P , Q ) + H ( P ) H(Q|P)=-\sum _{i \in[0,n-1]}P(p_i,q_i)logP(q_i|p_i) \\ H(Q|P)=-H(P,Q)-\sum _{i \in[0,n-1]}P(p_i,q_i)logP(p_i) \\ H(Q|P)=-H(P,Q)+H(P) H(Q∣P)=−i∈[0,n−1]∑P(pi,qi)logP(qi∣pi)H(Q∣P)=−H(P,Q)−i∈[0,n−1]∑P(pi,qi)logP(pi)H(Q∣P)=−H(P,Q)+H(P)
至于熵为什么是这个定义请参考 为什么信息熵要定义成 − Σ p ∗ l o g ( p ) -Σp*log(p) −Σp∗log(p)?(https://blog.csdn.net/taoqick/article/details/72852255)。简单来说就是-log§就是信息量,单位用比特表示,例如中国队夺世界杯的信息量远比法国队夺世界杯信息量大。把一个系统里所有的-log§再乘以p就是熵,表示所有信息量加权平均,或者说熵就是信息量的数学期望
还有3个重要结论:
-
最小化交叉熵和极大似然本质上是一样的,更多推导参考:最小化交叉熵损失与极大似然 - 知乎(https://zhuanlan.zhihu.com/p/51099880)
-
为什么分类问题用相对熵不用MSE,原因之一是求解时相对熵的梯度下降更快一些,这样可以实现错误越大,下降的越快的效果,更多推导请参考: 分类问题中为什么用交叉熵而不用MSE KL散度和交叉熵的关系_taoqick的专栏-CSDN博客_mse和交叉熵 (https://blog.csdn.net/taoqick/article/details/102621605)
-
李航老师书里说的最大熵模型是条件熵最大化,想法就是某些知识已经先验知道了,剩下的随机变量尽量等概率随机,这样条件熵最大。学习概率模型时,在满足约束(特征函数)的所有的可能的概率分布中,熵最大的模型就是最大的模型。最大熵模型是判别式模型。
更多推导请参考李航老师的书和数学之美。
相关文章:

信息熵 条件熵 交叉熵 联合熵 相对熵(KL散度) 互信息(信息增益)
粗略版快速总结 条件熵 H ( Q ∣ P ) 联合熵 H ( P , Q ) − H ( P ) 条件熵H(Q∣P)联合熵H(P,Q)−H(P) 条件熵H(Q∣P)联合熵H(P,Q)−H(P) 信息增益 I ( P , Q ) H ( P ) − H ( P ∣ Q ) H ( P ) H ( Q ) − H ( P , Q ) 信息增益 I(P,Q)H(P)−H(P∣Q)H(P)H(Q)-H(P,Q) 信息…...

Fiddler Response私人订制
在客户端接口的测试中,我们经常会需要模拟各种返回状态或者特定的返回值,常见的是用Fiddler模拟各种请求返回值场景,如重定向AutoResponder、请求拦截修改再下发等等。小编在近期的测试中遇到的一些特殊的请求返回模拟的测试场景,…...
【德哥说库系列】-ASM管理Oracle 19C单实例部署
📢📢📢📣📣📣 哈喽!大家好,我是【IT邦德】,江湖人称jeames007,10余年DBA及大数据工作经验 一位上进心十足的【大数据领域博主】!😜&am…...
手写一个简单爬虫--手刃豆瓣top250排行榜
#拿到页面面源代码 request #通过re来提取想要的有效信息 re import requests import re url"https://movie.douban.com/top250"headers{"user-agent":"Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/11…...
【word密码】如何限制word文件中部分内容?
Word文件中有一部分内容不想他人编辑,我们可以设置限制编辑,可以对一部分内容设置限制编辑,具体方法如下: 我们将需要将可以编辑的地方选中,然后打开限制编辑功能 然后勾选限制编辑设置界面中的【限制编辑】和【每个人…...

spring 自定义类型转换-ConverterRegistry
1背景介绍 一个应用工程里面,一遍会涉及到很多的模型转换,如DTO模型转DO模型,DO模型转DTO, 或者Request转DTO模型,总的来说,维护起来还是相对比较复杂。每涉及一个转换都需要重新写对应类的get或者set方法,…...

springboot实现发送短信验证码
目录 一、选择并注册短信服务提供商: 二、添加依赖: 三、配置短信服务信息: 四、编写发送短信验证码的方法: 五、调用发送短信验证码的方法: 一、选择并注册短信服务提供商: 1、选择一个可靠的短信服…...

2024王道408数据结构P144 T18
2024王道408数据结构P144 T18 思考过程 首先还是先看题目的意思,让我们在中序线索二叉树里查找指定结点在后序的前驱结点,这题有一点难至少对我来说…我讲的不清楚理解一下我做的也有点糊涂。在创建结构体时多两个变量ltag和rtag,当ltag0时…...

在windows下安装配置skywalking
1.下载地址 Downloads | Apache SkyWalkinghttp://skywalking.apache.org/downloads/ 2.文件目录说明 将文件解压后,可看到agent和bin目录: Agent:作为探针,安装在服务器端,进行数据采集和上报。 Config:…...
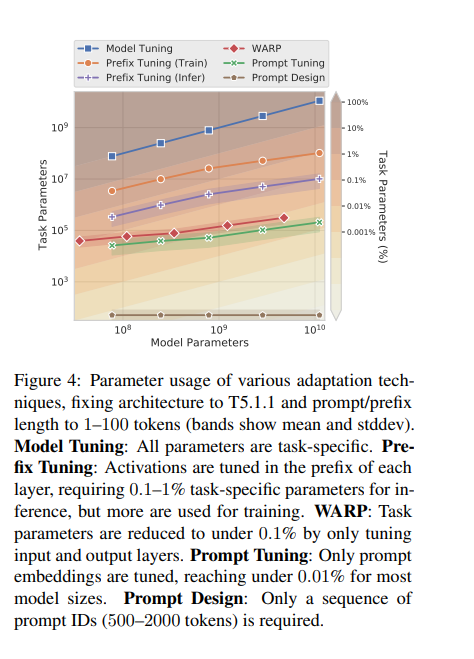
关于大模型参数微调的不同方法
Adapter Tuning 适配器模块(Adapter Moudle)可以生成一个紧凑且可扩展的模型;每个任务只需要添加少量可训练参数,并且可以在不重新访问之前任务的情况下添加新任务。原始网络的参数保持不变,实现了高度的参数共享 Pa…...
)
方法的引用第一版(method reference)
1、体验方法引用 在使用Lambda表达式的时候,我们实际上传递进去的代码就是一种解决方案:拿参数做操作那么考虑一种情况:如果我们在Lanbda中所指定的操作方案,已经有地方存在相同方案,那是否还有必要再重复逻辑呢&#…...

Android DataBinding 基础入门(学习记录)
目录 一、DataBinding简介二、findViewById 和 DataBinding 原理及优缺点1. findViewById的优缺点2. DataBinding的优缺点 三、Android mvvm 之 databinding 原理1. 简介和三个主要的实体DataViewViewDataBinding 2.三个功能2.1. rebind 行为2.2 observe data 行为2.3 observe …...

spring 错误百科
一、使用Spring出错根源 1、隐式规则的存在 你可能忽略了 Sping Boot 中 SpringBootApplication 是有一个默认的扫描包范围的。这就是一个隐私规则。如果你原本不知道,那么犯错概率还是很高的。类似的案例这里不再赘述。 2、默认配置不合理 3、追求奇技淫巧 4、…...
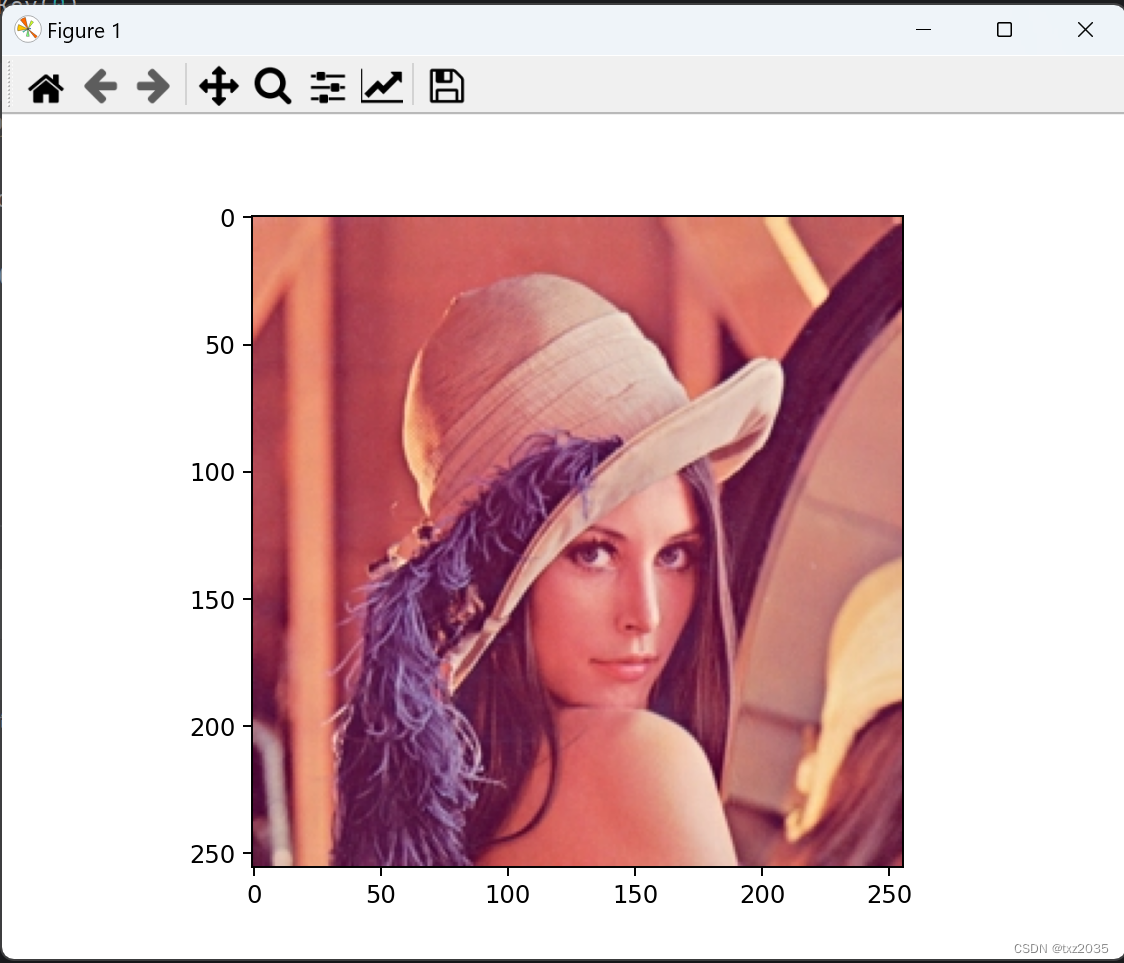
OpenCV基本操(IO操作,读取、显示、保存)
图像的IO操作,读取和保存方法 1.1 API cv.imread()参数: 要读取的图像 读取图像的方式: cv.IMREAD*COLOR:以彩色模式加载图像,任何图像的图像的透明度都将被忽略。这是默认参数 标志: 1 cv.IMREAD*GRAYSCALE :以…...

1.快速搭建Flask项目
一.Pear Admin Flask 官网文档:http://www.pearadmin.com/doc/index.html 1.1下载安装 # 下 载 git clone https://gitee.com/pear-admin/pear-admin-flask# 安 装 pip install -r requirements.txt1.2修改配置 applications下的config.py docker运行的修改dockerdata/conf…...

编程题四大算法思想(三)——贪心法:找零问题、背包问题、任务调度问题、活动选择问题、Prim算法
文章目录 贪心法找零问题(change-making problem)贪心算法要求基本思想适合求解问题的特征 背包问题0/1背包问题0/1背包问题——贪心法 分数背包问题 任务调度问题活动选择问题活动选择——贪心法最早结束时间优先——最优性证明 Prim算法 贪心法 我在当…...
core dump管理在linux中的前世今生
目录 一、什么是core dump? 二、coredump是怎么来的? 三、怎么限制coredump文件的产生? ulimit 半永久限制 永久限制 四、从源码分析如何对coredump文件的名字和路径管理 命名 管理 一些问题的答案 1、为什么新的ubuntu不能产生c…...

Springboot整合knife4j配置swagger教程-干货
开启swagger文档,直接上教程。 第一步:引入依赖 <!--swagger 依赖--><dependency><groupId>com.github.xiaoymin</groupId><artifactId>knife4j-spring-boot-starter</artifactId><version>3.0.3</version></d…...

C++ 中的 Pimpl 惯用法
C 中的 Pimpl 惯用法 介绍 Pimpl(Pointer to Implementation)是一种常见的 C 设计模式,用于隐藏类的实现细节,从而减少编译依赖和提高编译速度。本文将通过一个较为复杂的例子,展示如何使用智能指针(如 s…...

【个人博客系统网站】统一处理 · 拦截器
【JavaEE】进阶 个人博客系统(2) 文章目录 【JavaEE】进阶 个人博客系统(2)1. 统一返回格式处理1.1 统一返回类common.CommonResult1.2 统一返回处理器component.ResponseAdvice 2. 统一异常处理3. 拦截器实现3.1 全局变量SESSI…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...
