三种常用盒子布局的方法
在Vue中,可以使用各种CSS布局属性和技巧来设置盒子的布局。以下是一些常用的方法:
1.使用Flexbox布局:在包含盒子的父元素上设置
display: flex,然后可以使用flex-direction、justify-content和align-items等属性来控制盒子的布局。
<div class="container"><div class="box">盒子1</div><div class="box">盒子2</div><div class="box">盒子3</div>
</div>.container {display: flex;flex-direction: row; /* 设置为水平布局 */justify-content: space-between; /* 在容器中均匀分布盒子 */
}.box {/* 盒子样式设置 */
}2.使用CSS Grid布局:在包含盒子的父元素上设置
display: grid,然后通过设置grid-template-columns和grid-template-rows来定义网格布局。
<div class="container"><div class="box">盒子1</div><div class="box">盒子2</div><div class="box">盒子3</div>
</div>.container {display: grid;grid-template-columns: repeat(3, 1fr); /* 3列网格 */grid-gap: 10px; /* 设置盒子之间的间距 */
}.box {/* 盒子样式设置 */
}
3.使用CSS定位布局:使用
position属性和top、left、right和bottom等属性将每个盒子定位到适当的位置。
<div class="container"><div class="box" style="position: absolute; top: 0; left: 0;">盒子1</div><div class="box" style="position: absolute; top: 0; right: 0;">盒子2</div><div class="box" style="position: absolute; bottom: 0; left: 0;">盒子3</div>
</div>.container {position: relative; /* 设置容器为相对定位 */
}.box {/* 盒子样式设置 */
}这只是一些常见的布局方法,实际上有很多其他的方式可以进行盒子的布局。你可以根据具体需求选择适合的方法来设置盒子的布局。
相关文章:

三种常用盒子布局的方法
在Vue中,可以使用各种CSS布局属性和技巧来设置盒子的布局。以下是一些常用的方法: 1.使用Flexbox布局:在包含盒子的父元素上设置display: flex,然后可以使用flex-direction、justify-content和align-items 等属性来控制盒子的布局…...
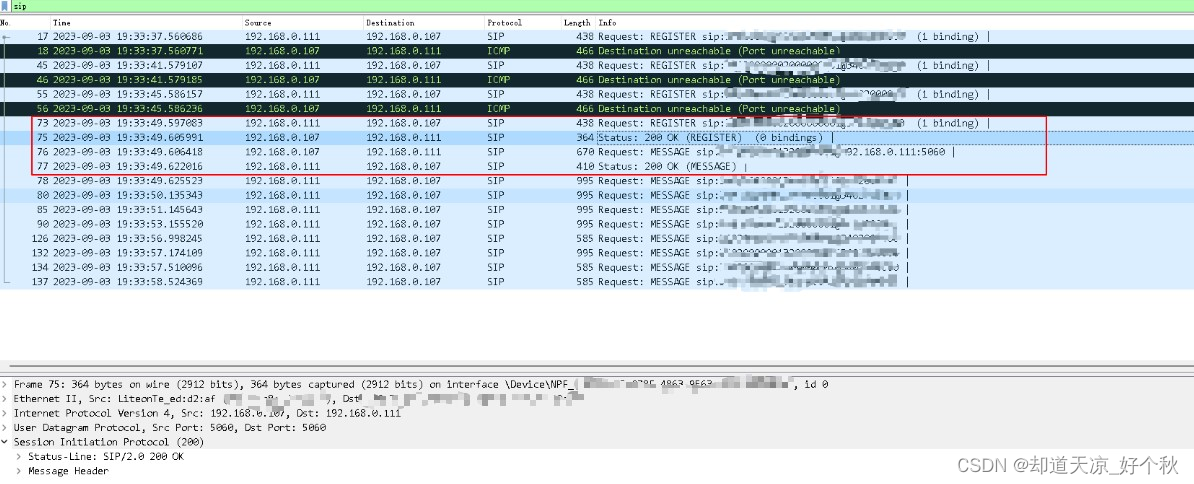
GB28181学习(二)——注册与注销
概念 使用REGISTER方法进行注册和注销;注册和注销应进行认证,认证方式应支持数字摘要认证方式,高安全级别的宜支持数字证书认证;注册成后,SIP代理在注册过期时间到来之前,应向注册服务器进行刷新注册&…...
【Linux】线程安全-信号量
文章目录 信号量原理信号量保证同步和互斥的原理探究信号量相关函数初始化信号量函数等待信号量函数释放信号量函数销毁信号量函数 信号量实现生产者消费者模型 信号量原理 信号量的原理:资源计数器 PCB等待队列 函数接口 资源计数器:对共享资源的计…...
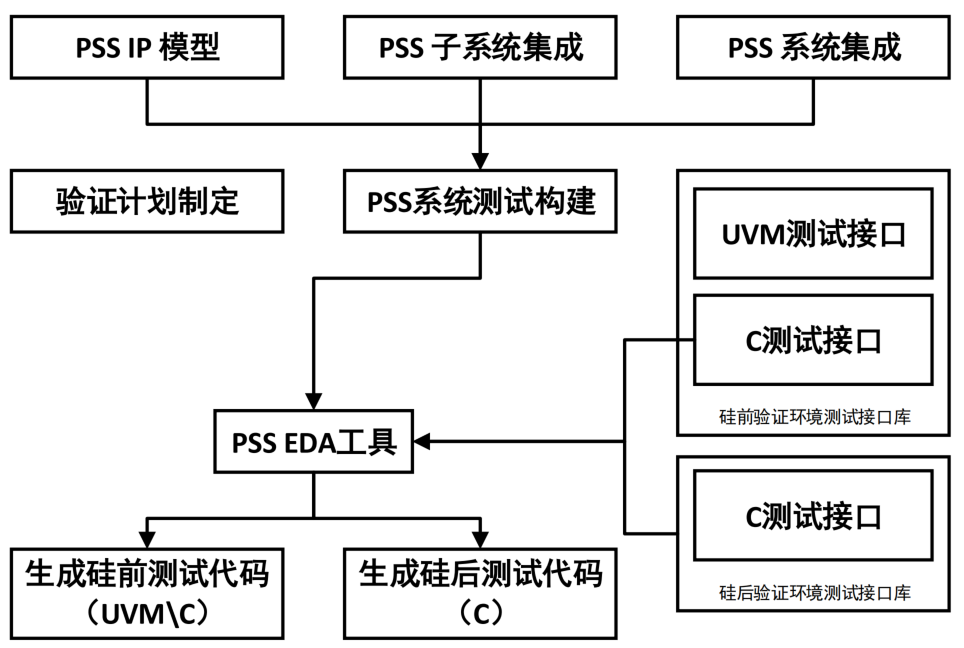
数字IC验证——PSS可移植测试用例
PSS是Accellera组织定义的测试用例生成规范,其思想是定义一个抽象模型,EDA工具可以从中生成适用于每个设计层次结构和每个验证平台的测试,即PSS定义了统一的测试场景,而场景的使用可以横跨不同验证层次和配置。 这种特性决定了PSS…...
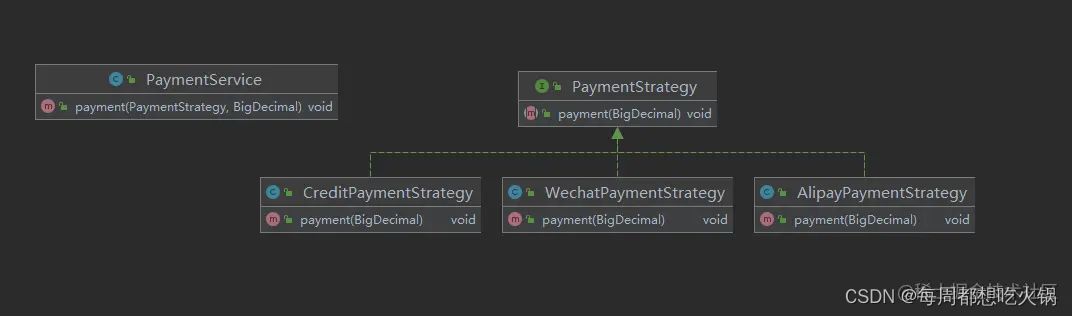
java设计模式---策略模式
策略模式的定义 策略设计模式是一种行为设计模式。当在处理一个业务时,有多种处理方式,并且需要再运行时决定使哪一种具体实现时,就会使用策略模式。 策略模式的类图: 策略模式的实现 在支付业务中,有三种付款方式&…...

5-redis集群搭建安装
1.先决条件 1.1.OS基础配置 CentOS为了能够正常安装redis,需要对CentOS进行常规的一些基础配置,主要有:关闭防火墙与selinux,设置主机名,配置虚拟机IP地址使其能够与外网ping通,配置IP地址与主机名映射,配置yum源。具体配置参见: Linux常规基础配置_小黑要上天的博客…...

(数字图像处理MATLAB+Python)第十一章图像描述与分析-第七、八节:纹理描述和其他描述
文章目录 一:纹理描述(1)联合概率矩阵法A:定义B:基于联合概率矩阵的特征C:程序 (2)灰度差分统计法A:定义B:描述图像特征的参数 (3)行程…...

MySQL提权
参考: mysql提权篇 | Wh0ales Blog MySQL 提权方法整理 - Geekbys Blog MySQL_UDF提权漏洞复现-云社区-华为云 MYSQL UDF手动提权及自动化工具使用_udf提权工具_小直789的博客-CSDN博客 MySQL提权的三种方法 - FreeBuf网络安全行业门户 ......
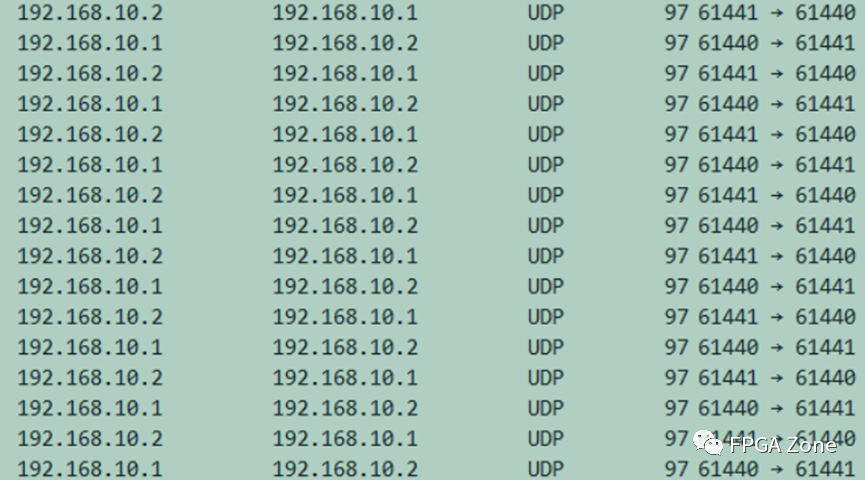
FPGA优质开源项目 – UDP万兆光纤以太网通信
本文开源一个FPGA项目:UDP万兆光通信。该项目实现了万兆光纤以太网数据回环传输功能。Vivado工程代码结构和之前开源的《UDP RGMII千兆以太网》类似,只不过万兆以太网是调用了Xilinx的10G Ethernet Subsystem IP核实现。 下面围绕该IP核的使用、用户接口…...
如何中mac上安装多版本python并配置PATH
摘要 mac 默认安装的python是 python3,但是如果我们需要其他python版本时,该怎么办呢? 例如:需要python2 版本,如果使用homebrew安装会提示没有python2。同时使用python --version 会发现commond not found。 所以本…...
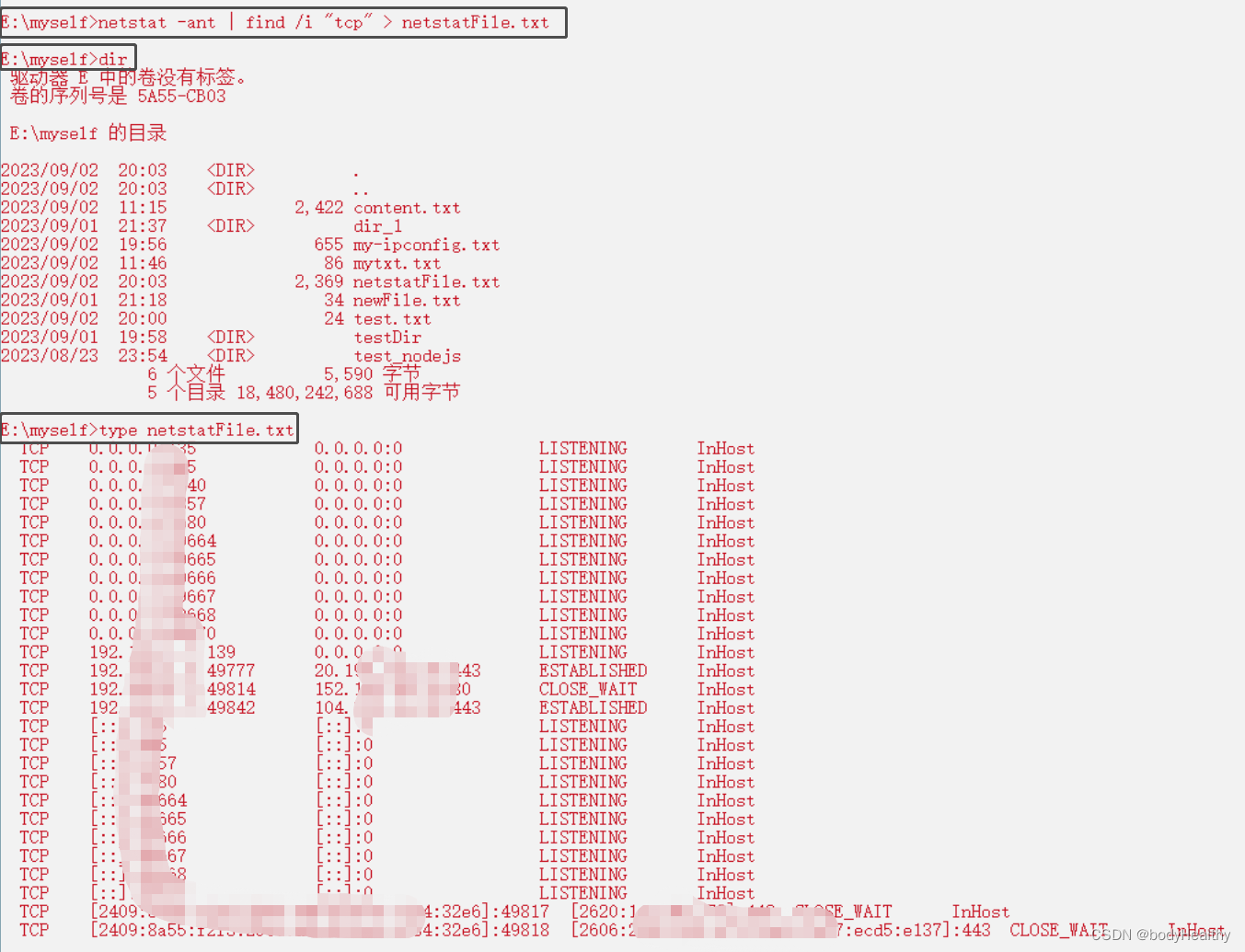
window 常用基础命令
0、起步 0-1) 获取命令的参数指引 netstat /? 0-2) 关于两个斜杠: window 文件路径中使用反斜杠:\ linux 文件路径中使用:/ 1、开关机类指令 shutdown /s # 关机shutdown /r # 重启shutdown /l …...

lintcode 1815 · 警报器 【simple vip 前缀和数组】
题目 https://www.lintcode.com/problem/1815 一个烟雾警报器会监测len秒内的烟雾值,如果这段时间烟雾值平均值大于k那么警报器会报警。现在给你n个数代表刚开始工作n秒内警报器监测的烟雾值(警报器从第len秒开始判断是否报警),…...
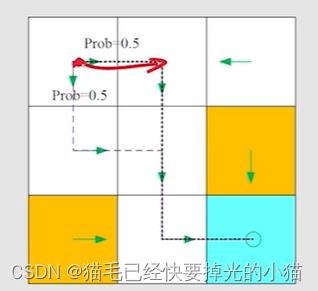
【强化学习】MDP马尔科夫链
基本元素 状态集:表示智能体所处所有状态的全部可能性的集合。类似的集合,行为集,回报集决策:规定我在某个状态下,我做出某个action马尔可夫链:学术上来说是无记忆性质。说白了就是我只在乎我目前的状态。…...

SpringBoot自写项目记录
设置静态资源映射 Slf4j 用来打印日志 Configuration Slf4j //设置静态资源映射 public class WebMvcConfig extends WebMvcConfigurationSupport {Overrideprotected void addResourceHandlers(ResourceHandlerRegistry registry) {log.info("开始静态资源配置");r…...
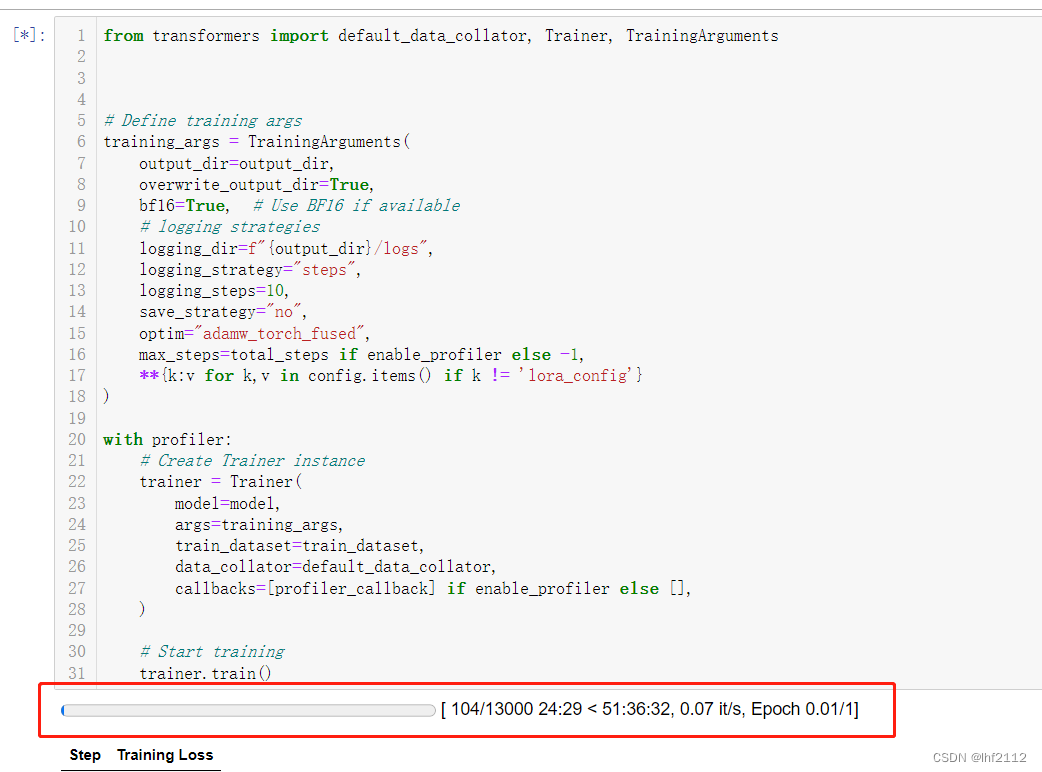
Windows10上使用llama-recipes(LoRA)来对llama-2-7b做fine-tune
刚刚在Windows10上搭建环境来对llama2做finetune,里面坑还是挺多的,这里把印象中的坑整理了一下以作备忘。 llama-recipes是meta的开源项目,Github地址为:GitHub - facebookresearch/llama-recipes: Examples and recipes for Ll…...
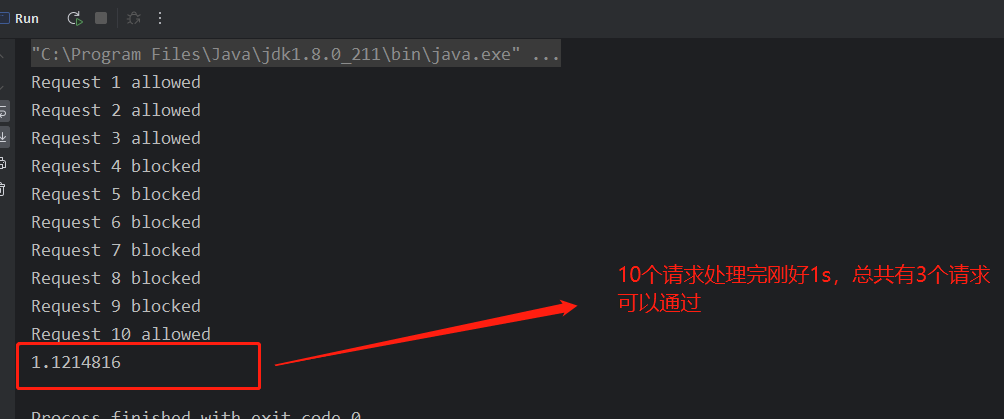
06-限流策略有哪些,滑动窗口算法和令牌桶区别,使用场景?【Java面试题总结】
限流策略有哪些,滑动窗口算法和令牌桶区别,使用场景? 常见的限流算法有固定窗口、滑动窗口、漏桶、令牌桶等。 6.1 固定窗口 概念:固定窗口(又称计算器限流),对一段固定时间窗口内的请求进行…...

2021年06月 C/C++(六级)真题解析#中国电子学会#全国青少年软件编程等级考试
C/C++编程(1~8级)全部真题・点这里 第1题:逆波兰表达式 逆波兰表达式是一种把运算符前置的算术表达式,例如普通的表达式2 + 3的逆波兰表示法为+ 2 3。逆波兰表达式的优点是运算符之间不必有优先级关系,也不必用括号改变运算次序,例如(2 + 3) * 4的逆波兰表示法为* + 2 3 …...

Tuxera NTFS for Mac2023苹果电脑Mac硬盘读写工具
Tuxera NTFS for Mac是一款高效稳定的NTFS读写工具,可以让你在Mac上完整地读写兼容NTFS格式驱动器,对磁盘进行访问、编辑、存储和传输文件等操作。Tuxera NTFS for Mac软件是一款高效稳定的NTFS读写工具,可以让你在Mac上完整地读写兼容NTFS格…...
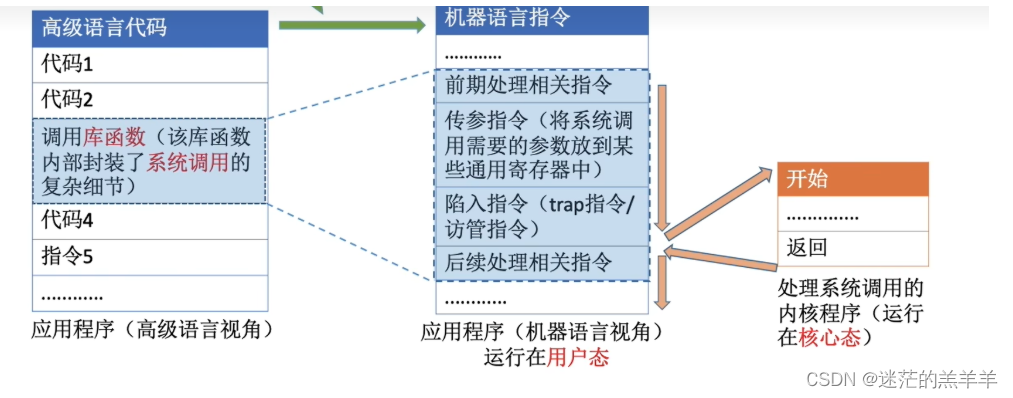
系统调用的过程
系统调用也是库函数的底层实现,当高级语言代码中如调用了库函数,在编译为机器语言指令后,指令包含前期处理相关命令、传参指令、陷入指令、后续处理相关指令。在执行陷入指令时发生内中断,使CPU进入核心态,执行对系统调…...
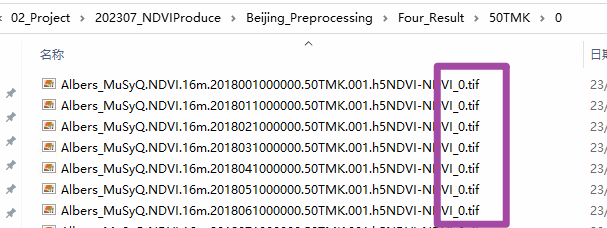
Python将多个文件的名称或后缀名由大写字母修改为小写的方法
本文介绍基于Python语言,基于一个大文件夹,遍历其中的多个子文件夹,并对于每一个子文件夹中的大量文件,批量将其文件的名称或后缀名中的字母由大写修改为小写的方法。 本文期望实现的需求为:现有一个大文件夹ÿ…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...
