洛谷——前缀和与差分
前缀和与差分
文章目录
- 前缀和与差分
- 应用总结
- 前缀和
- 截断数组
- 思路
- 代码
- 最大加权矩形
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 提示
- 思路
- 代码
- 差分
- 海底高铁
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 提示
- 思路
- 代码
- 改变数组元素
- 思路
- 代码
应用总结
-
前缀和用来查询一段区间的和。
具体应用有求最大子段和,求二维矩阵规定长度的子矩阵和,对于没有规定具体长度的子矩阵和可以通过前缀和压缩 -
差分
对一段区间的操作,转换为对首尾差值的加减。
应用于对一段区间整体操作,与前缀和相结合输出结果。
前缀和
截断数组
给定一个长度为 n
的数组 a1,a2,…,an
。
现在,要将该数组从中间截断,得到三个非空子数组。
要求,三个子数组内各元素之和都相等。
请问,共有多少种不同的截断方法?
输入格式
第一行包含整数 n
。
第二行包含 n
个整数 a1,a2,…,an
。
输出格式
输出一个整数,表示截断方法数量。
数据范围
前六个测试点满足 1≤n≤10
。
所有测试点满足 1≤n≤105
,−10000≤ai≤10000
。
输入样例1:
4
1 2 3 3
输出样例1:
1
输入样例2:
5
1 2 3 4 5
输出样例2:
0
输入样例3:
2
0 0
输出样例3:
0
思路
将数组分为等和的三段,对应于前缀和就是,找到公差设为aveaveave为总和三分之一的前缀和数组等差数列。
公差相等,三段前缀和的特征为第一段为aveaveave,第二段为2ave2ave2ave,第三段为3ave3ave3ave。记录所有可能第一段的个数,当遍历到可能第二段时,用第一段数量更新数量,因为第一段和第二段确定后,第三段也相应确定,所以第三段可以不管他。
代码
N = 100010a = [0] * N
n = int(input())a[1 : n + 1] = list(map(int, input().split()))for i in range(1, n + 1) : # 计算前缀和a[i] += a[i - 1]if a[n] % 3 or n < 3 : # 当元素个数小于3或者和不是3的倍数时肯定无法分组print(0)
else :ave = a[n] // 3 # 公差ans, cnt = 0, 0for i in range(2, n) :if a[i - 1] == ave : cnt += 1 # 记录第一段个数if a[i] == 2 * ave : ans += cnt # 遇见每个第二段时,都能确定分段方法print(ans)
最大加权矩形
题目描述
为了更好的备战 NOIP2013,电脑组的几个女孩子 LYQ,ZSC,ZHQ 认为,我们不光需要机房,我们还需要运动,于是就决定找校长申请一块电脑组的课余运动场地,听说她们都是电脑组的高手,校长没有马上答应他们,而是先给她们出了一道数学题,并且告诉她们:你们能获得的运动场地的面积就是你们能找到的这个最大的数字。
校长先给他们一个 n×nn\times nn×n 矩阵。要求矩阵中最大加权矩形,即矩阵的每一个元素都有一权值,权值定义在整数集上。从中找一矩形,矩形大小无限制,是其中包含的所有元素的和最大 。矩阵的每个元素属于 [−127,127][-127,127][−127,127] ,例如
0 –2 –7 0 9 2 –6 2
-4 1 –4 1
-1 8 0 –2
在左下角:
9 2
-4 1
-1 8
和为 151515。
几个女孩子有点犯难了,于是就找到了电脑组精打细算的 HZH,TZY 小朋友帮忙计算,但是遗憾的是他们的答案都不一样,涉及土地的事情我们可不能含糊,你能帮忙计算出校长所给的矩形中加权和最大的矩形吗?
输入格式
第一行:nnn,接下来是 nnn 行 nnn 列的矩阵。
输出格式
最大矩形(子矩阵)的和。
样例 #1
样例输入 #1
4
0 -2 -7 09 2 -6 2
-4 1 -4 1
-1 8 0 -2
样例输出 #1
15
提示
1≤n≤1201 \leq n\le 1201≤n≤120
思路
求最大子矩阵和,让人想到了最大子段和,然而矩阵是在二维进行操作。因此需要将矩阵进行压缩,我们选择对行进行压缩,对连续的行之间可以看成是一行,通过组合的形式可以考虑到所有情况。组合通过前缀和来进行实现。
代码
N = 130
a = [[0] * N for _ in range(N)]n = int(input())for i in range(1, n + 1) :a[i][1 : n + 1] = list(map(int, input().split()))# 计算二维前缀和
for i in range(1, n + 1) :for j in range(1, n + 1) :a[i][j] += a[i - 1][j] + a[i][j - 1] -a[i - 1][j - 1]
# 进行矩阵压缩和求最大子段和
ans = -1000010
for i in range(1, n + 1) :for j in range(1, i + 1) : # 从包含1行到包含i行f = [0] * (n + 1)minn = 0for k in range(1, n + 1) :f[k] = a[i][k] - a[i - j][k]ans = max(ans, f[k] - minn)minn = min(minn, f[k])
print(ans)
差分
海底高铁
题目描述
该铁路经过 NNN 个城市,每个城市都有一个站。不过,由于各个城市之间不能协调好,于是乘车每经过两个相邻的城市之间(方向不限),必须单独购买这一小段的车票。第 iii 段铁路连接了城市 iii 和城市 i+1(1≤i<N)i+1(1\leq i<N)i+1(1≤i<N)。如果搭乘的比较远,需要购买多张车票。第 iii 段铁路购买纸质单程票需要 AiA_iAi 博艾元。
虽然一些事情没有协调好,各段铁路公司也为了方便乘客,推出了 IC 卡。对于第 iii 段铁路,需要花 CiC_iCi 博艾元的工本费购买一张 IC 卡,然后乘坐这段铁路一次就只要扣 Bi(Bi<Ai)B_i(B_i<A_i)Bi(Bi<Ai) 元。IC 卡可以提前购买,有钱就可以从网上买得到,而不需要亲自去对应的城市购买。工本费不能退,也不能购买车票。每张卡都可以充值任意数额。对于第 iii 段铁路的 IC 卡,无法乘坐别的铁路的车。
Uim 现在需要出差,要去 MMM 个城市,从城市 P1P_1P1 出发分别按照 P1,P2,P3,⋯,PMP_1,P_2,P_3,\cdots,P_MP1,P2,P3,⋯,PM 的顺序访问各个城市,可能会多次访问一个城市,且相邻访问的城市位置不一定相邻,而且不会是同一个城市。
现在他希望知道,出差结束后,至少会花掉多少的钱,包括购买纸质车票、买卡和充值的总费用。
输入格式
第一行两个整数,N,MN,MN,M。
接下来一行,MMM 个数字,表示 PiP_iPi。
接下来 N−1N-1N−1 行,表示第 iii 段铁路的 Ai,Bi,CiA_i,B_i,C_iAi,Bi,Ci。
输出格式
一个整数,表示最少花费
样例 #1
样例输入 #1
9 10
3 1 4 1 5 9 2 6 5 3
200 100 50
300 299 100
500 200 500
345 234 123
100 50 100
600 100 1
450 400 80
2 1 10
样例输出 #1
6394
提示
222 到 333 以及 888 到 999 买票,其余买卡。
对于 30%30\%30% 数据 M=2M=2M=2。
对于另外 30%30\%30% 数据 N≤1000,M≤1000N\leq1000,M\leq1000N≤1000,M≤1000。
对于 100%100\%100% 的数据 M,N≤105,Ai,Bi,Ci≤105M,N\leq 10^5,A_i,B_i,C_i\le10^5M,N≤105,Ai,Bi,Ci≤105。
思路
由于每个城市只有一段路可以到达,而每段路都需要买相应的车票或者使用IC卡。每段路互不相干,这样对于费用的计算只需要知道每一段路经过次数。由于出差每次访问城市可能不是相邻的,所以对于每次的访问需要改变所有途经的路径,这就可以使用差分来记录了。
代码
N = 100010
a = [0] * N
f = [0] * N
n, m = map(int, input().split())a[1 : m + 1] = list(map(int, input().split()))# 计算差分,路径按照小的城市号规定
for i in range(2, m + 1) :x, y = a[i - 1], a[i]f[min(x, y)] += 1f[max(x, y)] -= 1
# 计算前缀和
for i in range(1, n) :f[i] += f[i - 1]
res = 0
for i in range(1, n) :x, y, z = map(int, input().split())res += min(x * f[i], z + y * f[i])
print(res)
改变数组元素
给定一个空数组 V
和一个整数数组 a1,a2,…,an
。
现在要对数组 V
进行 n
次操作。
第 i
次操作的具体流程如下:
从数组 V
尾部插入整数 0
。
将位于数组 V
末尾的 ai
个元素都变为 1
(已经是 1
的不予理会)。
注意:
ai
可能为 0
,即不做任何改变。
ai
可能大于目前数组 V
所包含的元素个数,此时视为将数组内所有元素变为 1
。
请你输出所有操作完成后的数组 V
。
输入格式
第一行包含整数 T
,表示共有 T
组测试数据。
每组数据第一行包含整数 n
。
第二行包含 n
个整数 a1,a2,…,an
。
输出格式
每组数据输出一行结果,表示所有操作完成后的数组 V
,数组内元素之间用空格隔开。
数据范围
1≤T≤20000
,
1≤n≤2×105
,
0≤ai≤n
,
保证一个测试点内所有 n
的和不超过 2×105
。
输入样例:
3
6
0 3 0 0 1 3
10
0 0 0 1 0 5 0 0 0 2
3
0 0 0
输出样例:
1 1 0 1 1 1
0 1 1 1 1 1 0 0 1 1
0 0 0
思路
每次操作都是将一段区间进行操作,很显然用差分的做法。在进行前缀和后只需要判断是否为0,即可判断是否被操作过。
代码
'''
0代表未操作
其他数字ai代表将本位置起的ai个元素全部变为1
差分是对一段区间进行一次性操作,我们只需要统一区间操作的情况下,
进行操作(比如如果有操作则统一+1),那么只要差分后的前缀和不是0则证明被变为1过
'''T = int(input())for _ in range(T) :n = int(input())a = [0] * (n + 2)f = [0] * (n + 2)f[1 : n + 1] = list(map(int, input().split()))for i in range(1, n + 1) :if f[i] :if f[i] >= i :a[1] += 1else :a[i - f[i] + 1] += 1a[i + 1] -= 1for i in range(1, n + 1) :a[i] += a[i - 1]if a[i] != 0 :print(1, end = " ")else : print(0, end = " ")print()相关文章:

洛谷——前缀和与差分
前缀和与差分 文章目录前缀和与差分应用总结前缀和截断数组思路代码最大加权矩形题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1提示思路代码差分海底高铁题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1提示思路代码改变数组元素思路代码应用总结 前缀和用来…...

离线内网环境部署更新问题记录
文章目录低级错误错误一 配置文件参数错误错误二 文件位置错误新遇到的错误其他遇到的问题经验教训低级错误 错误一 配置文件参数错误 在与现场实施人员沟通时,出现信息错位,实施人员发来的截图里的ip地址不是正在使用的ip地址(机器c重装系…...

【Git】Git是什么?简单说说Git的工作机制?Git的常用命令有那些?
目录 一、Git是什么? 二、简单说说Git的工作机制? 三、Git的常用命令有那些? 💟 创作不易,不妨点赞💚评论❤️收藏💙一下 一、Git是什么? Git 是一个免费的、开源的分布式版本控制系统,可…...

《精通Spring4.x 企业应用开发实战》第1章 Spring概述
目录标题前言一、Spring带给我们什么二、Spring体系结构三、Spring4.0新特性核心容器的增强泛型依赖注入Map依赖注入Lazy延迟依赖注入List注入Conditional 注解CGLIB 代理类增强其他四、Spring 子项目总结前言 汇总:《精通Spring4.x 企业应用开发实战》 一、Spring带…...

【Spring Cloud Alibaba】003-Nacos 概述与单机搭建
【Spring Cloud Alibaba】003-Nacos 概述与单机搭建 文章目录【Spring Cloud Alibaba】003-Nacos 概述与单机搭建一、Nacos 概述0、新技术学习思路推荐1、什么是 Nacos2、架构图架构图架构图信息二、Nacos 单机搭建1、下载与启动下载地址编辑 startup.cmd 文件下面对两种模式的…...
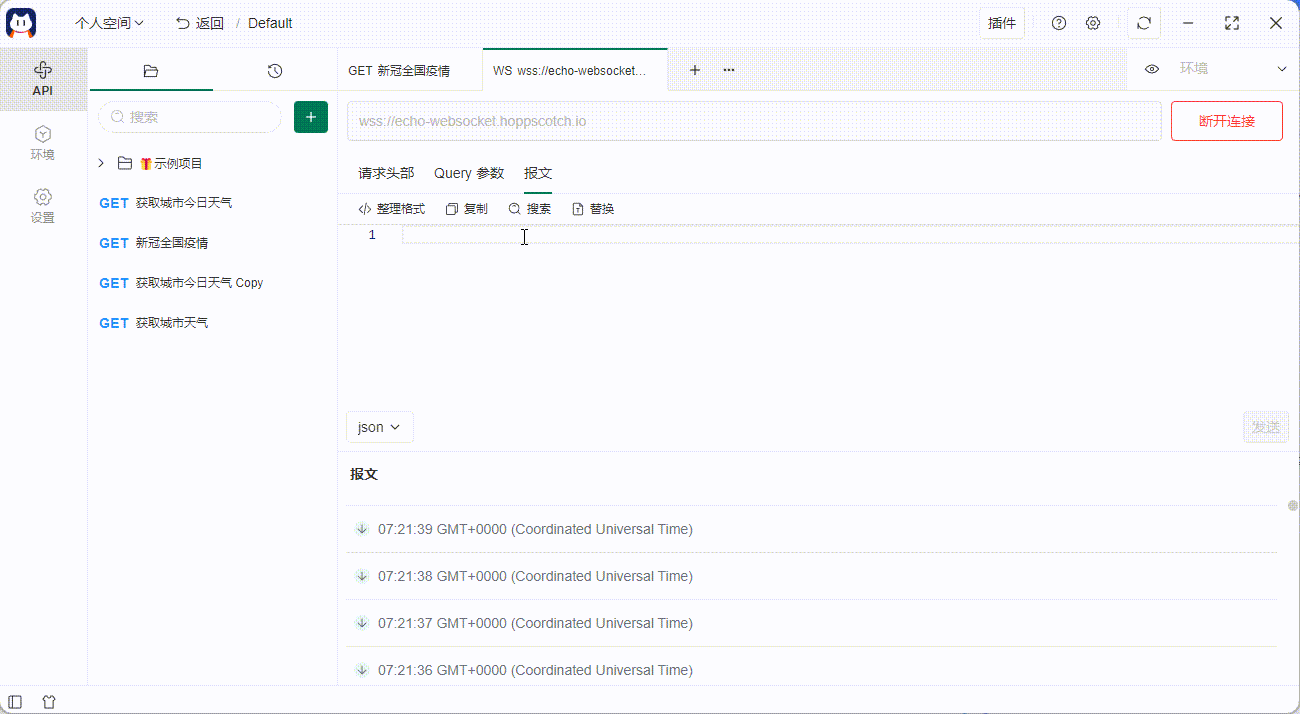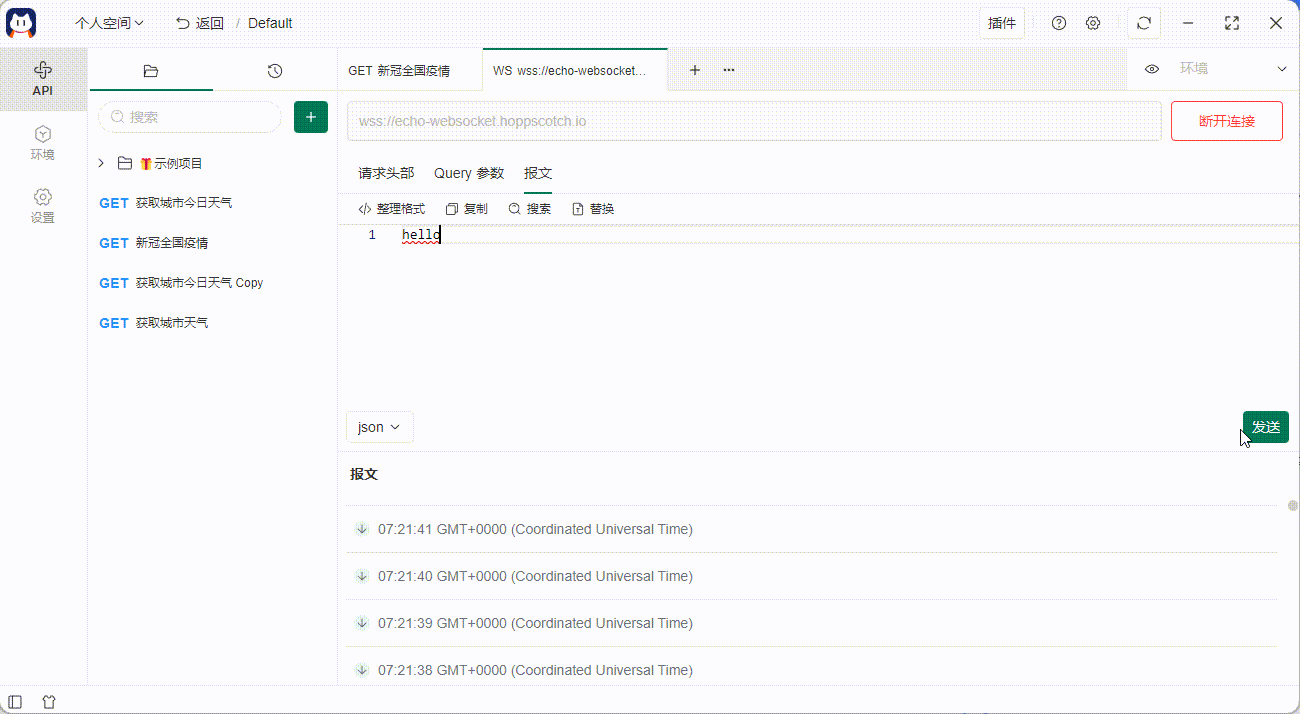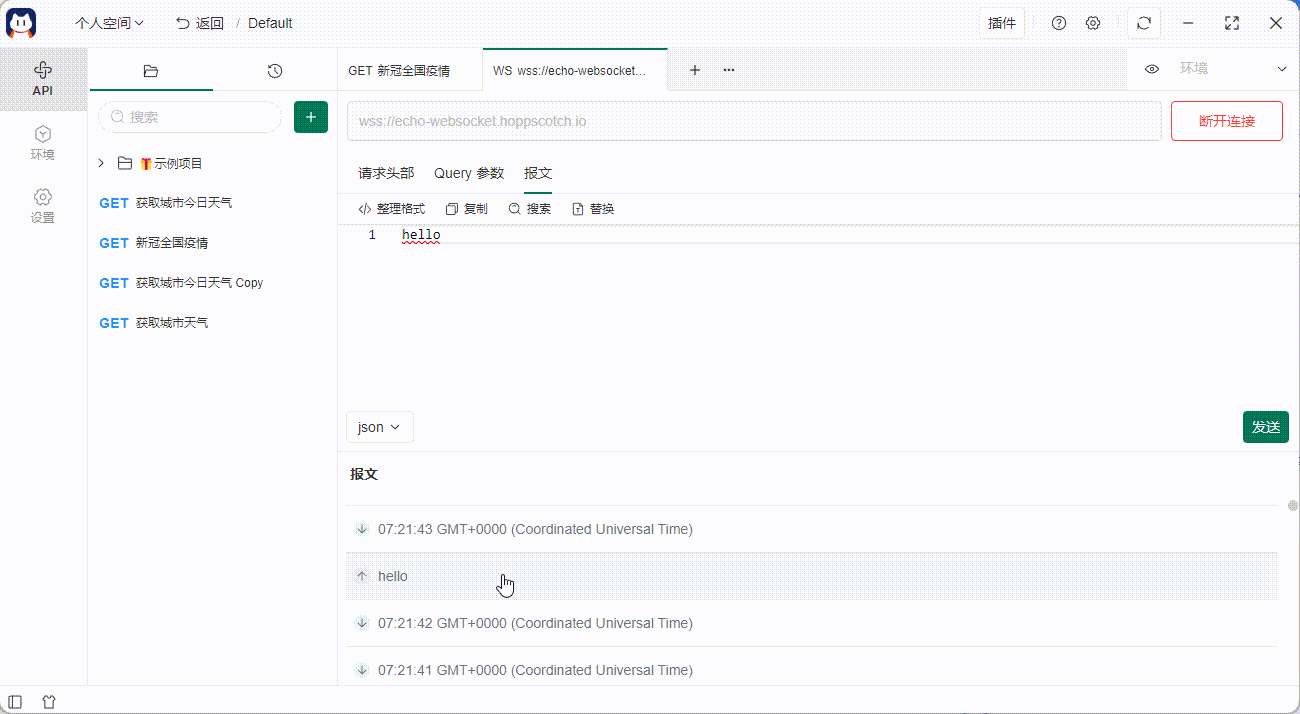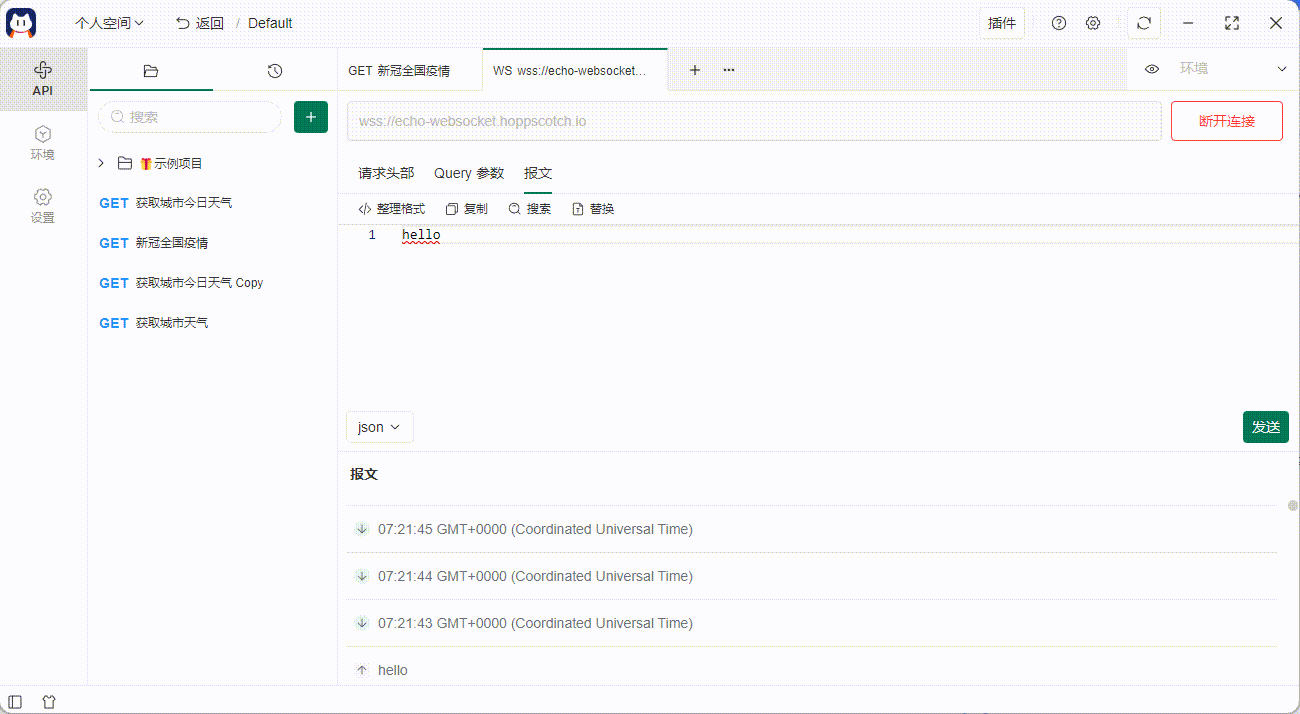
如何使用 API 工具做 Websocket 测试
在 API 测试中,对 Websocket 协议的支持呼声越来越高,今天给大家推荐一款 开源的 API 管理工具——Postcat,以及教教大家,如何利用 API 管理工具做 Websocket 测试。 在线 Demo 链接:Postcat - Open Source API Ecosys…...

90%的人都理解错了HTTP中GET与POST的区别
Get和Post是HTTP请求的两种基本方法,要说它们的区别,接触过WEB开发的人都能说出一二。 最直观的区别就是Get把参数包含在URL中,Post通过request body传递参数。 你可能自己写过无数个Get和Post请求,或者已经看过很多权威网站总结…...

【C++】秋招实习面经汇总篇
C面经汇总 系列综述: 目的:本系列是个人整理为了秋招和实习面试的,整理期间苛求每个知识点,平衡背诵量与深入程度。 来源:材料主要源于阿秀的笔记和《王道考研复习指导》进行的,每个知识点的修正和深入主要…...

干货分享:2023欧美市场分析与机会
1、2023年欧美市场分析美国是⼀个消费大国,正常情况下做外贸不可忽略的市场。如何找客户:专注产业链 。产业链对接,其上游是什么,那么他就是我的客户 ( 原材料-⼯⼚)南美洲是北美的经济殖民地(矿产资源农产品),非洲仍然…...
介绍Kadence Elements元素模板:按您的方式设计网站
随着 Kadence Pro 1.0.4 和 Kadence Blocks Pro 1.5.8 的发布,Kadence 团队很高兴地宣布推出最强大的新方法,帮助网站所有者使用 Kadence Elements Templates 创建动态和高度定制的 WordPress 网站。如果您曾经创建过 WordPress 网站,并且发现…...
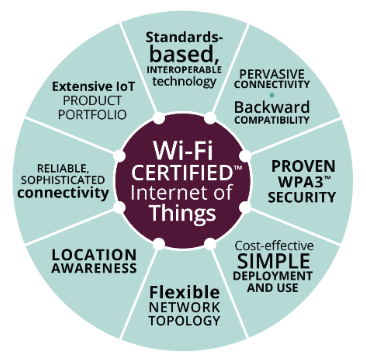
物联网发展的重要通信技术Wi-Fi
Wi-Fi 可以适应各种场景的联网需求 Wi-Fi 在实现物联网创新方面发挥了基础性作用,提供了广泛的连接性,将各种“事物”相互连接、连接到互联网,以及连接到全球使用的 180 亿台 Wi-Fi 设备。物联网的经济潜力是无限的,Wi-Fi 为智能…...
OSS上传(Java和Js)
OSS上传(Java和Js)准备工作创建RAM用户创建角色创建权限策略给角色授予权限策略获取临时访问凭证Java普通上传OSSJava分片上传OSSJS普通上传OSSJS分片上传OSS使用RAM用户或STS方式访问 由于阿里云账号AccessKey拥有所有API访问权限,建议遵循阿…...
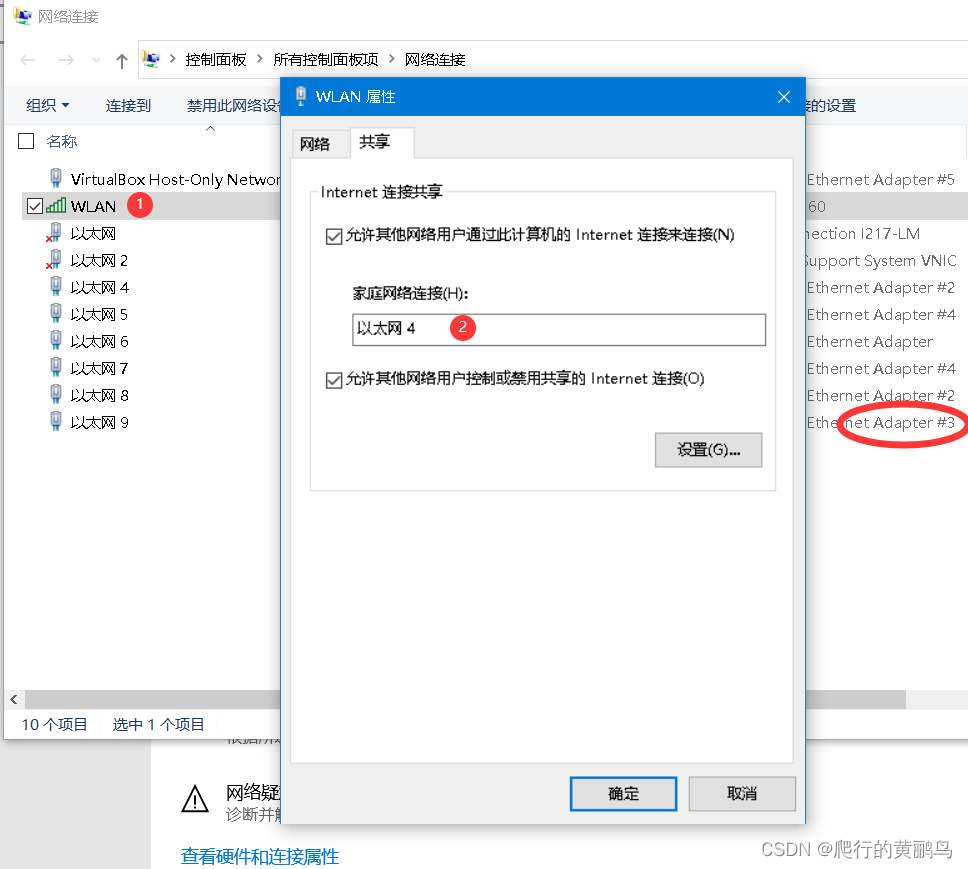
【虚拟机】VirtualBox Host-Only + 主机网络共享配置
文章目录创建Host-Only虚拟机配置主机配置其它工作中经常会使用到虚拟机进行各种技术的试验,之前为了省事常用桥接模式,可是我经常变换办公地点,每个办公地点的局域网网段并不一样,所以我采取了仅主机模式网络共享这种方式&#x…...

小公司“混”的3年,我认真做了5件事,真的受益终生
小公司“混”的3年,我认真做了5件事,真的受益终生 目录:导读 功能测试很重要但不值钱 自动化测试在小公司没市场,但是你得会 给自己的一些忠告 第一件事:分清阶段,制定计划 第二件事:梳理…...
Linux Crontab命令定时任务基本语法与操作教程
Linux Crontab命令定时任务基本语法与操作教程 一、Crontab查看编辑重启 1、查看crontab定时执行任务列表 crontab -l 2、编辑crontab定时执行任务 crontab -e 3、删除crontab定时任务 crontab -r 4、相关命令: sudo service crond start #启动服务 sudo …...

文档测试要测什么,如何进行测试?
文档测试要测什么,如何进行测试? 对于交付用户文档来说,以需求、用户手册、安装手册等为主,检查用户文档是否和实际的存在差别,主要从以下几个方面来考虑: 阅读者:文档面向的读者定位要清晰&…...

.net 6 引入EFCore
这里默认使用sql server数据库 DBFirst nuget引入程序集 Microsoft.EntityFrameworkCore Microsoft.EntityFrameworkCore.SqlServer Microsoft.EntityFrameworkCore.Design Microsoft.EntityFrameworkCore.Tools Microsoft.Extensions.Logging.Console 执行脚本 设置DAL…...

MySQL------自定义排序
1、MySQL函数 field() 实现自定义 语法: SELECT * from table_name ORDER BY FIELD(str,str1,str2,str3,…) str: 字段名, str1,str2,str3: 自定义排序的数值 例1排序-所有值: 先姓名排序后出生日期排序 SELECT * from name_info ORDER BY FIELD(name…...
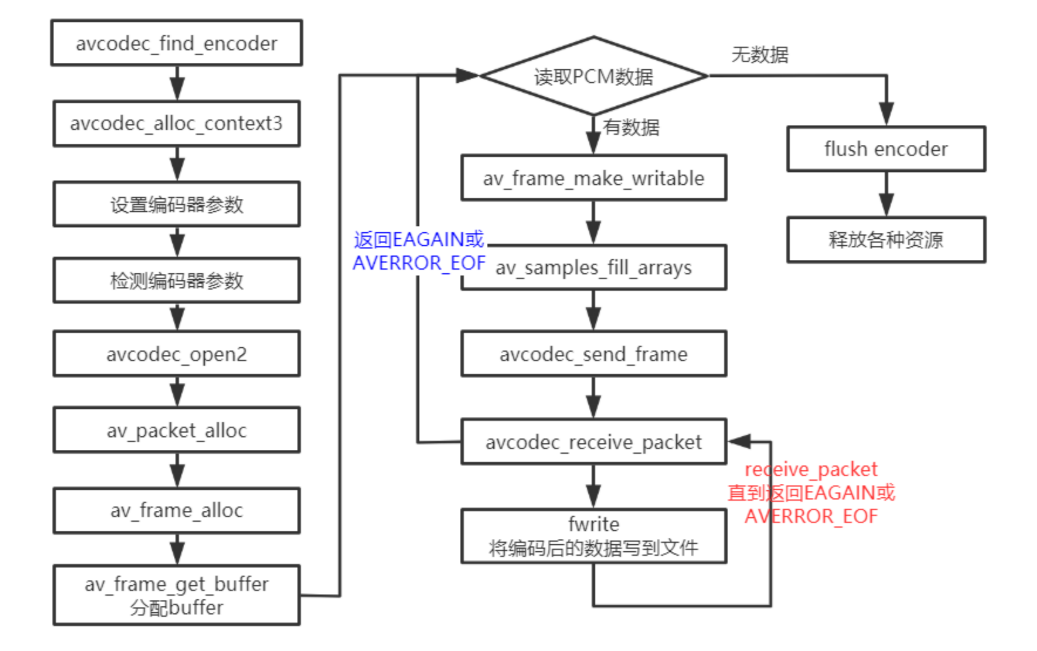
FFMPEG自学二 ⾳频编码实战
一、FFmpeg编码流程二、流程关键函数avcodec_find_encoder:根据指定的AVCodecID查找注册的编码器。 avcodec_alloc_context3:为AVCodecContext分配内存。 avcodec_open2:打开编码器。 avcodec_send_frame:将AVFrame⾮压缩数据给…...

一致魔芋在北交所上市:市值突破11亿元,吴平夫妇为实控人
2月21日,湖北一致魔芋生物科技股份有限公司(下称“一致魔芋”,BJ:839273)在北京证券交易所上市。本次上市,一致魔芋的发行价为11.38元/股,发行1350万股,募资总额约为1.54亿元。 本次发行后&…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...
