2023.9.3 关于 AVL 树
目录
二叉搜索树
二叉搜索树的简介:
二叉搜索树的查找:
二叉搜索树的效率:
AVL树
AVL 树的简介:
AVL 树的实现:
AVL树的旋转
右单旋
左单旋
左右双旋
右左双旋
完整 AVL树插入代码
验证 AVL 树
AVL 树的性能
二叉搜索树
- 要想了解关于二叉平衡树的相关知识,了解二叉搜索树的相关概念是其前提!
二叉搜索树的简介:
特点:
- 结点的左子树上所有节点的值都小于该结点的值
- 结点的右子树上所有结点的值都大于该结点的值
- 左右子树也都是二叉搜索树
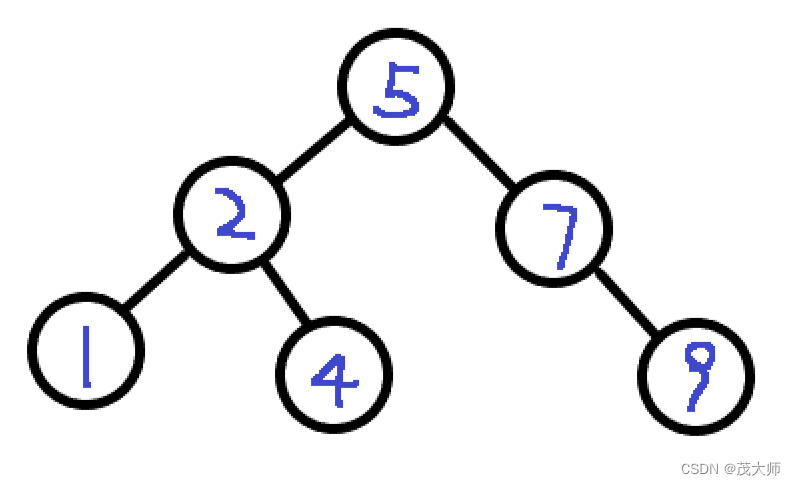
例图如下:
特性:
- 二叉搜索树最左侧节点为最小的节点,最右侧节点为最大的节点
- 采用中序遍历遍历二叉搜索树,能得到一个有序的序列
二叉搜索树的查找:
- 当根节点为空时,则返回 false
- 当根节点的值等于查询值,则返回 ture
- 当根节点的值小于查询值,则向其左子树进行查找
- 当根节点的值大于查询值,则向其右子树进行查找
例图如下:
当我们要查询 9 时,其二叉搜索树的查询过程如下:
先由根节点 5 开始,比较其值与查询值,发现 5 < 9 进而查询其右子树
到其右子树根节点,比较其值与查询值,发现 7 < 9 进而查询其右子树
到其右子树根节点,比较其值与查询值,发现 9 = 9,查询完毕 返回 ture
二叉搜索树的效率:
- 二叉搜索树的平均查找长度与其节点的深度有关,节点越深,则比较次数越多!
上文例图中我们对数值 9 进行查询,进行了3次比较
下面的例图:同样为6个节点,同样是对9进行查询
根据上文二叉搜索树的查找方式,我们会发现其进行了 6 次比较
显然节点的插入次序不同,得到的二叉搜索树也会不同,导致当对同样的数值进行查找时,其效率也会有较大相差
最优情况:
该二叉搜索树树为二叉完全树,平均的比较次数为:log2N
最坏情况:
该二叉搜索树树为单枝树,平均的比较次数为:N/2
AVL树
当想避免二叉搜索树最坏情况出现时,AVL 树便是优化后的二叉搜索树!
AVL 树的简介:
特点:
- 结点的左子树上所有节点的值都小于该结点的值
- 结点的右子树上所有结点的值都大于该结点的值
- 其左右子树的高度差(平衡因子)的绝对值不超过 1
- 左右子树也都是 AVL 树
例图如下:
优点:
- 可以有效的降低树的高度,不会出现像单枝树这样的极端情况,有效的减少平均查找次数
AVL 树的实现:
1. 定义 AVL 树:
- 首先我们创建一个 TreeNode 静态类,将 AVL 树的相关属性定义完成
public class AVLTree {static class TreeNode {public int val;public int bf;//平衡因子 这里的平衡因子我们是 右子树高度-左子树高度public TreeNode left;//左孩子的引用public TreeNode right;//右孩子的引用 public TreeNode parent;//父亲节点的引用 // 构造方法public TreeNode(int val) {this.val=val;}}public TreeNode root;//根节点 }2. 插入新结点:
- 第一步:先按照二叉搜索树插入结点方式进行新结点的插入
public boolean insert(int val) { // 根据传来的参数,创建一个新结点TreeNode node = new TreeNode(val); // 判断根结点是否为空,为空则代表 AVL 树为空,直接将新插入的结点作为根结点即可if(root == null ){root = node;return true;} // 创建一个 cur 结点,利用该结点去遍历这个树的结点TreeNode cur = root;//创建一个 parent 结点,该结点记录 cur 的父亲结点TreeNode parent = null; // 创建该循环的目的是为了根据新增结点的值,来找到属于它应该插入的位置,当 cur == null 时,退出循环 且 parent 为新插入结点的父亲结点while (cur != null){if(cur.val > val) { // 如果 cur 所指向的结点的值大于新增加结点的值,则向左寻找parent = cur;cur = cur.left;}else if (cur.val == val) { // 新插入结点的值与 cur 所指向的结点的值相等,表示 AVL 树已有一个值与之相等的结点,因为 AVL 树中每个结点的值必须是唯一的,从而不必再插入一个重复值的结点return false;}else { // 如果 cur 所指向的节点的值小于新增加结点的值,则向右寻找parent = cur;cur = cur.right;}} // 走到这说明 cur == null,意思是已经找到了新结点需要插入的位置,且 parent 结点已经记录到了 新结点的父亲结点 的位置if (parent.val > val){parent.left = node;}else {parent.right = node;}return true;}
- 第二步:根据插入结点后平衡因子的变化,对该树进行相应的调整,维持平衡因子的绝对值为 1
情况一:parent 结点平衡因子的绝对值为 0,该树无需调整
情况二:parent 结点平衡因子的绝对值为 1,该树不一定平衡,需向上继续查看结点,检查其平衡因子的绝对值
情况三:parent 结点平衡因子的绝对值为 2,该树一定不平衡,根据实际情况,对该树进行相应调整
- 结合上述三种情况我们可以先写出代码的大致框架,至于如何对树进行调整则有好几种情况
public boolean insert(int val) {TreeNode node = new TreeNode(val);if(root == null ){root = node;return true;}TreeNode cur = root;TreeNode parent = null;while (cur != null){if(cur.val > val) {parent = cur;cur = cur.left;}else if (cur.val == val) {return false;}else {parent = cur;cur = cur.right;}}if (parent.val > val){parent.left = node;}else {parent.right = node;}// 这里定义一下新结点的父亲结点为 parentnode.parent = parent; // 因为上段代码 cur == null,所以指定一下 cur 指向 node 结点,好为后面平衡因子的调整做准备cur = node;// 根据平衡因子进行树的调整 // 当 parent == null 时,说明 parent 已经爬到该树的根节点之上了,也就是调整完该树了while (parent != null) {if (cur == parent.right) { // 新增结点在右树parent.bf++;}else { // 新增结点在左树parent.bf--;} // 在这里检查 parent 结点平衡因子绝对值的值if(parent.bf == 0) { // 这里说明已经平衡了,无需调整}else if(parent.bf == 1 || parent.bf == -1) { // 虽然 parent 结点是平衡的,但是还需向上查看结点,因为有可能不平cur = parent;parent = cur.parent;}else { // 这里说明 parent 的平衡因子的绝对值为 2 了,该树必不平衡if (parent.bf == 2) {if (cur.bf == 1) {}else { // 这里是 cur.bf == -1}}else { // 这里是 parent.bf == -2if (cur.bf == -1) {}else { // 这里是 cur.bf == 1}}} } return true;}
AVL树的旋转
右单旋
具体解析:
- 5结点 为新插入结点
代码:
看图理解代码相应含义
private void rotateRight(TreeNode parent) {TreeNode subL = parent.left;TreeNode subLR = subL.right;parent.left = subLR;subL.right = parent;subLR.parent = parent;parent.parent = subL;}
- 当然上述仅是 60结点 作为根结点的情况,还有 60结点 不为根结点的情况也许考虑到
更新代码:
private void rotateRight(TreeNode parent) {TreeNode subL = parent.left;TreeNode subLR = subL.right;parent.left = subLR;subL.right = parent;subLR.parent = parent; // 这里必须先记录下 parent 的父亲结点TreeNode pParent = parent.parent;parent.parent = subL; // 检查 parent 是否为根结点if(parent == root) {root = subL;root.parent = null;}else { // 此时parent 是都父亲节点的,从而需要判断 parent是左子树的还是右子树的if(pParent.left == parent) {pParent.left = subL;}else {pParent.right = subL;}subL.parent = pParent;}}
- 当然右单旋完树之后还需要,调节其他结点的平衡因子
更新代码:
private void rotateRight(TreeNode parent) {TreeNode subL = parent.left;TreeNode subLR = subL.right;parent.left = subLR;subL.right = parent;subLR.parent = parent; // 这里必须先记录下 parent 的父亲结点TreeNode pParent = parent.parent;parent.parent = subL; // 检查 parent 是否为根结点if(parent == root) {root = subL;root.parent = null;}else { // 此时parent 是都父亲节点的,从而需要判断 parent是左子树的还是右子树的if(pParent.left == parent) {pParent.left = subL;}else {pParent.right = subL;}subL.parent = pParent;} // 更新上图两个结点的平衡因子subL.bf = 0;parent.bf = 0;}
- 当然我们上述思路中,还有一个问题没有考虑到,就是 subLR 可能为空
最终代码:
- 此代码为完整右单旋逻辑代码
private void rotateRight(TreeNode parent) {TreeNode subL = parent.left;TreeNode subLR = subL.right;parent.left = subLR;subL.right = parent; // 如果 subLR 不为 null,我们才执行,该行代码if(subLR != null){subLR.parent = parent;} // 这里必须先记录下 parent 的父亲结点TreeNode pParent = parent.parent;parent.parent = subL; // 检查 parent 是否为根结点if(parent == root) {root = subL;root.parent = null;}else { // 此时parent 是都父亲节点的,从而需要判断 parent是左子树的还是右子树的if(pParent.left == parent) {pParent.left = subL;}else {pParent.right = subL;}subL.parent = pParent;} // 更新上图两个结点的平衡因子subL.bf = 0;parent.bf = 0;}
左单旋
- 代码上左单旋和右单旋逻辑上是一样的,可参照着右单旋代码写
最终代码:
- 此代码为完整左单旋逻辑代码
private void rotateLeft(TreeNode parent) {TreeNode subR = parent.right;TreeNode subRL = subR.left;parent.right = subRL;subR.left = parent;if(subRL != null) {subRL.parent = parent;}TreeNode pParent = parent.parent;parent.parent = subR;if (root == parent) {root = subR;root.parent = null;}else {if (pParent.left == parent){pParent.left = subR;}else {pParent.right = subR;}subR.parent = pParent;}subR.bf = 0;parent.bf = 0;}
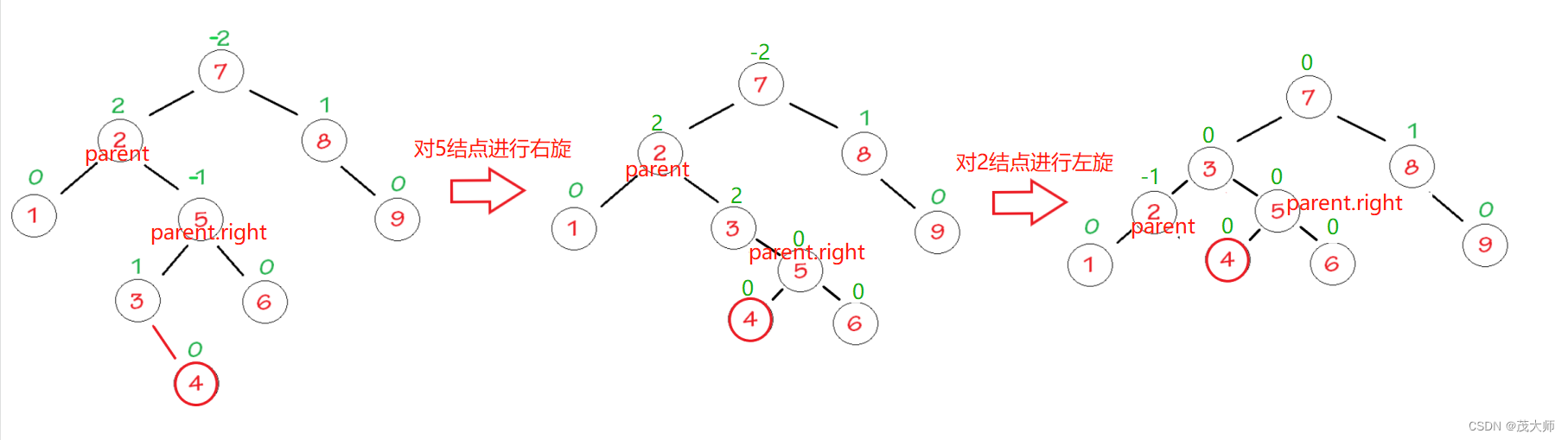
左右双旋
代码:
- 看图理解代码相应含义
private void rotateLR(TreeNode parent) { // 先左旋后右旋rortateLeft(parent.left);rortateRight(parent);}
- 当然左右双旋完树之后还需要,调节其他结点的平衡因子
最终代码:
- 此代码为完整左右双旋逻辑代码
private void rotateLR(TreeNode parent) {TreeNode subL = parent.left;TreeNode subLR = subL.right;int bf = subLR.bf; // 先左旋后右旋rotateLeft(parent.left);rotateRight(parent); // 明确一点,当 bf 为 0 时,本身就是平衡的,无需再修改平衡因子if(bf == -1){subL.bf = 0;subLR.bf = 0;parent.bf = 1;}else if(bf == 1){subL.bf = -1;subLR.bf = 0;parent.bf = 0;}}
右左双旋
最终代码:
- 此代码为完整左右双旋逻辑代码
private void rotateRL(TreeNode parent) {TreeNode subR = parent.right;TreeNode subRL = subR.left;int bf = subRL.bf;rotateRight(parent.right);rotateLeft(parent);if(bf == -1){parent.bf = -1;subR.bf = 0;subRL.bf = 0;}else if(bf == 1){parent.bf = 0;subR.bf = 1;subRL.bf = 0;}}
完整 AVL树插入代码
- 我们将这四种旋转填入到相对应的位置
public boolean insert(int val) {//根据传来的参数,创建一个新结点TreeNode node = new TreeNode(val); // 判断根结点是否为空,为空则代表 AVL 树为空,直接将新插入的结点作为根结点即可if(root == null ){root = node;return true;} // 创建一个 cur 结点,利用该结点去遍历这个树的结点TreeNode cur = root;//创建一个 parent 结点,该结点记录 cur 的父亲结点TreeNode parent = null; // 创建该循环的目的是为了根据新增结点的值,来找到属于它应该插入的位置,当 cur == null 时,退出循环 且 parent 为新插入结点的父亲结点while (cur != null){if(cur.val > val) { // 如果 cur 所指向的结点的值大于新增加结点的值,则向左寻找parent = cur;cur = cur.left;}else if (cur.val == val) { // 新插入结点的值与 cur 所指向的结点相等,表示 AVL 树已有一个值与之相等的结点,因为 AVL 树中每个结点的值必须是唯一的,从而不必再插入一个重复值的结点return false;}else { // 如果 cur 所指向的节点的值小于新增加结点的值,则向右寻找parent = cur;cur = cur.right;}} // 走到这说明 cur == null,意思是已经找到了新结点需要插入的位置,且 parent 结点已经记录到了 新结点的父亲结点 的位置if (parent.val > val){parent.left = node;}else {parent.right = node;}// 这里定义一下新结点的父亲结点为 parentnode.parent = parent; // 因为上段代码 cur == null,所以指定一下 cur 指向 node 结点,好为后面平衡因子的调整做准备cur = node;// 根据平衡因子进行树的调整 // 当 parent == null 时,说明 parent 已经爬到该树的根节点之上了,也就是调整完该树了while (parent != null) {if (cur == parent.right) { // 新增结点在右树parent.bf++;}else { // 新增结点在左树parent.bf--;} // 在这里检查 parent 结点平衡因子绝对值的值if(parent.bf == 0) { // 这里说明已经平衡了,无需调整}else if(parent.bf == 1 || parent.bf == -1) { // 虽然 parent 结点是平衡的,但是还需向上查看结点,因为有可能不平cur = parent;parent = cur.parent;}else { // 这里说明 parent 的平衡因子的绝对值为 2 了,该树必不平衡if (parent.bf == 2) {if (cur.bf == 1) { // 这里进行左旋rotateLeft(parent);}else { // 这里是 cur.bf == -1,进行右左双旋rotateRL(parent);}}else { // 这里是 parent.bf == -2if (cur.bf == -1) { // 这里进行右旋rotateRight(parent);}else { // 这里是 cur.bf == 1,进行左右双旋rotateLR(parent);}} // 注意:只要进行过一次旋转,该树便会平衡,无需继续该 while 循环break;}}return true;}
验证 AVL 树
两条性质:
- 中序遍历 AVL 树可以得到一个有序序列
- 每个结点子树高度差的绝对值不超过 1
代码:
// 验证是否平衡public boolean isBalanced(TreeNode root) {if(root == null) {return true;}int leftH = height(root.left);int rightH = height(root.right);if(rightH - leftH != root.bf) {System.out.println("结点:" + root.val + "的平衡因子异常");return false;}return Math.abs(leftH - rightH) <= 1 &&isBalanced(root.left) &&isBalanced(root.right);}// 求树的高度private int height(TreeNode root) {if(root == null) {return 0;}int leftH = height(root.left);int rightH =height(root.right);return leftH > rightH ? leftH+1 : rightH+1;}// 验证顺序public void dfs(TreeNode root) {if (root == null) {return;}dfs(root.left);System.out.println("root = " + root.val + "; ");dfs(root.right);}
AVL 树的性能
优点:
- AVL树是一颗绝对平衡的二叉搜索树,所以能够保证十分高效的查询,其时间复杂度为log2(N)
缺点:
- AVL 树不适合大量的插入和删除,因为要不断的维持AVL树的平衡,从而需要进行大量的旋转
总结:
- 需要高效查询且有序的数据结构,且该数据不会改变,可使用 AVL 树,如果该数据经常发生变化,则不适用于 AVL 树
相关文章:
2023.9.3 关于 AVL 树
目录 二叉搜索树 二叉搜索树的简介: 二叉搜索树的查找: 二叉搜索树的效率: AVL树 AVL 树的简介: AVL 树的实现: AVL树的旋转 右单旋 左单旋 左右双旋 右左双旋 完整 AVL树插入代码 验证 AVL 树 AVL 树的性…...

机器学习课后习题 --- 机器学习实践
(一)单选题 1.以下关于训练集、验证集和测试集说法不正确的是( )。 A:测试集是纯粹是用于测试模型泛化能力B:训练集是用来训练以及评估模型性能 C:验证集用于调整模型参数 D:以上说法都不对 2.当数据分布不平衡时,我们可采取的措施不包括…...

git常用操作
删除分支 例:例如想删除的分支是dev_delete,那么可以按照如下的操作进行 #查看当前所在分支 git branch#如果在当前dev_delete分支上,就要切换到其他分支才能删除该分支 git checkout 其他分支#删除本地名为dev_delete的分支 git branch -d dev_delete…...

QT的补充知识
一、文件 QFile QT提供了QFile类用于对文件进行读写操作,也提供了其他的两个类:文本流(QTextSream)和数据流(QDataStream) 文本流(QTextSream):用于对文本数据的处理&am…...
【力扣周赛】第 360 场周赛(贪心 ⭐树上倍增)
文章目录 竞赛链接Q1:8015. 距离原点最远的点(贪心)Q2:8022. 找出美丽数组的最小和(贪心)Q3:2835. 使子序列的和等于目标的最少操作次数(贪心)思路竞赛时丑陋代码&#x…...
企业如何防止数据外泄——【部署智能透明加密防泄密系统】
为防止公司文件泄密,可以采取以下措施: www.drhchina.com 分部门部署:根据不同的部门需要,为不同部门用户部署灵活的加密方案。例如,对研发部、销售部、运营部的机密资料进行强制性自动加密,对普通部门的文…...
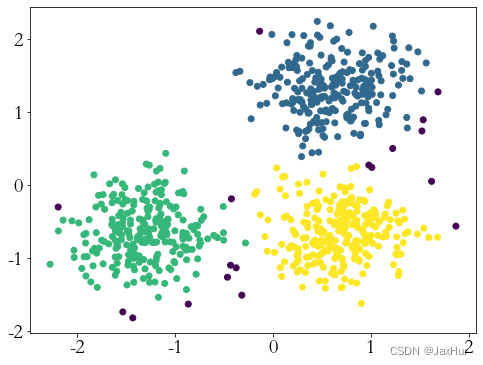
【聚类】DBCAN聚类
OPTICS是基于DBSCAN改进的一种密度聚类算法,对参数不敏感。当需要用到基于密度的聚类算法时,可以作为DBSCAN的一种替代的优化方案,以实现更优的效果。 原理 基于密度的聚类算法(1)——DBSCAN详解_dbscan聚类_root-ca…...
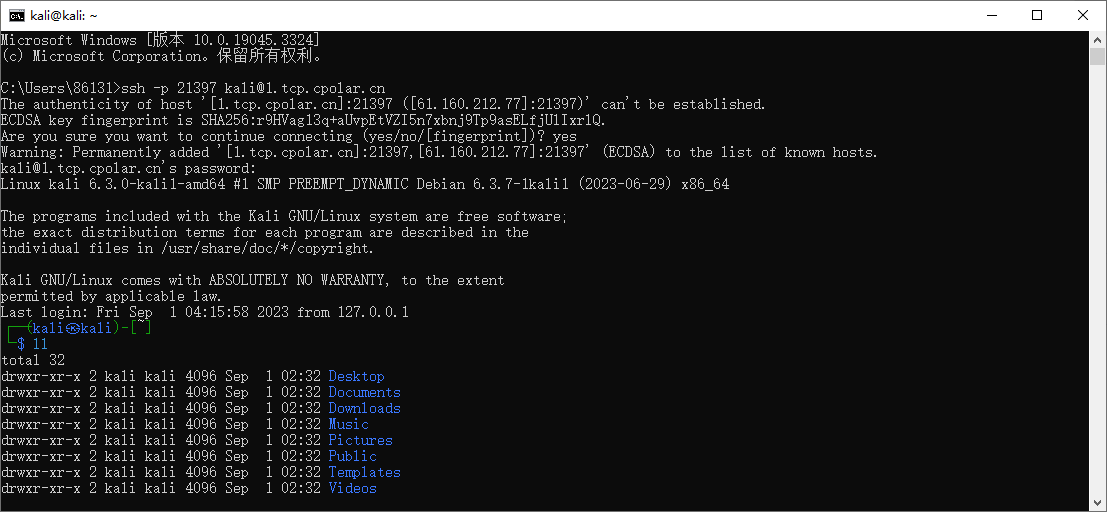
通过安装cpolar内网穿透在Kali上实现SSH远程连接的步骤指南
文章目录 1. 启动kali ssh 服务2. kali 安装cpolar 内网穿透3. 配置kali ssh公网地址4. 远程连接5. 固定连接SSH公网地址6. SSH固定地址连接测试 简单几步通过cpolar 内网穿透软件实现ssh 远程连接kali! 1. 启动kali ssh 服务 默认新安装的kali系统会关闭ssh 连接服务,我们通…...
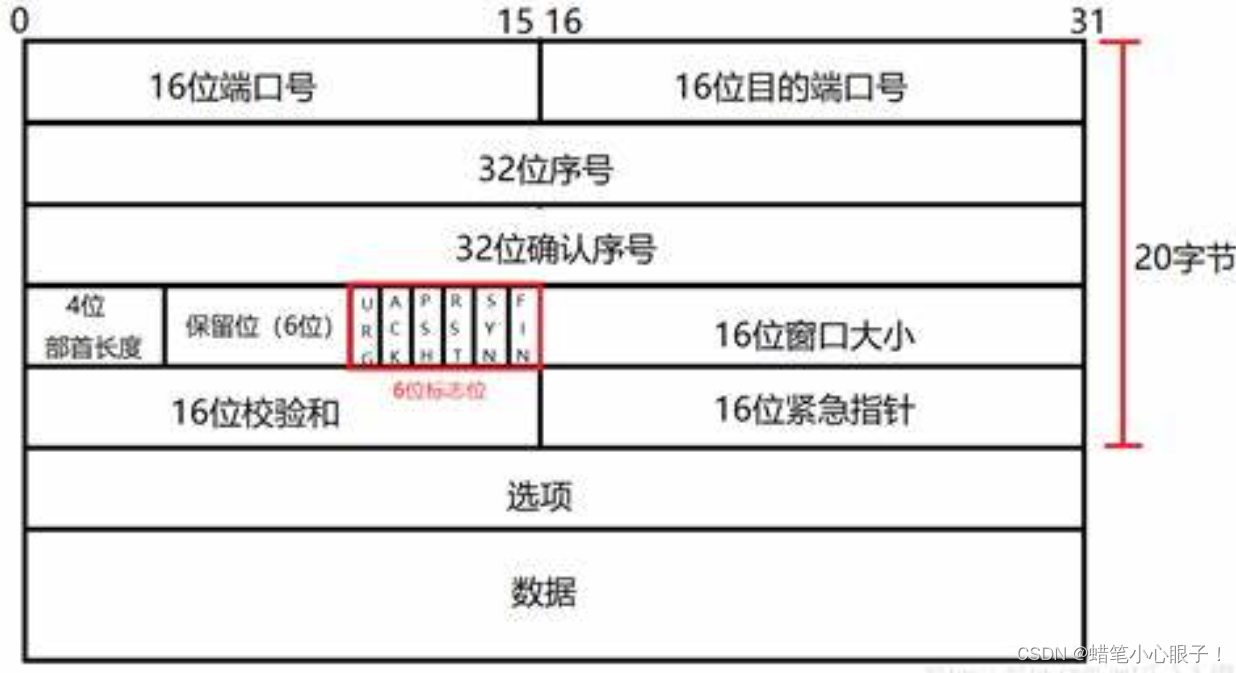
UDP和TCP协议报文格式详解
在初识网络原理(初识网络原理_蜡笔小心眼子!的博客-CSDN博客)这篇博客中,我们简单的了解了一下TCP/IP五层网络模型,这篇博客将详细的学习一下五层网络模型中传输层的两个著名协议:UDP和TCP 目录 一, 传输层的作用 二, UDP 1,UDP协议的特点 2,UDP报文格式 三, TC…...
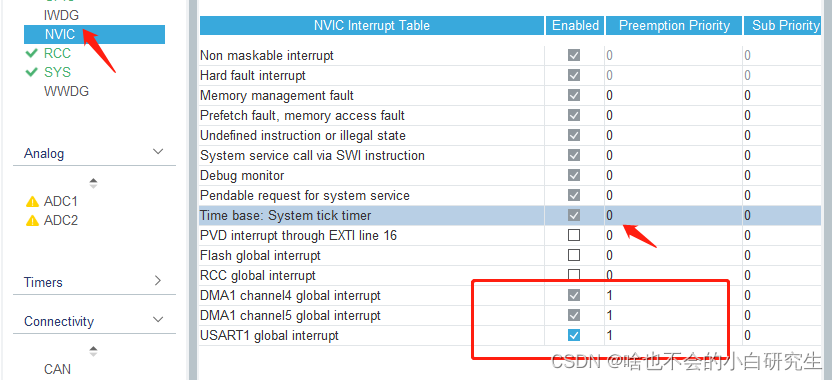
STM32+UART串口+DMA收发
目录 1、cubemax端配置 1.1 初始化配置 1.2 GPIO配置 1.3 UART配置 1.3.1 串口基础配置 1.3.2 DMA配置 2、keil端代码设计 2.1 初始化配置 2.2 DMA接收初始化配置 2.3 DMA发送配置 2.4 接收回调函数设置 2.5 回调函数内容代码编写 2.5.1 接收回调函数 2.5.2 发送回调…...

安全基础 --- js的闭包和this属性
js闭包 简介 一个函数和对其周围状态(lexical exviroment,词法环境)的引用捆绑在一起(或者说函数被引用包围),这样的组合就是闭包(closure) 在js中,通俗来讲,…...

【C语言每日一题】08. 字符三角形
题目来源:http://noi.openjudge.cn/ch0101/08 08 字符三角形 总时间限制: 1000ms 内存限制: 65536kB 问题描述 给定一个字符,用它构造一个底边长5个字符,高3个字符的等腰字符三角形。 输入 输入只有一行, 包含一个字符。 输出…...
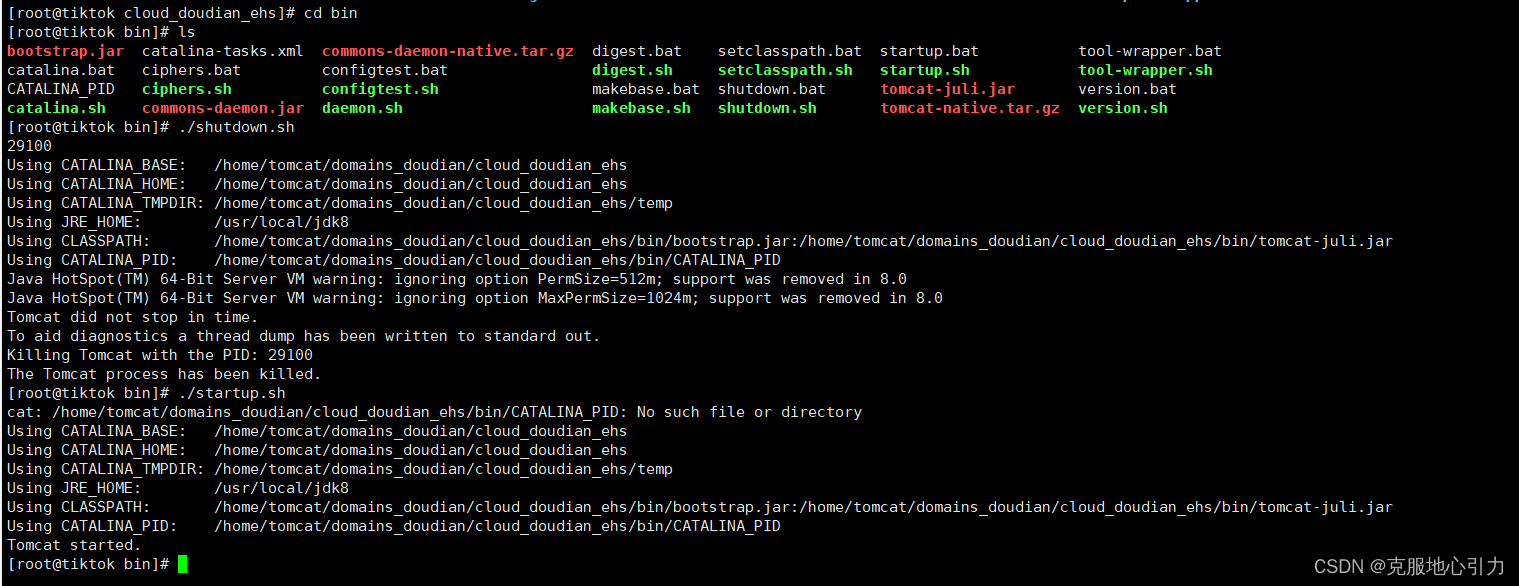
如何打war包,并用war包更新服务器版本
1.打包,我用的maven打包 先执行clean将已经生成的包清除掉 清除完,点package进行打包 控制台输出success,证明打包成功了 文件名.war的后缀就是生成的war包 2.将war包上传致服务器 一般会在war包加上日期版本上传至服务器 解压上传的war…...
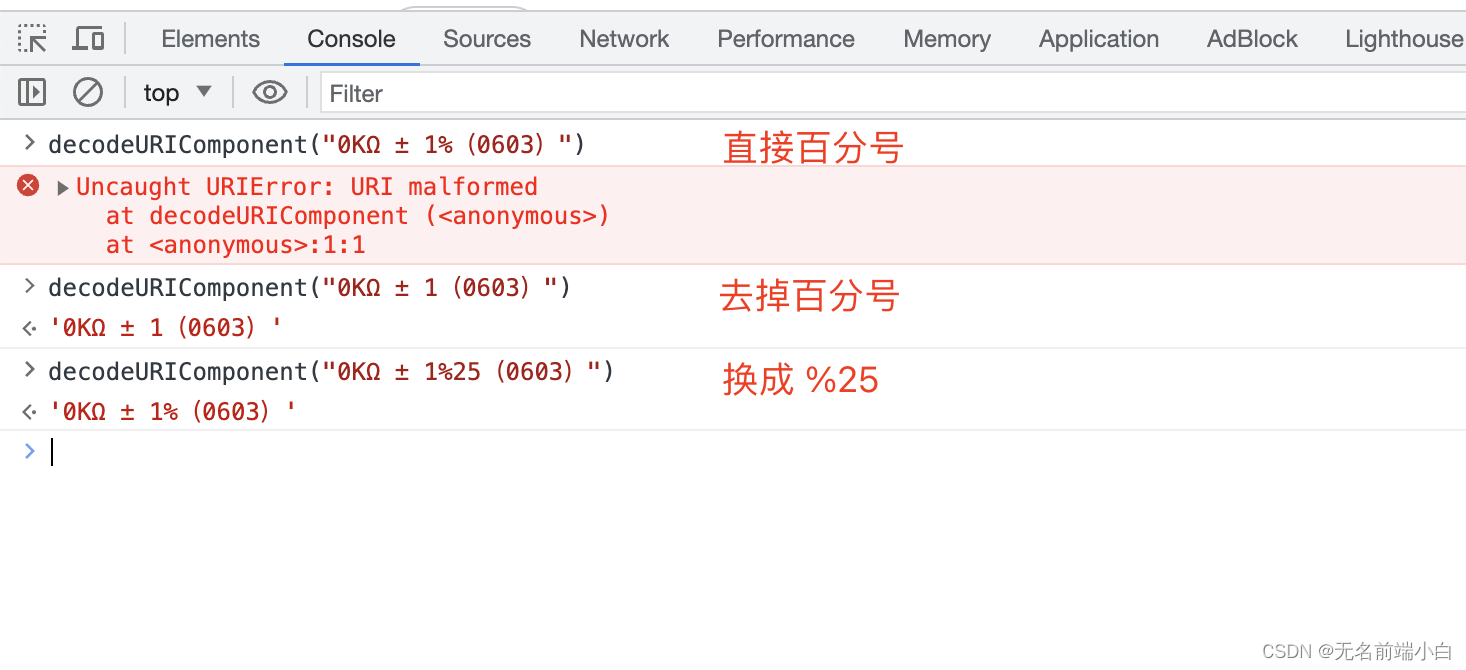
uniApp webview 中调用底座蓝牙打印功能异常
背景: 使用uniApp, 安卓底座 webView 方式开发; 调用方式采用H5 向 底座发送消息, 底座判断消息类型, 然后连接打印机进行打印; 内容通过指令集方式传递给打印机; 过程当中发现部分标签可以正常打印, 但又有部分不行,打印机没反应, 也没有报错; 原因分析: 对比标签内容…...

Mac下安装Jmeter及其配置
一、安装JDK环境 安装方式:mac下配置JDK环境_只看不学的博客-CSDN博客 如果已安装JDK环境即可忽略该步骤,检查方式,在终端输入java -version,如果出现了java版本,即代表已经配置过JDK环境了,如下图所示: …...

js+html实现打字游戏v1
实现逻辑:设置定时器每秒刷新一次,定时器刷新多少次执行一次生成单词操作来决定单词的生成速度,例如初始单词生成速度为1,那么定时器刷新5次才生成一次单词,每个单词用span来装,每组10个单词放到div里。监听…...

Java on VS Code 8月更新|反编译器用户体验优化、新 Maven 项目工作流、代码高亮稳定性提升
作者:Nick Zhu 排版:Alan Wang 大家好,欢迎来到 Visual Studio Code for Java 的 8 月更新!在这篇博客中,我们将为您提供有关反编译器支持的更多改进。此外,我们将展示如何创建没有原型的 Maven 项目以及一…...

划分Vlan时需要注意的问题
网络部分2019年才开始学习的,在学习过程中配置了整个公司的网络,心里才有了一点把握,算是掌握了最基本的。 不会的就上网学,反正网络上什么知识都有,只要有需求就对照着学,很长时间没有学习网络了ÿ…...

【广州华锐互动】利用AR远程指导系统进行机械故障排查,实现远程虚拟信息互动
随着工业自动化和智能化的不断发展,机械故障诊断已经成为了工业生产中的重要环节。为了提高故障诊断的准确性和效率,近年来,AR(增强现实)远程协助技术逐渐应用于机械故障诊断领域。本文将探讨AR远程协助技术在机械故障…...

Spring工具类--CollectionUtils的使用
原文网址:Spring工具类--CollectionUtils的使用_IT利刃出鞘的博客-CSDN博客 简介 本文介绍Spring的CollectionUtils的使用。 CollectionUtils工具类的作用:操作Collection,比如:List、Set。 判断 方法作用static boolean is…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...