支持向量机(一)
文章目录
- 前言
- 分析
- 数据集线性可分情况下的支持向量机
- 原始问题凸优化包解法
- 对偶问题凸优化包解法
- 数据集线性不可分情况下的线性支持向量机与软间隔最大化
前言
- 在支持向量机中,理论逻辑很简单:最大化最小的几何间隔。但是实际编写代码过程中有一个小点需要注意。总是把二分类的类别分为
0和1,这样就导致我的目标函数跟算法描述的就不一样,所以求解结果就不正确。 - 同时还有第二个要注意的就是凸优化包
cvxpy中各种运算的表示方法,比如凸优化中常见的二次方程的表示,变量的默认形状等,要查看官方文档才能熟悉。变量的默认形状为列向量。
参考:
- 李航:统计学习方法
- CVXPY
分析
支持向量机算法中,我们的训练数据除了是两种类别以外,类别的编号也有要求,分别是1、-1,只有这样,我们才能求每个样本所对应的函数间隔 D = y i ( w x i + b ) D=y_i(wx_i+b) D=yi(wxi+b)和几何间隔 D = y i w x i + b ∥ w ∥ 2 D=y_i\frac{wx_i+b}{\|w\|_2} D=yi∥w∥2wxi+b,在这种类别标签的情况下,预测值 w x i + b wx_i+b wxi+b与真实值 y i y_i yi之间的乘积才有意义。
预测与真实相同,乘积才会是大于0的;预测与真实相反,乘积就是小于0的。只有这样后面的目标函数最大化几何间隔才有意义。
重新表述一下可分数据集上支持向量机的目标函数和约束条件:
max λ s.t. y i w x i + b ∥ w ∥ 2 ≥ λ \begin{align*} &\textbf{max}&\lambda \\ &\textbf{s.t.} &y_i\frac{wx_i+b}{\|w\|_2}\ge\lambda \end{align*} maxs.t.λyi∥w∥2wxi+b≥λ
如果我们使用类别标签为0,1,那么当错误分类时,几何间隔为0,无法指导参数修改。所以必须要使用1,-1。
数据集线性可分情况下的支持向量机
此时有两种求法,一种是用原始算法,直接用cvxpy函数包求解原始的这个凸优化问题,并把问题变为下述形式:
max t ∥ w ∥ 2 s.t. y i ( w x i + b ) ≥ t \begin{align*} &\textbf{max}&\frac{t}{\|w\|_2} \\ &\textbf{s.t.} &y_i{(wx_i+b)}\ge t \end{align*} maxs.t.∥w∥2tyi(wxi+b)≥t
由于通过同比例放大w,b可以实现条件中左边的乘积大小的任意变换,所以我们修改t为 1 1 1。上述凸优化问题就变为:
min ∥ w ∥ 2 s.t. y i ( w x i + b ) ≥ 1 \begin{align*} &\textbf{min}&{\|w\|_2} \\ &\textbf{s.t.} &y_i{(wx_i+b)}\ge 1 \end{align*} mins.t.∥w∥2yi(wxi+b)≥1
第二种方法就是将原始问题使用拉格朗日乘子法变换为对偶问题,将加入条件和拉格朗日乘子的拉格朗日函数进行求导,并将求导得到的关系式带入拉格朗日函数,这样就可以得到对偶问题。
原始问题凸优化包解法
import numpy as np
import cvxpy as cp
#生成符合要求的样本数据
np.random.seed(3)
train_x=np.random.randn(2,2)
weight_x=np.random.randn(2)
bias_x=np.random.randn(1)
train_y=np.where(train_x@weight_x+bias_x<0,-1,1).reshape(2,-1)
print(train_x,train_y)
#求解对偶凸优化问题
w=cp.Variable(2)
b=cp.Variable(1)
obj=cp.Minimize(1/2*cp.sum_squares(w))
cons=[train_y[0]*(train_x@w+b)[0]>=1,train_y[1]*(train_x@w+b)[1]>=1]
prob=cp.Problem(obj,cons)
result=prob.solve()
#输出拉格朗日乘子的和最优化的目标函数值以及权重w
print(f'w.value,result,b.value:{w.value,result,b.value}')
结果如下:
[[ 1.78862847 0.43650985][ 0.09649747 -1.8634927 ]] [[-1][ 1]]
w.value,result,b.value:(array([-0.41507783, -0.56418804]), 0.24529887505030906, array([-0.01130633]))
对偶问题凸优化包解法
本例子中我们使用了小规模的数据,只有两个样本,所以这两个样本肯定都是支持向量,也就是对应的拉格朗日乘子都不为0,对于大规模样本数据的情况,如果不在分界面上,那么对应的拉格朗日乘子为0,也就不是支持向量。拉格朗日乘子不为0的肯定就是支持向量。
import numpy as np
import cvxpy as cp
#生成符合要求的样本数据
np.random.seed(3)
train_x=np.random.randn(2,2)
weight_x=np.random.randn(2)
bias_x=np.random.randn(1)
train_y=np.where(train_x@weight_x+bias_x<0,-1,1).reshape(2,-1)
print(train_x,train_y)
#求解对偶凸优化问题
alpha=cp.Variable(2)
obj=cp.Minimize(1/2*cp.quad_form(alpha,(train_x@train_x.T)*(train_y@train_y.T))-cp.sum(alpha))
cons=[alpha>=0,train_y.T@alpha>=0,train_y.T@alpha<=0]
prob=cp.Problem(obj,cons)
result=prob.solve()
#输出拉格朗日乘子的和最优化的目标函数值以及权重w
print(f'alpha.value,result,w:{alpha.value,result,np.array(alpha.value.reshape(2,-1)*train_y*train_x).sum(axis=0)}')
#检验支持向量机求出的分离面是否与这两个样本之间的连线垂直
w=np.array(alpha.value.reshape(2,-1)*train_y*train_x).sum(axis=0)
np.array(train_x[0,:]-train_x[1,:]).reshape(1,-1)@np.array([-w[1]/w[0],1]).reshape(2,-1)
结果如下:
[[ 1.78862847 0.43650985][ 0.09649747 -1.8634927 ]] [[-1][ 1]]
alpha.value,result,w:(array([0.24529888, 0.24529888]), -0.24529887505030898, array([-0.41507783, -0.56418804]))
array([[-4.4408921e-16]])
至于参数b,我们可以通过支持向量所对应的等式求出。
我们可以观察一下原始问题与对偶问题的解答是否一致。
数据集线性不可分情况下的线性支持向量机与软间隔最大化
软间隔顾名思义就是给原来的间隔留下一点宽容量,给那些不容易分正确的留一点余地。同时对于这些余地进行惩罚所得到的分割面,以上面线性可分的数据做演示。
import numpy as np
import cvxpy as cp
#生成符合要求的样本数据
np.random.seed(3)
train_x=np.random.randn(2,2)
weight_x=np.random.randn(2)
bias_x=np.random.randn(1)
train_y=np.where(train_x@weight_x+bias_x<0,-1,1).reshape(2,-1)
print(train_x,train_y)
#求解对偶凸优化问题
w=cp.Variable(2)
b=cp.Variable(1)
softgap=cp.Variable(2)
obj=cp.Minimize(1/2*cp.sum_squares(w)+100*cp.sum(softgap))
cons=[train_y[0]*(train_x@w+b)[0]>=1-softgap[0],train_y[1]*(train_x@w+b)[1]>=1-softgap[1],softgap>=0]
prob=cp.Problem(obj,cons)
result=prob.solve()
#输出拉格朗日乘子的和最优化的目标函数值以及权重w
print(f'w.value,result,b.value,softgap.value:{w.value,result,b.value,softgap.value}')
结果如下:
[[ 1.78862847 0.43650985][ 0.09649747 -1.8634927 ]] [[-1][ 1]]
w.value,result,b.value,softgap.value:(array([-0.41507783, -0.56418804]), 0.24529887505030906, array([-0.01130633]), array([-2.90746355e-22, 1.53881391e-22]))
可以看出在线性可分的的情况下软间隔不起作用。
那么我们制造一些线性不可分的数据,来测试一下。
import numpy as np
import cvxpy as cp
#生成符合要求的样本数据
np.random.seed(3)
train_x=np.array([[0,0],[1,0],[2,0]])
train_y=np.array([-1,1,-1]).reshape(3,-1)
print(train_x,train_y)
#求解对偶凸优化问题
w=cp.Variable(2)
b=cp.Variable(1)
softgap=cp.Variable(3)
obj=cp.Minimize(1/2*cp.sum_squares(w)+0.1*cp.sum(softgap))
cons=[train_y[0]*(train_x@w+b)[0]>=1-softgap[0],train_y[1]*(train_x@w+b)[1]>=1-softgap[1],train_y[2]*(train_x@w+b)[2]>=1-softgap[2],softgap>=0]
prob=cp.Problem(obj,cons)
result=prob.solve()
#输出拉格朗日乘子的和最优化的目标函数值以及权重w
print(f'w.value,result,b.value,softgap.value:{w.value,result,b.value,softgap.value}')
结果如下:
[[0 0][1 0][2 0]] [[-1][ 1][-1]]
w.value,result,b.value,softgap.value:(array([9.07653476e-18, 0.00000000e+00]), 0.2, array([-1.]), array([ 8.59013373e-23, 2.00000000e+00, -8.59013423e-23]))
相关文章:
)
支持向量机(一)
文章目录 前言分析数据集线性可分情况下的支持向量机原始问题凸优化包解法对偶问题凸优化包解法 数据集线性不可分情况下的线性支持向量机与软间隔最大化 前言 在支持向量机中,理论逻辑很简单:最大化最小的几何间隔。但是实际编写代码过程中有一个小点需…...

MyBatis中至关重要的关系映射----全方面介绍
目录 一 对于映射的概念 1.1 三种关系映射 1.2 resultType与resultMap的区别 resultType: resultMap: 二,一对一关联查询 2.1 嵌套结果集编写 2.2 案例演示 三,一对多关联查询 3.1 嵌套结果集编写 3.3 案例演示 四&…...
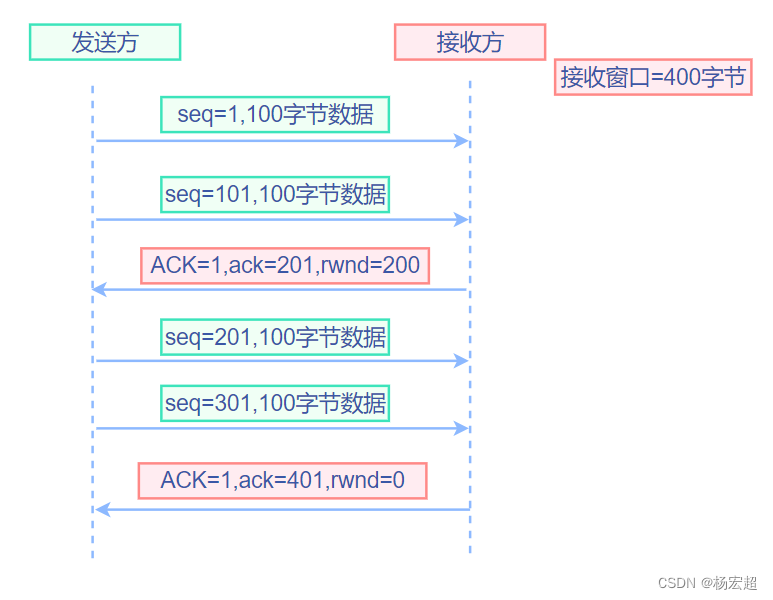
47、TCP的流量控制
从这一节开始,我们学习通信双方应用进程建立TCP连接之后,数据传输过程中,TCP有哪些机制保证传输可靠性的。本节先学习第一种机制:流量控制。 窗口与流量控制 首先,我们要知道的是:什么是流量控制ÿ…...
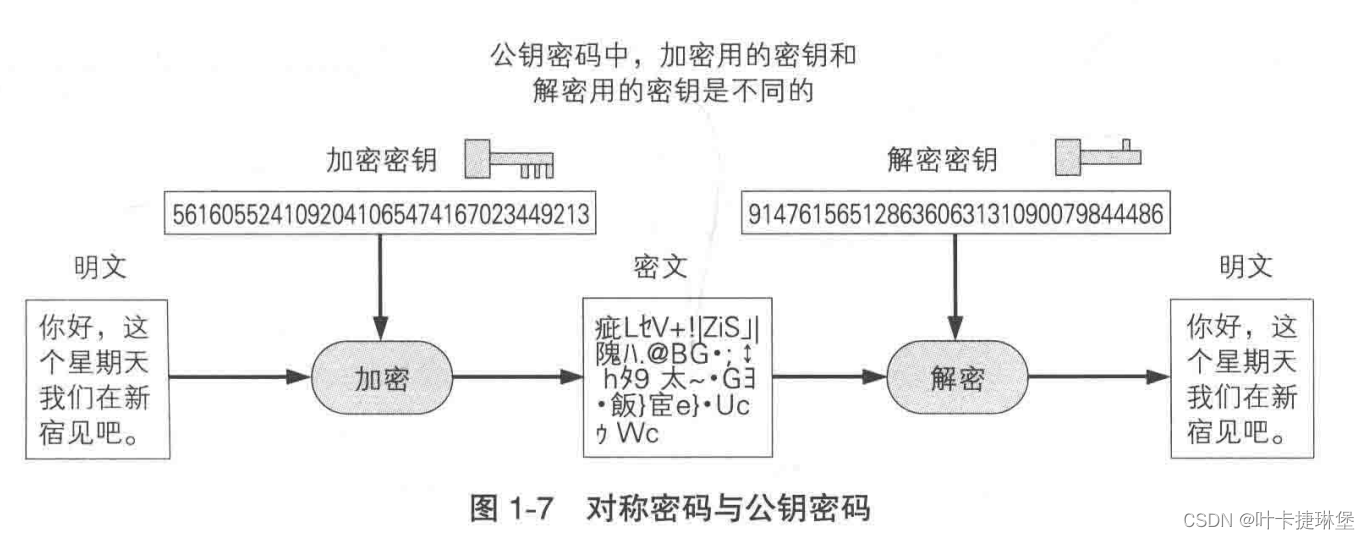
密码学入门——环游密码世界
文章目录 参考书目一、基本概念1.1 本书主要角色1.2 加密与解密 二、对称密码与公钥密码2.1 密钥2.2 对称密码和公钥密码2.3 混合密码技术 三、其他密码技术 参考书目 图解密码技术 第三版 一、基本概念 1.1 本书主要角色 1.2 加密与解密 加密 解密 密码破译 二、对称密…...
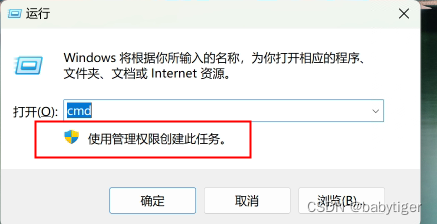
笔记本家庭版本win11上win+r,运行cmd默认没有管理员权限,如何调整为有管理员权限的
华为matebookeGo 笔记本之前有段时间不知怎么回事,打开运行框,没有了那一行“使用管理权限创建此任务”,而且cmd也不再是默认的管理员下的,这很不方便,虽然每次winr ,输入cmd后可以按ctrlshitenter以管理员权限运行&am…...

MavenCentral库发布记录
最近发布了 Android 路由库 URouter,支持 AGP8、ActivityResult启动等特性。 把提交到 Maven Central 过程记录一下。 一、注册 Sonatype 账号,新建项目 注册 https://issues.sonatype.org 登录后,新建项目: 相关选项&…...
的使用)
小程序进阶-env(safe-area-inset-bottom)的使用
一、简介 env(safe-area-inset-bottom)和env(safe-area-inset-top)是CSS中的变量,用于获取设备底部和顶部安全区域的大小。 所谓的安全区域就是指在iPhone X及以上的设备中,为避免被屏幕的“刘海”和“Home Indicator”所遮挡或者覆盖的有效区域区域&am…...
移动端App持续集成体系构建实战
这里写目录标题 一、目标1、前言2、优势:3、涉及技术点4、目标 二、测试app构建、打包过程1、安卓打包的环境要求 三、演示安卓源码打包四、演示安卓App部署1、前提条件2、命令控制apk安装与卸载 五、安卓UI自动化测试1、Appium app自动化测试-Python2、实现的验证点…...

Mybatis的关联关系配置一对一,一对多,多对多的映射关系
目录 关联关系映射 一对一关联: 一对多关联: 多对多关联: 导入数据库表 一对多 一对一 多对多 关联关系映射 关联关系映射在Mybatis中主要通过三种方式实现:一对一关联和一对多关联及多对多关联。 一对一关联:…...
计算机竞赛 基于深度学习的中文情感分类 - 卷积神经网络 情感分类 情感分析 情感识别 评论情感分类
文章目录 1 前言2 情感文本分类2.1 参考论文2.2 输入层2.3 第一层卷积层:2.4 池化层:2.5 全连接softmax层:2.6 训练方案 3 实现3.1 sentence部分3.2 filters部分3.3 featuremaps部分3.4 1max部分3.5 concat1max部分3.6 关键代码 4 实现效果4.…...
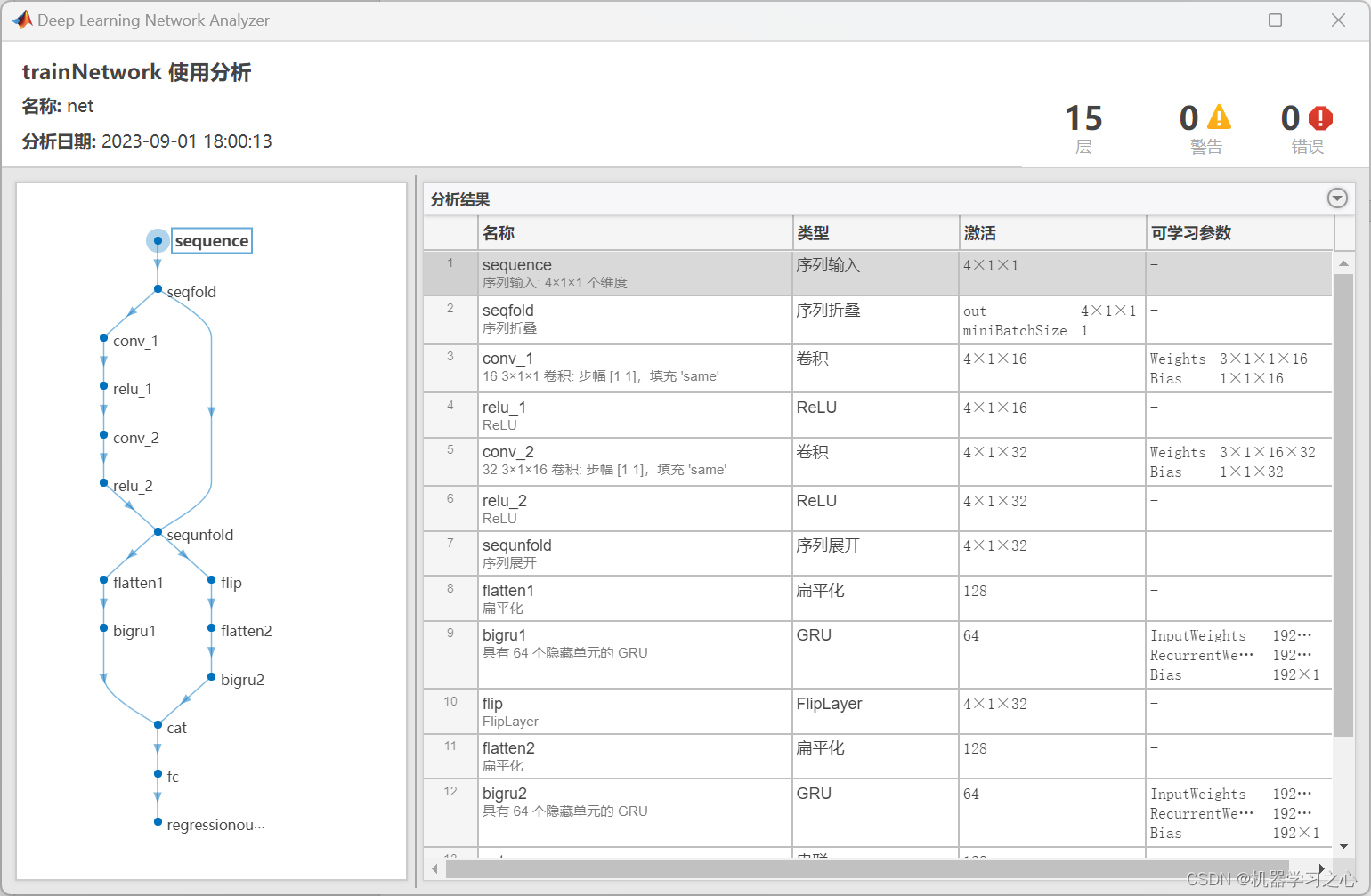
时序预测 | MATLAB实现CNN-BiGRU卷积双向门控循环单元时间序列预测
时序预测 | MATLAB实现CNN-BiGRU卷积双向门控循环单元时间序列预测 目录 时序预测 | MATLAB实现CNN-BiGRU卷积双向门控循环单元时间序列预测预测效果基本介绍程序设计参考资料 预测效果 基本介绍 1.MATLAB实现CNN-BiGRU卷积双向门控循环单元时间序列预测; 2.运行环境…...

[Rust GUI]0.10.0版本iced代码示例 - progress_bar
-1 字体支持 iced0.10.0 仅支持指定系统内置字体(iced默认字体中文会乱码) iced0.10.0 手动加载字体的功能已经砍了,想手动加载就用0.9.0版本,文档0.9.0版本 想显示中文则需要运行在一个自带字体的Windows系统上。而且这个字体最好不要钱。 (Windows闲着…...
使用vue-pdf出现的卡顿,空白,报错,浏览器崩溃解决办法
如果想直接知道解决办法,请翻到最下面 今天,接到了一个新的需求,我们公司的PDF展示卡住了,导致浏览器直接奔溃。我也刚来公司不久,就去看看是怎么发生的,公司前同事用的vue-pdf,刚开始以为是文…...
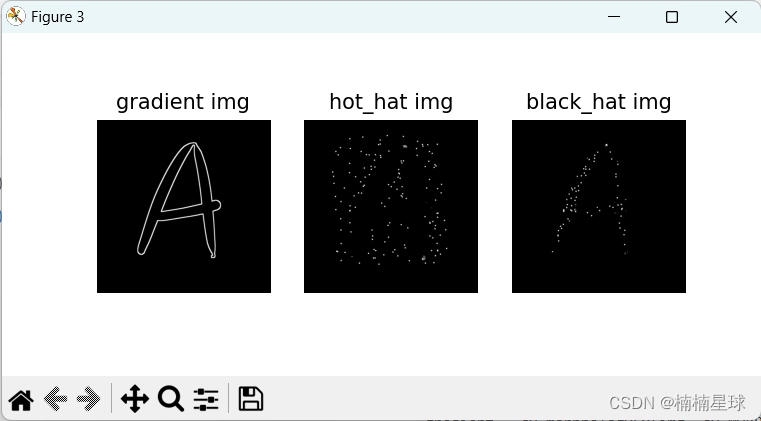
(笔记七)利用opencv进行形态学操作
(1)程序清单 形态学操作是一种图像处理技术,它基于数学形态学理论,用于改变图像的形状和结构。它主要通过结构元素的腐蚀和膨胀操作来实现。 #!/usr/bin/env python # -*- coding:utf-8 -*- """ author: LIFEI t…...

Spring是什么?
什么是Spring 我知道你现在可能迫不及待地想要开始编写Spring应用了。我向你保证,在本章结束之前,你肯定能够开发一个简单的Spring应用。但首先,我将使用Spring的一些基础概念为你搭建一个舞台,帮助你理解Spring是如何运转起来的…...

电梯SIP-IP五方对讲管理系统
电梯SIP-IP五方对讲管理系统 是深圳锐科达精心打磨的一款IP数字信号对讲设备,是在传统电梯对讲系统基础上的一次全新升级,突破了模拟、FM调频系统存在的技术障碍,实现联网;在模/数交替的过程中,继承了模拟、FM调频系统的优点&…...

leetcode283移动零
题目: 给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。 请注意 ,必须在不复制数组的情况下原地对数组进行操作。 示例 1: 输入: nums [0,1,0,3,12] 输出: [1,3,12,0,0]示例 2: 输入:…...

Docker 部署SpringBoot项目,使用外部配置文件启动项目
一、Springboot项目引入配置文件的方式: 第一种是在jar包的同一目录下建一个config文件夹,然后把配置文件放到这个文件夹下; 第二种是直接把配置文件放到jar包的同级目录; 第三种在classpath下建一个config文件夹,然后…...
电子半导体行业电能质量监测与治理系统解决方案 安科瑞 许敏
摘要:在国家鼓励半导体材料国产化的政策导向下,本土半导体材料厂商不断提升半导体产品技术水平和研发能力,逐渐打破了国外半导体厂商的垄断格局,推进中国半导体材料国产化进程,促进中国半导体行业的发展。半导体产品的…...
pdfh5在线预览pdf文件
前言 pc浏览器和ios的浏览器都可以直接在线显示pdf文件,但是android浏览器不能在线预览pdf文件,如何预览pdf文件? Github: https://github.com/gjTool/pdfh5 Gitee: https://gitee.com/gjTool/pdfh5 使用pdfh5预览pdf 编写预览页面 <…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...
