OJ题库:计算日期到天数转换、打印从1到最大的n位数 、尼科彻斯定理
前言:在部分大厂笔试时经常会使用OJ题目,这里对《华为机试》和《剑指offer》中的部分题目进行思路分析和讲解,希望对各位读者有所帮助。
题目来自牛客网,欢迎各位积极挑战:
HJ73:计算日期到天数转换_牛客网
JZ17:打印从1到最大的n位数_牛客网
HJ76:尼科彻斯定理_牛客网
目录
HJ73 计算日期到天数转换
题目相关消息
题目描述
输入描述
输出描述
示例
分析问题解决思路
具体实现细节:
完整代码实现
JZ17 打印从1到最大的n位数
题目相关消息
描述
示例
分析问题解决思路
具体实现细节
完整代码实现
HJ76 尼科彻斯定理
题目相关信息
题目描述
输入描述
输出描述
示例
分析问题解决思路
具体实现细节
完整代码实现
HJ73 计算日期到天数转换
题目相关消息
题目描述
根据输入的日期,计算是这一年的第几天。
保证年份为4位数且日期合法。
进阶:时间复杂度: O(n) ,空间复杂度: O(1)
输入描述
输入一行,每行空格分割,分别是年,月,日
输出描述
输出是这一年的第几天
示例
输入:2012 12 31
输出:366
输入:1982 3 4
输出:63
分析问题解决思路
题目让我们输出有多少天,只要解决了以下俩个小问题,问题就迎刃而解了
- 闰年的情况,我们需要判断输入是否是闰年,在闰年内,2月是29天,这是与正常平年不同的情况,因此我们需要设计和函数来判断是否是闰年
- 我们在判断的时候应该使用累加的思想,从1月累加到目标月,但是值得注意的一点是,目标月不能直接加当前月份总的天数,应该加上用户输入的天数
具体实现细节:
首先我们需要先设计一个判断闰年的函数,如果是闰年就返回1,不是就返回0,方便后续进行调用判断:
int judgeleapyear(int year)
{if ((year % 4 == 0 && year % 100 != 0) || (year % 400 == 0)){return 1;}elsereturn 0;
}主函数方面,我们定义一个整形变量 days 来记录从这一年的第一天到现在一共有多少天,定义 year, month, day三个整形变量分别来记录用户输入的值,从一月开始遍历到目标月,不包含目标月,如果是大月 days 就加31,如果是小月就加30,另外在2月的时候,使用一个 if 语句来判断当前 2 月有多少天
//大月if ((months == 1) || (months == 3) || (months == 5) || (months == 7) || (months == 8) || (months == 10) || (months == 12)){days += 31;}//小月else if ((months == 4) || (months == 6) || (months == 9) || (months == 11)){days += 30;}//二月else{//润年if (ret == 1){days += 29;}//平年else{days += 28;}}完整代码实现
//HJ73
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>int judgeleapyear(int year)
{if ((year % 4 == 0 && year % 100 != 0) || (year % 400 == 0)){return 1;}elsereturn 0;
}int main()
{int year = 0;int month = 0;int day = 0;int days = 0;scanf("%d %d %d", &year, &month, &day);//判断是否是闰年int ret = judgeleapyear(year);//从一月加到目标月for (int months = 1; months < month; months++){//大月if ((months == 1) || (months == 3) || (months == 5) || (months == 7) || (months == 8) || (months == 10) || (months == 12)){days += 31;}//小月else if ((months == 4) || (months == 6) || (months == 9) || (months == 11)){days += 30;}//二月else{//润年if (ret == 1){days += 29;}//平年else{days += 28;}}}days += day;printf("%d", days);return 0;
}JZ17 打印从1到最大的n位数
题目相关消息
描述
输入数字 n,按顺序打印出从 1 到最大的 n 位十进制数。比如输入 3,则打印出 1、2、3 一直到最大的 3 位数 999。
- 用返回一个整数列表来代替打印
- n 为正整数,0 < n <= 5
示例
输入:1
返回值:[1,2,3,4,5,6,7,8,9]
注意,这道题目是接口题,我们只需要完善题目给出的函数就可以了,将需要返回的值返回就完成了
int* printNumbers(int n, int* returnSize) {}
分析问题解决思路
首先,我们需要明确一件事,这道题是接口题,我们不能像普通的 ACM 模式的题那样写个循环直接打印,我们需要将数据放在一块空间内,然后将其返回
既然是要放在空间内,那我们就使用 malloc 函数来动态开辟空间,最后在这些空间内逐个赋值就可以了
具体实现细节
首先我们得先明确数值的范围,如下所示的过程中,我们不难发现,这是次方的关系,也就是说 10^n-1 就是数值的最大值
- 1 位数的数值就是 1~9
- 2 位数的数值就是 1~99
- 3 位数的数值就是 1~999
- 4 位数的数值就是 1~9999
那么在这里我们就使用 <math.h> 头文件中的库函数 pow 来实现次方的效果,这样我们就获得了数值的大小范围
//返回数组元素的个数*returnSize = pow(10, n) - 1;
接下来就是动态分配空间,在这里需要注意的是要进行强制类型转化,不然会因为前后类型不一致导致 bug,一个整形大小是 sizeof(int),一共有 *returnsize 个整形
//动态分配空间int* arr = (int*)malloc(*returnSize * sizeof(int));//malloc(字节数)
最后赋值就非常简单了,使用 for 循环实现就可以了
//赋值for (int i = 0; i < *returnSize; ++i){*(arr + i) = i + 1;}
完整代码实现
int* printNumbers(int n, int* returnSize)
{//返回数组元素的个数*returnSize = pow(10, n) - 1;//动态分配空间int* arr = (int*)malloc(*returnSize * sizeof(int));//malloc(字节数)//赋值for (int i = 0; i < *returnSize; ++i){*(arr + i) = i + 1;}//返回return arr;
}
HJ76 尼科彻斯定理
题目相关信息
题目描述
验证尼科彻斯定理,即:任何一个整数m的立方都可以写成m个连续奇数之和
例如:
1^3=1
2^3=3+5
3^3=7+9+11
4^3=13+15+17+19
输入一个正整数m(m≤100),将m的立方写成m个连续奇数之和的形式输出
数据范围: 1≤m≤100
进阶:时间复杂度:O(m) ,空间复杂度:O(1)
输入描述
输入一个int整数
输出描述
输出分解后的string
示例
输入:6
输出:31+33+35+37+39+41
分析问题解决思路
首先,我们必须得理解这个题目背后的数学原理,我们举例如下
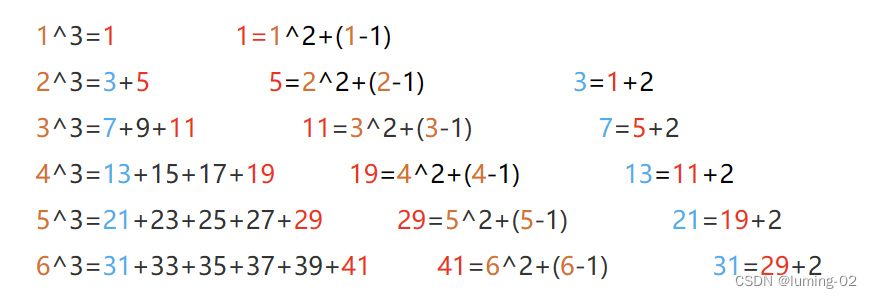
我们会发现,在多项式中的第一项和最后一项是有迹可循的,我们对于第一项和最后一项的总结如下
- 第一项:(n-1)^2+((n-1)-1)+2
- 最后一项:n^2+(n-1)
具体实现细节
我们先使用俩个变量来找到刚才所描述的第一项和最后一项
int m_first = 0;int m_end = 0;m_first = (m - 1) * (m - 1) + (((m - 1) - 1) + 2);m_end = (m * m) + (m - 1);
在找到第一项后,我们就可以使用遍历累加来打印了,在尼科彻斯定理表示的多项式中,多项式的数量和要表达的整数m是一样的,都是m,基于此,我们就可以使用循环了,每一次都打印一个奇数,然后在让这个奇数加 2,最后再直接打印最后一项
for (int i = 0; i < (m - 1); i++){printf("%d+", m_first);m_first += 2;}printf("%d", m_end);完整代码实现
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<math.h>void math_N(int m)
{int m_first = 0;int m_end = 0;m_first = (m - 1) * (m - 1) + (((m - 1) - 1) + 2);m_end = (m * m) + (m - 1);for (int i = 0; i < (m - 1); i++){printf("%d+", m_first);m_first += 2;}printf("%d", m_end);
}int main()
{int m = 0;scanf("%d", &m);math_N(m);return 0;
}本次分享就到此结束了,希望我的分享对您有所帮助
相关文章:
OJ题库:计算日期到天数转换、打印从1到最大的n位数 、尼科彻斯定理
前言:在部分大厂笔试时经常会使用OJ题目,这里对《华为机试》和《剑指offer》中的部分题目进行思路分析和讲解,希望对各位读者有所帮助。 题目来自牛客网,欢迎各位积极挑战: HJ73:计算日期到天数转换_牛客网 JZ17:打印…...
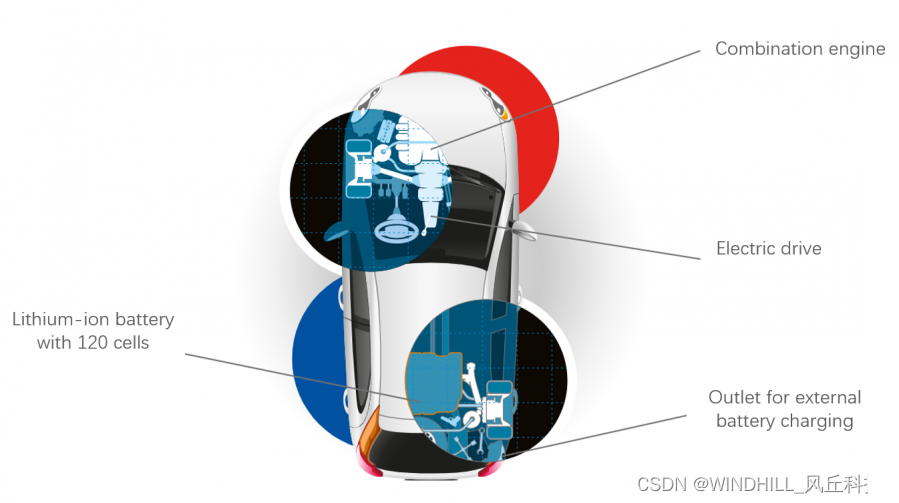
混合动力汽车耐久测试
一 背景 整车厂可通过发动机和电机驱动的结合为多款车型提供混合动力驱动技术。汽车集成电机驱动可大大减少二氧化碳的排放,不仅如此,全电动驱动或混合动力驱动的汽车还将使用户体验到更好的驾驶感受,且这种汽车可通过电动机来实现更快的加速…...
useRef 定义的 ref 在控制台可以打印但是页面不生效?
useRef 是一个 React Hook,它能让你引用一个不需要渲染的值。 点击计时器 点击按钮后在控制台可以打印但是页面不生效。 useRef 返回的值在函数组件中不会自动触发重新渲染,所以控制台可以显示变化而按钮上无法显示 ref.current的变化。 import { use…...
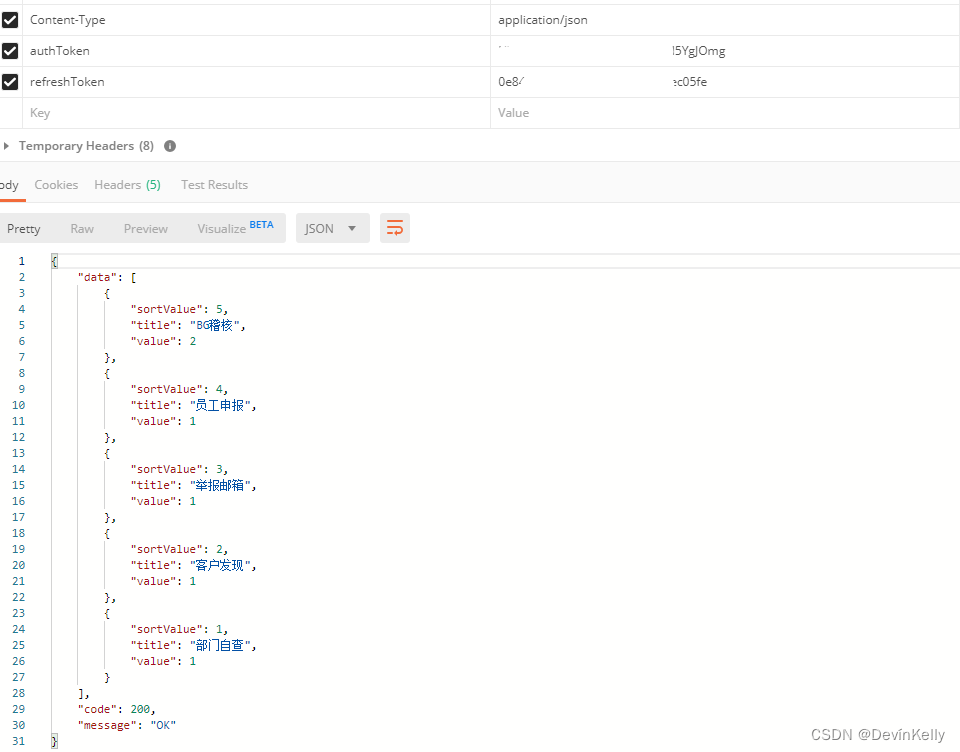
【Java 动态数据统计图】动态数据统计思路案例(动态,排序,动态数组(重点推荐))七(129)
需求:前端根据后端的返回数据:画统计图; 说明: 1.X轴为地域,Y轴为地域出现的次数; 2. 动态展示(有地域展示,没有不展示,且高低排序) Demo案例: …...

Cell Reports | 揭开METTL14在介导m6A修饰中的神秘面纱
m6A被认为是最丰富的mRNA修饰,广泛分布在大多数真核生物中,包括哺乳动物、植物、昆虫、酵母和某些病毒。m6A修饰的沉积和去除之间的动态平衡对于正常的生物过程和发育至关重要,如失调通常与癌症等疾病有关。m6A修饰由m6A甲基转移酶复合物&…...

297. 二叉树的序列化与反序列化
题目描述 序列化是将一个数据结构或者对象转换为连续的比特位的操作,进而可以将转换后的数据存储在一个文件或者内存中,同时也可以通过网络传输到另一个计算机环境,采取相反方式重构得到原数据。 请设计一个算法来实现二叉树的序列化与反序…...
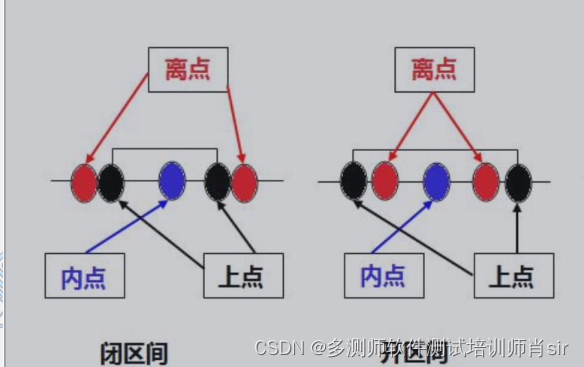
肖sir__设计测试用例方法之边界值03_(黑盒测试)
设计测试用例方法之边界值 边界点定义 上点:边界上的点 离点:离上点最近的点(即上点左右两边最邻近的点) 内点:在域范围内的点 案例:qq号:5-12位 闭区间: 离点:5 位 &…...

功能测试常用的测试用例大全
登录、添加、删除、查询模块是我们经常遇到的,这些模块的测试点该如何考虑 1)登录 ① 用户名和密码都符合要求(格式上的要求) ② 用户名和密码都不符合要求(格式上的要求) ③ 用户名符合要求,密码不符合要求(格式上的要求) ④ 密码符合要求,…...

css利用flex分配剩余高度出现子组件溢出问题
1.利用flex分配剩余高度/宽度 情景:父组件高度一定,子组件中,其他子组件高度固定,一个子组件高度不确定(页面滚动列表) .father{display: flex;flex-direction: column;.son1{height: 200px;}.son2{//或 …...
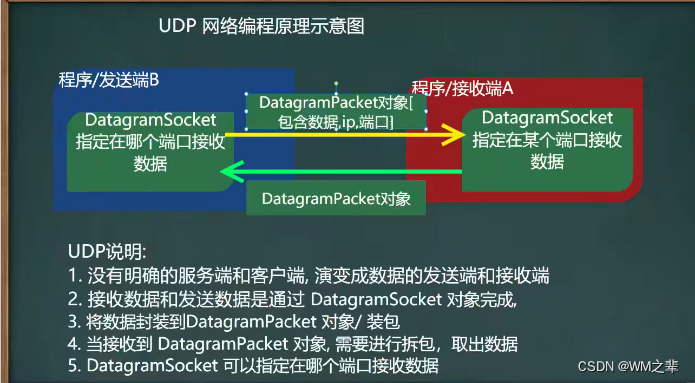
Java中的网络编程------基于Socket的TCP编程和基于UDP的网络编程,netstat指令
Socket 在Java中,Socket是一种用于网络通信的编程接口,它允许不同计算机之间的程序进行数据交换和通信。Socket使得网络应用程序能够通过TCP或UDP协议在不同主机之间建立连接、发送数据和接收数据。以下是Socket的基本介绍: Socket类型&…...

【【STM32-29正点原子版本串口发送传输实验】
STM32-29正点原子版本串口发送传输实验 通过串口接收或发送一个字符 例程目的 开发板上我们接入的是实现异步通信的UART接口 USB转串口原理图 我们一步步分析 PA9是串口1 的发送引脚 PA10是串口1 的接受引脚 。因为我们现在只是用到异步收发器功能,所以我们现…...

【面试题精讲】什么是websocket?如何与前端通信?
有的时候博客内容会有变动,首发博客是最新的,其他博客地址可能会未同步,认准https://blog.zysicyj.top 首发博客地址 系列文章地址 什么是WebSocket? WebSocket是一种在Web应用程序中实现双向通信的协议。它允许在客户端和服务器之间建立持久…...
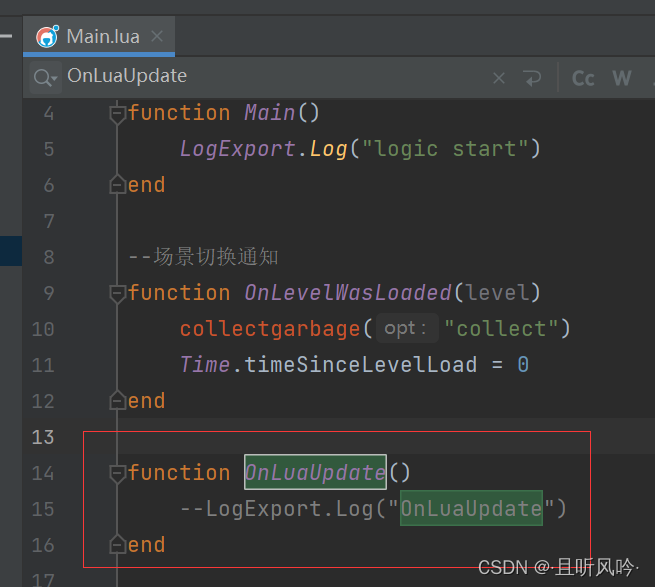
unity tolua热更新框架教程(2)
Lua启动流程 增加脚本luamain,继承luaclient 建立第一个场景GameMain,在对象GameMain挂载脚本LuaMain,启动场景 看到打印,lua被成功加载 lua入口及调用堆栈 这里会执行main.lua文件的main函数 C#接口导出 在此处配置C#导出的代码 …...
【0904作业】QT 完成登陆界面跳转到聊天室+完成学生管理系统的查找和删除功能
一、完成登陆界面跳转到聊天室 1> 项目结构 2> 源码 ① .pro ②main #include "mywnd.h" #include"chatCli.h" #include <QApplication>int main(int argc, char *argv[]) {QApplication a(argc, argv);MyWnd w;w.show();Form f;QObject::co…...

ceph源码阅读 buffer
ceph::buffer是ceph非常底层的实现,负责管理ceph的内存。ceph::buffer的设计较为复杂,但本身没有任何内容,主要包含buffer::list、buffer::ptr、buffer::hash。这三个类都定义在src/include/buffer.h和src/common/http://buffer.cc中。 buffe…...

基本介绍——数据挖掘
1.数据挖掘的定义 数据挖掘是采用数学的、统计的、人工智能和神经网络等领域的科学方法,如记忆推理、聚类分析、关联分析、决策树、神经网络、基因算法等技术,从大量数据中挖掘出隐含的、先前未知的、对决策有潜在价值的关系、模式和趋势,并…...

Navicat连接postgresql时出现‘datlastsysoid does not exist‘报错
当使用 Navicat 连接 PostgreSQL 数据库时出现 ‘datlastsysoid does not exist’ 的错误报错,这可能是由于 Navicat 版本与 PostgreSQL 版本不兼容所致。 这是因为在较新的 PostgreSQL 版本中移除了 ‘datlastsysoid’ 列,但可能较旧版本的 Navicat 尚…...

冯诺依曼体系结构/什么是OS?
一、体系结构图 示意图 控制器可以控制其它4个硬件,四个硬件直接可以进行数据传输。 5大硬件 但是这些个体需要用“线”连接。 为什么要有存储器? 如果没有,实际速度则为输入、输出设备的速度。 加上后,变为内存的速度。&#…...

SD卡/TF卡简记
文章目录 MicroSD卡与SD卡关系与区别对比NM卡、XQD卡、CFexpress卡SD规格标识FAQ拍摄1080p或2k视频需要什么速度的sd卡?拍摄4k视频需要什么速度的sd卡?拍摄8k视频需要什么速度的sd卡? MicroSD卡与SD卡关系与区别 MicroSD卡原名为Trans-flash…...

Dockerfile COPY的奇怪行为:自动解包一级目录
记录一下今天遇到的坑:Dockerfile 这两天在部署项目的时候,新加进去了一个驱动,需要将2个文件夹以及1个文件COPY进镜像,大刀阔斧一个Dockerfile就写完了,结果COPY进去的文件有问题,Dockerfile的内容如下&am…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...
