leetcode88合并两个有序数组
题目:
给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。
请你 合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。
注意:最终,合并后数组不应由函数返回,而是存储在数组 nums1 中。为了应对这种情况,nums1 的初始长度为 m + n,其中前 m 个元素表示应合并的元素,后 n 个元素为 0 ,应忽略。nums2 的长度为 n 。
示例 1:
输入:nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3 输出:[1,2,2,3,5,6] 解释:需要合并 [1,2,3] 和 [2,5,6] 。 合并结果是 [1,2,2,3,5,6] ,其中斜体加粗标注的为 nums1 中的元素。
示例 2:
输入:nums1 = [1], m = 1, nums2 = [], n = 0 输出:[1] 解释:需要合并 [1] 和 [] 。 合并结果是 [1] 。
示例 3:
输入:nums1 = [0], m = 0, nums2 = [1], n = 1 输出:[1] 解释:需要合并的数组是 [] 和 [1] 。 合并结果是 [1] 。 注意,因为 m = 0 ,所以 nums1 中没有元素。nums1 中仅存的 0 仅仅是为了确保合并结果可以顺利存放到 nums1 中。
提示:
nums1.length == m + nnums2.length == n0 <= m, n <= 2001 <= m + n <= 200-109 <= nums1[i], nums2[j] <= 109
解决:
解法1:利用Arrays中的sort方法排序直接求解
public void merge(int[] nums1,int m,int[] nums2,int n) {for(int i=0;i<n;i++){nums1[m+i]=nums2[i];}Arrays.sort(nums1);}快速排序,时间复杂度为O((m+n)log(m+n))。代码效率不是特别高。其最大的问题是,题目给的数组元素本来是有序的,但这样混起来之后用sort排序相当于又重新排序了一遍,即没有充分利用元素的有序性。
解法2:用双指针
每次从两个数组的头部各取出一个数比较,把比较小的结果复制到临时数组中,再把比较小数所在数组指针后移一位。把两个数组元素都复制到临时数组后,临时数组的结果就是排序以后的结果了。再把临时数组的元素复制到nums1。这样的话两个数组都只循环了一遍,时间复杂度为O(m+n)。空间复杂度也是O(m+n)。
public void merge(int[] nums1,int m,int[] nums2,int n) {int k=m+n;int[] temp=new int[k];for(int index=0,nums1Index=0,nums2Index=0;index<k;index++){if(nums1Index>=m) {//nums1数组已经取完,接下来完全取nums2数组的值temp[index]=nums2[nums2Index++];}else if(nums2Index>=n){temp[index]=nums1[nums1Index++];}else if(nums1[nums1Index]<nums2[nums2Index]){//nums1数组元素值小于nums2数组元素值,取nums1数组的值temp[index]=nums1[nums1Index++];}else{temp[index]=nums2[nums2Index++];}}for(int i=0;i<k;i++){nums1[i]=temp[i];}}解法3:用双指针,倒序处理
把nums2的最后一个元素与nums1的有效的最后一个元素比较,把大的放在nums1的最后一个0的位置。再把刚才的指针往前移一位,再比较这样就用到nums1的空间了,不用引入临时数组。这样时间复杂度为O(m+n),空间复杂度为O(m)。
public void merge(int[] nums1,int m,int[] nums2,int n) {int k=m+n;for(int index=k-1,nums1Index=m-1,nums2Index=n-1;index>=0;index--){if(nums1Index<0) {//nums1数组已经取完,接下来完全取nums2数组的值nums1[index]=nums2[nums2Index--];}else if(nums2Index<0){break;}else if(nums1[nums1Index]>nums2[nums2Index]){//nums1数组元素值大于nums2数组元素值,取nums1数组的值nums1[index]=nums1[nums1Index--];}else{nums1[index]=nums2[nums2Index--];}}}加油加油^_^
相关文章:

leetcode88合并两个有序数组
题目: 给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。 请你 合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。 注意:最终&…...

Ceph入门到精通-Nginx 大量请求 延迟优化
优化nginx以处理大量请求并减少延迟可以通过以下几种方法实现: 调整worker_processes和worker_connections参数:增加worker_processes值可以增加nginx的进程数量,提高并发处理能力。增加worker_connections参数的值可以增加每个worker进程可…...

Vulnstack----5、ATTCK红队评估实战靶场五
文章目录 一 环境搭建二 外网渗透三 内网信息收集3.1 本机信息收集3.2 域内信息收集 四 横向移动4.1 路由转发和代理通道4.2 抓取域用户密码4.3 使用Psexec登录域控4.4 3389远程登录 五、痕迹清理 一 环境搭建 1、项目地址 http://vulnstack.qiyuanxuetang.net/vuln/detail/7/ …...

QT 5.8
QT与Qt Creator,前者是框架,类似与MFC,而后者是QT的编译器,也可以使用Visual studio编辑,编译需要其他的 Index of /new_archive/qt/5.8/5.8.0...
AIGC+思维导图:提升你的学习与工作效率的「神器」
目录 一、产品简介 二、功能介绍 2.1 AI一句话生成思维导图 2.2百万模版免费用 2.3分屏视图,一屏读写 2.4团队空间,多人协作 2.5 云端跨平台化 2.6 免费够用,会员功能更强大 2.7 支持多种格式的导入导出 三、使用教程 3.1 使用AI…...
javaScript:DOM元素的获取(静态/动态获取)
目录 一.dom元素获取的意义与使用场景 使用场景(绝大多数js操作都需要dom操作) 总结/疑问解答! 二.DOM元素获取的常用方法(重点) 获取dom元素(动态) document.gerElementbyId() docume…...
数据结构前言
一、什么是数据结构? 数据结构是计算机存储、组织数据的方式。数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。 上面是百度百科的定义,通俗的来讲数据结构就是数据元素集合与数据元素集合或者数据元素与数据元素之间的组成形式。 举个…...

Docker基于alpine带glibc的小型容器image
由于程序是C写的,gc编译,找了几个容器,生成比较小的是debianslim和ubuntu,生成后的大小分别为88MB,和91MB,还是太大了,于是想起一些小型容器如busybox或者alpine自己装glibc,但是试了…...
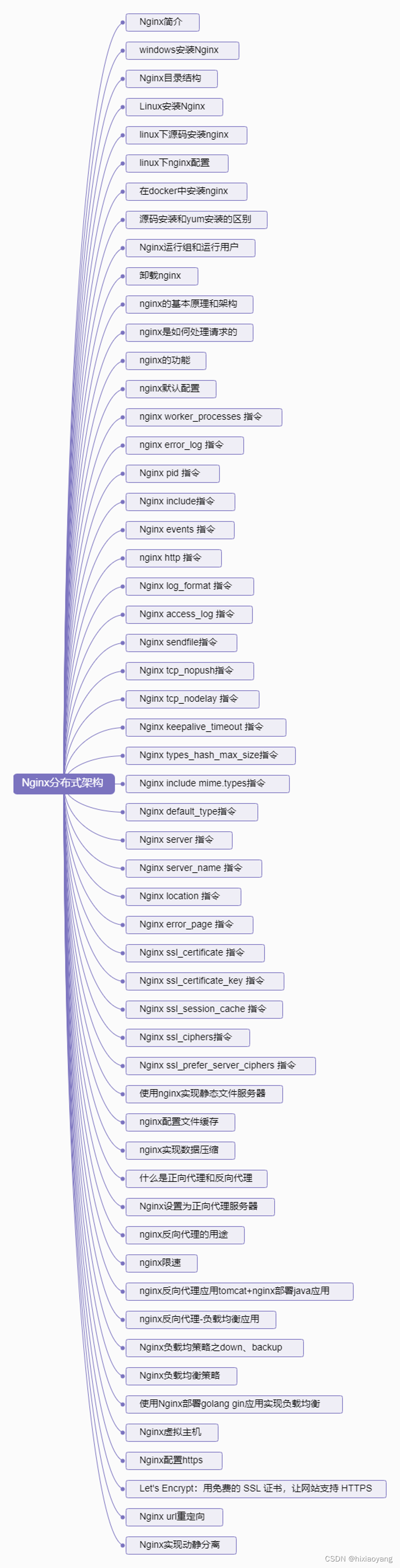
Nginx教程
Nginx教程 01-Nginx简介02-windows安装Nginx03-Nginx目录结构04-Linux安装Nginx05-linux下源码安装nginx06-linux下nginx配置07-在docker中安装nginx08-源码安装和yum安装的区别09-Nginx运行组和运行用户10-卸载nginx11-nginx的基本原理和架构12-nginx是如何处理请求的13-nginx…...

直播预约|哪吒汽车岳文强:OEM和Tier1如何有效对接网络安全需求
信息安全是一个防护市场。如果数字化程度低,数据量不够,对外接口少,攻击成本高,所获利益少,自然就没有什么攻击,车厂因此也不需要在防护上花费太多成本。所以此前尽管说得热闹,但并没有太多真实…...

hiveserver2经常挂断的原因
hiveserver2经常挂断的原因 HiveServer2 经常挂断可能有多种原因,以下是一些可能导致挂断的常见原因: 资源不足:HiveServer2 需要足够的内存和 CPU 资源来处理查询请求。如果资源不足,可能会导致 HiveServer2 挂断。请确保在配置…...

openeuler 23.03 安装mysql 8.X
遇到一堆问题:直接从mysql官下载,都不行。下列是失败的: mysql80-community-release-el8-1.noarch.rpm mysql-8.0.34-1.el8.x86_64.rpm-bundle.tar mysql-8.1.0-1.el9.x86_64.rpm-bundle.tar 后来想从openeuler下载应该靠谱:ht…...

网络安全—0基础学习笔记(黑客)
一、前言 1.这是一条坚持的道路,三分钟的热情可以放弃往下看了. 2.多练多想,不要离开了教程什么都不会了.最好看完教程自己独立完成技术方面的开发. 3.有时多 google,baidu,我们往往都遇不到好心的大神,谁会无聊天天给你做解答. 4.遇到实在搞不懂的,可以先放放,以后再来解决. …...

react HashRouter 与 BrowserRouter 的区别及使用场景
一、简介 在单页面应用中,如何在切换页面后,不刷新浏览器呢?为了解决这个问题,有两种方法,就是hash路由模式、history路由模式,而 react router 的两种路由就是使用这两种路由模式。 二、区别 HashRouter…...

痞子衡嵌入式:恩智浦i.MX RT1xxx系列MCU硬件那些事(2.3)- 串行NOR Flash下载算法(J-Link工具篇)
https://www.cnblogs.com/henjay724/p/13770137.html 大家好,我是痞子衡,是正经搞技术的痞子。今天痞子衡给大家介绍的是J-Link工具下i.MXRT的串行NOR Flash下载算法设计。 在i.MXRT硬件那些事系列之《在串行NOR Flash XIP调试原理》一文中,痞…...
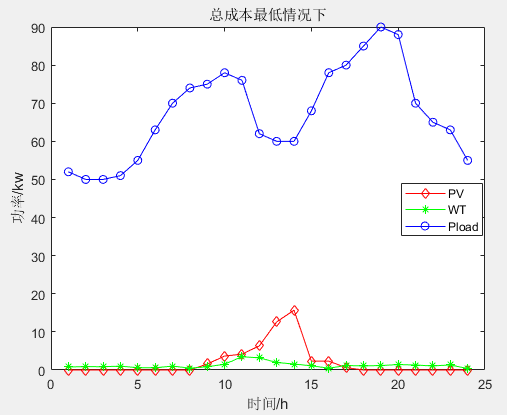
多目标应用:基于多目标向日葵优化算法(MOSFO)的微电网多目标优化调度MATLAB
一、微网系统运行优化模型 参考文献: [1]李兴莘,张靖,何宇,等.基于改进粒子群算法的微电网多目标优化调度[J].电力科学与工程, 2021, 37(3):7 二、多目标向日葵优化算法 多目标向日葵优化算法(Multi-objective sunflower optimization,MOS…...

智能安全科技,Vatee万腾为您服务
在智能科技的引领下,Vatee万腾将为您点亮投资之路,助您在金融市场中抓住机遇,实现财务目标。作为一家融合科技与投资的先锋平台,Vatee万腾致力于为投资者提供智能化的投资方案和支持。 Vatee万腾以其先进的智能科技为基础…...

Scala中的类型检查和转换,以及泛型,scala泛型的协变和逆变
Scala中的类型检查和转换,以及泛型 类型检查和转换 说明 (1) obj.isInstanceOf[T]:判断 obj 是不是T 类型。 (2) obj.asInstanceOf[T]:将 obj 强转成 T 类型。 (3) cla…...
【数据结构】C语言队列(详解)
前言: 💥🎈个人主页:Dream_Chaser~ 🎈💥 ✨✨专栏:http://t.csdn.cn/oXkBa ⛳⛳本篇内容:c语言数据结构--C语言实现队列 目录 一.队列概念及结构 1.1队列的概念 1.2队列的结构 二.队列的实现 2.1头文…...
【数据结构初阶】一. 复杂度讲解
相关代码gitee自取: C语言学习日记: 加油努力 (gitee.com) 接上期: 学C的第三十四天【程序环境和预处理】_高高的胖子的博客-CSDN博客 1 . 算法效率 (1). 什么是数据结构: 数据结构(Data Structure)是计算机存储、…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...

恶补电源:1.电桥
一、元器件的选择 搜索并选择电桥,再multisim中选择FWB,就有各种型号的电桥: 电桥是用来干嘛的呢? 它是一个由四个二极管搭成的“桥梁”形状的电路,用来把交流电(AC)变成直流电(DC)。…...
