直方图统计增强方法
直方图统计增强方法的原理:
直方图统计增强是一种基于像素值分布的图像增强技术,通过调整像素值的分布来增强图像的对比度和细节。其原理是根据图像的直方图信息,将原始像素值映射到一个新的像素值域,从而改变图像的亮度和对比度。
直方图统计增强方法的意义:
这种方法的目的是改善图像的视觉效果,使得图像中的细节更加清晰可见,从而提高图像在视觉上的识别和分析能力。通过将图像的像素值重新分布,使得图像的动态范围更好地覆盖了整个像素值域,凸显了图像中的细节,增强了图像的信息内容。
适用场景:
直方图统计增强方法在以下场景中特别适用:
- 低对比度图像: 当图像的亮度范围分布不均匀,即图像的对比度较低时,直方图统计增强可以使得图像的像素值分布更加均匀,增强图像的对比度。
- 局部对比度调整: 有时候图像的一部分区域可能亮度较低,另一部分区域亮度较高。直方图统计增强可以通过针对不同区域使用不同的增强参数,实现局部对比度的调整。
- 图像细节增强: 当图像中的细节由于亮度过低或过高而不易分辨时,直方图统计增强可以突出这些细节,使得它们更加清晰可见。
公式:
直方图统计增强的基本公式如下:
给定一个原始图像 I ( x , y ) I(x, y) I(x,y),其像素值为 i i i,进行直方图统计增强后的图像为 I enhanced ( x , y ) I_{\text{enhanced}}(x, y) Ienhanced(x,y),其像素值为 i ′ i' i′。增强函数可以表示为:
i ′ = T ( i ) = round ( c ⋅ i ) i' = T(i) = \text{round}(c \cdot i) i′=T(i)=round(c⋅i)
其中, c c c是增强常数,可以通过调整来控制增强的强度。一般情况下, c > 1 c > 1 c>1 用于增强亮度, c < 1 c < 1 c<1用于降低亮度。函数 ( \text{round} ) 将结果四舍五入到最接近的整数,确保结果在合法的像素值范围内。
另外,为了避免像素值越界,通常还会使用截断操作将增强后的像素值 ( i’ ) 限制在图像像素值域的合法范围内(通常是 [0, 255]):
i ′ = { 0 if c ⋅ i < 0 255 if c ⋅ i > 255 round ( c ⋅ i ) otherwise i' = \begin{cases} 0 & \text{if } c \cdot i < 0 \\ 255 & \text{if } c \cdot i > 255 \\ \text{round}(c \cdot i) & \text{otherwise} \end{cases} i′=⎩ ⎨ ⎧0255round(c⋅i)if c⋅i<0if c⋅i>255otherwise
这样,直方图统计增强就可以通过调整增强常数 c c c 来改变图像的亮度和对比度,从而实现图像的增强,代码如下所示:
import cv2
import matplotlib.pyplot as plt
import numpy as npdef enhanceHistStat(image, const):enhanced_image = np.clip(image * const, 0, 255).astype(np.uint8)return enhanced_imagedef enhance_Histstat(image):# 读取图像image = cv2.imread(image, flags=0)if image is None:print('Unable to load input_image!')returnelse:# 计算比例因子maxImg = image.max()maxROI = image[12:120, 12:120].max()const = maxImg / maxROI# 调用增强函数image_HSE = enhanceHistStat(image, const)image_Equ=cv2.equalizeHist(image)plt.figure(figsize=(10,6))plt.subplot(131),plt.title("Original image"),plt.axis('off')plt.imshow(image,cmap='gray',vmin=0,vmax=255)plt.subplot(132),plt.title("Global equalize histogram"),plt.axis('off')plt.imshow(image_Equ,cmap='gray',vmin=0,vmax=255)plt.subplot(133),plt.title("Histogram statistic enhance"),plt.axis('off')plt.imshow(image_HSE,cmap='gray',vmin=0,vmax=255)plt.show()imgfile1='./Images/cat.jpg'
enhance_Histstat(imgfile1)
相关文章:

直方图统计增强方法
直方图统计增强方法的原理: 直方图统计增强是一种基于像素值分布的图像增强技术,通过调整像素值的分布来增强图像的对比度和细节。其原理是根据图像的直方图信息,将原始像素值映射到一个新的像素值域,从而改变图像的亮度和对比…...

字节二面:如果高性能渲染十万条数据?
前言 最近博主在字节面试中遇到这样一个面试题,这个问题也是前端面试的高频问题,作为一名前端开发工程师,我们虽然可能很少会遇到后端返回十万条数据的情况,但是了解掌握如何处理这种情况,能让你对前端性能优化有更深的…...
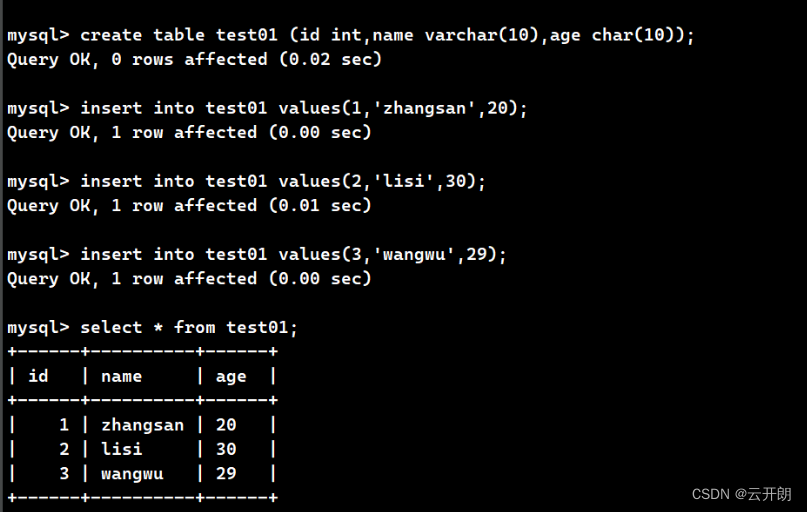
Mysql高阶语句(二)
一、设置别名(alias ——>as) 在 MySQL 查询时,当表的名字比较长或者表内某些字段比较长时,为了方便书写或者 多次使用相同的表,可以给字段列或表设置别名。使用的时候直接使用别名,简洁明了࿰…...
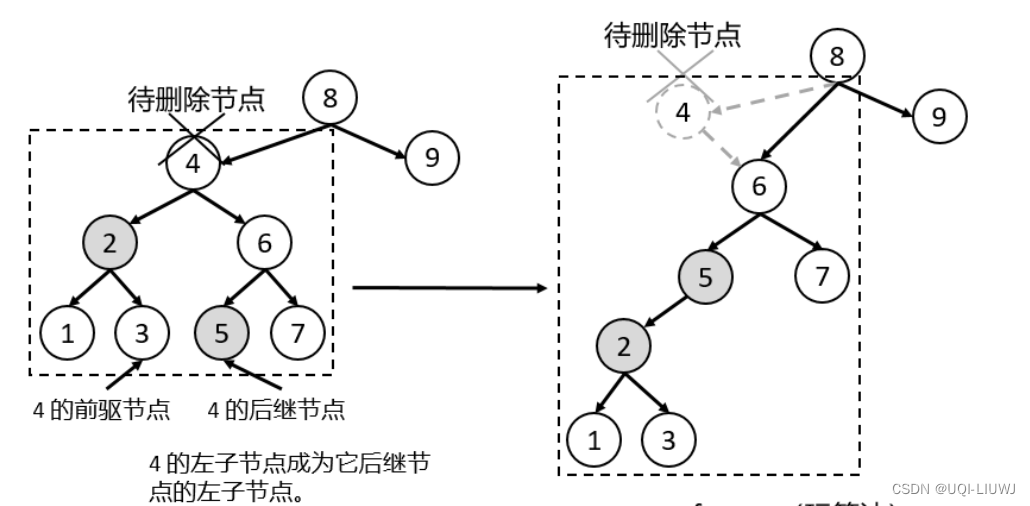
算法笔记 二叉搜索树
二叉搜索树(Binary Search Tree,简称 BST)是一种数据结构,用于存储具有可比较键(通常是数字或字符串)的元素 1 结构特点 节点结构:每个节点都有一个键和两个子节点(左子节点和右子…...

微软牵手Linux:Ubuntu“系统”上架win10应用商店啦
导读继SUSE Linux登陆之后,Ubuntu今天正式以UWP应用的身份上架Win10应用商店。Windows Insider用户升级到Win10秋季创意者更新预览版Build 16190及以上就可以下载和安装Ubuntu系统应用。一旦下载和安装完Ubuntu应用后,它将开始在你的Windows10 PC上安装U…...

leetcode做题笔记126. 单词接龙 II
按字典 wordList 完成从单词 beginWord 到单词 endWord 转化,一个表示此过程的 转换序列 是形式上像 beginWord -> s1 -> s2 -> ... -> sk 这样的单词序列,并满足: 每对相邻的单词之间仅有单个字母不同。转换过程中的每个单词 s…...

windows下运行springboot的jar包,修改替换class文件,修改配置文件application,打包
在windows下跑springboot的jar包,经常会用到一些命令行和操作。 1、修改配置文件(以application.yml为例) #提取文件 jar xvf mqtt-10.1.0.jar BOOT-INF/classes/application.yml#将文件装回jar包 jar uvf mqtt-10.1.0.jar BOOT-INF/classe…...
)
PMD 检查java代码:可以去掉无用的括号(UselessParentheses)
这个规则的优先级比较低。 https://docs.pmd-code.org/pmd-doc-6.55.0/pmd_rules_java_codestyle.html#uselessparentheses 无用的括号可以去掉。当然,有时候为了避免理解起来困难,加上括号反而更加清晰。 例如: public static short calc…...

【数据结构练习】栈的面试题集锦
目录 前言: 1.进栈过程中可以出栈的选择题 2.将递归转化为循环 3.逆波兰表达式求值 4.有效的括号 5. 栈的压入、弹出序列 6. 最小栈 前言: 数据结构想要学的好,刷题少不了,我们不仅要多刷题,还要刷好题&#x…...
简单工厂模式概述和使用
目录 一、简单工厂模式简介1. 定义2. 使用动机 二、简单工厂模式结构1.模式结构2. 时序图 三、简单工厂的使用实例四、简单工厂模式优缺点五、简单工厂模式在Java中的应用 一、简单工厂模式简介 原文链接 1. 定义 简单工厂模式(Simple Factory Pattern):又称为静…...

软件工程概述
软件工程概述 软件工程指的是应用计算机科学、数学及管理科学等原理,以工程化的原则和方法来解决软件问题的工程,目的是提高软件生产效率、提高软件质量、降低软件成本。 1. 计算机软件 计算机软件指的是计算机系统中的程序及其文档。程序是计算任务的…...
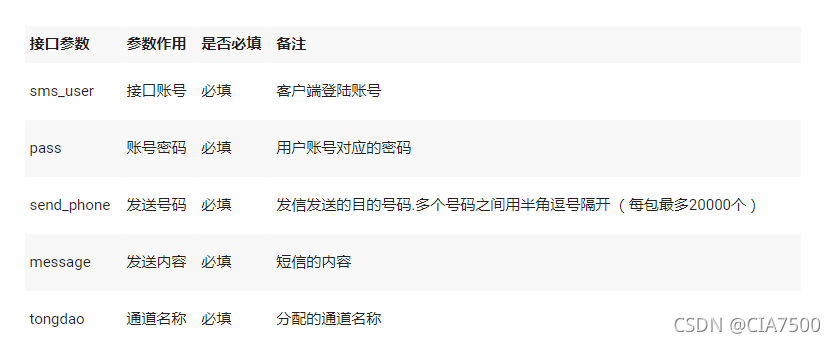
国际网页短信软件平台搭建定制接口说明|移讯云短信系统
国际网页短信软件平台搭建定制接口说明|移讯云短信系统 通道路由功能介绍 支持地区通道分流,支持关键字,关键词通道分流,支持白名单独立通道,支持全网通道分流,支持通道可发地区设置,通道路由分组&#x…...
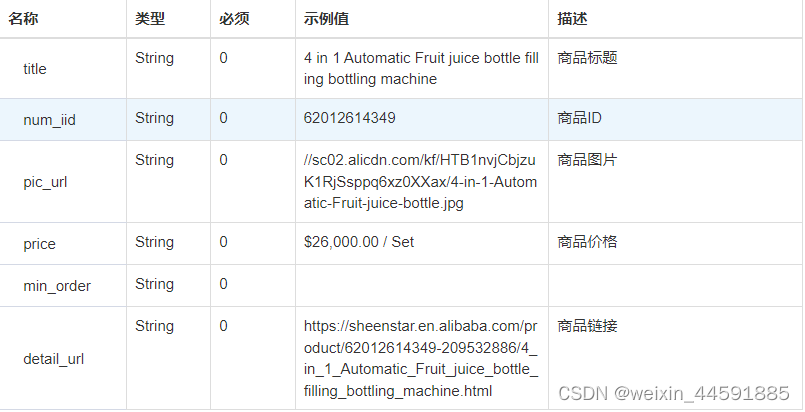
Java“牵手”阿里巴巴店铺所有商品API接口数据,通过店铺ID获取整店商品详情数据,阿里巴巴店铺所有商品API申请指南
阿里巴巴平台店铺所有商品数据接口是开放平台提供的一种API接口,通过调用API接口,开发者可以获取阿里巴巴整店的商品的标题、价格、库存、月销量、总销量、库存、详情描述、图片、价格信息等详细信息 。 获取店铺所有商品接口API是一种用于获取电商平台…...

【Sql】把数据库字段用函数根据逗号分裂成列表,然后判断列表中是否包含目标值
【Sql】把数据库字段用函数根据逗号分裂成列表,然后判断列表中是否包含目标值 【1】问题描述【2】Oracle内置函数解决【3】mysql的内置函数INSTR()【4】mysql的内置函数FIND_IN_SET() 【1】问题描述 数据库中【库信息db】和【集群信息cluster】是一对多的关系&…...

docker基本命令记录
Docker 是一个开源的容器技术,它允许开发人员将应用程序及其所有依赖项打包到一个容器中,然后轻松地在任何地方部署和运行。以下是 Docker 的一些基本操作: 基础操作: 启动 Docker:service docker start停止 Docker:service docker stop查看 Docker 信息:docker info容器操作…...

web之利用延迟实现复杂动画、animation
文章目录 效果图htmlstyleJavaScript 效果图 html <div class"container"><div class"ball"></div><input type"range" min"0" max"1" step"0.01" /> </div>style body {display…...
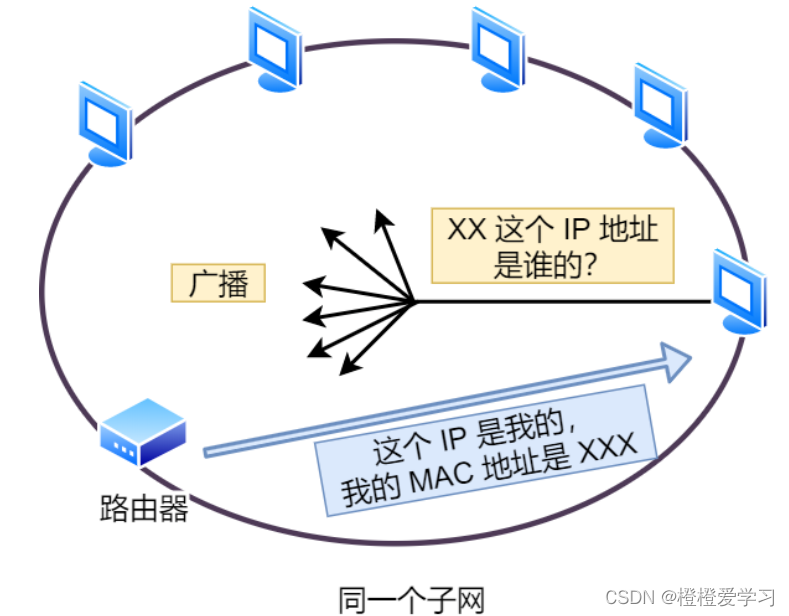
TCP 和 UDP 的区别、TCP 是如何保证可靠传输的?
先来介绍一些osi七层模型 分为应用层、表示层、会话层、运输层、网络层、链路层、物理层。 应用层(数据):确定进程之间通信的性质以及满足用户需要以及提供网络和用户应用,为应用程序提供服务,DNS,HTTP,HTTPS…...

鼠标悬停阴影的效果被旁边div挡住的解决办法
出现的问题 需求要求鼠标悬停某个图片上有阴影效果,但阴影被旁边相邻的div挡住了,如图所示 解决方案 给悬停的这块div增加2个css属性 $(this).css(position, relative); $(this).css(z-index, 200);新的效果如图所示 一直写后端,前端的…...

Go用两个协程交替打印100以内的奇偶数
方式1(使用无缓冲的channel) package mainimport ( "fmt" "time")var flagChan make(chan int)func wokr1() { for i : 1; i < 100; i { flagChan <- 666 // 塞入 if i%2 1 { fmt.Println("协程1打印:", i) …...

css 文字单行多行超出长度后显示 ...
0.超出… 1、单行文本超出 <div class"content">测试数据:css单行文本超出显示省略号--------</div><style> .content{width: 200px;height: 200px;overflow:hidden;white-space: nowrap;text-overflow: ellipsis;-o-text-overflow:el…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...
