Less的强大变量用法
less中的变量应用十分强大,可以灵活的应用到各种不同需求的场景。
一,属性值变量
声明:sass声明变量是用$符号,而less声明变量是用@符号
作用域:也区分为全局变量和局部变量,如果引用的变量有定义局部变量,则优先取局部变量。这里没有闭包的概念!
例如:
@wd: 12px;
@bgColor: #ff005a;.container {width: @wd;background-color: @bgColor; // 就近取局部变量#FFF@bgColor: #FFF; // 局部变量
}二,属性名变量
声明:与属性值变量一致,使用@变量名。属性名定义变量可以大大减少代码量
引用:@{变量名} - 需要用大括号包裹
示例:
// 定义属性名变量
@bdCol: background-color;.main {@{bdCol}: #FFF; // 引用
}// 编译后
.main {background-color: #FFF;
}三,选择器变量
声明:声明方式与值变量类似,主要作用是让选择器变成动态
引用:@{变量名}
示例:
// 定义选择器变量
@outDiv: #warp; // 变量直接定义id选择器
@innerDiv: main; // 变量定义选择器的名称// 引用
@{outDiv} {width: 100%;margin: 20px;
}.@{innerDiv} { // 引用选择器变量名称,并定义class选择器color: #fff;
}
#@{outDiv} {color: #333;
}// 编译后
#warp {width: 100%;margin: 20px;
}.main {color: #fff;
}#warp {color: #333;
}四,url变量
声明:与普通值变量用法一致,但变量值要加引号。为图片等资源文件的url定义变量。
引用:@{变量名}
示例:
// 定义url变量
@logo: "../assects/img";.img {background: url("@{logo}/logo.png"); // 引用,通过大括号、字符串拼接
}// 编译后
.img {background: url("../assects/img/logo.png");
}五,同时声明变量名和变量值
声明:@变量名: {属性名:属性值}。看上去像是封装一组声明好的变量和值,类似于mixin。
引用:@变量名() - 后面加小括号
示例:
// 定义样式属性名和属性值的变量
@bgWhite: {background: #FFF;}
// 引用
.main {@bgWhite();
}
// 编译后
.main {background: #FFF;
}// 定义一组样式的变量
@Rules {color: red;font-size: 12px;
}
// 引用
.container {@Rules();
}
// 编译后
.container {color: red;font-size: 12px;
}六,变量运算
说明:less的变量支持简单的加减乘除算术运算。
使用方式:
加减运算以第一个值的单位为基准
乘除运算单位必须统一
示例:
@wd: 100px;
@color: #112233;// 计算应用
.main {width: @wd + 20; // 120px.header {width: @wd - 10px * 2; // 80pxfont-size: 14px;color: @color*2; // #224466}
}七,动态变量-用变量定义变量
说明:即动态定义要引用的变量名称
引用:还是通过@符号,但是引用变量的变量,需要两个@。
示例:
@wd: 100px;
@labelWd: "wd"; // 定义labelWd变量需要引用的变量名为wd// 引用
.title {width: @@labelWd; // 即@wd > 100px;
}相关文章:

Less的强大变量用法
less中的变量应用十分强大,可以灵活的应用到各种不同需求的场景。 一,属性值变量 声明:sass声明变量是用$符号,而less声明变量是用符号 作用域:也区分为全局变量和局部变量,如果引用的变量有定义局部变量&…...

【相机标定】opencv python 标定相机内参时不计算 k3 畸变参数
文章目录 1. 背景2. 完整的 opencv python 标定相机内参过程3. 选择是否计算畸变参数 k3 1. 背景 畸变参数 k3 通常用于描述径向畸变的更高阶效应,即在需要高精度的应用中可以用到,一般的应用中 k1, k2 足矣。 常见的应用中, orbslam3 中是否…...
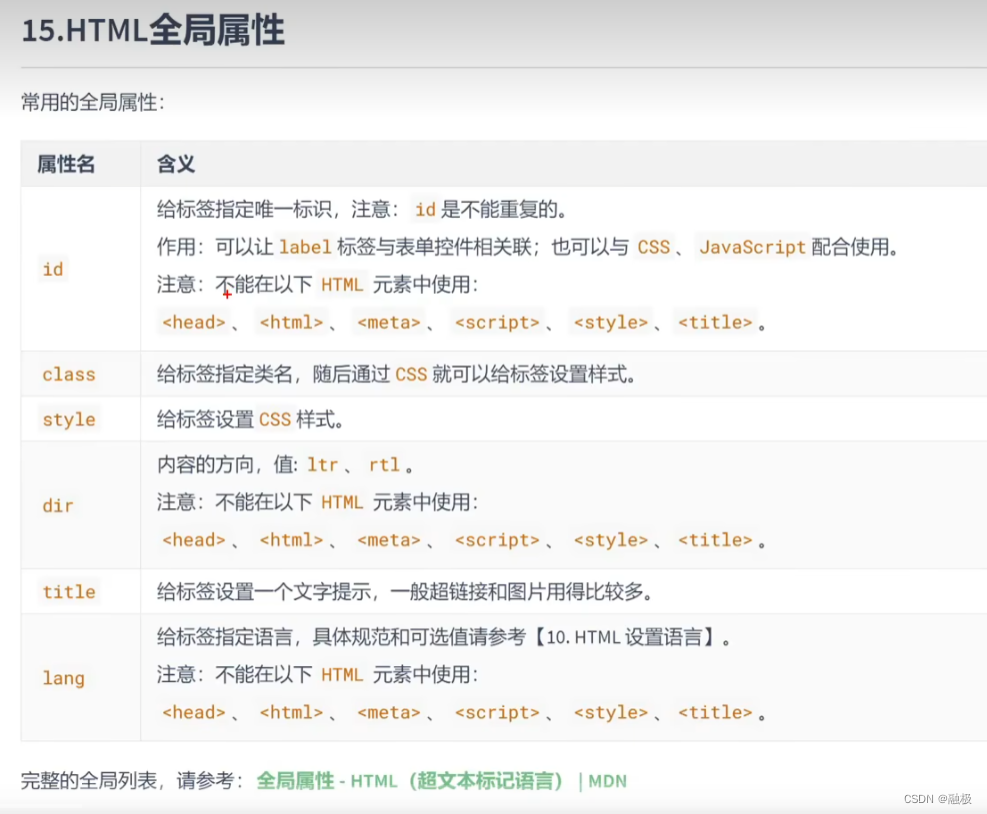
html 标签简介
概述 标签的效果不重要,重要的是标签的语义。 文本标签 文本标签用于包裹:词汇、短语等。排版标签,比如div,p,h1等。排版标签更宏观(大段的文字),文本标签更微观(词汇、短语)。文…...

dos汇编总结
前言: 计组课本需要学习汇编,可惜自己看不太懂。这里发现一个学习方法交给大家。其实新手可能一些抽象表示难理解,这里我把我学习的疑问点以及思路记录一下。 要点: 这里我以题为例给大家分析 输出输入对应大写字母的小写字母 …...

四川玖璨电子商务有限公司:短视频有什么运营
根据短视频有什么运营,短视频的拍摄工具多种多样。无论是在手机上拍摄还是使用专业摄影设备,拍摄短视频的目的都是为了吸引观众的注意力和提升内容的质量。从小花费到高投入,在不断发展的短视频行业中,拍摄方法也得到了不断创新和…...
混合查询多家快递,快速掌握物流信息
在现代社会,快递服务已成为我们日常生活的重要组成部分。无论是购物还是文件传递,我们都需要快递服务的帮助。然而,不同的快递公司需要不同的查询方法,这无疑增加了我们的查询难度。因此,有没有一种方法可以让我们一次…...

独立站新手引流,谷歌SEO工具汇总
俗话说“工欲善其事,必先利其器”,做谷歌SEO也一样,要想做好并提升SEO效果,卖家就需要了解并利用好SEO工具。那我们今天就来盘点一下,常用的SEO工具有哪些吧~ 网站检测工具 1、PageSpeed Insights:这是谷…...

SpringMvc 与 Lombok 碰撞导致 JSON 反序列化失败
SpringMvc 与 Lombok 中 JSON 反序列化失败 错误复现_1 Data public class User{private Long id;private boolean isOk; }RequestMapping public R<User> getUser(RequestBody User user){return R.success(user); }// 前端传参 - {"id": 123456789,"i…...

怎么样显卡叠加,什么是NVIDIA 显卡 非公、公版、涡轮卡
1、显存叠加的问题,因为这个跟是否是深度学习无关: 先说一下显存叠加的问题,因为这个跟是否是深度学习无关:一台机器有多张显卡,显存不会叠加!显卡里面包含了显存、cache、计算单元、通信等,每…...

CentOS安装Elasticsearch集群
前言 之前使用的ES集群是其他公司维护,没有机会安装,后来做其他项目,终于有机会安装ES集群,简单记录一下备用 一、安装jdk 安装jdk1.8就可以,可以参考另一篇文章,这里就不细说了 二、修改系统参数 如果在…...

计算机专业毕业生指南
在大四毕业时,完成计算机毕业设计需要一定的计划和组织。以下是一些建议,帮助你在三个月内快速完成毕业设计: 选择一个合适的主题: 选择一个你感兴趣的主题,这将激发你的热情,使你更有动力完成项目。 确保…...

Springboot集成Docker并将镜像推送linux服务器
案例使用springboot项目,在IDEA 中集成Docker生成镜像,并将镜像发布到linux服务器 具体步骤如下: 1、Centos7安装Docker 更新系统的软件包列表 sudo yum update安装Docker所需的软件包和依赖项: sudo yum install docker完成…...
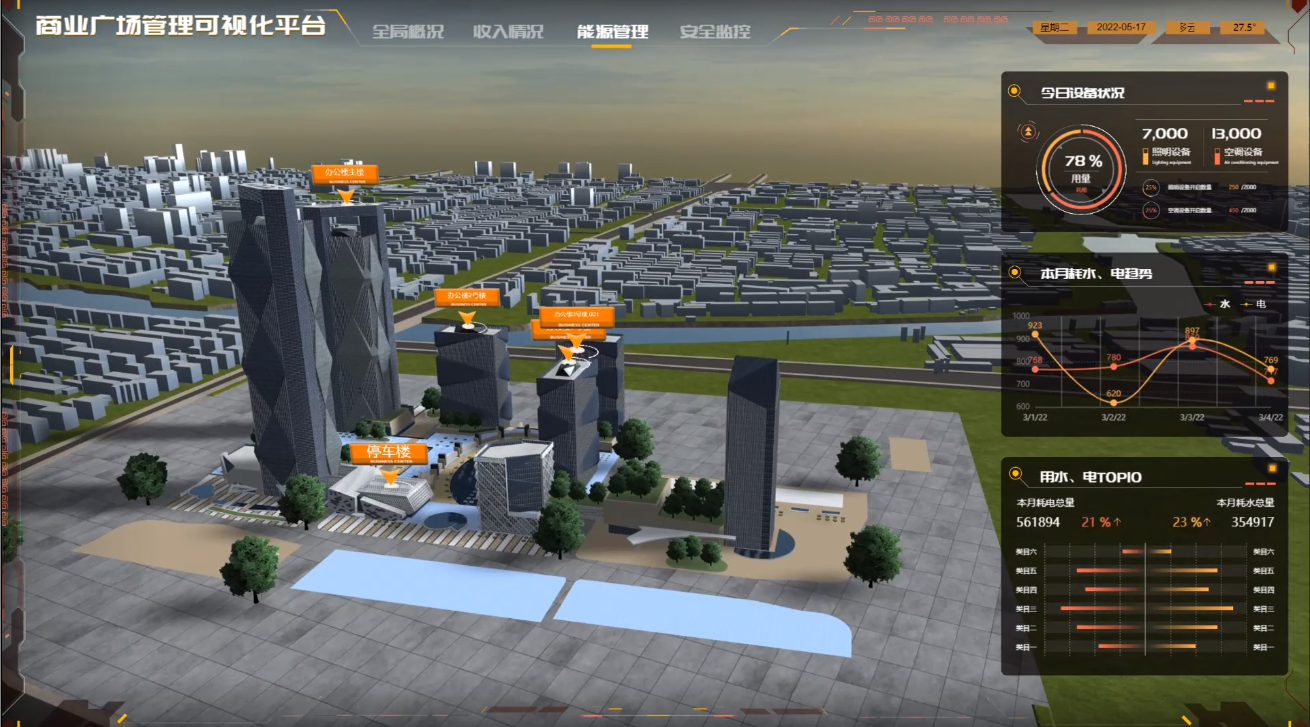
数字孪生与GIS:智慧城市的未来之路
数字孪生和地理信息系统(GIS)是两个在现代科技中崭露头角的概念,它们的融合为智慧城市项目带来了革命性的机会。本文将解释数字孪生为何需要融合GIS,并以智慧城市项目为例进行说明。 数字孪生是一种虚拟模型,它精确地…...

nas汇编程序的调试排错方法
nas汇编程序的调试排错方法: 1、查找是哪一步错了 2、查看对应的*.lst文件,本例中是"asmhead.lst" 3、根据*.lst文件的[ERROR #002]提示查看源码,改错。 4、重新运行编译,OK 1、查找是哪一步错了: nask.ex…...

【网络安全带你练爬虫-100练】第21练:批量获取文件夹中文件名
目录 一、目标1:使用python爬取指定文件夹中的文件名 二、目标2:在文件夹指定目录打开命令行 一、目标1:使用python爬取指定文件夹中的文件名 方法一:使用os模块 将/path/to/folder替换为实际的文件夹路径。os.listdir()函数用…...
Unittest自动化测试框架vs Pytest自动化测试框架
引言 前面一篇文章Python单元测试框架介绍已经介绍了python单元测试框架,大家平时经常使用的是unittest,因为它比较基础,并且可以进行二次开发,如果你的开发水平很高,集成开发自动化测试平台也是可以的。而这篇文章…...

PHP8的数组-PHP8知识详解
今天开始学习数组, 本文主要讲了三点:什么是数组、php8中数组的改进、数组函数。 一、什么是数组 在PHP8中,数组是非常重要的数据类型。相对于其他的数据类型,数组更像一种结构,而这种结构可以储存一系列数值。 数组…...

数据仓库_维度表的两大分类
最近看一篇文章对维度表进行了分类,记录一下。 维度表主要分为两类高基数维度表和低基数维度表。 高基数维度数据 一般是用户资料表、商品资料表类似的资料表。数据量可能是千万级或者上亿级别。 低基数维度数据 一般是配置表,比如枚举值对应的中文含…...

4、DVWA——文件包含
文章目录 一、文件包含概述二、low2.1 源码分析2.2 通关分析 三、medium3.1 源码分析3.2 通关思路 四、high4.1 源码分析4.2 通关思路 五、impossible 一、文件包含概述 文件包含是指当服务器开启allow_url_include选项时,就可以通过php的某些特性函数(i…...

产品经理如何进行需求管理
产品经理在进行需求管理时,可以遵循以下步骤: 1. 确定需求目标:明确产品的愿景和目标,确定需求管理的方向和重点。 2. 收集需求:与利益相关者(包括用户、业务部门、技术团队等)沟通,…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...
