【高阶数据结构】AVL树 {概念及实现;节点的定义;插入并调整平衡因子;旋转操作:左单旋,右单旋,左右双旋,右左双旋;AVL树的验证及性能分析}
AVL树
一、AVL树的概念
-
二叉搜索树虽可以缩短查找的效率,但如果数据有序或接近有序二叉搜索树将退化为单支树,查找元素相当于在顺序表中搜索元素,效率低下。因此,两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年发明了一种解决上述问题的方法:
-
AVL树:又被称为高度平衡搜索二叉树,当向二叉搜索树中插入新结点后,如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整),即可降低树的高度,从而减少平均搜索长度。
一棵AVL树或者是空树,或者是具有以下性质的二叉搜索树:
- 左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)
- 它的左右子树都是AVL树

如果一棵二叉搜索树是高度平衡的,它就是AVL树。如果它有n个结点,其高度可保持在log_2 n,搜索时间复杂度O(log_2 n)。
二、AVL树节点的定义
template <class K, class V>
struct AVLTreeNode{ AVLTreeNode<K,V> *_left; //指向左节点的指针 AVLTreeNode<K,V> *_right; //指向右节点的指针 AVLTreeNode<K,V> *_parent; //指向父节点的指针 pair<K,V> _kv; //存储元素键值对 int _bf; //平衡因子balance factor AVLTreeNode(const pair<K,V> &kv) :_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _bf(0) {}
};
三、AVL树的插入
AVL树就是在二叉搜索树的基础上引入了平衡因子,因此AVL树也可以看成是二叉搜索树。那么AVL树的插入过程可以分为三步:
- 按照二叉搜索树的方式插入新节点
- 调整节点的平衡因子
- 如果节点所在的二叉树不再平衡,通过旋转恢复平衡。

template <class K, class V>
bool AVLTree<K,V>::Insert(const pair<K,V> &kv)
{//1.按照二叉搜索树的方式插入新节点if(_root == nullptr){_root = new Node(kv);return true;}Node *cur = _root;Node *parent = nullptr; //cur要向下一直遍历到null,所以要记录父节点的指针while(cur != nullptr){if(kv.first > cur->_kv.first) {parent = cur;cur = cur->_right;}else if(kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);if(kv.first > parent->_kv.first){ parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent; //不要忘了修改父节点指针//2.调整节点的平衡因子while(parent!=nullptr) //只影响插入节点的所有祖先节点的平衡因子,parent不断向上一直遍历到根节点{//更新父节点的平衡因子//平衡因子=右树的高度-左树的高度if(cur == parent->_right){++parent->_bf; //插入右节点,bf++; }else{--parent->_bf; //插入左节点,bf--;}//更新后检测双亲的平衡因子if(parent->_bf == 0){//由1/-1更新为0,说明以父节点为根的二叉树高度不变,无需继续向上调整。 break; }else if(abs(parent->_bf) == 1){//由0更新为1/-1,说明以父节点为根的二叉树高度增加了一层,需要继续向上调整。 parent = parent->_parent;cur = cur->_parent;}else if(abs(parent->_bf) == 2){//3.更新后为2/-2,说明parent所在的子树已经不平衡了,需要通过旋转恢复平衡。//......//下面的内容会有讲解↓↓↓}else{//除非代码有错,否则不可能有其他情况。assert(false);}}return true;
}
四、AVL树的旋转
如果在一棵原本是平衡的AVL树中插入一个新节点,可能造成不平衡,此时必须调整树的结构,使之平衡化。根据节点插入位置的不同,AVL树的旋转分为四种:
4.1 左单旋
新节点插入较高右子树的右侧—右右:左单旋
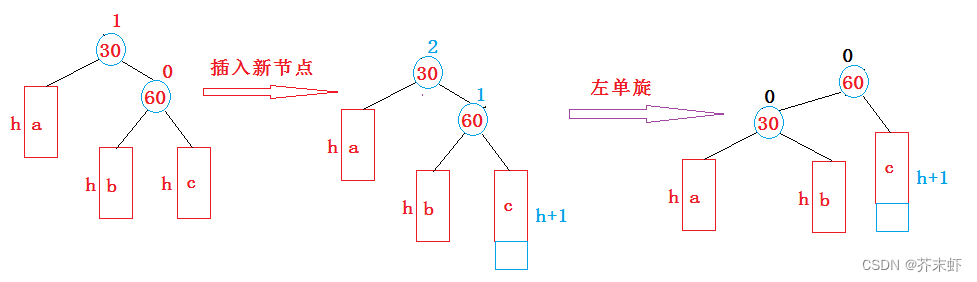
解释:
- 上图在插入前,AVL树是平衡的。a,b,c是高度为h的AVL子树(h>=0)。新节点插入到60的右子树c使c树增加了一层,最终导致以30为根的二叉树不平衡。
- 要让30平衡,就需要将30向左旋转,将60提上去。让30的左子树增加一层,右子树减少一层。也就是让30做60的左子树。
- 如果60有左子树b,b树的根一定大于30小于60,刚好做30的右子树。旋转完成后,更新节点的平衡因子即可。
- 在旋转过程中,有以下几种情况需要考虑:
- 60节点的左子树b可能存在,也可能为空。
- 30可能是根节点,也可能是子树
- 如果是根节点,旋转完成后,要更新根节点指针_root。
- 如果是子树,可能是某个节点的左子树,也可能是右子树。要更新父节点的指针。
template <class K, class V>
void AVLTree<K,V>::RotateL(Node *parent){ //parent对应30Node *subR = parent->_right; //subR对应60Node *subRL = subR->_left; //subRL对应b树的根Node *ppNode = parent->_parent; //记录30的父节点,便于旋转后进行连接。//30和b树进行连接parent->_right = subRL; if(subRL != nullptr) //b树可能为空{subRL->_parent = parent;}//30和60重新连接subR->_left = parent;parent->_parent = subR;//60和30的父节点进行连接//如果30是根节点,更新根节点指针_root指向60//if(_root == parent)if(ppNode == nullptr){_root = subR;}else{//60和30的父节点进行连接,先要确定30是父节点的左子树还是右子树if(ppNode->_left == parent){ppNode->_left = subR;}else{ ppNode->_right = subR;}}subR->_parent = ppNode;//更新平衡因子,进过旋转60和30的平衡因子变为0subR->_bf = parent->_bf = 0;
}
4.2 右单旋
新节点插入较高左子树的左侧—左左:右单旋
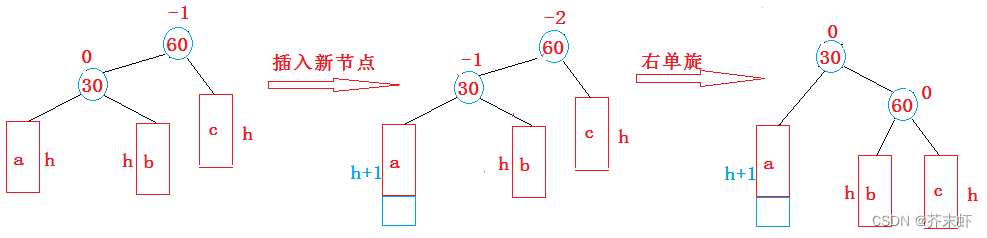
详细解释参考左单旋。
template <class K, class V>
void AVLTree<K,V>::RotateR(Node *parent){Node *subL = parent->_left;Node *subLR = subL->_right;Node *ppNode = parent->_parent;parent->_parent = subL;subL->_right = parent; parent->_left = subLR;if(subLR != nullptr)subLR->_parent = parent;//if(_root == parent)if(ppNode == nullptr){_root = subL;}else{if(ppNode->_left == parent){ppNode->_left = subL;}else{ppNode->_right = subL;}}subL->_parent = ppNode;subL->_bf = parent->_bf = 0;
}
旋转的作用:1. 平衡二叉树 2. 降低二叉树高度(恢复到插入之前的高度h+2)
4.3 左右双旋
新节点插入较高左子树的右侧—左右:先左单旋再右单旋

将双旋变成单旋后再旋转,即:先对30进行左单旋,然后再对90进行右单旋,旋转完成后再考虑平衡因子的更新。
左右双旋又能细分为3种情况:
- a,b,c,d是空树60是新增,引发双旋。
- 在b树插入新增,引发双旋。
- 在c树插入新增,引发双旋。
三种情况的双旋过程不变,只是平衡因子的更新需要分别处理:
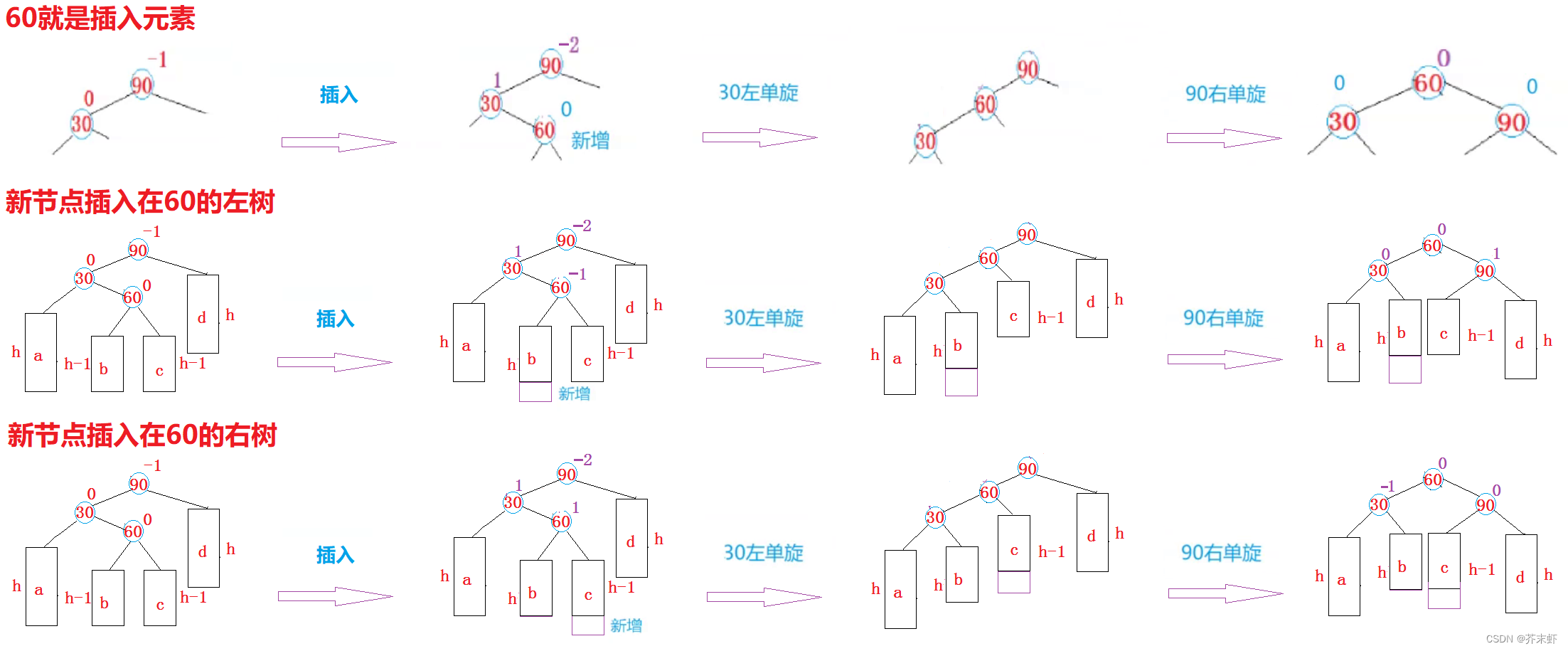
双旋的关键在于更新平衡因子,30,60,90三个节点的平衡因子都在两次单旋过程中被错误的置为0(因为并没要满足单旋的条件)。要根据以上三种不同的情况重新调整三个节点的平衡因子。如何区分三种不同的情况?根据旋转之前60的平衡因子确认。
template <class K, class V>
void AVLTree<K,V>::RotateLR(Node *parent){ //parent对应90Node *subL = parent->_left; //subL对应30Node *subLR = subL->_right; //subLR对应60int bf = subLR->_bf; //记录旋转之前60的平衡因子RotateL(subL); //30左单旋RotateR(parent); //90右单旋//更新平衡因子subLR->_bf = 0; //60的平衡因子一定为0 switch(bf) //根据旋转之前60的平衡因子确认属于那种情况{case 1:subL->_bf = -1;parent->_bf = 0;break;case -1:subL->_bf = 0;parent->_bf = 1;break;case 0:subL->_bf = 0;parent->_bf = 0;break;default://除非代码有错,否则不可能有其他情况。assert(false);break;}
}
双旋最终的结果是将60作为二叉树的根,60的左右子树分别作了30和90的右左子树。30和90作了60的左右子树。
4.4 右左双旋
新节点插入较高右子树的左侧—右左:先右单旋再左单旋

详细解释参考左右双旋。
template <class K, class V>
void AVLTree<K,V>::RotateRL(Node *parent){Node *subR = parent->_right;Node *subRL = subR->_left;int bf = subRL->_bf;RotateR(subR);RotateL(parent); //更新平衡因子 subRL->_bf = 0;switch(bf){case 1:subR->_bf = 0;parent->_bf = -1;break;case -1:subR->_bf = 1;parent->_bf = 0;break;case 0:subR->_bf = 0;parent->_bf = 0;break;default://除非代码有错,否则不可能有其他情况。assert(false);break;}
}
双旋最终的结果是将60作为二叉树的根,60的左右子树分别作了30和90的右左子树。30和90作了60的左右子树。
4.5 分情况旋转
else if(abs(parent->_bf) == 2){ //3.更新后为2/-2,说明parent所在的子树已经不平衡了,需要通过旋转恢复平衡。if(parent->_bf == 2 && cur->_bf == 1) //右右,左单旋{RotateL(parent);}else if(parent->_bf == 2 && cur->_bf == -1) //右左,右左双旋{RotateRL(parent);}else if(parent->_bf == -2 && cur->_bf == -1) //左左,右单旋{RotateR(parent); }else if(parent->_bf == -2 && cur->_bf == 1) //左右,左右双旋{RotateLR(parent);}else{//除非代码有错,否则不可能有其他情况。assert(false);}break; //注意:旋转完成后,原parent为根的子树个高度降低,已经平衡,不需要再向上更新。}
总结:
假如以parent为根的子树不平衡,即parent的平衡因子为2或者-2,分以下情况考虑:
-
parent的平衡因子为2,说明parent的右子树高,设parent的右子树的根为subR
-
当subR的平衡因子为1时(右右),执行左单旋
-
当subR的平衡因子为-1时(右左),执行右左双旋
-
-
parent的平衡因子为-2,说明parent的左子树高,设parent的左子树的根为subL
-
当subL的平衡因子为-1是(左左),执行右单旋
-
当subL的平衡因子为1时(左右),执行左右双旋
-
经过旋转后可以直接break;因为经过旋转,插入元素前后子树的高度未发生变化都是h+2,不需要再调整上层节点的平衡因子。一次插入最多一次旋转。
所以,AVL树插入元素的时间复杂度:找插入位置O(log_2N) + 更新平衡因子O(log_2N) + 旋转O(1) = O(log_2N)。
五、AVL树的验证
AVL树是在二叉搜索树的基础上加入了平衡性的限制,因此要验证AVL树,可以分两步:
-
验证其为二叉搜索树
如果中序遍历可得到一个有序的序列,就说明为二叉搜索树 -
验证其为平衡树
-
每个节点子树高度差的绝对值不超过1
-
节点的平衡因子是否计算正确
template <class K, class V> bool AVLTree<K,V>::_Isbalance(Node *root){if(root == nullptr) return true; //注意,空树也是AVL树int lh = _Height(root->_left); //_Height返回二叉树的高度int rh = _Height(root->_right);int diff = rh-lh; //计算得到平衡因子 if(diff != root->_bf){cout << "Key: " << root->_kv.first << "bf: " << root->_bf << " 平衡因子异常" << endl;return false;}return abs(diff) < 2 && _Isbalance(root->_left) && _Isbalance(root->_right); }
-
测试用例
//插入一两组序列测试 void Test1(){//int arr[] = {16, 3, 7, 11, 9, 26, 18, 14, 15};int arr[] = {1,2,3,4,5,6,7,8,9,10};AVLTree<int, int> avl;for(auto e : arr){avl.Insert(make_pair(e, e)); }avl.Inorder();cout << "Isbalance: " << avl.Isbalance() << endl; }//插入10000个随机值测试 void Test2(){srand(time(NULL));AVLTree<int, int> avl;const int N = 10000;for(int i = 0; i<N; ++i){int x = rand();avl.Insert(make_pair(x, i));}cout << "Isbalance: " << avl.Isbalance() << endl; }
六、AVL树的删除(了解)
AVL树节点的删除步骤如下:
- 在AVL树中找到要删除的节点。
- 如果要删除的节点是叶子节点,直接删除即可。
- 如果要删除的节点只有一个子节点,先使前驱节点指向该节点的子节点,然后删除该节点。
- 如果要删除的节点有两个子节点,需要找到该节点的替换节点(即该节点右子树中最小的节点或左子树中最大的节点),然后交换与替换节点的值,最后删除替换节点。
- 在删除节点后,需要更新从该节点到根节点路径上所有节点的平衡因子,并进行平衡调整,使得整棵树重新满足AVL树的性质。
删除操作的平衡调整方法和AVL树的插入操作相似,但在实现时需要注意一些细节上的差异。需要注意的是,删除操作可能会导致多个节点的平衡因子发生变化,因此需要一直向上循环更新和平衡调整,直到根节点。具体实现大家可以参考《算法导论》或《数据结构-用面向对象方法与C++描述》殷人昆版。
七、AVL树的性能
-
AVL树是一棵绝对平衡的二叉搜索树,其要求每个节点的左右子树高度差的绝对值都不超过1,这样可以保证查询时高效的时间复杂度,即
log_2 (N)。 -
但是如果要对AVL树做一些结构修改的操作,性能非常低下,比如:插入时要维护其绝对平衡,旋转的次数比较多;更差的是在删除时,有可能一直要让旋转持续到根的位置。
-
因此,如果需要一种查询高效且有序的数据结构,而且数据的个数为静态的(即不会改变),可以考虑AVL树。但一个结构经常修改,就不太适合。
相关文章:

【高阶数据结构】AVL树 {概念及实现;节点的定义;插入并调整平衡因子;旋转操作:左单旋,右单旋,左右双旋,右左双旋;AVL树的验证及性能分析}
AVL树 一、AVL树的概念 二叉搜索树虽可以缩短查找的效率,但如果数据有序或接近有序二叉搜索树将退化为单支树,查找元素相当于在顺序表中搜索元素,效率低下。因此,两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年发明…...
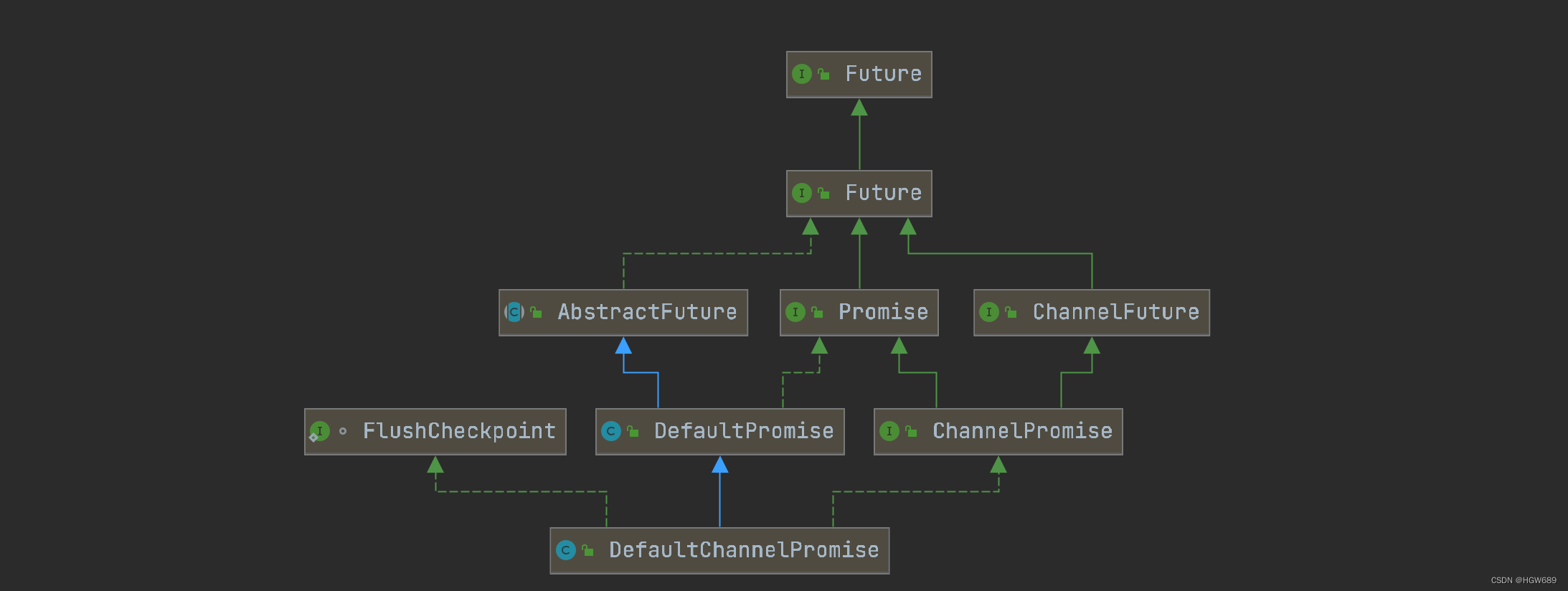
Netty—FuturePromise
Netty—Future&Promise 一、JDK原生 Future二、Netty包下的 Future三、Promise1、使用Promise同步获取结果2、使用Promise异步获取结果.3、使用Promise同步获取异常 - sync & get4、使用Promise同步获取异常 - await5、使用Promise异步获取异常 在异步处理时࿰…...

固定资产卡片乱怎么管理
固定资产卡片是记录公司固定资产信息的重要工具,如果管理不善,容易造成卡片混乱、数据错误等问题。 为了避免这种情况的发生,可以采取以下措施: 建立完善的资产管理制度,明确固定资产的分类、标准和使用情况&#x…...

AutoHotkey(AHK)脚本,自动截图当前屏幕并发送给微信窗口
前提先安装好 AutoHotkey ,本脚本依赖AutoHotkey 环境 首先 ,设置微信的快捷键 执行代码如下: Loop {SendInput, {Alt down}s{Alt up}Sleep, 2000 ; 等待2秒; 双击鼠标左键Click, 2Sleep, 1000 ; 等待1秒SendInput, {Alt down}a{Alt up}Sl…...

Golang - go build打包文件
Go编译打包文件 1、简单打包 程序 main1.go: package mainimport "fmt"func main() {fmt.Println("Hello World!") } 打包: # 在linux服务上执行下面的3个命令 # linux平台,生成main1可执行程序 CGO_ENABLED0 GOOSlinux GOARCHam…...

Java的归并排序
不爱生姜不吃醋⭐️⭐️⭐️ 如果本文有什么错误的话欢迎在评论区中指正 与其明天开始,不如现在行动! 文章目录 🌴前言🌴一.归并排序1.概念2.时间复杂度3.代码实现 🌴二、小和问题1.概念2.举例3.代码实现 🌴…...
)
B. The Walkway Codeforces Round 893 (Div. 2)
Problem - B - Codeforces 题目大意:小明在数轴上要从1走到n,其中某些坐标上有一些饼干店,共m个,小明身上也有无限多的饼干,它首先一定会在1的位置吃一个饼干,在每个饼干店的位置会吃一个,在前…...

第四篇 DirectShow 采集调用结构关系
第一篇: DirectShow视频采集_会头痛的可达鸭的博客-CSDN博客 一、GraphBuilder 1、IFilterGraph2、IGraphBuilder、ICaptureGraphBuiler2 (1)、CLSID IFilterGraph CLSID_FilterGraphIFilterGraph2 CLSID_CaptureGraphBuilderIGraphBuilder CL…...

2605. 从两个数字数组里生成最小数字
文章目录 Tag题目来源题目解读解题思路方法一:枚举比较法方法二:集合的位运算表示法 写在最后 Tag 【贪心】【位运算】【数组】 题目来源 2605. 从两个数字数组里生成最小数字 题目解读 给定两个各自只包含数字 1 到 9 的两个数组,每个数组…...
服务器发送事件Server-sent events详解与示例
Server-sent events 服务端进行数据推送除了WebSocket之外,还可以使用Server-Send-Event方案。 与 WebSocket不同的是,服务器发送事件是单向的。数据消息只能从服务端到发送到客户端(如用户的浏览器)。这使其成为不需要从客户端…...
SOLIDWORKS 多实体的建模方式
SOLIDWORKS多实体是SOLIDWORKS中一个非常有用的功能。在SOLIDWORKS中,对于模型的设定通常被大家所熟知的有以下几种类型:零件、装配体以及工程图。 其实还有一种划分,就是多实体。严格意义上来说,多实体既不属于零件也不属于装配体…...

NSSCTF web 刷题记录1
文章目录 前言题目[GXYCTF 2019]禁止套娃方法一方法二 [NCTF 2019]Fake XML cookbook[NSSRound#7 Team]ec_RCE[NCTF 2018]Flask PLUS 前言 今天是2023.9.3,大二开学前的最后一天。老实说ctf的功力还是不太够做的题目太少,新学期新气象。不可急于求成&am…...
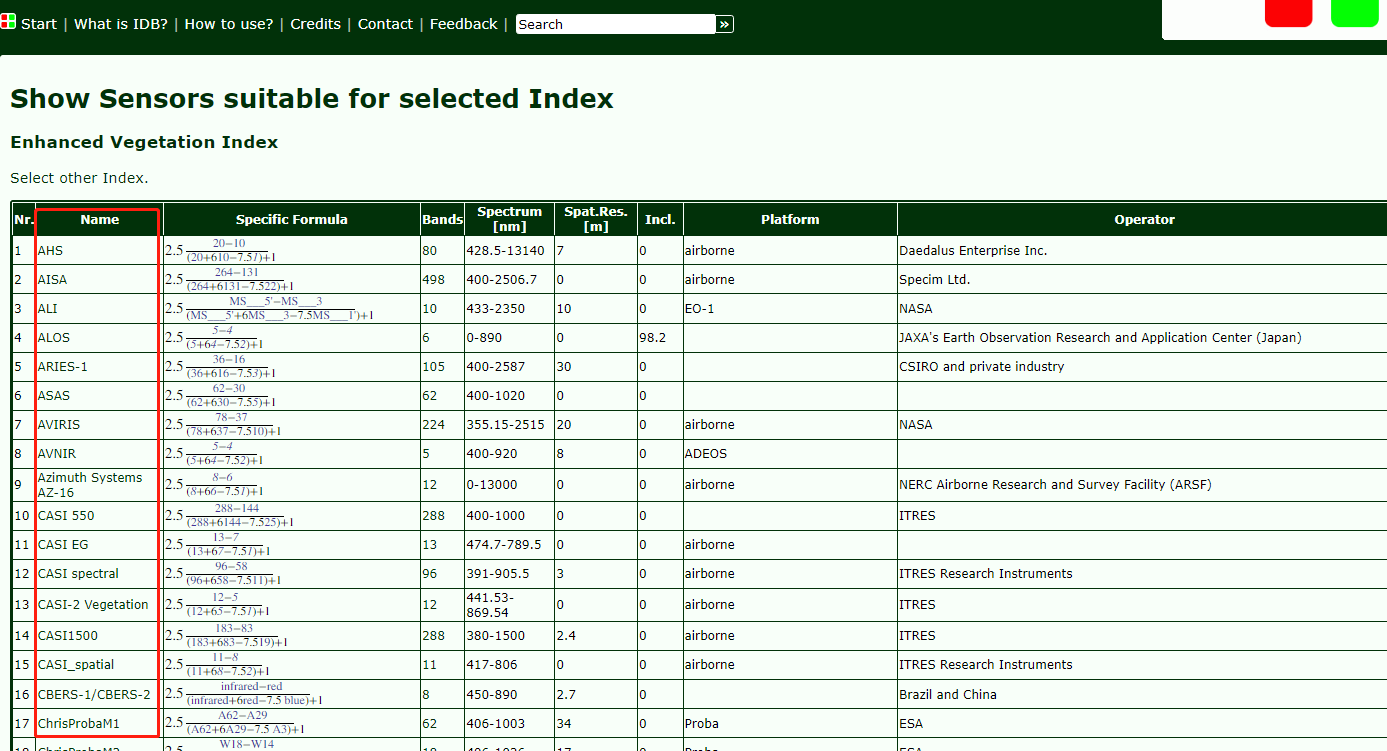
遥感指数数据库
目前遥感指数多种多样,那怎么针对不同的应用领域选择合适的植被指数?不同卫星又有哪些可以反演的指数? Henrich等人开发了Index Database(网址:https://www.indexdatabase.de/),总结了目前主流的遥感指数,…...
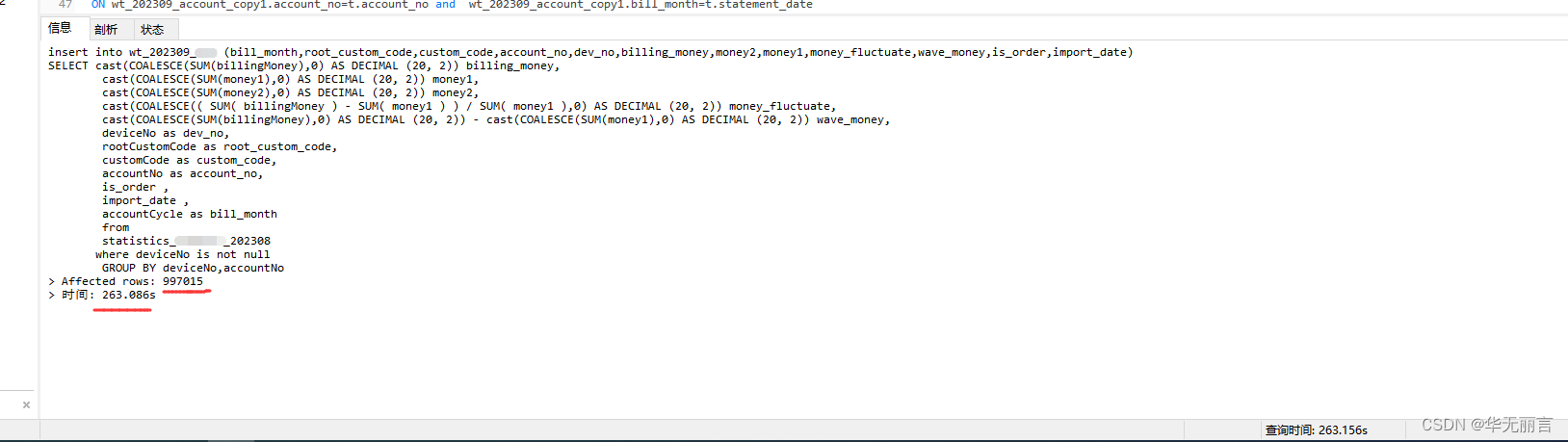
如何让insert程序速度快,可以试试联合SQL(insert 和 select 一起使用)?
查询添加可选择SQL执行,速度远超程序执行 insert 和 select案例 insert into 表1(列1,列2,列3,...) select 列1,列2,列3,...from表2(GROUP BY 列)116511 条数据 耗时45秒, 如果是程序查询然后再insert,则需要30分钟左右!&#x…...
IP地址、网关、网络/主机号、子网掩码关系
一、IP地址 IP地址组成 IP地址分为两个部分:网络号和主机号 (1)网络号:标识网段,保证相互连接的两个网段具有不同的标识。 (2)主机号:标识主机,同一网段内,主机之间具有相同的网…...

使用skvideo.io.vread读取avi视频,报错“No way to determine width or height from video...”
问题描述: 一开始安装sk-video,在使用skvideo.io.vread读取avi视频,报错“No way to determine width or height from video. Need -s in inputdict. Consult documentation on I/O.” 解决方案: 1. 卸载sk-video pip uninsta…...
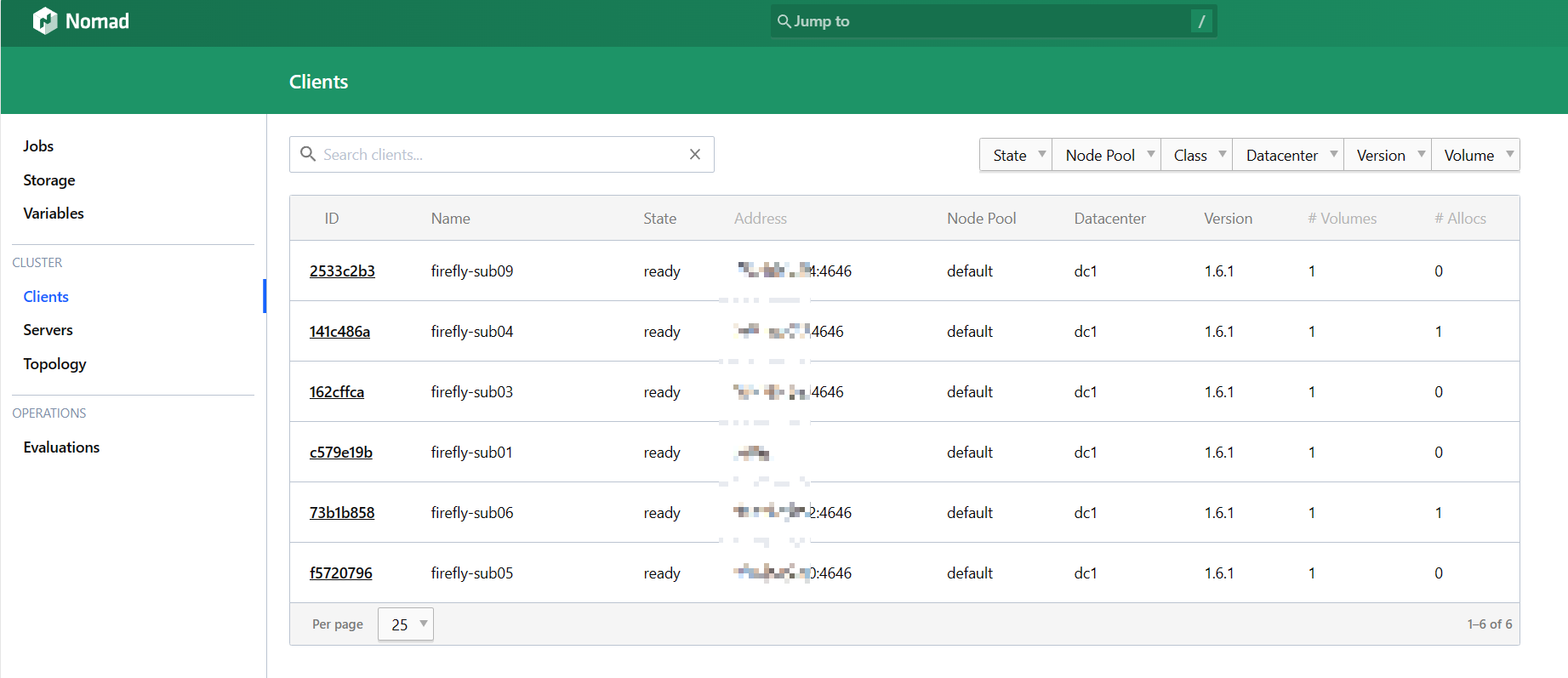
Nomad 系列-安装
系列文章 Nomad 系列文章 Nomad 简介 开新坑!近期算是把自己的家庭实验室环境初步搞好了,终于可以开始进入正题研究了。 首先开始的是 HashiCorp Nomad 系列,欢迎阅读。 关于 Nomad 的简介,之前在 大规模 IoT 边缘容器集群管…...
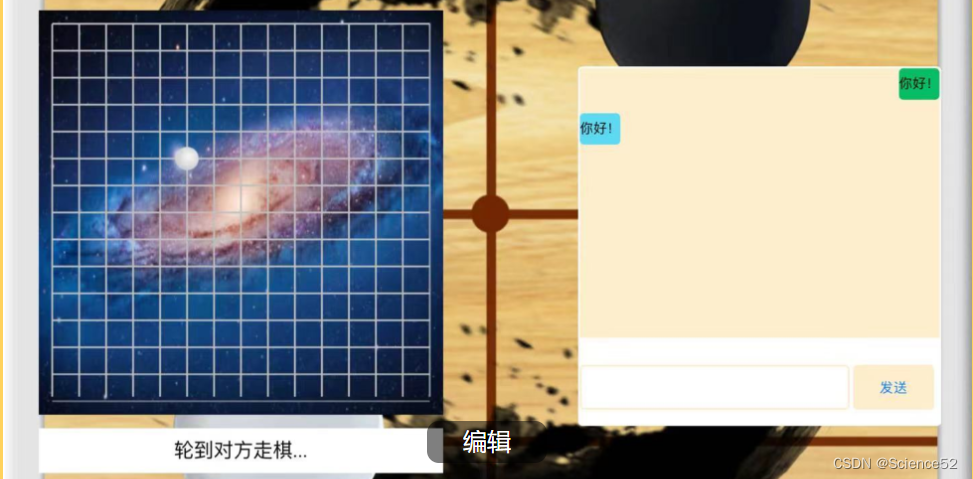
网络版五子棋C++实现
目录 1.项目介绍 2.开发环境 3.核心技术 4.环境搭建 5.WebSocketpp介绍 5.1WebSocketpp是什么 5.2为什么使用WebSocketpp 5.3原理解析: 5.4WebSocketpp主要特性 6.WebSocketpp使用 7.JsonCpp使用 8.MySQL API 9.项目模块设计以及流程图 10.封装日志宏…...

项目招标投标公众号小程序开源版开发
项目招标投标公众号小程序开源版开发 以下是一个招标投标公众号小程序的功能列表: 用户注册与登录:用户可以注册账号并登录公众号小程序。项目发布:用户可以发布招标项目的详细信息,包括项目名称、招标单位、项目描述、招标要求…...
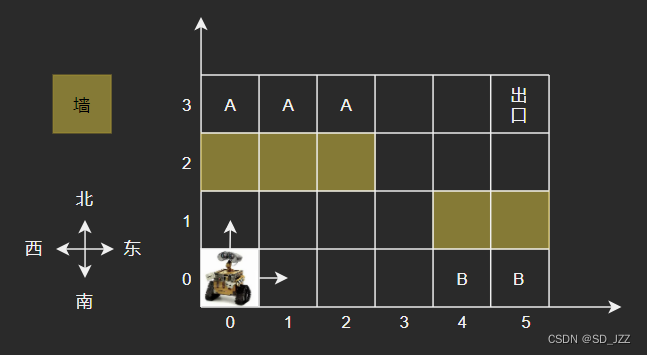
华为OD机试-机器人走迷宫
题目描述 机器人走一个迷宫,给出迷宫的x和y(x*y的迷宫)并且迷宫中有障碍物,输入k表示障碍物有k个,并且会将障碍物的坐标挨个输入. 机器人从0,0的位置走到x,y的位置并且只能向x,y增加的方向走,不能回退. 如代码类注释展示的样子,#表示可以走的方格,0代表障碍,机器人从0,0的位置…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...

node.js的初步学习
那什么是node.js呢? 和JavaScript又是什么关系呢? node.js 提供了 JavaScript的运行环境。当JavaScript作为后端开发语言来说, 需要在node.js的环境上进行当JavaScript作为前端开发语言来说,需要在浏览器的环境上进行 Node.js 可…...

Django RBAC项目后端实战 - 03 DRF权限控制实现
项目背景 在上一篇文章中,我们完成了JWT认证系统的集成。本篇文章将实现基于Redis的RBAC权限控制系统,为系统提供细粒度的权限控制。 开发目标 实现基于Redis的权限缓存机制开发DRF权限控制类实现权限管理API配置权限白名单 前置配置 在开始开发权限…...
深入理解 C++ 左值右值、std::move 与函数重载中的参数传递
在 C 编程中,左值和右值的概念以及std::move的使用,常常让开发者感到困惑。特别是在函数重载场景下,如何合理利用这些特性来优化代码性能、确保语义正确,更是一个值得深入探讨的话题。 在开始之前,先提出几个问题&…...
