机器学习——聚类算法一
机器学习——聚类算法一
文章目录
- 前言
- 一、基于numpy实现聚类
- 二、K-Means聚类
- 2.1. 原理
- 2.2. 代码实现
- 2.3. 局限性
- 三、层次聚类
- 3.1. 原理
- 3.2. 代码实现
- 四、DBSCAN算法
- 4.1. 原理
- 4.2. 代码实现
- 五、区别与相同点
- 1. 区别:
- 2. 相同点:
- 总结
前言
在机器学习中,有多种聚类算法可以用于将数据集中的样本按照相似性进行分组。本文将介绍一些常见的聚类算法:
- K-Means聚类
- 层次聚类
- DBSCAN算法
一、基于numpy实现聚类
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from numpy.linalg import norm
import random
np.random.seed(42)
data = np.random.randn(100,2) #生成一个包含100个样本点的随机数据集,每个样本有2个特征
df = pd.DataFrame(data= data,columns=["x1","x2"])x1_min, x1_max, x2_min, x2_max = df.x1.min(), df.x1.max() ,df.x2.min(), df.x2.max()# 初始化两个质心
centroid_1 = np.array([random.uniform(x1_min, x1_max), random.uniform(x2_min, x2_max)])
centroid_2 = np.array([random.uniform(x1_min, x1_max), random.uniform(x2_min, x2_max)])data = df.values
#设置迭代次数为10
for i in range(10):clusters = []for point in data:centroid_1_dist = norm(centroid_1- point) #计算两点之间的距离centroid_2_dist = norm(centroid_2- point)cluster = 1if centroid_1_dist > centroid_2_dist:cluster = 2clusters.append(cluster)df["cluster"] = clusters#更换质心(即迭代聚类点)
centroid_1 = [round(df[df.cluster == 1].x1.mean(),3), round(df[df.cluster == 1].x2.mean(),3)]
centroid_2 = [round(df[df.cluster == 2].x1.mean(),3), round(df[df.cluster == 2].x2.mean(),3)]plt.scatter(x1, x2, c=df["cluster"])
plt.scatter(centroid_1,centroid_2, marker='x', color='red')
plt.show()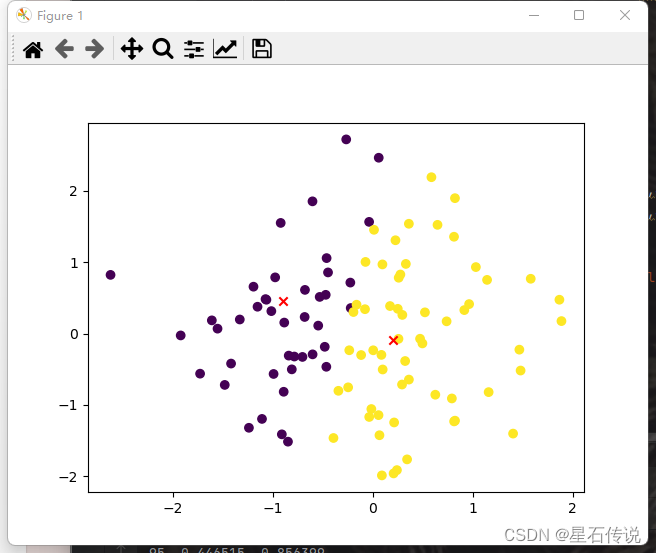
二、K-Means聚类
2.1. 原理
K-means 是一种迭代算法,它将数据集按照距离划分为 K 个簇(其中K是用户预先指定的簇的数量),每个簇代表一个聚类(聚类后同一类数据尽可能聚集到一起,不同类数据分离)。实现步骤如下:
- 随机初始化K个质心,每个质心代表一个簇
- 将每个样本点分配到距离其最近的质心所代表的簇。(如此就形成了K个簇)
- 更新每个簇的质心,(即计算每个簇中样本点的平均值)
- 重复步骤2和步骤3,直到质心的位置不再改变或达到预定的迭代次数。
2.2. 代码实现
- 导入数据集,以鸢尾花(iris)数据集为例:
from sklearn.datasets import load_iris
import pandas as pd# 加载数据集
iris = load_iris()#查看数据集信息
print(iris.keys())
dict_keys(['data', 'target', 'frame', 'target_names', 'DESCR', 'feature_names', 'filename', 'data_module'])#获取特征数据
data = iris["data"]# 获取标签数据
target = iris["target"]
print(pd.Series(target).unique())
[0 1 2]#查看分类名
print(iris["target_names"])
['setosa' 'versicolor' 'virginica']#整合到数据框
import pandas as pd
df = pd.DataFrame(data= iris["data"],columns= iris["feature_names"])
print(df.head())sepal length (cm) sepal width (cm) petal length (cm) petal width (cm)
0 5.1 3.5 1.4 0.2
1 4.9 3.0 1.4 0.2
2 4.7 3.2 1.3 0.2
3 4.6 3.1 1.5 0.2
4 5.0 3.6 1.4 0.2
- 确定初始化质点K的取值
肘部法则选择聚类数目:
该方法适用于K值相对较小的情况,随着聚类数目的增加,聚类误差(也称为SSE,Sum of Squared Errors)会逐渐减小。然而,当聚类数目达到一定阈值后,聚类误差的减小速度会变缓,形成一个类似手肘的曲线。这个手肘点对应的聚类数目就是肘部法则选择的合适聚类数目。
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
sse = []
# 设置聚类数目的范围
k_range = range(1, 10)
# 计算每个聚类数目对应的 SSE
for k in k_range:kmeans = KMeans(n_clusters=k,random_state = 42)kmeans.fit(df)sse.append(kmeans.inertia_)# 绘制聚类数目与 SSE 之间的曲线图
plt.style.use("ggplot")
plt.plot(k_range, sse,"r-o")
plt.xlabel('Number of K')
plt.ylabel('SSE')
plt.title('Elbow Method')
plt.show()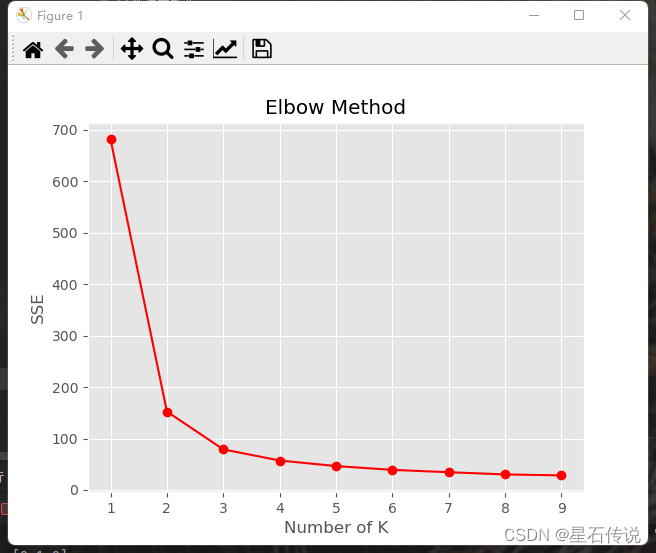
从图中可看出,当K=3时,该曲线变得比较平缓,则该点为肘部点。即最佳的聚类数目为K=3
- 从sklean中调用k-Means算法模型
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=3,max_iter= 400,random_state=42)
kmeans.fit(df)
print(kmeans.cluster_centers_)
y_kmeans = kmeans.labels_
df["y_kmeans"] = y_kmeans
- 可视化聚类结果
绘制平面图:
plt.scatter(df["sepal length (cm)"], df["sepal width (cm)"], c=df["y_kmeans"], cmap='viridis')
# 绘制聚类中心
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], c='red', marker='x', s=100)
plt.xlabel('Sepal Length')
plt.ylabel('Sepal Width')
plt.title('K-Means Clustering')
handles, labels = sc.legend_elements()
plt.legend(handles, labels)
plt.show()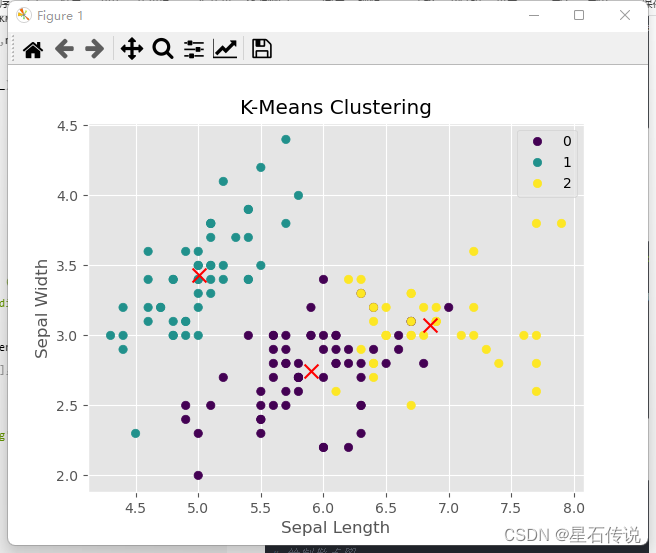
绘制三维图:
# 创建3D图形对象
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection='3d')
# 绘制散点图
sc = ax.scatter(df["sepal length (cm)"], df["sepal width (cm)"], df["petal length (cm)"], c=df["y_kmeans"], cmap='viridis')# 绘制聚类中心
ax.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], kmeans.cluster_centers_[:, 2], c='red', marker='x', s=100)ax.set_xlabel('Sepal Length')
ax.set_ylabel('Sepal Width')
ax.set_zlabel('Petal Length')
ax.set_title('K-Means Clustering')# 添加图例
handles, labels = sc.legend_elements()
ax.legend(handles, labels)plt.show()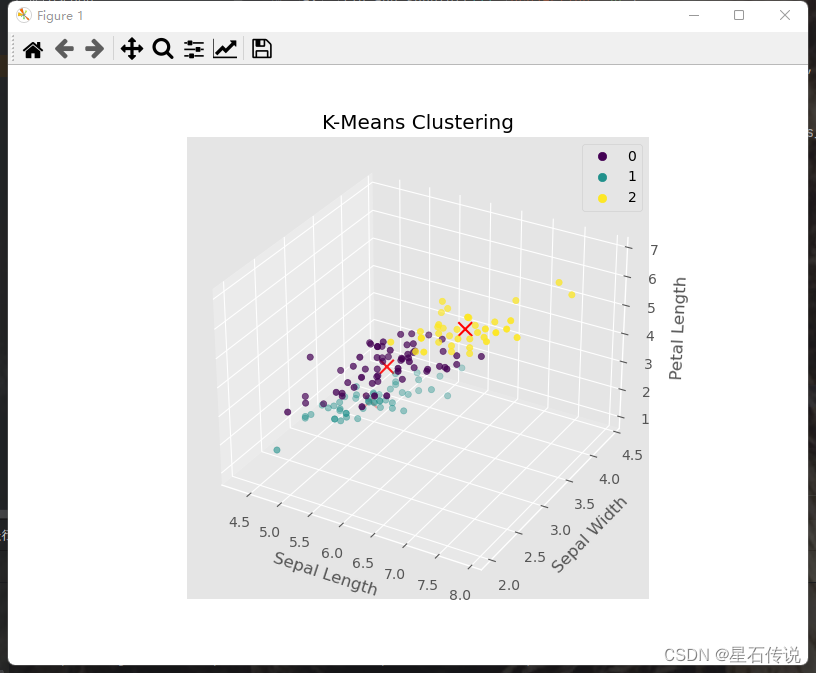
2.3. 局限性
k-Means算法通过距离来度量样本之间的相似性,因此对于非凸形状的聚类,算法可能无法正确地将样本划分到正确的聚类中。
k-Means算法对噪声和离群点敏感。这些异常值可能会影响到聚类结果,使得聚类变得不准确
需要事先指定聚类的数量k,而且对结果敏感。如果选择的聚类数量不合适,会导致聚类结果不准确或不理想。
比如这种情况:
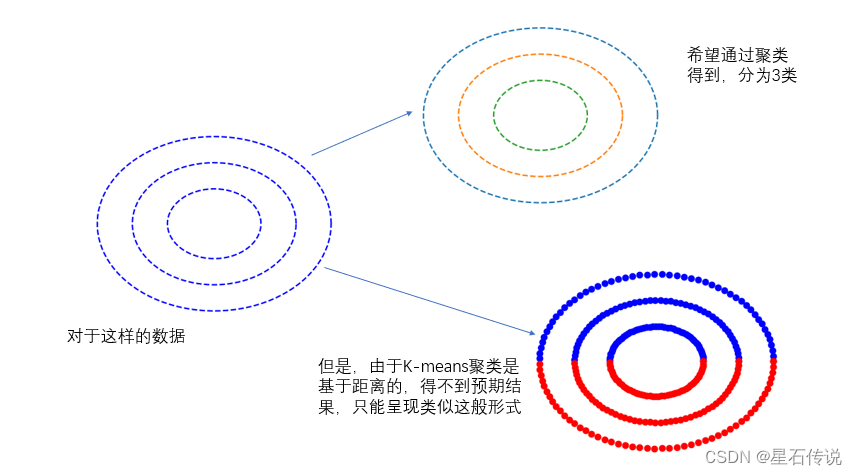
三、层次聚类
3.1. 原理
层次聚类(Agglomerative clustering)算法是一种基于树状结构的聚类方法,分为凝聚型和分裂型层次聚类。
分裂型层次聚类从整个数据集作为一个簇开始,然后逐步将簇分裂为更小的簇,直到达到预定的簇的数量或达到某个停止准则。
凝聚型层次聚类将数据集中的样本逐步合并为越来越大的簇。
即从N个簇开始(每个样本为一个簇),在每个步骤中合并两个最相似的簇,直到达到某个停止准则。
如图所示,从上(下)往下(上):
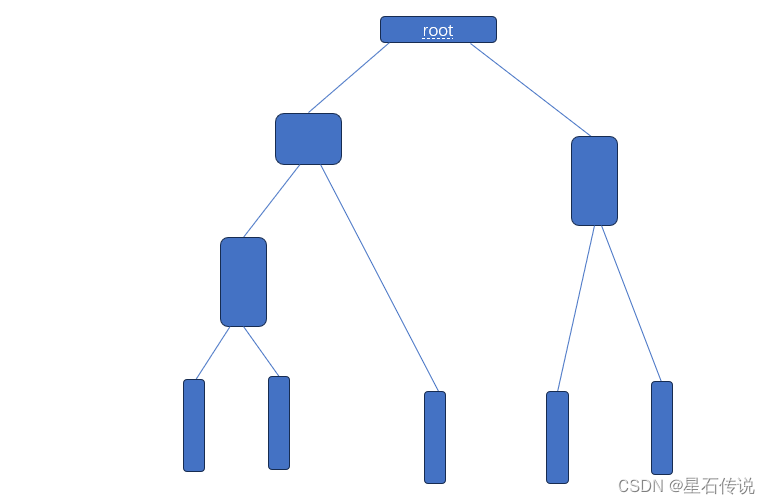
优点是可以直观地展示数据点之间的相似性关系,并且不一定要预先指定聚类簇的数量。
层次聚类的缺点是计算复杂度较高,且对数据的噪声和异常值比较敏感。
3.2. 代码实现
参数 linkage: 用于指定链接算法。
“ward” : 单链接,即两个簇的样本对之间距离的min
“complete”: 全链接,即两个簇的样本对之间距离的max
“average”: 均链接,即两个簇的样本对之间距离的mean
参数 affinity : 用于计算距离。
“euclidean”:使用欧几里德距离来计算数据点之间的距离(这是默认的距离度量方法)。
“manhattan”:使用曼哈顿距离来计算数据点之间的距离,它是两个点在所有维度上绝对值之和的总和。
“cosine”:使用余弦相似度来计算数据点之间的距离。
from sklearn.cluster import AgglomerativeClustering
cluster = AgglomerativeClustering()
print(cluster.fit_predict(df))cluster = AgglomerativeClustering(n_clusters= 3 ,linkage= "complete",affinity="manhattan")
cluster.fit(df)
df["cluster"] = cluster.labels_
print(cluster.labels_)# 创建3D图形对象
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection='3d')
plt.style.use("ggplot")for i in range(len(df["cluster"])):if df["cluster"][i] == 0:ax.scatter(df["sepal length (cm)"][i], df["sepal width (cm)"][i], df["petal length (cm)"][i],c = "red")elif df["cluster"][i] ==1:ax.scatter(df["sepal length (cm)"][i], df["sepal width (cm)"][i], df["petal length (cm)"][i],c = "blue")else:ax.scatter(df["sepal length (cm)"][i], df["sepal width (cm)"][i], df["petal length (cm)"][i],c = "yellow")ax.set_xlabel('Sepal Length')
ax.set_ylabel('Sepal Width')
ax.set_zlabel('Petal Length')
ax.set_title('Clustering')
plt.show()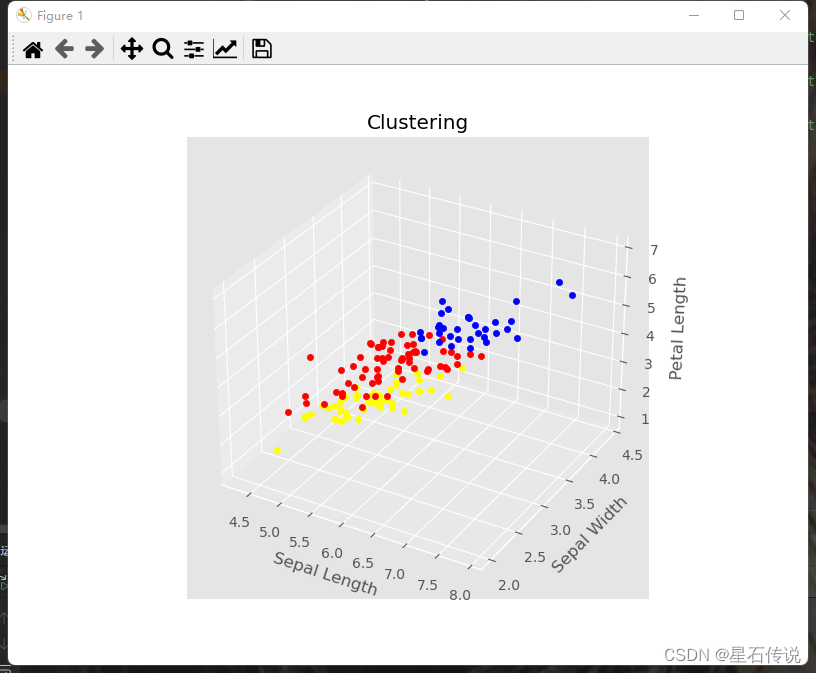
四、DBSCAN算法
4.1. 原理
DBSCAN是一种基于密度的聚类算法,它能够发现任意形状的聚类簇,并且能够识别出噪声点,它将样本划分为核心点、边界点和噪声点。算法的步骤如下:
-
随机选择一个未访问的样本点。根据设置的距离半径(eps),称在这一范围的区域为该样本实例的邻域
-
如果该样本点的邻域内样本数大于设定的阈值(min_samples),则将其标记为核心点,并将其邻域内的样本点加入到同一个簇中。
-
如果该样本点的邻域内样本数小于设定的阈值,则将其标记为边界点。
-
重复以上步骤,直到所有样本点都被访问。
-
最后,任何不是核心点,且邻域中没有实例样本的样本点都将被标记为噪声点
4.2. 代码实现
from sklearn.cluster import DBSCAN
cluster = DBSCAN(eps= 0.6 , min_samples= 10)
cluster.fit(df)
df["cluster"] = cluster.labels_
print(df)#-1代表噪声点
print(df["cluster"].value_counts())1 880 49
-1 13
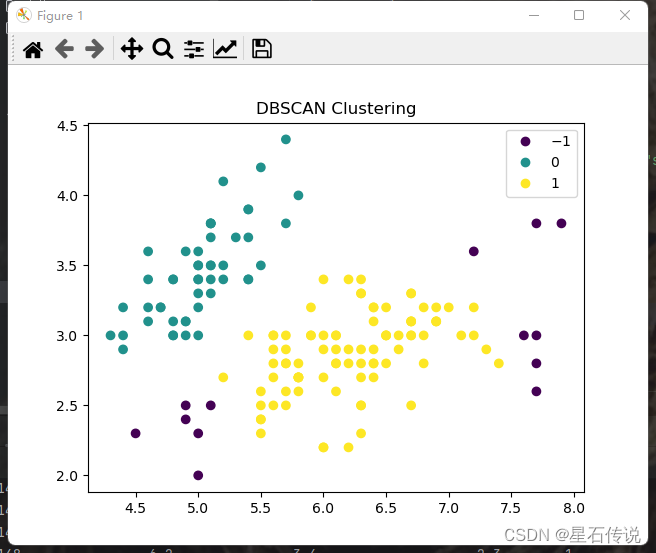
Name: cluster, dtype: int64sc = plt.scatter(df["sepal length (cm)"],df["sepal width (cm)"],c = df["cluster"])
plt.title('DBSCAN Clustering')
handles, labels = sc.legend_elements()
plt.legend(handles, labels)
plt.show()
from sklearn.cluster import DBSCAN
from sklearn.datasets import make_moons# 生成随机数据
X, y = make_moons(n_samples=200, noise=0.05)
print(X)dbscan = DBSCAN(eps=0.3, min_samples=5)
dbscan.fit(X)# 获取聚类标签
labels = dbscan.labels_#因为设置的noise很小,故没有噪声点
print(pd.Series(labels).value_counts())
0 100
1 100
dtype: int64# 绘制聚类结果
plt.scatter(X[:, 0], X[:, 1], c=labels)
plt.title('DBSCAN Clustering')
handles, labels = sc.legend_elements()
plt.legend(handles, labels)
plt.show()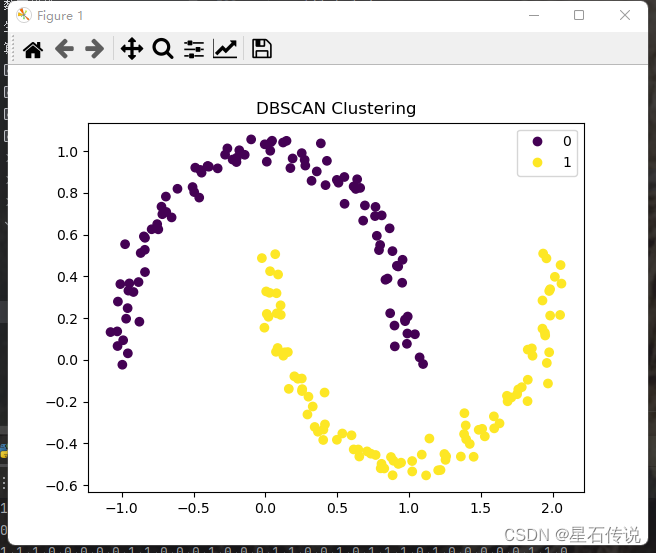
五、区别与相同点
1. 区别:
-
K-means是一种划分聚类算法,它将数据集划分为固定数量的簇(一定要预先指定簇的数量),而层次聚类(不一定要指定簇的数量)和DBSCAN算法(需要指定邻域半径和最小样本数),它们可以自动确定簇的数量。
-
K-means和层次聚类算法都假设簇具有相同的形状和大小,而DBSCAN算法可以发现任意形状和大小的簇。
-
K-means和层次聚类算法都对异常值敏感,而DBSCAN算法对异常值不敏感。(可去掉噪声点)
2. 相同点:
K-means、层次聚类和DBSCAN算法都是无监督学习算法中的聚类算法,它们不依赖于标签信息。
这些算法都使用距离或相似性度量来度量样本之间的相似性或距离。
总结
本文从最开始的自己实现聚类到后面的三个机器学习中聚类算法:( K-Means 、层次聚类、DBSCAN聚类)的学习,再到后面对这三个算法的比较与总结。加深了对聚类原理的了解。
我住长江头,君住长江尾;日日思君不见君
–2023-8-31 筑基篇
相关文章:

机器学习——聚类算法一
机器学习——聚类算法一 文章目录 前言一、基于numpy实现聚类二、K-Means聚类2.1. 原理2.2. 代码实现2.3. 局限性 三、层次聚类3.1. 原理3.2. 代码实现 四、DBSCAN算法4.1. 原理4.2. 代码实现 五、区别与相同点1. 区别:2. 相同点: 总结 前言 在机器学习…...
【2023研电赛】安谋科技企业命题三等奖作品: 短临天气预报AI云图分析系统
本文为2023年第十八届中国研究生电子设计竞赛安谋科技企业命题三等奖分享,参加极术社区的【有奖活动】分享2023研电赛作品扩大影响力,更有丰富电子礼品等你来领!,分享2023研电赛作品扩大影响力,更有丰富电子礼品等你来…...

The Sandbox 与韩国仁川市合作,打造身临其境的城市体验内容
简要概括 ● The Sandbox 与仁川市联手展示城市魅力,打造创新形象。 ● 本次合作包含多种多样的活动,如 NFT 捐赠活动和针对元宇宙创作者的培训计划。 我们非常高兴地宣布与仁川市合作,共同打造身临其境的城市体验。 双方合作的目的是在国…...
JVM之堆和方法区
目录 1.堆 1.1 堆的结构 1.1.1 新生代(Young Generation) 1.1.2 年老代(Old Generation) 1.1.3 永久代/元空间(Permanent Generation/Metaspace) 1.2 堆的内存溢出 1.3 堆内存诊断 1.3.1 jmap 1.3.2…...

Java 中的 IO 和 NIO
Java 中的 IO 和 NIO Java IO 介绍Java NIO(New IO)介绍windows 安装 ffmpeg完整示例参考文献 Java IO 介绍 Java IO(Input/Output)流是用于处理输入和输出数据的机制。它提供了一种标准化的方式来读取和写入数据,可以…...

Linux-crontab使用问题解决
添加定时进程 终端输入: crontab -e选择文本编辑方式,写入要运行的脚本,以及时间要求。 注意,如果有多个运行指令分两种情况: 1.多个运行指令之间没有耦合关系,分别独立,则可以直接分为两个…...
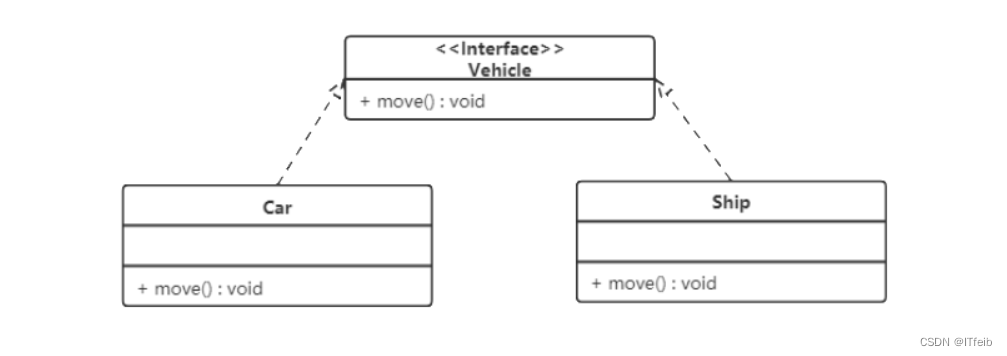
【设计模式】
文章目录 设计模式分类UML图类与类之间关系的表示方式 设计原则 设计模式分类 创建型模式 用于描述“怎样创建对象”,它的主要特点是“将对象的创建与使用分离”。单例、原型、工厂、抽象工厂、建造者等 5 种创建型模式。 结构型模式 用于描述如何将类或对象按某种…...

2023_Spark_实验四:SCALA基础
一、在IDEA中执行以下语句 或者用windows徽标R 输入cmd 进入命令提示符 输入scala直接进入编写界面 1、Scala的常用数据类型 注意:在Scala中,任何数据都是对象。例如: scala> 1 res0: Int 1scala> 1.toString res1: String 1scala…...

【深入解析spring cloud gateway】04 Global Filters
上一节学习了GatewayFilter。 回忆一下一个关键点: GateWayFilterFactory的本质就是:针对配置进行解析,为指定的路由,添加Filter,以便对请求报文进行处理。 一、原理分析 GlobalFilter又是啥?先看一下接口…...

c++搜索基础进阶
搜索算法基础 搜索算法是利用计算机的高性能来有目的的穷举一个问题的部分或所有的可能情况,从而求出问题的解的一种方法。搜索过程实际上是根据初始条件和扩展规则构造一棵解答树并寻找符合目标状态的节点的过程。 所有的搜索算法从其最终的算法实现上来看&#…...

管网水位监测的必要性
城市燃气、桥梁、供水、排水、热力、电力、电梯、通信、轨道交通、综合管廊、输油管线等,担负着城市的信息传递、能源输送、排涝减灾等重要任务,是维系城市正常运行、满足群众生产生活需要的重要基础设施,是城市的生命线。基础设施生命线就像…...

无涯教程-Android - 系统架构
Android操作系统是一堆软件组件,大致分为五个部分和四个主要层,如体系结构图中所示。 Linux内核 底层是Linux-Linux 3.6,带有大约115个补丁,这在设备硬件之间提供了一定程度的抽象,并且包含所有必需的硬件驱动程序&am…...

await接受成功的promise,失败的promise用try catch
在 JavaScript 中,await 关键字用于等待一个 Promise 对象的解决(fulfillment)。下面是一个示例: async function example() {try {const result await doSomethingAsync();console.log(result); // 如果 Promise 成功解决&…...
赞奇科技参与华为云828 B2B企业节,云工作站入选精选产品解决方案
8月27日,由华为云携手上万家伙伴共同发起的第二届 828 B2B 企业节拉开帷幕,围绕五大系列活动,为万千中小企业带来精细化商机对接。 聚焦行业数字化所需最优产品,举办超1000场供需对接会,遍及20多个省100多个城市&…...
Docker私有镜像仓库(Harbor)安装
Docker私有镜像仓库(Harbor)安装 1、什么是Harbor Harbor是类似与DockerHub 一样的镜像仓库。Harbor是由VMware公司开源的企业级的Docker Registry管理项目,它包括权限管理(RBAC)、LDAP、日志审核、管理界面、自我注册、镜像复制和中文支持等功能。Docker容器应用的…...
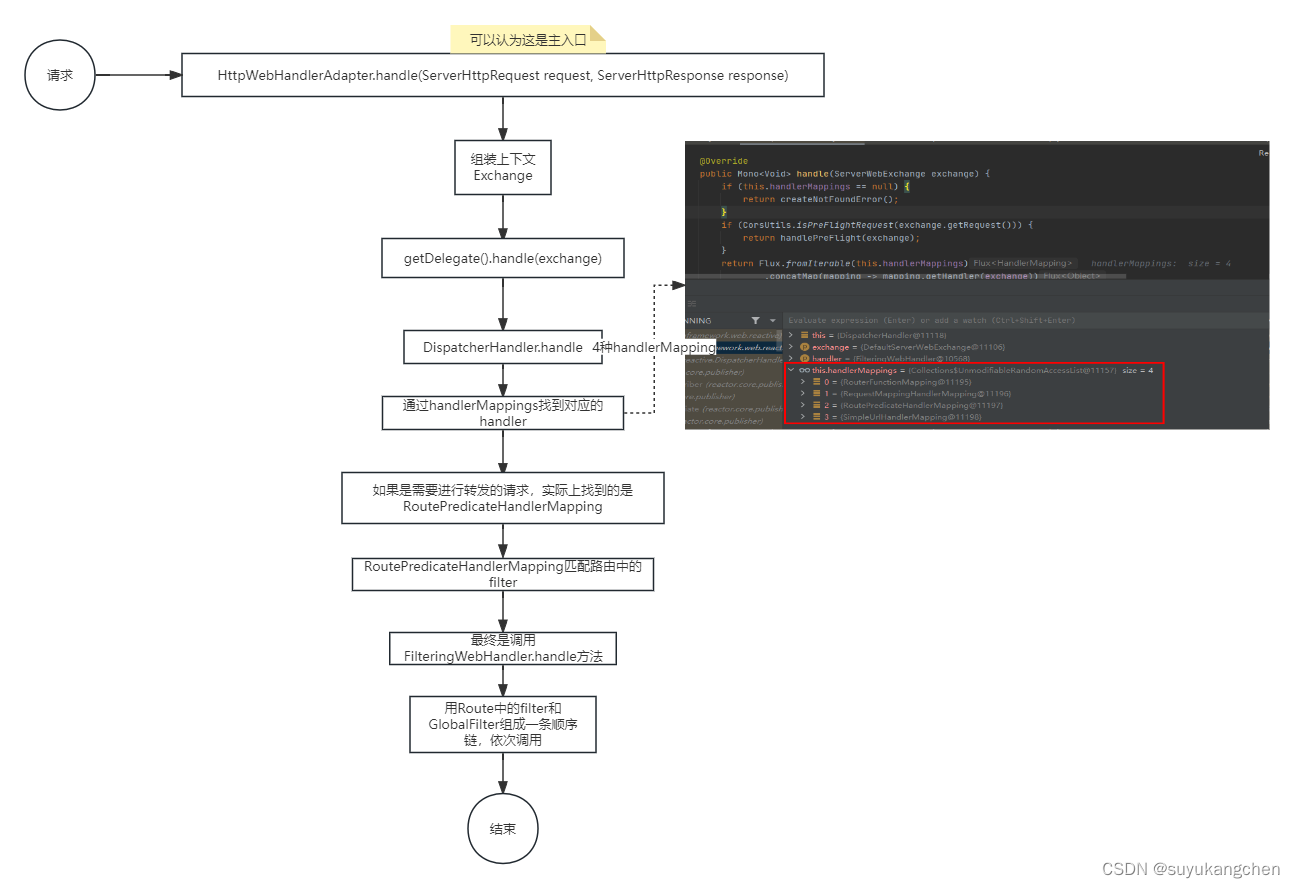
【深入解析spring cloud gateway】06 gateway源码简要分析
上一节做了一个很简单的示例,微服务通过注册到eureka上,然后网关通过服务发现访问到对应的微服务。本节将简单地对整个gateway请求转发过程做一个简单的分析。 一、核心流程 主要流程: Gateway Client向 Spring Cloud Gateway 发送请求请求…...
2023年行研行业研究报告
第一章 行业概述 1.1 行研行业 行业定义为同一类别的经济活动,这涉及生产相似产品、应用相同生产工艺或提供同类服务的集合,如食品饮料行业、服饰行业、机械制造行业、金融服务行业和移动互联网行业等。 为满足全球金融业的需求,1999年8月…...

linux上vscode中.cpp文件中引入头文件.hpp时报错:找不到头文件(启用错误钵形曲线)
当在.cpp文件中引入系统给定的头文件时:#include < iostream > 或者引入自定义的头文件 :#include <success.hpp> 报错:找不到相应的头文件,即在引入头文件的改行底下标出红波浪线 解决方法为: &#…...

Sphinx Docstring
入门 — Sphinx documentation pip install sphinx pip install sphinx-rtd-themesphinx-quickstartexport PYTHONPATH"-"make html cd build/htmlpython -m http.server 9121nohup python -m http.server 9121 &...
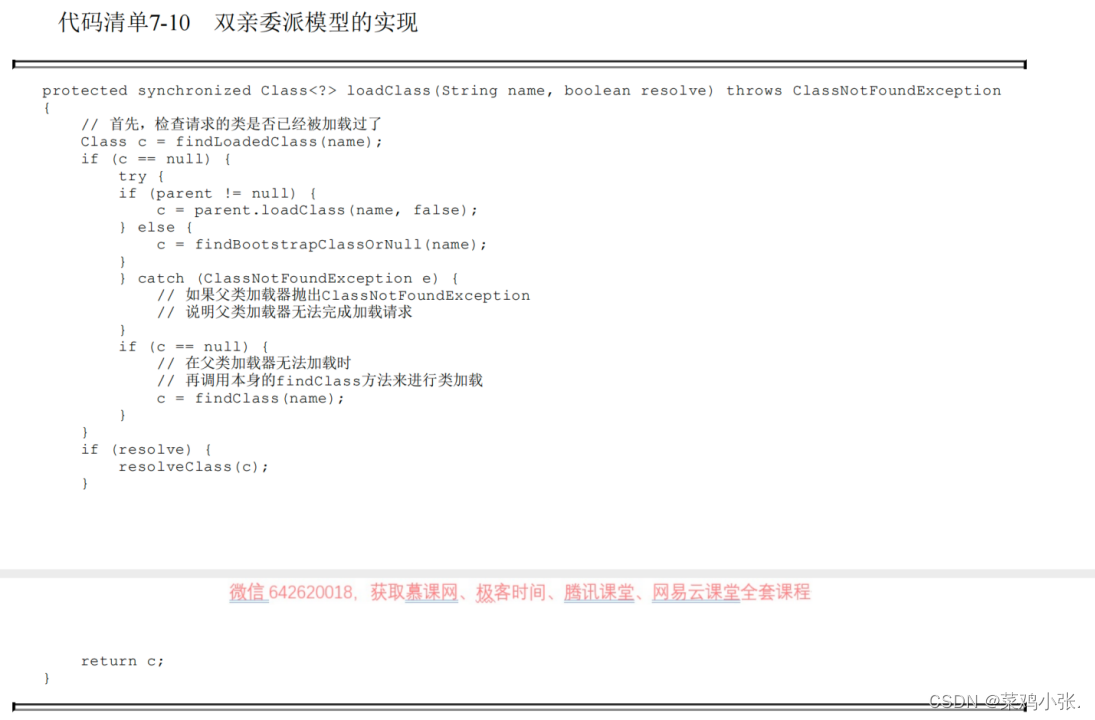
JVM的故事——虚拟机类加载机制
虚拟机类加载机制 文章目录 虚拟机类加载机制一、概述二、类加载的时机三、类加载的过程四、类加载器 一、概述 本章将要讲解class文件如何进入虚拟机以及虚拟机如何处理这些class文件。Java虚拟机把class文件加载到内存,并对数据进行校验、转换解析和初始化&#…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...
