c++搜索基础进阶
搜索算法基础
搜索算法是利用计算机的高性能来有目的的穷举一个问题的部分或所有的可能情况,从而求出问题的解的一种方法。搜索过程实际上是根据初始条件和扩展规则构造一棵解答树并寻找符合目标状态的节点的过程。
所有的搜索算法从其最终的算法实现上来看,都可以划分成两个部分──控制结构和产生系统,而所有的算法的优化和改进主要都是通过修改其控制结构来完成的。现在主要对其控制结构进行讨论,因此对其产生系统作如下约定:
Function ExpendNode(Situation:Tsituation;ExpendWayNo:Integer):TSituation;
表示对给出的节点状态Sitution采用第ExpendWayNo种扩展规则进行扩展,并且返回扩展后的状态。(本文所采用的算法描述语言为类Pascal。)
第一部分 基本搜索算法
一、回溯算法
回溯算法是所有搜索算法中最为基本的一种算法,其采用了一种“走不通就掉头”思想作为其控制结构,其相当于采用了先根遍历的方法来构造解答树,可用于找解或所有解以及最优解。具体的算法描述如下:
[非递归算法]
<Type>
Node(节点类型)=Record Situtation:TSituation(当前节点状态);
Way-NO:Integer(已使用过的扩展规则的数目);
End
<Var>
List(回溯表):Array[1..Max(最大深度)] of Node;
pos(当前扩展节点编号):Integer;
<Init>
List<-0;
pos<-1;
List[1].Situation<-初始状态;
<Main Program>
While (pos>0(有路可走)) and ([未达到目标]) do
Begin
If pos>=Max then (数据溢出,跳出主程序);
List[pos].Way-NO:=List[pos].Way-No+1;
If (List[pos].Way-NO<=TotalExpendMethod= then (如果还有没用过的扩展规则)
Begin
If (可以使用当前扩展规则) then
Begin
(用第way条规则扩展当前节点)
List[pos+1].Situation:=ExpendNode(List[pos].Situation,List[pos].Way-NO);
List[pos+1].Way-NO:=0;
pos:=pos+1;
End-If;
End-If
Else Begin
pos:=pos-1;
End-Else
End-While;
[递归算法]
Procedure BackTrack(Situation:TSituation;deepth:Integer);
Var I :Integer;
Begin
If deepth>Max then (空间达到极限,跳出本过程);
If Situation=Target then (找到目标);
For I:=1 to TotalExpendMethod do
Begin
BackTrack(ExpendNode(Situation,I),deepth+1);
End-For;
End;
范例:一个M*M的棋盘上某一点上有一个马,要求寻找一条从这一点出发不重复的跳完棋盘上所有的点的路线。
评价:回溯算法对空间的消耗较少,当其与分枝定界法一起使用时,对于所求解在解答树中层次较深的问题有较好的效果。但应避免在后继节点可能与前继节点相同的问题中使用,以免产生循环。
二、深度搜索与广度搜索
深度搜索与广度搜索的控制结构和产生系统很相似,唯一的区别在于对扩展节点选取上。由于其保留了所有的前继节点,所以在产生后继节点时可以去掉一部分重复的节点,从而提高了搜索效率。这两种算法每次都扩展一个节点的所有子节点,而不同的是,深度搜索下一次扩展的是本次扩展出来的子节点中的一个,而广度搜索扩展的则是本次扩展的节点的兄弟节点。在具体实现上为了提高效率,所以采用了不同的数据结构.
[广度搜索]
<Type>
Node(节点类型)=Record
Situtation:TSituation(当前节点状态);
Level:Integer(当前节点深度);
Last :Integer(父节点);
End
<Var>
List(节点表):Array[1..Max(最多节点数)] of Node(节点类型);
open(总节点数):Integer;
close(待扩展节点编号):Integer;
New-S:TSituation;(新节点)
<Init>
List<-0;
open<-1;
close<-0;
List[1].Situation<- 初始状态;
List[1].Level:=1;
List[1].Last:=0;
<Main Program>
While (close<open(还有未扩展节点)= and
(open<Max(空间未用完)= and
(未找到目标节点) do
Begin
close:=close+1;
For I:=1 to TotalExpendMethod do(扩展一层子节点)
Begin
New-S:=ExpendNode(List[close].Situation,I);
If Not (New-S in List) then
(扩展出的节点从未出现过)
Begin
open:=open+1;
List[open].Situation:=New-S;
List[open].Level:=List[close].Level+1;
List[open].Last:=close;
End-If
End-For;
End-While;
[深度搜索]
<Var>
Open:Array[1..Max] of Node;(待扩展节点表)
Close:Array[1..Max] of Node;(已扩展节点表)
openL,closeL:Integer;(表的长度)
New-S:Tsituation;(新状态)
<Init>
Open<-0; Close<-0;
OpenL<-1;CloseL<-0;
Open[1].Situation<- 初始状态;
Open[1].Level<-1;
Open[1].Last<-0;
<Main Program>
While (openL>0) and (closeL<Max= and (openL<Max= do
Begin
closeL:=closeL+1;
Close[closeL]:=Open[openL];
openL:=openL-1;
For I:=1 to TotalExpendMethod do(扩展一层子节点)
Begin
New-S:=ExpendNode(Close[closeL].Situation,I);
If Not (New-S in List) then
(扩展出的节点从未出现过)
Begin
openL:=openL+1;
Open[openL].Situation:=New-S;
Open[openL].Level:=Close[closeL].Level+1;
Open[openL].Last:=closeL;
End-If
End-For;
End;
范例:迷宫问题,求解最短路径和可通路径。
评价:广度搜索是求解最优解的一种较好的方法,在后面将会对其进行进一步的优化。而深度搜索多用于只要求解,并且解答树中的重复节点较多并且重复较难判断时使用,但往往可以用A*或回溯算法代替。
第二部分 搜索算法的优化
一、双向广度搜索
广度搜索虽然可以得到最优解,但是其空间消耗增长太快。但如果从正反两个方向进行广度搜索,理想情况下可以减少二分之一的搜索量,从而提高搜索速度。
范例:有N个黑白棋子排成一派,中间任意两个位置有两个连续的空格。每次空格可以与序列中的某两个棋子交换位置,且两子的次序不变。要求出入长度为length的一个初始状态和一个目标状态,求出最少的转化步数。
问题分析:该题要求求出最少的转化步数,但如果直接使用广度搜索,很容易产生数据溢出。但如果从初始状态和目标状态两个方向同时进行扩展,如果两棵解答树在某个节点第一次发生重合,则该节点所连接的两条路径所拼成的路径就是最优解。
对广度搜索算法的改进:
1、添加一张节点表,作为反向扩展表。
2、在while循环体中在正向扩展代码后加入反向扩展代码,其扩展过程不能与正向过程共享一个for循环。
3、在正向扩展出一个节点后,需在反向表中查找是否有重合节点。反向扩展时与之相同。
对双向广度搜索算法的改进:
略微修改一下控制结构,每次while循环时只扩展正反两个方向中节点数目较少的一个,可以使两边的发展速度保持一定的平衡,从而减少总扩展节点的个数,加快搜索速度。
二、分支定界
分支定界实际上是A*算法的一种雏形,其对于每个扩展出来的节点给出一个预期值,如果这个预期值不如当前已经搜索出来的结果好的话,则将这个节点(包括其子节点)从解答树中删去,从而达到加快搜索速度的目的。
范例:在一个商店中购物,设第I种商品的价格为Ci。但商店提供一种折扣,即给出一组商品的组合,如果一次性购买了这一组商品,则可以享受较优惠的价格。现在给出一张购买清单和商店所提供的折扣清单,要求利用这些折扣,使所付款最少。
问题分析:显然,折扣使用的顺序与最终结果无关,所以可以先将所有的折扣按折扣率从大到小排序,然后采用回溯法的控制结构,对每个折扣从其最大可能使用次数向零递减搜索,设A为以打完折扣后优惠的价格,C为当前未打折扣的商品零售价之和,则其预期值为A+a*C,其中a为下一个折扣的折扣率。如当前已是最后一个折扣,则a=1。
对回溯算法的改进:
1、添加一个全局变量BestAnswer,记录当前最优解。
2、在每次生成一个节点时,计算其预期值,并与BestAnswer比较。如果不好,则调用回溯过程。
三、A*算法
A*算法中更一般的引入了一个估价函数f,其定义为f=g+h。其中g为到达当前节点的耗费,而h表示对从当前节点到达目标节点的耗费的估计。其必须满足两个条件:
1、h必须小于等于实际的从当前节点到达目标节点的最小耗费h*。
2、f必须保持单调递增。
A*算法的控制结构与广度搜索的十分类似,只是每次扩展的都是当前待扩展节点中f值最小的一个,如果扩展出来的节点与已扩展的节点重复,则删去这个节点。如果与待扩展节点重复,如果这个节点的估价函数值较小,则用其代替原待扩展节点,具体算法描述如下:
范例:一个3*3的棋盘中有1-8八个数字和一个空格,现给出一个初始态和一个目标态,要求利用这个空格,用最少的步数,使其到达目标态。
问题分析:预期值定义为h=|x-dx|+|y-dy|。
估价函数定义为f=g+h。
<Type>
Node(节点类型)=Record
Situtation:TSituation(当前节点状态);
g:Integer;(到达当前状态的耗费)
h:Integer;(预计的耗费)
f:Real;(估价函数值)
Last:Integer;(父节点)
End
<Var>
List(节点表):Array[1..Max(最多节点数)] of Node(节点类型);
open(总节点数):Integer;
close(待扩展节点编号):Integer;
New-S:Tsituation;(新节点)
<Init>
List<-0;
open<-1;
close<-0;
List[1].Situation<- 初始状态;
<Main Program>
While (close<open(还有未扩展节点)) and
(open<Max(空间未用完)) and
(未找到目标节点) do
Begin
Begin
close:=close+1;
For I:=close+1 to open do (寻找估价函数值最小的节点)
Begin
if List[i].f<List[close].f then
Begin
交换List[i]和List[close];
End-If;
End-For;
End;
For I:=1 to TotalExpendMethod do(扩展一层子节点)
Begin
New-S:=ExpendNode(List[close].Situation,I)
If Not (New-S in List[1..close]) then
(扩展出的节点未与已扩展的节点重复)
Begin
If Not (New-S in List[close+1..open]) then
(扩展出的节点未与待扩展的节点重复)
Begin
open:=open+1;
List[open].Situation:=New-S;
List[open].Last:=close;
List[open].g:=List[close].g+cost;
List[open].h:=GetH(List[open].Situation);
List[open].f:=List[open].h+List[open].g;
End-If
Else Begin
If List[close].g+cost+GetH(New-S)<List[same].f then
(扩展出来的节点的估价函数值小于与其相同的节点)
Begin
List[same].Situation:= New-S;
List[same].Last:=close;
List[same].g:=List[close].g+cost;
List[same].h:=GetH(List[open].Situation);
List[same].f:=List[open].h+List[open].g;
End-If;
End-Else;
End-If
End-For;
End-While;
对A*算法的改进--分阶段A*:
当A*算法出现数据溢出时,从待扩展节点中取出若干个估价函数值较小的节点,然后放弃其余的待扩展节点,从而可以使搜索进一步的进行下去。
第三部分 搜索与动态规划的结合
例1. 有一个棋子,其1、6面2、4面3、5面相对。现给出一个M*N的棋盘,棋子起初处于(1,1)点,摆放状态给定,现在要求用最少的步数从(1,1)点翻滚到(M,N)点,并且1面向上。
分析:这道题目用简单的搜索很容易发生超时,特别当M、N较大时。所以可以考虑使用动态规划来解题。对于一个棋子,其总共只有24种状态。在(1,1)点时,其向右翻滚至(2,1)点,向上翻滚至(1,2)点。而任意(I,J)点的状态是由(I-1,J)和(I,J-1)点状态推导出来的。所以如果规定棋子只能向上和向右翻滚,则可以用动态规划的方法将到达(M,N)点的所有可能的状态推导出来。显然,从(1,1)到达(N,M)这些状态的路径时最优的。如果这些状态中有1面向上的,则已求出解。如果没有,则可以从(M,N)点开始广度搜索,以(M,N)点的状态组作为初始状态,每扩展一步时,检查当前所得的状态组是否有状态与到达格子的状态组中的状态相同,如果有,则由动态规划的最优性和广度搜索的最优性可以保证已求出最优解。
例2.给出一个正整数n,有基本元素a,要求通过最少次数的乘法,求出a^n。
分析:思路一:这道题从题面上来看非常象一道动态规划题,a^n=a^x1*a^x2。在保证a^x1和a^x2的最优性之后,a^n的最优性应该得到保证。但是仔细分析后可以发现,a^x1与a^x2的乘法过程中可能有一部分的重复,所以在计算a^n时要减去其重复部分。由于重复部分的计算较繁琐,所以可以将其化为一组展开计算。描述如下:
I:=n;(拆分a^n)
split[n]:=x1;(分解方案)
Used[n]:=True;(在乘法过程中出现的数字)
Repeat(不断分解数字)
Used[I-split[I]]:=True;
Used[split[I]]:=True;
Dec(I);
While (I>1) and (not Used[I]) do dec(I);
Until I=1;
For I:=n downto 1 do(计算总的乘法次数)
If Used[I] then count:=count+1;
Result:=count;(返回乘法次数)
思路二:通过对思路一的输出结果的分析可以发现一个规律:
a^19=a^1*a^18
a^18=a^2*a^16
a^16=a^8*a^8
a^8=a^4*a^4
a^4=a^2*a^2
a^2=a*a
对于一个n,先构造一个最接近的2^k,然后利用在构造过程中产生的2^I,对n-2^k进行二进制分解,可以得出解。对次数的计算的描述如下:
count:=0;
Repeat
If n mod 2 = 0 then count:=count+1
Else count:=count+2;
n:=n div 2;
Until n=1;
Result:=count;
反思:观察下列数据:
a^15 a^23 a^27
Cost:5 Cost:6 Cost:6
a^2=a^1*a^1 a^2=a^1*a^1 a^2=a^1*a^1
a^3=a^1*a^2 a^3=a^1*a^2 a^3=a^1*a^2
a^6=a^3*a^3 a^5=a^2*a^3 a^6=a^3*a^3
a^12=a^6*a^6 a^10=a^5*a^5 a^12=a^6*a^6
a^15=a^3*a^12 a^20=a^10*a^10 a^24=a^12*a^12
a^23=a^3*a^20 a^27=a^3*a^24
这些数据都没有采用思路二种的分解方法,而都优于思路二中所给出的解。但是经过实测,思路一二的所有的解的情况相同,而却得不出以上数据中的解。经过对a^2-a^15的数据的完全分析,发现对于一个a^n,存在多个分解方法都可以得出最优解,而在思路一中只保留了一组分解方式。例如对于a^6只保留了a^2*a^4,从而使a^3*a^3这条路中断,以至采用思路一的算法时无法得出正确的耗费值,从而丢失了最优解。所以在计算a^n=a^x1*a^x2的重复时,要引入一个搜索过程。例如:a^15=a^3*a^12,a^12=a^6*a^6,而a^6=a^3*a^3。如果采用了a^6=a^2*a^4,则必须多用一步。
<Type>
Link=^Node; (使用链表结构纪录所有的可能解)
Node=Record
split:Integer;
next :Link;
End;
<Var>
Solution:Array[1..1000] of Link; (对于a^n的所有可能解)
Cost :Array[1..1000] of Integer; (解的代价)
max :Integer; (推算的上界)
<Main Program>
Procedure GetSolution;
Var i,j :Integer;
min,c:Integer;
count:Integer;
temp,tail:Link;
plan :Array[1..500] of Integer;
nUsed:Array[1..1000] of Boolean;
Procedure GetCost(From,Cost:Integer); (搜索计算最优解)
Var temp:Link;
a,b :Boolean;
i :Integer;
Begin
If Cost>c then Exit; (剪枝)
If From=1 then (递归终结条件)
Begin
If Cost<c then c:=Cost;
Exit;
End;
temp:=Solution[From];
While temp<>NIL do (搜索主体)
Begin
a:=nUsed[temp^.Split];
If not a then inc(cost);
nUsed[temp^.Split]:=True;
b:=nUsed[From - temp^.Split];
If not b then inc(cost);
nUsed[From-temp^.Split]:=True;
i:=From-1;
While (i>1) and (not nUsed[i]) do dec(i);
GetCost(i,Cost);
If not a then dec(cost);
If not b then dec(cost);
nUsed[From-temp^.Split]:=b;
nUsed[temp^.Split]:=a;
temp:=temp^.next;
End;
End;
Begin
For i:=2 to Max do(动态规划计算所有解)
Begin
count:=0;
min:=32767;
For j:=1 to i div 2 do (将I分解为I-J和J)
Begin
c:=32767;
FillChar(nUsed,Sizeof(nUsed),0);
nUsed[j]:=True;nUsed[i-j]:=True;
If j=i-j then GetCost(i-j,1)
Else GetCost(i-j,2);
If c<min then
Begin
count:=1;
min:=c;
plan[count]:=j;
End
Else if c=min then
Begin
inc(count);
plan[count]:=j;
End;
End;
new(solution[i]); (构造解答链表)
solution[i]^.split:=plan[1];
solution[i]^.next:=NIL;
Cost[i]:=min;
tail:=solution[i];
For j:=2 to count do
Begin
new(temp);
temp^.split:=plan[j];
temp^.next:=NIL;
tail^.next:=temp;
tail:=temp;
End;
End;
End;
相关文章:

c++搜索基础进阶
搜索算法基础 搜索算法是利用计算机的高性能来有目的的穷举一个问题的部分或所有的可能情况,从而求出问题的解的一种方法。搜索过程实际上是根据初始条件和扩展规则构造一棵解答树并寻找符合目标状态的节点的过程。 所有的搜索算法从其最终的算法实现上来看&#…...

管网水位监测的必要性
城市燃气、桥梁、供水、排水、热力、电力、电梯、通信、轨道交通、综合管廊、输油管线等,担负着城市的信息传递、能源输送、排涝减灾等重要任务,是维系城市正常运行、满足群众生产生活需要的重要基础设施,是城市的生命线。基础设施生命线就像…...

无涯教程-Android - 系统架构
Android操作系统是一堆软件组件,大致分为五个部分和四个主要层,如体系结构图中所示。 Linux内核 底层是Linux-Linux 3.6,带有大约115个补丁,这在设备硬件之间提供了一定程度的抽象,并且包含所有必需的硬件驱动程序&am…...

await接受成功的promise,失败的promise用try catch
在 JavaScript 中,await 关键字用于等待一个 Promise 对象的解决(fulfillment)。下面是一个示例: async function example() {try {const result await doSomethingAsync();console.log(result); // 如果 Promise 成功解决&…...
赞奇科技参与华为云828 B2B企业节,云工作站入选精选产品解决方案
8月27日,由华为云携手上万家伙伴共同发起的第二届 828 B2B 企业节拉开帷幕,围绕五大系列活动,为万千中小企业带来精细化商机对接。 聚焦行业数字化所需最优产品,举办超1000场供需对接会,遍及20多个省100多个城市&…...
Docker私有镜像仓库(Harbor)安装
Docker私有镜像仓库(Harbor)安装 1、什么是Harbor Harbor是类似与DockerHub 一样的镜像仓库。Harbor是由VMware公司开源的企业级的Docker Registry管理项目,它包括权限管理(RBAC)、LDAP、日志审核、管理界面、自我注册、镜像复制和中文支持等功能。Docker容器应用的…...
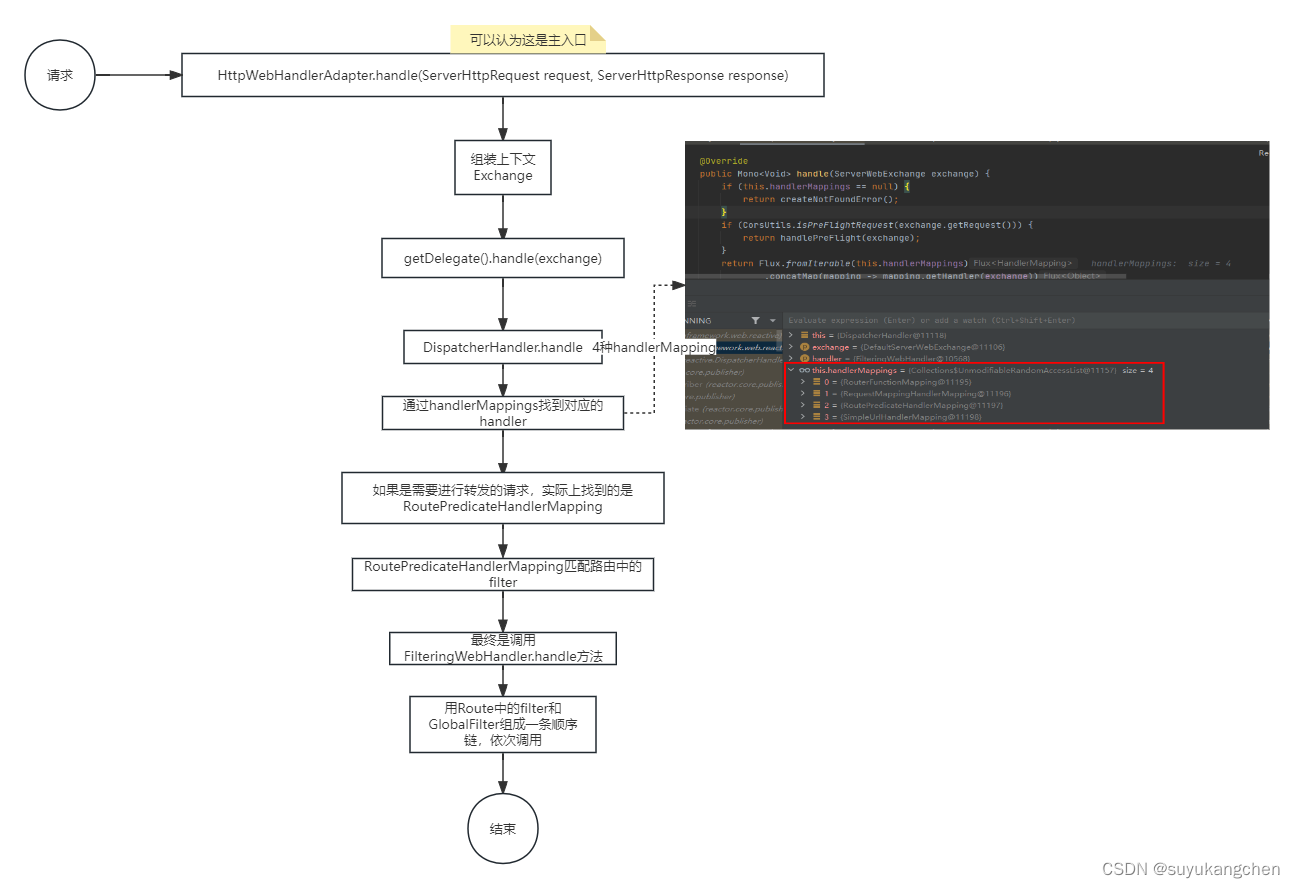
【深入解析spring cloud gateway】06 gateway源码简要分析
上一节做了一个很简单的示例,微服务通过注册到eureka上,然后网关通过服务发现访问到对应的微服务。本节将简单地对整个gateway请求转发过程做一个简单的分析。 一、核心流程 主要流程: Gateway Client向 Spring Cloud Gateway 发送请求请求…...
2023年行研行业研究报告
第一章 行业概述 1.1 行研行业 行业定义为同一类别的经济活动,这涉及生产相似产品、应用相同生产工艺或提供同类服务的集合,如食品饮料行业、服饰行业、机械制造行业、金融服务行业和移动互联网行业等。 为满足全球金融业的需求,1999年8月…...

linux上vscode中.cpp文件中引入头文件.hpp时报错:找不到头文件(启用错误钵形曲线)
当在.cpp文件中引入系统给定的头文件时:#include < iostream > 或者引入自定义的头文件 :#include <success.hpp> 报错:找不到相应的头文件,即在引入头文件的改行底下标出红波浪线 解决方法为: &#…...

Sphinx Docstring
入门 — Sphinx documentation pip install sphinx pip install sphinx-rtd-themesphinx-quickstartexport PYTHONPATH"-"make html cd build/htmlpython -m http.server 9121nohup python -m http.server 9121 &...
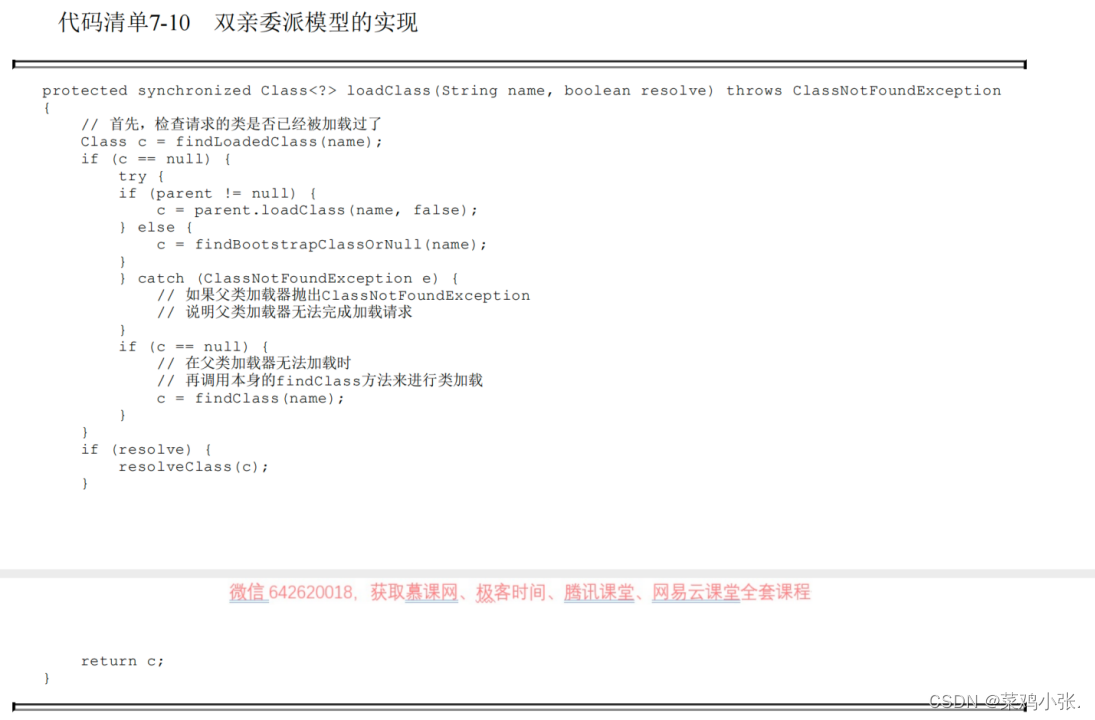
JVM的故事——虚拟机类加载机制
虚拟机类加载机制 文章目录 虚拟机类加载机制一、概述二、类加载的时机三、类加载的过程四、类加载器 一、概述 本章将要讲解class文件如何进入虚拟机以及虚拟机如何处理这些class文件。Java虚拟机把class文件加载到内存,并对数据进行校验、转换解析和初始化&#…...

Sentry 是一个开源的错误监控和日志聚合平台-- 通过docker-compose 安装Sentry
概述 Sentry 是一个开源的错误监控和日志聚合平台,用于帮助开发团队实时监控和调试应用程序中的错误和异常。它可以捕获应用程序中的错误和异常,并提供详细的错误报告,包括错误堆栈跟踪、环境信息、用户信息等。这些报告可以帮助开发团队快速…...
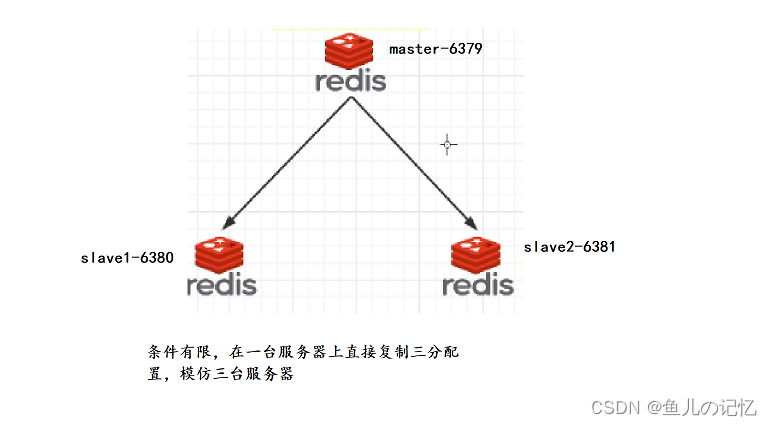
Redis 7 第六讲 主从模式(replica)架构篇
🌹🌹🌹 此篇开始进入架构篇范围(❤艸`❤) 理论 即主从复制,master以写为主,Slave以读为主。当master数据变化的时候,自动将新的数据异步同步到其它slave数据库。 使用场景 读写分离 容灾备份数据备份水平扩容主从架构 演示案例 注:masterauth、replicaof主…...

学习资源记录 =0=
学习路线: 无人机学习路线 无人机学习路线2 自主无人机: 浙大fastlab无人机 机器人理论: 华中科技大学机器人学 C课程 机器人仿真: 2023gazebo仿真开发四足机器人...

Python import包路径管理
import sys sys.path.insert(0, "../")详细链接...

OB Cloud助力泡泡玛特打造新一代分布式抽盒机系统
作为中国潮玩行业的领先者,泡泡玛特凭借 MOLLY、DIMOO、SKULLPANDA 等爆款 IP,以及线上线下全渠道营销收获了千万年轻人的喜爱,会员数达到 2600 多万。2022 年,泡泡玛特实现 46.2 亿元营收,其中线上渠道营收占比 41.8%…...
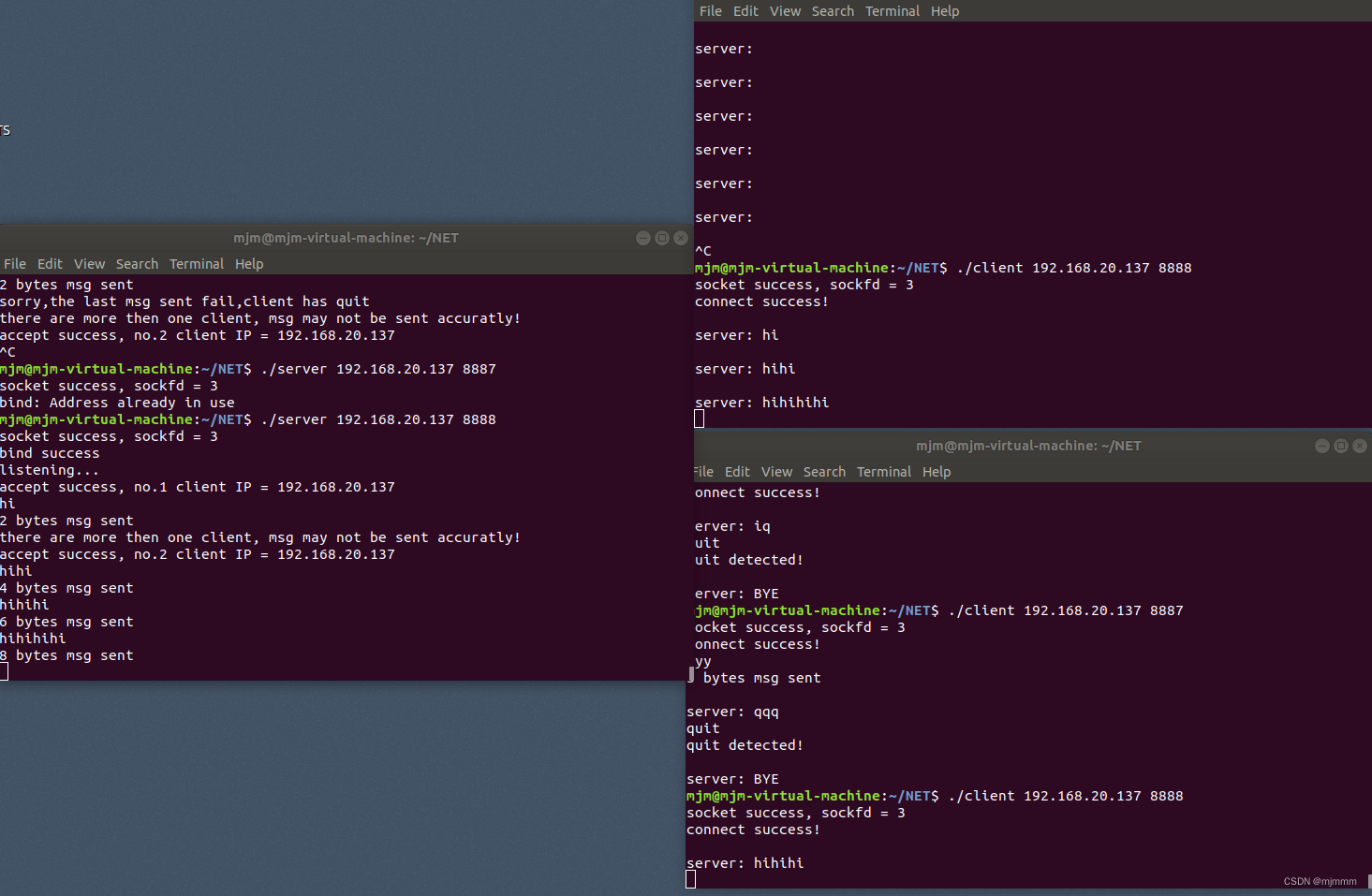
Linux socket网络编程实战(tcp)实现双方聊天
在上节已经系统介绍了大致的流程和相关的API,这节就开始写代码! 回顾上节的流程: 创建一个NET文件夹 来存放网络编程相关的代码: tcp服务端代码初步实现--上 这部分先实现服务器的连接部分的代码并进行验证 server1.cÿ…...

BuhoCleaner for mac:让你的Mac重获新生
你是否曾经因为电脑运行缓慢而感到困扰?是否曾经因为大量的垃圾文件和无效的临时文件而感到头疼?如果你有这样的烦恼,那么BuhoCleaner for mac就是你的救星! BuhoCleaner for mac是一款专门为Mac用户设计的系统清理工具ÿ…...

陶氏公司将出席2023第二届中国汽车碳中和峰会
2023第二届中国汽车碳中和峰会将于10月19日-20日在上海举办。 本次峰会将为行业领导者、政策制定者和专家提供一个平台,讨论汽车行业减少碳排放的策略。专家们将从政策、供应链、ESG、替代能源解决方案、汽车材料创新、法律等不同领域分享碳中和与可持续策略。 通…...

【linux命令讲解大全】051.Linux Awk脚本语言中的字段定界符和流程控制
文章目录 设置字段定界符流程控制语句条件判断语句循环语句while语句for循环do循环 其他语句 数组应用数组的定义读取数组的值数组相关函数二维、多维数组使用 从零学 python 设置字段定界符 默认的字段定界符是空格,可以使用-F “定界符” 明确指定一个定界符&…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...
