【Git】git tag 查看版本号 | 删除本地 | 删除远程仓库| 批量删除
一、删除指定tag
使用场景:比如我们在本地git tag了一个错误的版本号,但是还没有push,想直接删掉避免污染远程仓库
1、删除指令
要删除指定的Git标签(版本号),您可以使用以下命令:
git tag -d 标签名称
2、本地删除
将 标签名称 替换为要删除的标签的名称。例如,要删除名为 “v1.0” 的标签,可以运行以下命令:
# 这将删除本地存储库中的指定标签。
git tag -d v1.0
3、远程仓库删除
如果要删除远程仓库中的标签,您还需要使用以下命令:
git push origin --delete 标签名称
这将删除远程仓库中与指定标签名称匹配的标签。同样,请确保在执行此操作之前,您有适当的权限,并且您了解它可能对共享仓库的其他人产生的影响。
二、批量删除tag
使用场景:比如我们fork了别人的项目,想用做自己的项目去二开一下。但是带过来了很多tag,我们可以直接通过此指令进行删除
1、本地删除
要删除本地Git存储库中的所有标签(tags),您可以使用以下命令:
git tag -l | xargs git tag -d
这个命令的含义是列出所有标签,然后对每个标签执行git tag -d来删除它们。
请注意,这将删除本地存储库中的所有标签,但不会影响远程存储库。
2、远程仓库删除
如果您希望删除远程存储库中的标签,还需要使用git push命令来将这些更改推送到远程仓库,具体取决于您的需求。例如:
git push origin --delete $(git tag -l)
这个命令会删除所有与本地存储库中标签匹配的远程标签。请谨慎操作,确保您的操作不会影响其他协作者或远程仓库。
三、查看tag版本号
使用场景:当我们的tag创建过多的时候,难免会忘记最后一个tag。如果我们使用指令:git tag 去一直翻,会造成时间的浪费
1、查看最后版本号(详细)
要查看当前Git存储库中最后一个标签(tag)的版本号,可以使用以下命令:
git describe --tags --abbrev=0
这个命令会显示最新标签的名称,即版本号。
2、查看最后版本号(简单)
如果您只想要版本号而不包括任何前缀或其他信息,可以使用以下命令:
git describe --tags --abbrev=0 --always
这将返回最新标签的版本号,例如 “v1.0”。如果没有标签,它将返回较短的提交哈希值。
请注意,这些命令只适用于已经存在的标签。如果您的存储库没有标签,它们将不会返回任何内容。
相关文章:

【Git】git tag 查看版本号 | 删除本地 | 删除远程仓库| 批量删除
一、删除指定tag 使用场景:比如我们在本地git tag了一个错误的版本号,但是还没有push,想直接删掉避免污染远程仓库 1、删除指令 要删除指定的Git标签(版本号),您可以使用以下命令: git tag -d 标…...
)
thinkphp:数据库查询,嵌套别的表的查询(别的表做子查询)
例子 从 vendors 表中选择记录。在 vendors 表中,筛选出具有满足以下条件的 vendor_code 值: 对应的采购订单(在 po_headers_all 表中)存在未完全接收的采购行(在 po_lines_all 表中)。相应的采购订单状态…...

《Linux 系统命令及Shell脚本实践指南》
Linux 系统命令及Shell脚本实践指南 《Linux 系统命令及Shell脚本实践指南》该书从结构上分为三部分:第一部分1.1Linux的历史发展1.2用户管理1.3任务管理单一时刻执行一次任务使用at周期性任务使用:cron表达式,命令crontab 1.4文件管理1.4.1 Linux shell…...

代码随想录算法训练营第三十八天 | ● 理论基础 ● 509. 斐波那契数 ● 70. 爬楼梯 ● 746. 使用最小花费爬楼梯
题目链接:509. 斐波那契数 代码随想录 视频:手把手带你入门动态规划 | LeetCode:509.斐波那契数_哔哩哔哩_bilibili 看完代码随想录之后的想法: 我们要知道动态规划的五部曲; 1,确定dp数组的含义&#x…...
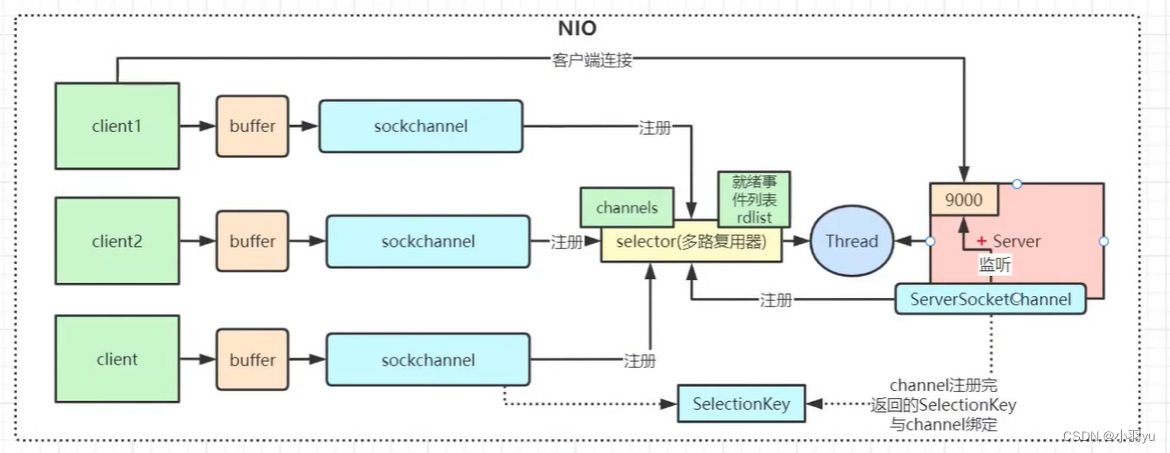
Java分别用BIO、NIO实现简单的客户端服务器通信
分别用BIO、NIO实现客户端服务器通信 BIONIONIO演示(无Selector)NIO演示(Selector) 前言: Java I/O模型发展以及Netty网络模型的设计思想 BIO Java BIO是Java平台上的BIO(Blocking I/O)模型&a…...

React Portals
什么是React Portals React Portals(React 门户)是 React 提供的一种机制,用于将组件渲染到 DOM 树中的不同位置,而不受组件层次结构的限制。它允许你将一个组件的渲染内容“传送”到 DOM 结构中的任何位置,通常用于处…...

Python基础之高级函数
异常捕获 Python中,使用trycatch两个关键字来实现对异常的处理。在我们平时的工作中,异常的出现是在所难免的,但是异常一旦出现,极有可能会直接导致程序崩溃,无法正常运行,所以异常一定要及时的做出对应的…...
CSS3常用的新功能总结
CSS3常用的新功能包括圆角、阴渐变、2D变换、3D旋转、动画、viewpor和媒体查询。 圆角、阴影 border-redius 对一个元素实现圆角效果,是通过border-redius完成的。属性为两种方式: 一个属性值,表示设置所有四个角的半径为相同值ÿ…...
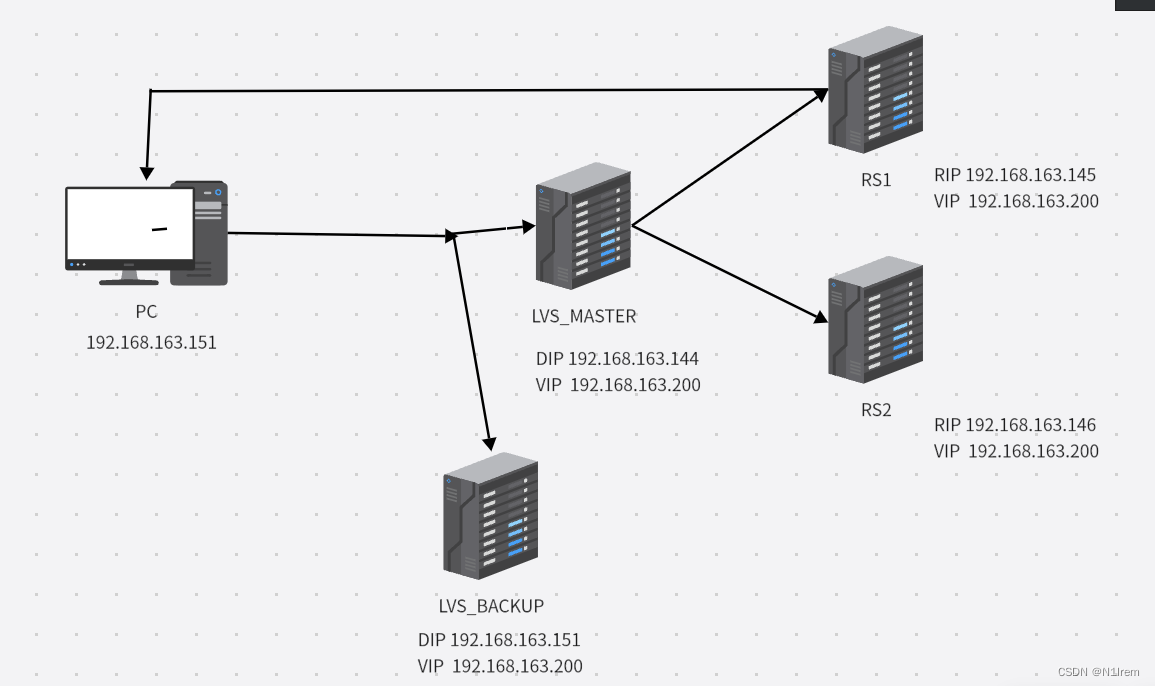
Lvs+KeepAlived高可用高性能负载均衡
目录 1.环境介绍 2.配置keepalived 3.测试 1.测试负载均衡 2.测试RS高可用 3.测试LVS高可用 3.1测试lvs主服务宕机 3.2.测试lvs主服务器恢复 4.我在实验中遇到的错误 1.环境介绍 环境:centos7 RS1---RIP1:192.168.163.145 VIP 192.168.163.200 RS2---RIP2…...

无涯教程-Android Online Test函数
Android在线测试模拟了真正的在线认证考试。您将看到基于 Android概念的多项选择题(MCQ),将为您提供四个options。您将为该问题选择最合适的答案,然后继续进行下一个问题,而不会浪费时间。完成完整的考试后,您将获得在线考试分数。 总问题数-20 最长时间-20分钟 Start Test …...

蓝桥杯打卡Day1
文章目录 全排列八皇后 一、全排列IO链接 本题思路:本题是一道经典的全排列问题,深度优先搜索即可解决。 #include <bits/stdc.h>constexpr int N10;std::string s; std::string ans; int n; bool st[N];void dfs(int u) {if(un){std::cout<<ans<…...

zipkin2.24.2源码install遇见的问题
1、idea导入项目后将Setting中的关于Maven和Java Compile相关的配置改为jdk11,同时Project Structure改为jdk11 2、将pom配置中的fork标签注释 标题未修改以上配置产生的问题 Compilation failure javac: Ч ı : --release : javac <options> <source files&g…...
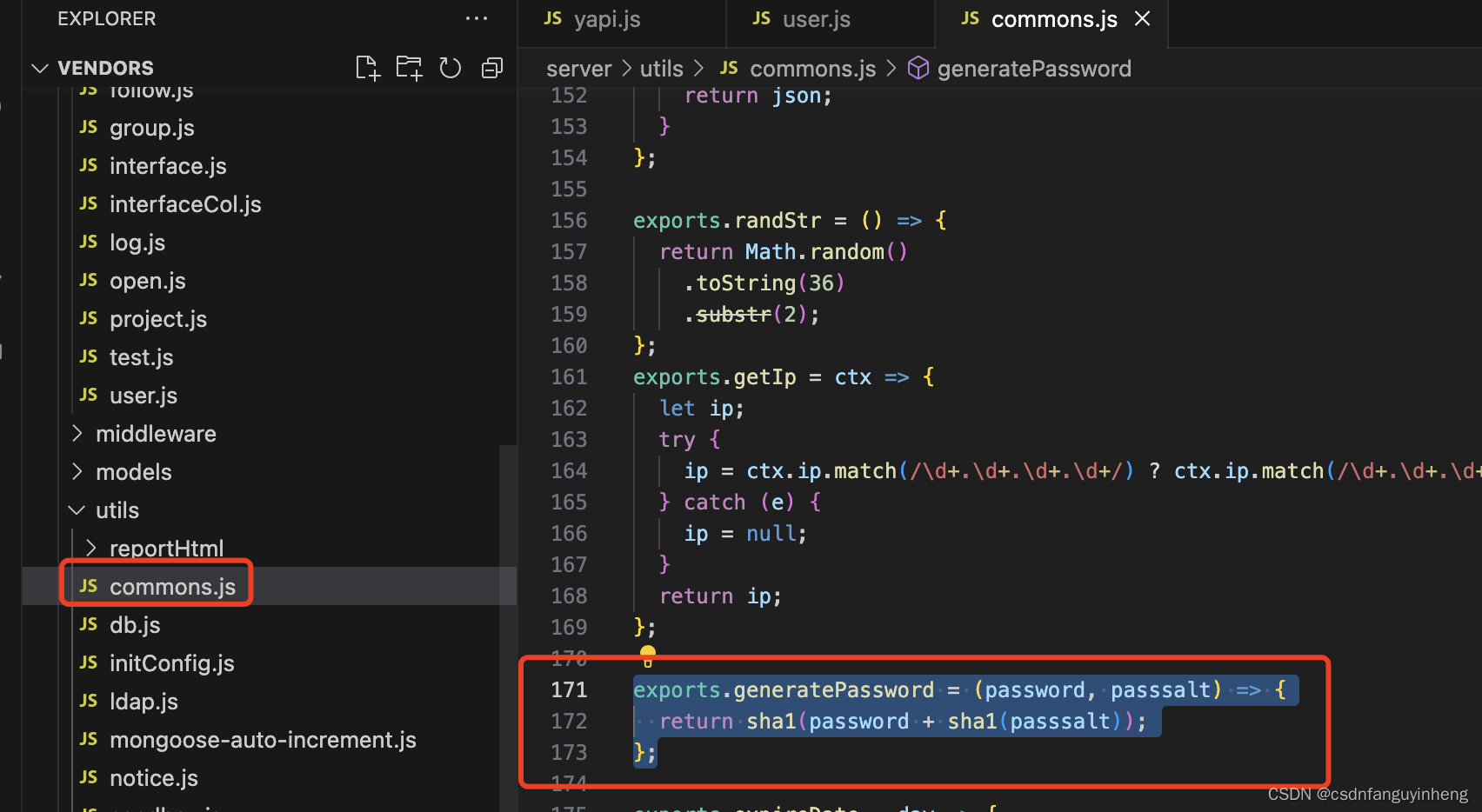
yapi密码是如何生成的
yapi密码是如何生成的 关闭yapi注册功能后,想要通过手动插入用户数据到db中,那么密码是如何生成的呢? exports.generatePassword (password, passsalt) > { return sha1(password sha1(passsalt)); }; 所以如果想要创建一个用户&#x…...

2023-09-02 LeetCode每日一题(最多可以摧毁的敌人城堡数目)
2023-09-02每日一题 一、题目编号 2511. 最多可以摧毁的敌人城堡数目二、题目链接 点击跳转到题目位置 三、题目描述 给你一个长度为 n ,下标从 0 开始的整数数组 forts ,表示一些城堡。forts[i] 可以是 -1 ,0 或者 1 ,其中&…...
k8s环境部署配置
目录 一.虚拟机准备 二.基础环境配置(各个节点都做) 1.IP和hosts解析 2.防火墙和selinux 3.安装基本软件 4.配置时间同步 5.禁用swap分区 6.修改内核参数并重载 7.配置ipvs 三.docker环境(各个节点都做) 1.配置软件源并…...
Java之文件操作与IO
目录 一.认识文件 1.1文件是什么? 1.2文件的组织 1.3文件路径 1.4文件的分类 二.文件操作 2.1File概述 三.文件内容操作--IO 3.1JavaIO的认识 3.2Reader和Writer ⭐Reader类 ⭐Writer类 3.2FileInputStream和FileOutputStream ⭐FileInputStream类 …...

指令系统(408)
一、拓展操作码指令格式 【2017 统考】某计算机按字节编址,指令字长固定且只有两种指令格式,其中三地址指令29条、二地址指令107条,每个地址字段6位,则指令字长至少应该是( A) A、24位 B、26位 …...
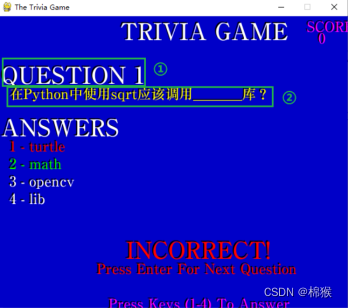
Pygame中Trivia游戏解析6-3
3.3 Trivia类的show_question()函数 Trivia类的show_question()函数的作用是显示题目。主要包括显示题目框架、显示题目内容和显示题目选项等三部分。 3.3.1 显示题目的框架 在show_question()函数中,通过以下代码显示题目的框架。 print_text(font1, 210, 5, &q…...
热释电矢量传感器设计
1 概述 使用4个热释电传感器组成一个2X2的矩阵。通过曲线的相位差、 峰峰值等特征量来计算相关信息。本文使用STM32单片机设计、制作了热释电传感器矩阵;使用C#.NET设计了上位机软件。为以上研究做了试验平台。 2 硬件电路设计 2.1 热释电传感器介绍 热释电红外…...

MySql学习笔记10——视图介绍
视图 概述 view view可以看作是一张“虚拟表”,(但是他也是会作为文件存在的) 当我们通过复杂的查询语句获取一张表的时候,可以将这张表作为一个视图,和创建一个新表不同,在视图上进行的DML操作会对数据…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...
