熵权法计算权重
文章目录
- 1. 多属性决策问题
- 2. 熵(entropy)
- 3. 信息熵
- 4. 熵权法
- 5. 熵权法的实现
基于信息论的熵值法是根据各指标所含信息有序程度的差异性来确定指标权重的客观赋权方法,仅依赖于数据本身的离散程度。
熵用于度量不确定性,指标的离散程度越大(不确定性越大)则熵值越大,表明指标值提供的信息量越多,则该指标的权重也应越大。
1. 多属性决策问题
熵权法多用于多属性决策问题中求解各个属性的权值。我们先简单介绍下多属性决策:
多属性决策指的是在考虑多个属性的情况下,对一组(有限个)备选方案进行排序或者择优。
主要包含以下几个组成部分:
(1)获取属性信息。
(2)属性权重确定:包括主观赋权法、客观赋权法、主客观结合的赋权法。
(3)多属性决策:对决策所需的属性信息进行集结,并基于相应策略对备选方案进行排序和择优。
这里,假设我们的数据的样本数量为nnn,每个样本有jjj个feature,那么对于一个样本的一个feature的取值为: xijx_{ij}xij
其中:
iii :第个样本
jjj :第个feature
假设有这样一个应用场景,由于每一个样本都有很多feature,我想把这个样本的这些feature总结为一个值,应该怎么做?即

我们有一万种方法能达到这个目的,有了这个值,我们就可以进行排名、比较等操作。所以,这个值还得有点实际意义,不能是瞎攒出来的一个数。
熵权法(EEM, entropy evaluation method)是根据指标信息熵的大小对指标客观赋值的一种方法,信息熵越大,代表该指标的离散程度很大,包含的信息就多,所赋予的权重就越大。也就是说,这个方法实际上关注的是变量的取值的多样性,取值大小差异越大的,即离散程度越高的,就说明这个feature的重要程度很大,包含了更多的信息。
2. 熵(entropy)
熵的概念是由德国物理学家克劳修斯于1865年所提出。最初是用来描述“能量退化”的物质状态参数之一,在热力学中有广泛的应用。
热力学第二定律又被称为”熵增“定律,从它的描述中大家也能明白一二:在自然状态下,热量只会从热水杯传递给冷水杯,这个过程是不可逆的,而”熵“则是这个不可逆过程的度量。换而言之,封闭系统的熵只会不变或增加,不会减少。关于“热力学熵”,最原始的宏观表达式是:
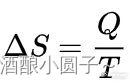
那时的熵仅仅是一个可以通过热量改变来测定的物理量,其本质仍没有很好的解释,直到统计物理、信息论等一系列科学理论发展,熵的本质才逐渐被解释清楚,即,熵的本质是一个系统“内在的混乱程度”。
3. 信息熵
信息熵是一个数学上颇为抽象的概念,由大名鼎鼎的信息论之父——克劳德 • 香农提出。在这里不妨把信息熵理解成某种特定信息的出现概率(离散随机事件的出现概率)。一个系统越是有序,信息熵就越低;反之,一个系统越是混乱,信息熵就越高。信息熵也可以说是系统有序化程度的一个度量。
一般说来,信息熵的表达式为:
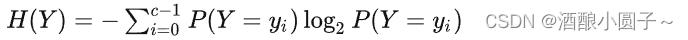
举例1:
假设一个硬币,投出正反两面的概率都是50%,那么它的entropy为:
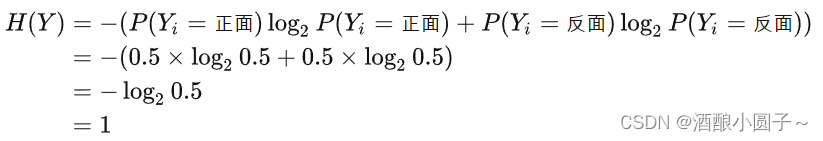
也就是说,一个公平的硬币,其正反面概率都是50%的情况下,熵最大化了。这件事推广到有多个面的骰子也是一样的,每个事件出现的概率越接近,样本的混乱程度就越高,熵就越大。而如果某个事件的出现概率是压倒性的,比其他所有事件出现概率加一起都高得多,那么熵就会比较小。
举例2:
假设4个元素,每个元素的feature有1个特征x1,并且它有个类型y,即


我们发现一个很有趣的现象,就是进行分组以后,熵降低了。这实际上就是决策树的基本原理,通过对属性进行分割,从而降低整体的混乱程度。即对一个属性的不同取值进行分组以后,每一组的混乱程度做个加权和,整体混乱程度要比分组之前的混乱程度还要低,也就是说每一组都更纯粹一些。
当然,这里计算entropy的log2log_2log2是以2为底,也可以以自然对数为底,函数图像形状是基本不变的。
4. 熵权法
回到最开始我们问的问题,就是我怎么对一大堆指标(feature)进行综合一下,形成一个综合的值。当然我们就是用简单的加权和来做,但是我们还希望这个值具有一定的代表性。这个代表性我们就视为该feature下取值的多样性,或者说离散程度。
也就是说,如果一张数据表有很多行数据,每个数据又有很多feature,**如果某个feature的取值大家都一样,这实际上也说明这个feature可以丢掉了,用什么数据训练模型它都没啥用。但如果这个feature的取值特别多,那么这么指标对于决策更有用。**因此我们如果要综合一个指标的话,我们就要给最多样化,即离散程度最高的feature以最高的权重。
主要计算步骤如下:
(1)归一化数据
这里对数据进行归一化,主要是消除量纲的影响。可以采用 min-max归一化或者mean-std归一化方法。
数据归一化方法可以参考博客:数据预处理——数据无量纲化(归一化、标准化)
这里以min-max归一化为例:

这里有几点需要注意的:
- 如果原始数据中,不同属性的取值在相近的量级上,xmaxx_{max}xmax和xminx_{min}xmin可以直接取所有数据的最大最小值。
X_std = (X - np.min(X)) / (np.max(X) - np.min(X)
- 如果原始数据中,不同属性的取值量级相差较大,可以考虑使用列归一化,即xmaxx_{max}xmax和xminx_{min}xmin取列数据的列最大值和列最小值。
X_std = (X - X.min(axis=0)) / (X.max(axis=0) - X.min(axis=0))
- 如果原始数据中,某个属性的取值完全一样为xvx_{v}xv,min、max、x 均相等,则基于min-max归一化方法计算分子分母均为0,默认算出的该属性数据均为0。
该属性的取值大家都一样,对于决策没有作用,参与决策过程的权重理应很小很小。而归一化后的0值数据,经过信息熵的计算后,P=1P=1P=1, log(P)=0log(P)=0log(P)=0,−P∗log(P)=0-P * log(P) = 0−P∗log(P)=0,E=0E = 0E=0,安全权重系数计算公式,最后算出来的权值很大,不符合实际情况。
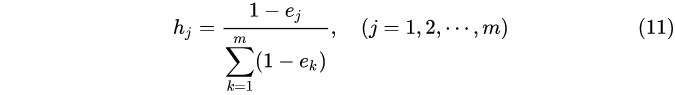
这种情况下,我们可以在数据归一化后,给数据加上一个很小的数值(比如1e-3)来避免样本取值为0情况,即:x′′ij=xij′+0.001{x''}_{ij}=x'_{ij} + 0.001x′′ij=xij′+0.001
(2)只关注第jjj个feature,计算每个样本x′′ij{x''}_{ij}x′′ij在第个feature下所占的全部取值的比例。

这个比例其实就是视为概率了。
举个例子,如果对于第jjj个feature,我们的样本经过归一化以后取值为:

我们可以理解为,取值越大,这个pijp_{ij}pij的值就越大。相当于我们自定义了一个"概率",将其与取值联系到了一起,这么做,是因为我们要计算的熵仅仅与概率有关,而如果xijx_{ij}xij的取值特别多样化,我们用它算出来的这个概率也会特别多样化,有大有小,从而降低熵。
(3)计算第jjj个feature的熵。

(4)计算第jjj个feature的差异系数。

这个差异系数的含义显而易见,就是该feature的离散程度越高,该差异系数越高。
(5)对差异系数归一化,计算第个feature的权重

这样对于每个feature,其离散程度越高,所占比重就会越高。这样一来,我们就有了每个feature的权重了,下面我们用这个权重来算每个样本的指标
(6)计算最终的统计测度:

5. 熵权法的实现
先定义基础数据:
data = pd.DataFrame({'人均专著': [0.1, 0.2, 0.4, 0.9, 1.2], '生师比': [5, 6, 7, 10, 2], '科研经费': [5000, 6000, 7000, 10000, 400],'逾期毕业率': [4.7, 5.6, 6.7, 2.3, 1.8]}, index=['院校' + i for i in list('ABCDE')])【实现代码 1】:
import numpy as npdef get_entropy_weight_1(data): # 熵权法需要使用原始数据作为输入data = np.array(data)# 数据归一化# 这里可以根据需要选择mean-std归一化或者min-max归一化# 计算PijP = data / data.sum(axis=0) # 需要考虑分子为0的情况,可以考虑加一个epsilon=1e-3# 计算熵值E = np.nansum(-P * np.log(P) / np.log(len(data)), axis=0)# 计算权系数return (1 - E) / (1 - E).sum()get_entropy_weight_1(data)
程序输出结果:
array([ 0.41803075, 0.14492264, 0.28588943, 0.15115718])
【实现代码 2】:
def get_entropy_weight_2(data):""":param data: dataframe类型:return: 各指标权重列表"""# 数据归一化# 这里可以根据需要选择mean-std归一化或者min-max归一化m,n=data.shape#将dataframe格式转化为matrix格式data=data.as_matrix(columns=None)# 第一步:计算kk=1/np.log(m)#第二步:计算pijpij=data/data.sum(axis=0)# 第三步:计算每种指标的信息熵tmp=np.nan_to_num(pij*np.log(pij))ej=-k*(tmp.sum(axis=0))# 第四步:计算每种指标的权重wi=(1-ej)/np.sum(1-ej)wi_list=list(wi)return wi_listget_entropy_weight_2(data)
[0.41803075156086411,0.14492263660659988,0.28588943395852595,0.15115717787401006]
可以看到,两个代码的输出结果一致,且各个属性的权值加起来和为1。
这里,有几个需要注意的点:
- 数据归一化:在原始数据量纲不一致时,我们使用熵权法之前可以先对数据做归一化处理。这里可以根据数据的实际情况和业务需要选择mean-std归一化或者min-max归一化。不同的归一化方法,对最后求出来的权值会有影响。
- 可以在数据归一化后,给数据加上一个很小的数值(比如1e-3)来避免样本取值为0情况,即:x′′ij=xij′+0.001{x''}_{ij}=x'_{ij} + 0.001x′′ij=xij′+0.001
- 除数为0的情况:上述计算过程涉及除法,会遇到除数为0的情况。可以给除数加一个很小的数值,如epsilon=1e-3,以避免除以0的情况发生。
【参考博客】:
- TOPSIS法(优劣解距离法)介绍及 python3 实现
- https://zhuanlan.zhihu.com/p/551107230
相关文章:

熵权法计算权重
文章目录1. 多属性决策问题2. 熵(entropy)3. 信息熵4. 熵权法5. 熵权法的实现基于信息论的熵值法是根据各指标所含信息有序程度的差异性来确定指标权重的客观赋权方法,仅依赖于数据本身的离散程度。熵用于度量不确定性,指标的离散…...

redis实现用户签到,统计活跃用户,用户在线状态,用户留存率
开发的过程中,可能会遇到用户签到、统计当天的活跃用户、以及每个用户的在线状态,用户留存率的开发需求,可能会用传统的方法,根据相应的需求设计数据库表等,但这样耗费的存储空间大,以及性能方面也不会太好…...
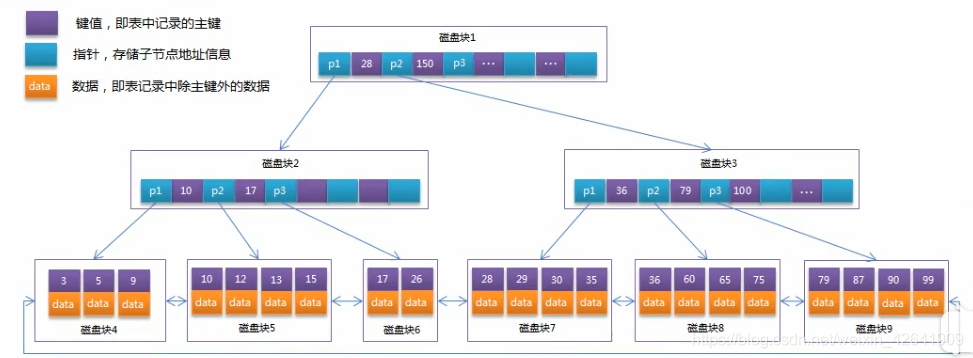
MySQL中有多少种索引?索引的底层实现原理
索引存储在内存中,为服务器存储引擎为了快速找到记录的一种数据结构。索引的主要作用是加快数据查找速度,提高数据库的性能。索引的分类(1) 普通索引:最基本的索引,它没有任何限制。(2) 唯一索引:与普通索引类似&#…...
以及线索二叉树java详解)
LeetCode经典算法题:二叉树遍历(递归遍历+迭代遍历+层序遍历)以及线索二叉树java详解
LeetCode经典算法题:二叉树遍历(递归遍历迭代遍历层序遍历)以及线索二叉树java详解 文章目录二叉树遍历题目描述解题思路与代码递归遍历迭代遍历层序遍历线索二叉树:二叉树遍历 题目描述 从根节点往下查找,先找左子树…...

【Java闭关修炼】MyBatis-接口代理的方式实现Dao层
【Java闭关修炼】MyBatis-接口代理的方式实现Dao层实现规则代码实现代理对象分析接口代理方式小结实现规则 映射配置文件中的名称空间必须和Dao层接口的全类名相同映射配置文件的增删改查标签的id属性必须和Dao层接口方法的参数相同映射配置文件中的增删改查标签的parameterTyp…...

2022年网络安全政策态势分析与2023年立法趋势
近日,公安部第三研究所网络安全法律研究中心与 360 集团法务中心联合共同发布了《全球网络安全政策法律发展年度报告(2022)》。《报告》概览2022年全球网络安全形势与政策法律态势,并对2023年及后续短期内网络安全政策、立法趋势进…...
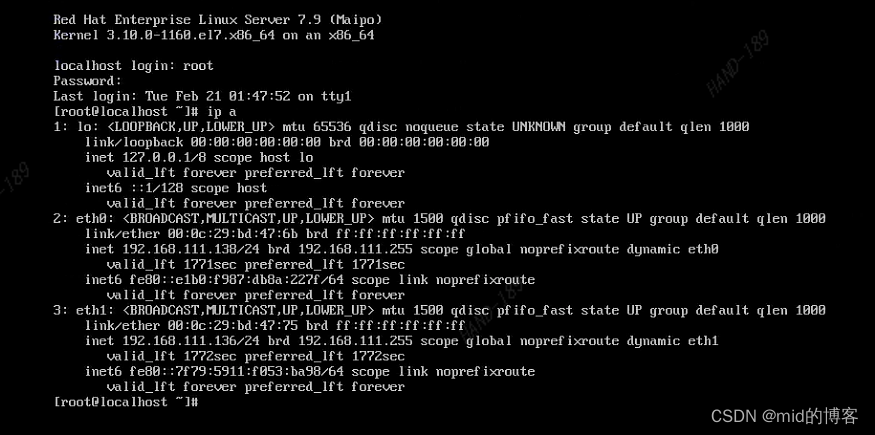
使用vmware制作云平台redhat7.9镜像模板
一、概述 1.1 redhat7.9 定制镜像上传到云平台。 这个制作镜像得方式适用于多种iso 镜像。 将iso 镜像通过vmware 创建出一台虚机,对虚机做一些基础配置。在虚机上安装kvm 虚拟化得工具, 将iso 镜像在导入虚机种通过kvm创建一下虚机, 虚机创…...

OpenCV基础(28)使用OpenCV进行摄像机标定Python和C++
摄像头是机器人、监控、太空探索、社交媒体、工业自动化甚至娱乐业等多个领域不可或缺的一部分。 对于许多应用,必须了解相机的参数才能有效地将其用作视觉传感器。 在这篇文章中,您将了解相机校准所涉及的步骤及其意义。 我们还共享 C 和 Python 代码以…...

APB总线详解及手撕代码
本文的参考资料为官方文档AMBA™3 APB Protocol specification文档下载地址: https://pan.baidu.com/s/1Vsj4RdyCLan6jE-quAsEuw?pwdw5bi 提取码:w5bi APB端口介绍介绍总线具体握手规则之前,需要先熟悉一下APB总线端口,APB的端口…...

【Linux/Windows】源文件乱码问题解决方法总结
🐚作者简介:花神庙码农(专注于Linux、WLAN、TCP/IP、Python等技术方向)🐳博客主页:花神庙码农 ,地址:https://blog.csdn.net/qxhgd🌐系列专栏:Linux技术&…...
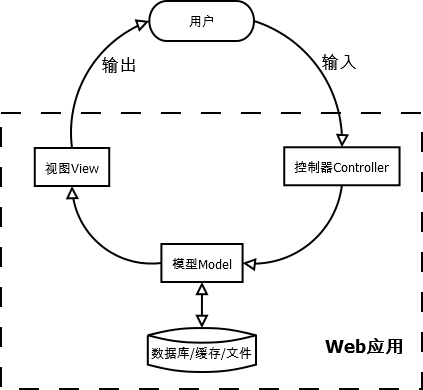
Python 四大主流 Web 编程框架
目前Python的网络编程框架已经多达几十个,逐个学习它们显然不现实。但这些框架在系统架构和运行环境中有很多共通之处,本文带领读者学习基于Python网络框架开发的常用知识,及目前的4种主流Python网络框架:Django、Tornado、Flask、Twisted。 …...
学UI设计,可以向哪些方向发展?该怎么学?
1、什么是UI设计?UI设计,全称 User Interface,翻译成中文意思叫做用户界面设计。2、UI设计的类型UI设计按用户和界面来分可分成四种UI设计。分别是移动端UI设计,PC端UI设计,游戏UI设计,以及其它UI设计。第一…...
【C++】初识CC++内存管理
前言 我们都知道C&C是非常注重性能的语言,因此对于C&C的内存管理是每一个C/C学习者必须重点掌握的内容,本章我们并不是深入讲解C&C内存管理,而是介绍C&C内存管理的基础知识,为我们以后深入理解C&C内存管理做铺…...
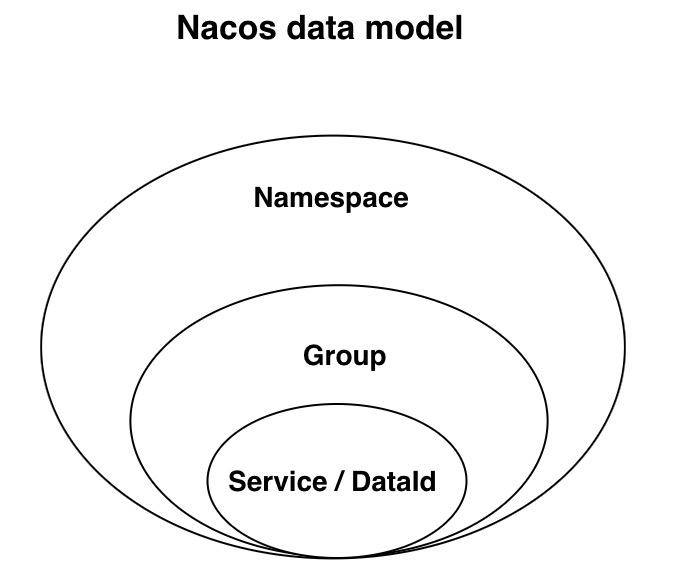
Nacos快速使用指南
简单例子:springboot快速集成nacos官方github文档命名空间是绝对隔离的。group之间可以通过配置实现跨 group访问配置中心Nacos config官方文档应用级别的默认配置文件名(dataId)dataId 的完整格式如下:${prefix}-${spring.profil…...
复旦发布国内首个类ChatGPT模型MOSS,和《流浪地球》有关?
昨晚,复旦大学自然语言处理实验室邱锡鹏教授团队发布国内首个类ChatGPT模型MOSS,现已发布至公开平台https://moss.fastnlp.top/ ,邀公众参与内测。 MOSS和ChatGPT一样,开发的过程也包括自然语言模型的基座训练、理解人类意图的对…...
国家级高新区企业主要经济指标(2012-2021年)
数据来源:国家统计局 时间跨度:2012-2021 区域范围:全国(及各分类统计指标) 指标说明:手工提取最新的中国统计年鉴数据中各个excel指标表,形成各个指标文件的多年度数据,便于多年…...
SpringBoot2核心技术-核心功能【05、Web开发】
目录 1、SpringMVC自动配置概览 2、简单功能分析 2.1、静态资源访问 1、静态资源目录 2、静态资源访问前缀 2.2、欢迎页支持 2.3、自定义 Favicon 2.4、静态资源配置原理 3、请求参数处理 0、请求映射 1、rest使用与原理 2、请求映射原理 1、普通参数与基本注解 …...
等级考试试卷(六级)解析)
2021-03 青少年软件编程(C语言)等级考试试卷(六级)解析
2021-03 青少年软件编程(C语言)等级考试试卷(六级)解析T1. 生日相同 2.0 在一个有180人的大班级中,存在两个人生日相同的概率非常大,现给出每个学生的名字,出生月日。试找出所有生日相同的学生。 时间限制:1000 内存限制:65536 输入 第一行为整数n,表示有n个学生,n …...

数据库的多租户隔离
数据库的多租户隔离有三种方案 1、独立数据库 一个租户一个数据库,这种方案的用户数据隔离级别最高,安全性最好,成本也最高 优点:为不同的租户提供独立的数据库,有助于简化数据模型的扩展设计,满足不同租…...

网络输入分辨率是否越大越好
目标检测比如 yolov5,训练输入图像大小默认是 640*640,这个是不是越大训练的效果越好 ? 这个肯定不是的。而且,如果仅调整输入图像的分辨率,不改变网络结构的话,检测准确率反而会下降的。首先,…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...
