机器学习丨2. 线性回归(Linear Regression)
Author:AXYZdong 硕士在读 工科男
有一点思考,有一点想法,有一点理性!
定个小小目标,努力成为习惯!在最美的年华遇见更好的自己!
CSDN@AXYZdong,CSDN首发,AXYZdong原创
唯一博客更新的地址为: 👉 AXYZdong的博客 👈
B站主页为:AXYZdong的个人主页
AI专栏
- ⭐⭐⭐【AI常用框架和工具】(点击跳转)
包括常用工具Numpy、Pandas、Matplotlib,常用框架Keras、TensorFlow、PyTorch。理论知识结合代码实例,常用工具库结合深度学习框架,适合AI的初学者入门。
文章目录
- AI专栏
- 1 线性回归算法原理
- 1.1 一元线性回归的算法过程
- 1.2 多元线性回归
- 2 线性回归算法优化
- 2.1 求解多元回归的系数
- 2.2 过拟合问题解决方法
- 2.3 线性回归的模型评估方法
- 3 线性回归代码实现
- 3.1 一元线性回归Python底层实现
- 3.2 多元线性回归的实现
- 3.3 线性回归第三方库实现
1 线性回归算法原理
1.1 一元线性回归的算法过程
-
首先确定目标:尽可能地拟合样本数据集,即使误差最小化。带着这个思想去寻找我们的损失函数。
-
由于误差服从高斯分布:
p ( ε i ) = 1 2 π σ exp ( − ε i 2 2 σ 2 ) p\left(\varepsilon_i\right)=\frac{1}{\sqrt{2 \pi }\sigma} \exp \left(-\frac{\varepsilon_i^2}{2 \sigma^2}\right) p(εi)=2πσ1exp(−2σ2εi2) -
将误差函数带入上式:
P ( y i ∣ x i ; w ) = 1 2 π σ exp ( − ( y i − ( ω X i + b ) ) 2 2 σ 2 ) P\left(y_i \mid x_i ; w\right)=\frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{\left(y_i-\left(\omega X_i+b\right)\right)^2}{2 \sigma^2}\right) P(yi∣xi;w)=2πσ1exp(−2σ2(yi−(ωXi+b))2) -
似然函数:
L ( w ) = Π i = 1 m 1 2 π σ exp ( − ( y i − ( ω X i + b ) ) 2 2 σ 2 ) L(w)=\Pi_{i=1}^m \frac{1}{\sqrt{2 \pi }\sigma} \exp \left(-\frac{\left(y_i-\left(\omega X_i+b\right)\right)^2}{2 \sigma^2}\right) L(w)=Πi=1m2πσ1exp(−2σ2(yi−(ωXi+b))2) -
为了方便计算,转化为对数似然:
log L ( w ) = log Π i = 1 m 1 2 π σ exp ( − ( y i − ( ω X i + b ) ) 2 2 σ 2 ) \log L(w)=\log \Pi_{i=1}^m \frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{\left(y_i-\left(\omega X_i+b\right)\right)^2}{2 \sigma^2}\right) logL(w)=logΠi=1m2πσ1exp(−2σ2(yi−(ωXi+b))2)
-
展开化简:
l ( ω ) = log Π i = 1 m 1 2 π σ exp ( − ( y i − ( ω X i + b ) ) 2 2 σ 2 ) = ∑ i = 1 m log 1 2 π σ exp ( − ( y i − ( ω X i + b ) ) 2 2 σ 2 ) = ∑ i = 1 m log 1 2 π σ + ∑ i = 1 m log ( exp ( − ( y i − ( ω X i + b ) ) 2 2 σ 2 ) ) = m log 1 2 π σ − ∑ i = 1 m ( y i − ( ω X i + b ) ) 2 2 σ 2 = m log 1 2 π σ − 1 σ 2 1 2 ∑ i = 1 m ( y i − ( ω X i + b ) ) 2 \begin{align*} l(\omega) & = \log \Pi_{i=1}^m \frac{1}{\sqrt{2 \pi }\sigma} \exp \left(-\frac{\left(y_i-\left(\omega X_i+b\right)\right)^2}{2 \sigma^2}\right)\\[2ex] &=\sum_{i=1}^{m}\log \frac{1}{\sqrt{2 \pi }\sigma}\exp \left(-\frac{\left(y_i-\left(\omega X_i+b\right)\right)^2}{2 \sigma^2}\right)\\[2ex] &=\sum_{i=1}^{m}\log \frac{1}{\sqrt{2 \pi }\sigma}+\sum_{i=1}^{m}\log\left(\exp \left(-\frac{\left(y_i-\left(\omega X_i+b\right)\right)^2}{2 \sigma^2}\right)\right)\\[2ex] &=m\log \frac{1}{\sqrt{2\pi \sigma}}-\sum_{i=1}^{m}\frac{(y_i-(\omega X_i+b))^2}{2 \sigma^2}\\[2ex] &=m\log \frac{1}{\sqrt{2\pi \sigma}}-\frac{1}{\sigma ^2}\frac{1}{2}\sum_{i=1}^{m}(y_i-(\omega X_i+b))^2 \end{align*} l(ω)=logΠi=1m2πσ1exp(−2σ2(yi−(ωXi+b))2)=i=1∑mlog2πσ1exp(−2σ2(yi−(ωXi+b))2)=i=1∑mlog2πσ1+i=1∑mlog(exp(−2σ2(yi−(ωXi+b))2))=mlog2πσ1−i=1∑m2σ2(yi−(ωXi+b))2=mlog2πσ1−σ2121i=1∑m(yi−(ωXi+b))2 -
根据极大似然估计的思想,目标函数为:
J ( ω ) = ∑ i = 1 m ( y i − ( ω X i + b ) ) 2 J(\omega)=\sum_{i=1}^{m}(y_i-(\omega X_i+b))^2 J(ω)=i=1∑m(yi−(ωXi+b))2
此损失函数,又称为最小二乘损失函数。因此现在目标变化为求得 ω \omega ω 和 b b b 使我们的目标函数最小化。
1.2 多元线性回归
- 多元线性回归,因为需要考虑两个或两个以上的自变量,我们的假设(Hypothesis)方程可以表示为:
h θ ( X ) = θ 0 + θ 1 x 1 + θ 2 x 2 + . . . . . . h_\theta (X)=\theta_0+\theta_1x_1+\theta_2x_2+...... hθ(X)=θ0+θ1x1+θ2x2+......
- 为了表示方便我们定义一个额外的变量 X 0 = 1 X_0=1 X0=1 此 X 0 X_0 X0 是一个 n + 1 n+1 n+1 维的向量:
h θ ( X ) = 1 2 ∑ i = 0 n θ i x i = θ T X h_\theta (X)=\frac{1}{2}\sum_{i=0}^{n}\theta_i x_i=\theta^T X hθ(X)=21i=0∑nθixi=θTX
- 因此我们的目标函数可以表示为:
J ( θ ) = 1 2 ∑ i = 0 m ( θ T x i − y i ) 2 = 1 2 ( X θ − y ) T ( X θ − y ) J(\theta)=\frac{1}{2}\sum_{i=0}^{m}(\theta ^T x_i-y_i)^2=\frac{1}{2}(X\theta-y)^T(X\theta-y) J(θ)=21i=0∑m(θTxi−yi)2=21(Xθ−y)T(Xθ−y)
2 线性回归算法优化
2.1 求解多元回归的系数
- 正规方程
最小二乘法 - 梯度下降
- 批量梯度下降 Batch Gradient Descent,BGD
每更新一次权重需要对所有的数据样本点进行遍历。在最小化损失函数的过程中,需要不断的反复地更新权重使得误差函数减小;
特点是每一次参数的更新都用到了所有的训练数据,因此BGD优化方法会非常耗时,且样本数据量越大,训练速度也会变得越慢。 - 随机梯度下降 Stochastic Gradient Descent, SGD
解决BGD训练速度过慢的问题随机选取每个样本的损失函数对目标函数变量求偏导,得到对应的梯度来更新目标函数变量。
因为随机梯度下降是随机选择一个样本进行选代更新一次,所以SGD伴随噪音较BGD要多使得SGD并不是每次迭代都向着整体优化方向。 - 小批量梯度下降 Mini-Batch Gradient Descent,MBGD
避免BGD和SGD的缺点,算法训练过程较快,也保证最终参数训练的准确率。通过增加每次迭代个数来实现的,相当于一个Batch通过矩阵运算,每一个batch上优化参数不会比单个数据慢太多。但每次使用一个batch可大大减小收敛所需要的迭代次数,同时可以使收敛到的结果更接近梯度下降的效果。
- 批量梯度下降 Batch Gradient Descent,BGD
2.2 过拟合问题解决方法
建立的线性回归模型虽然在训练集上表现得很好,但是在测试集中表现得恰好相反,同样在测试集上的损失函数会表现得很大。为了解决过拟合,我们引入了正则项。
- L1正则化是指权值向量中各个元素的绝对值之和,通常表示为:
J ( q ) = ∑ i = 0 m ( h q ( x ( i ) ) − y ( i ) ) 2 + l ∑ j = 1 n ∣ q j ∣ ( l > 0 ) J(q)=\sum_{i=0}^{m}(h_q(x^{(i)})-y^{(i)})^2+l\sum_{j=1}^{n}|q_j| \quad (l>0) J(q)=i=0∑m(hq(x(i))−y(i))2+lj=1∑n∣qj∣(l>0)
- L2正则化是指权值向量中各个元素的平方和,通常表示为:
J ( θ ) = ∑ i = 0 m ( h θ ( x ( i ) ) − y ( i ) ) 2 + λ ∑ j = 1 n θ j 2 ( λ > 0 ) J(\theta)=\sum_{i=0}^{m}(h_\theta(x^{(i)})-y^{(i)})^2+\lambda\sum_{j=1}^{n}\theta_j^2 \quad (\lambda>0) J(θ)=i=0∑m(hθ(x(i))−y(i))2+λj=1∑nθj2(λ>0)
2.3 线性回归的模型评估方法
- 均方误差MSE(Mean Squared Error):均方误差是指所有观测值和预测值之间的平方和的平均数,它反映了模型预测误差的大小。MSE越小,说明模型拟合效果越好。
M S E = 1 m ∑ i = 1 m ( y i − y ^ i ) 2 MSE=\frac{1}{m}\sum_{i=1}^{m}(y_i-\hat{y}_i)^2 MSE=m1i=1∑m(yi−y^i)2
- 均方根误差RMSE(Root Mean Squarde Error)
R M S E = 1 m ∑ i = 1 m ( y i − y ^ i ) 2 RMSE=\sqrt{\frac{1}{m}\sum_{i=1}^{m}(y_i-\hat{y}_i)^2} RMSE=m1i=1∑m(yi−y^i)2
- 平均绝对误差MAE(Mean Absolute Error)
M A E = 1 m ∑ i = 1 m ∣ y i − y ^ i ∣ MAE=\frac{1}{m}\sum_{i=1}^{m}|y_i-\hat{y}_i| MAE=m1i=1∑m∣yi−y^i∣
- R 2 R^2 R2
R 2 = S S R S S T = ∑ ( y ^ i − y ‾ ) 2 ∑ ( y i − y ‾ ) 2 R^2=\frac{SSR}{SST}=\frac{\sum(\hat{y}_i-\overline{y})^2}{\sum(y_i-\overline{y})^2} R2=SSTSSR=∑(yi−y)2∑(y^i−y)2
3 线性回归代码实现
3.1 一元线性回归Python底层实现
# 一元线性回归的实现#导入matplotlib库,主要用于可视化
import matplotlib.pyplot as plt
%matplotlib inline#引入本地字体文件,否则中文会有乱码
#font_set = FontProperties(fname=r"./work/ simsun.ttc", size=12)
from matplotlib.font_manager import FontProperties
import numpy as np# 构造用于训练的数据集
x_train = [4,8,5,10,12]
y_train = [20,50,30,70,60]# 画图函数
def draw(x_train,y_train):plt.scatter(x_train, y_train)# 定义函数求得斜率w和截距b
# 使用最小二乘法对斜率和截距求导并使得导数值等于0求解出斜率和截距
def fit(x_train,y_train): size = len(x_train)numerator = 0 #初始化分子denominator = 0#初始化分母for i in range(size):numerator += (x_train[i]-np.mean(x_train))*(y_train[i]-np.mean(y_train)) denominator += (x_train[i]-np.mean(x_train))**2w = numerator/denominatorb = np.mean(y_train)-w*np.mean(x_train)return w,b#根据斜率w和截距b,输入x计算输出值
def predict(x,w,b): #预测模型y = w*x+breturn y# 根据W,B画图
def fit_line(w,b):
#测试集进行测试,并作图x = np.linspace(4,15,9) #linspace 创建等差数列的函数 #numpy.limspace(start,stop,num,endpoint=True,retstep=False,dtype=None,axis=0#) y = w*x+bplt.plot(x,y)plt.show()if __name__ =="__main__":draw(x_train,y_train)w,b = fit(x_train,y_train)print(w,b) #输出斜率和截距
fit_line(w,b) #绘制预测函数图像
3.2 多元线性回归的实现
# 多元线性回归的实现
# 导入模块
import numpy as np
import pandas as pd# 构造数据,前三列表示自变量X,最后一列表示因变量Y
data = np.array([[3,2,9,20],[4,10,2,72],[3,4,9,21],[12,3,4,20]])
print("data:",data,"\n")X=data[:,:-1]
Y=data[:,-1]X=np.mat(np.c_[np.ones(X.shape[0]),X])# 为系数矩阵增加常数项系数
Y=np.mat(Y)# 数组转化为矩阵print("X:",X,"\n")
print("Y:",Y,"\n")# 根据最小二乘法的目标函数求导为0得到最优参数向量B的解析解公式如下,可以直接求取最优参数向量
B=np.linalg.inv(X.T*X)*(X.T)*(Y.T)
print("B:",B,"\n")# 输出系数,第一项为常数项,其他为回归系数
print("1,60,60,60预测结果:",np.mat([1,60,60,60])*B,"\n")#预测结果# 相关系数
Q_e=0
Q_E=0
Y_mean=np.mean(Y)
for i in range(Y.size):Q_e+=pow(np.array((Y.T)[i]-X[i]*B),2)Q_E+=pow(np.array(X[i]*B)-Y_mean,2)
R2=Q_E/(Q_e+Q_E)
print("R2",R2)3.3 线性回归第三方库实现
# 导入sklearn下的LinearRegression 方法
from sklearn.linear_model import LinearRegression
import numpy as np
model = LinearRegression()# 构造用于训练的数据集
x_train = np.array([[2,4],[5,8],[5,9],[7,10],[9,12]])
y_train = np.array([20,50,30,70,60])# 训练模型并输出模型系数和训练结果
model.fit(x_train,y_train)
#fit(x,y,sample_weight=None)x:训练集 y:目标值 sample_weight:每个样本的个数
#coef_ 系数w,intercept_截距
print(model.coef_) #输出系数w
print(model.intercept_) #输出截距b
print(model.score(x_train,y_train)) #输出模型的评估分数R2
Reference
- [1] https://connect.huaweicloud.com/courses/learn/Learning/sp:cloudEdu_?courseNo=course-v1:HuaweiX+CBUCNXE086+Self-paced&courseType=1
- [2] https://authoring-modelarts-cnnorth4.huaweicloud.com/console/lab?share-url-b64=aHR0cHM6Ly9tb2RlbGFydHMtbGFicy1iajQtdjIub2JzLmNuLW5vcnRoLTQubXlodWF3ZWljbG91ZC5jb20vY291cnNlL2h3Y19lZHUvbWFjaGluZV9sZWFybmluZy9mb3JfaHdjX2VkdS9MaW5lYXJfUmVncmVzc2lvbl9od2NfZWR1LmlweW5i
—— END ——
如果以上内容有任何错误或者不准确的地方,欢迎在下面 👇 留言。或者你有更好的想法,欢迎一起交流学习~~~
更多精彩内容请前往 AXYZdong的博客
相关文章:
)
机器学习丨2. 线性回归(Linear Regression)
Author:AXYZdong 硕士在读 工科男 有一点思考,有一点想法,有一点理性! 定个小小目标,努力成为习惯!在最美的年华遇见更好的自己! CSDNAXYZdong,CSDN首发,AXYZdong原创 唯…...
python+django企业员工考勤打卡信息管理系统66lgr
本员工信息管理系统以Django作为框架,Python语言,B/S模式以及MySql作为后台运行的数据库。本系统主要包括以下功能模块:员工、部门、员工合同、考勤信息、打卡信息、员工工资等模块。 本文着重阐述了员工信息管理系统的分析、设计与实现&…...

【Java Web】论坛帖子添加评论
数据层 增加评论数据;修改帖子评论数量; 业务层 处理添加评论的业务;先增加评论、在更新帖子的评论数量; 表现层 处理添加评论数据的请求;设置添加评论的表单。 一、数据层 1.1 CommentMapper.java package com.no…...

如何建设一个安全运营中心(SOC)?
然信息安全管理问题主要是个从上而下的问题,不能指望通过某一种工具来解决,但良好的安全技术基础架构能有效的推动和保障信息安全管理。随着国内行业IT应用度和信息安全管理水平的不断提高,企业对于安全管理的配套设施如安全运营中心…...

如何以Base64形式存储、返回图片数据
在Java中,可以使用Base64类来将图片转换为Base64编码。下面是一个示例代码: Java代码直接处理: import java.io.File; import java.io.FileInputStream; import java.io.IOException; import java.util.Base64; public class ImageToBase64…...

【大模型】自动化问答生成:使用GPT-3.5将文档转化为问答对
自动化问答生成:使用GPT-3.5将文档转化为问答对 正文步骤1:准备工作步骤2:编写Python脚本 总结 当我们需要将大段文档转化为问答对时,OpenAI的GPT-3.5模型提供了一个强大的工具。这个教程将向您展示如何编写一个Python脚本&#x…...
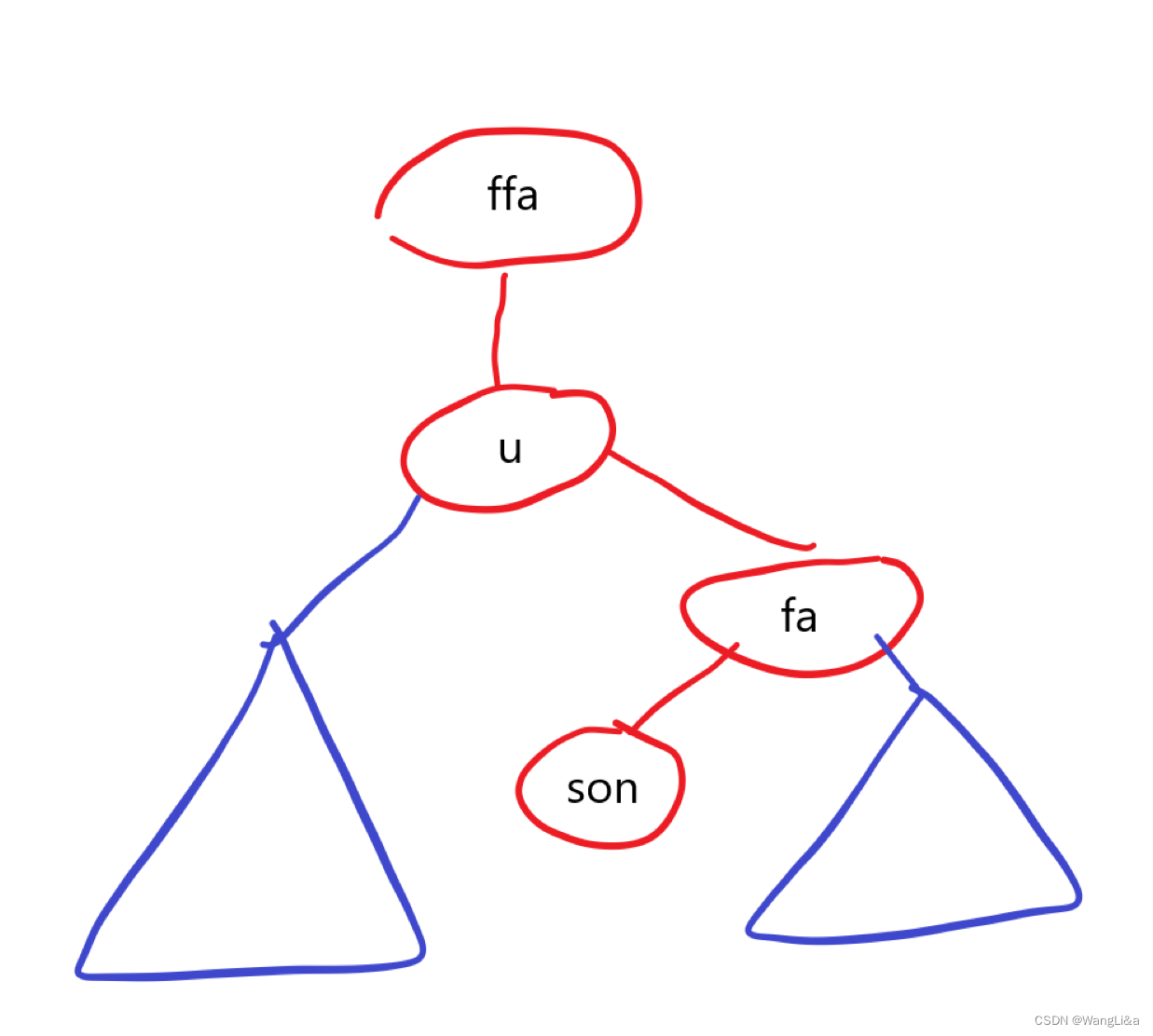
普通平衡树 Splay
Splay 简介 Splay(伸展树),又叫做分裂树,是一种自调整形式的二叉查找树,满足二叉查找树的性质:一个节点左子树的所有节点的权值,均小于这个节点的权值。且其右子树所有节点的权值,均…...

复旦-华盛顿EMBA:走近亿咖通科技,探寻汽车智能化的科创“密码”
6月20日,应复旦大学-华盛顿大学EMBA项目18班校友周靖的邀请,项目校友参访了科创企业ECARX亿咖通科技。作为该公司资深副总裁、中国首席财务官,周靖带领大家通过产品演示、实车驾驶和交流对话探寻汽车智能化的科创“密码”,近距离感…...

学习心得07:C#
之前也没有看过C#的书,C#的程序倒是搞了一些。好在项目不大,我又会套路。 C#很象是JAVA。好像就是JAVA出来之后,微软抄的。好东西就要学习,这不丢脸。 我倒是想,有没有办法把JAVA和C#进行映射,然后直接编译…...

importlib的使用、9个视图子类、视图集、drf之路由、drf之请求响应回顾、GenericViewSet相关流程图
一 drf之请求响应回顾 # 1 drf请求-请求对象:data,query_params,其他跟之前一样,FILES-默认:支持三种编码-局部配置:视图类中-from rest_framework.parsers import JSONParser, FormParser, MultiPartPars…...

国际站阿里云服务器远程桌面密码错误怎么办?苹果手机如何远程登录?
阿里云服务器是云计算领域的一种重要服务,它可以帮助用户在云端部署和管理自己的应用程序和网站。但是,有时候用户可能会遇到远程桌面密码错误的问题,导致无法登录到服务器。本文将介绍一些解决办法,以及如何使用苹果手机远程登录…...
CRMEB多端多语言系统文件上传0Day代审历程
Git仓库: https://github.com/crmeb/CRMEB简介: 两天攻防中,某政局子公司官网后台采用的CRMEB开源商城CMS,挺奇葩,别问怎么总让我碰到这种东西,我也不知道,主打的就是一个魔幻、抽象。最后通过…...
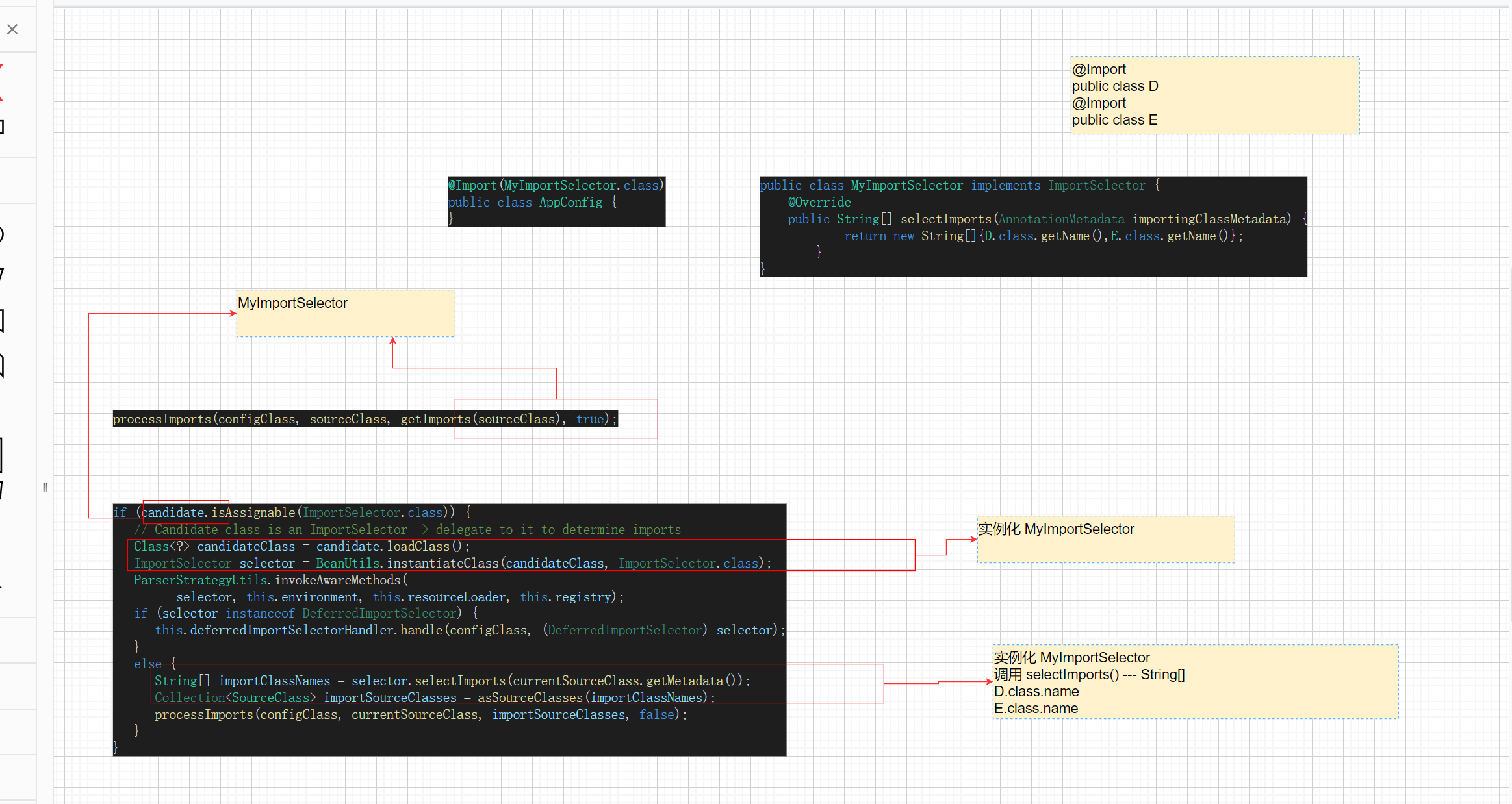
孙哥Spring源码第18集
第18集 refresh()-invokeBeanFactoryPostProcessor-二-ConfigurationClassPostProcessor的处理逻辑 【视频来源于:B站up主孙帅suns Spring源码视频】【微信号:suns45】 1、为什么PropertySource先处理? 因为Conponent A在处理的过程中 要把…...

【STM32】文件系统FATFS与Flash的初步使用
文件系统简介 简介可以不看,直接看移植步骤 文件系统是介于应用层和底层间的模糊层。底层提供API,比如说使用SDIO或者SPI等读写一个字节。文件系统把这些API组合包装起来,并且提供一些列函数,我们可以使用这些函数进行更进一步的…...
Android Glide in RecyclerView,only load visible item when page return,Kotlin
Android Glide in RecyclerView,only load visible item when page return,Kotlin base on this article: Android Glide preload RecyclerView切入后台不可见再切换可见只加载当前视野可见区域item图片,Kotlin_zhangphil的博客…...

【SCI征稿】3个月左右录用!计算机信息技术等领域均可,如机器学习、遥感技术、人工智能、物联网、人工神经网络、数据挖掘、图像处理
计算机技术类SCIE&EI 【期刊简介】IF:1.0-2.0,JCR4区,中科院4区 【检索情况】SCIE&EI 双检,正刊 【参考周期】期刊部系统内提交,录用周期3个月左右,走完期刊部流程上线 【征稿领域】计算机信息…...

Golang 中的 crypto/ecdh 包详解
什么是 ECDH 算法? ECDH(Elliptic Curve Diffie-Hellman)算法是一种基于椭圆曲线的密钥交换协议,用于安全地协商共享密钥(Secret Key),步骤如下: 1. 选择椭圆曲线:ECDH…...

系统学习live555
文章目录 系统学习live555系统学习LIVE555的步骤:1.了解基本概念:2.**查看官方文档:**3.**下载和编译库:**4.**阅读示例代码:**5.**了解库结构:**6.**创建简单项目:**7.**阅读更多文档ÿ…...
Linux下的系统编程——进程的执行与回收(八)
前言: 前面我们对进程已经有了一个初步的了解与认识,现在让我们学习一下进程中一些函数的具体使用,比如exec可以执行一些指定的程序,wait / waitpid可以回收子进程,什么是孤儿进程,什么是僵尸进程…...

第十九章 ObjectScript - 执行例程
文章目录 第十九章 ObjectScript - 执行例程执行例程New 命令 第十九章 ObjectScript - 执行例程 执行例程 执行例程时,使用DO命令,如下所示: do ^routinename要执行一个过程、函数或子程序(不访问其返回值),可以使用以下命令: do label^ro…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...
