数学建模之插值法
目录
- 1 插值法概述
- 2 插值法原理
- 3 拉格朗日插值
- 4 牛顿插值
- 5 三次Hermite插值(重点)
- 6 三次样条插值(重点)
- 7 各种插值法总结
- 8 n 维数据的插值
- 9 插值法拓展
- 10 课后作业
1 插值法概述
数模比赛中,常常需要根据已知的函数点进行数据、模型的处理和分析,而有时候现有的数据是极少的,不足以支撑分析的进行,这时就需要使用一些数学的方法,“模拟产生”一些新的但又比较靠谱的值来满足需求,这就是插值的作用。
那什么是插值法?

插值法又可以分为以下三类:

❗️ 注意:
- 针对于建模比赛,我们一般只讨论多项式插值和分段插值,三角插值一般要用到傅里叶变换等复杂的数学工具。
2 插值法原理
一维插值 问题:
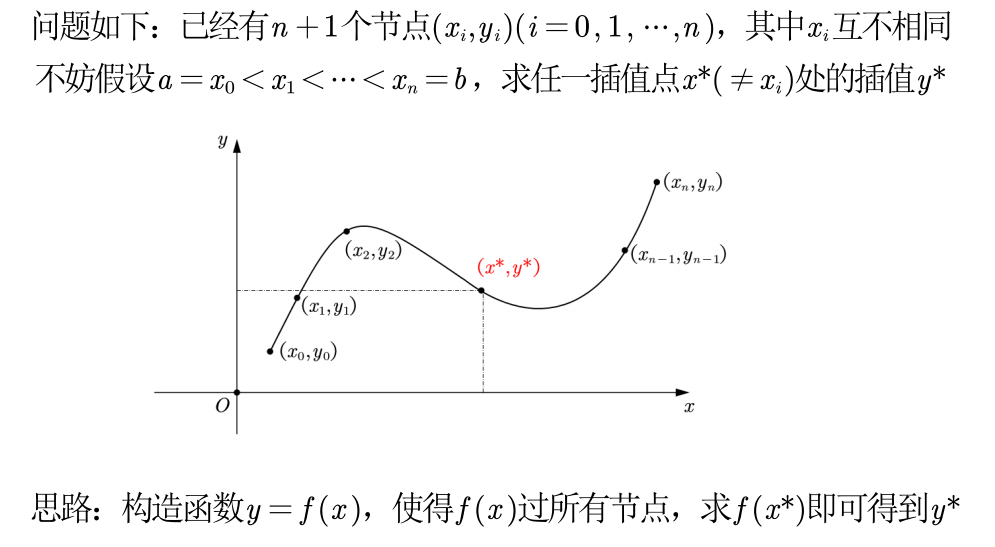

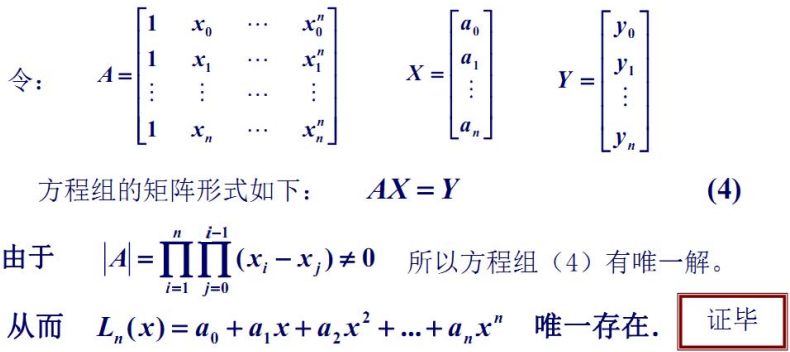
❗️ 注意:
- 只要 n+1 个节点互异,满足上述插值条件的多项式是唯一的
- 如果不限制多项式的次数,插值多项式并不唯一
3 拉格朗日插值
在数值分析中,拉格朗日插值法是以法国十八世纪数学家约瑟夫∙路易斯∙拉格朗日命名的一种多项式插值方法。在若干个不同的地方得到相应的观测值,拉格朗日插值法可以找到一个多项式,其恰好在各个观测的点取到观测到的值。
😋 举例:
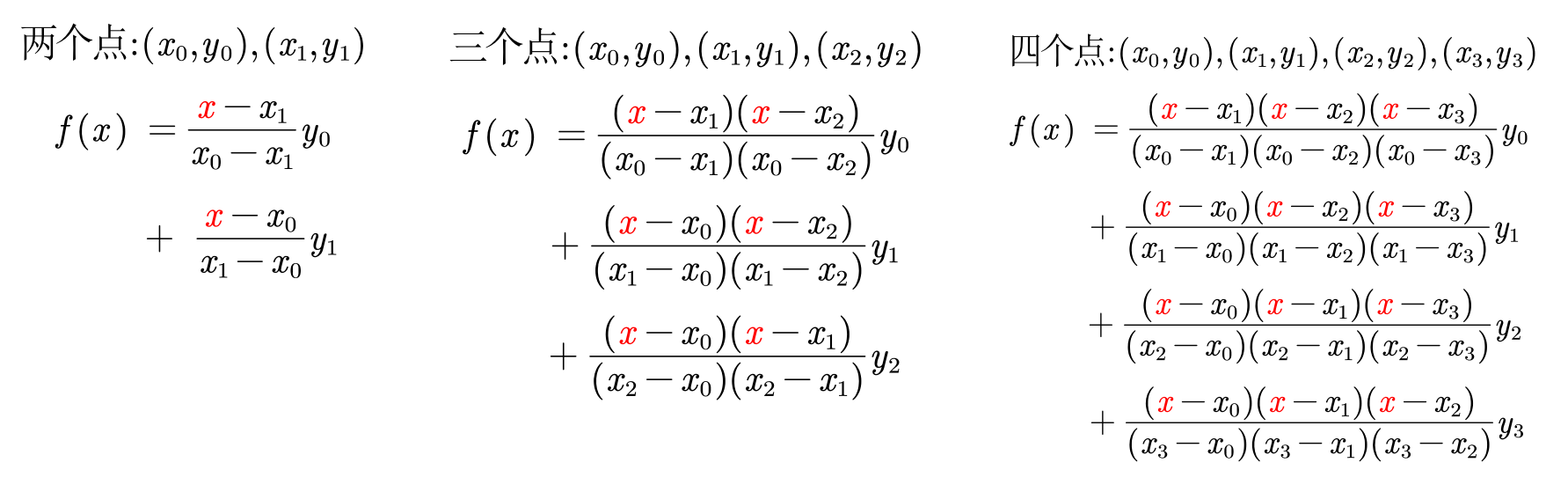
由上述简单的例子可得,拉格朗日插值多项式:

但是使用拉格朗日插值有个很大的缺点:龙格现象(Runge phenomenon)
- 高次插值会产生龙格现象,即在两端处波动极大,产生明显的震荡。在不熟悉曲线运动趋势的前提下,不要轻易使用高次插值。
😋 举例:

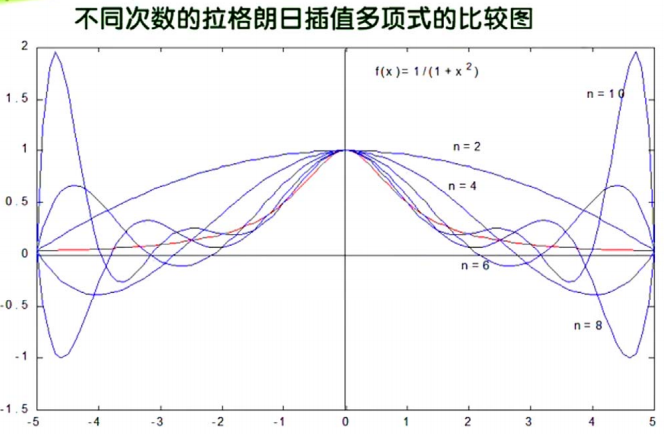
我们已经知道了
- 插值多项式次数高精度未必显著提高
- 插值多项式次数越高摄入的误差可能显著增大
那么如何提高插值精度?—— 采用 分段低次插值

4 牛顿插值

与拉格朗日插值的对比:



❗️注意:
- 所以我们几乎不用拉格朗日插值和牛顿插值,更多的是用下面介绍的埃尔米特(Hermite)插值以及三次样条插值
5 三次Hermite插值(重点)
不但要求在节点上的函数值相等,而且还要求对应的导数值也相等,甚至要求高阶导数也相等,满足这种要求的插值多项式就是 Hermite 插值多项式。

直接使用 Hermite 插值得到的多项式次数较高,也存在着龙格现象,因此在实际应用中,往往使用分段三次 Hermite 插值多项式 (PCHIP)

6 三次样条插值(重点)



7 各种插值法总结
由于拉格朗日插值和牛顿插值仅仅要求插值多项式在插值节点处与被插函数有相等的函数值,而这种插值多项式却不能全面反映被插值函数的性态,我们一般不用。
三次Hermite插值与样条插值结果对比
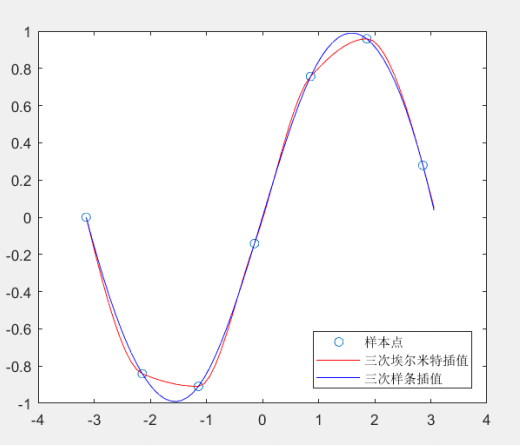
可以看出,三次样条生成的曲线更加光滑。在实际建模中,由于我们不知道数据的生成过程,因此这两种插值都可以使用。
8 n 维数据的插值

9 插值法拓展
以上插值算法也可用于短期预测
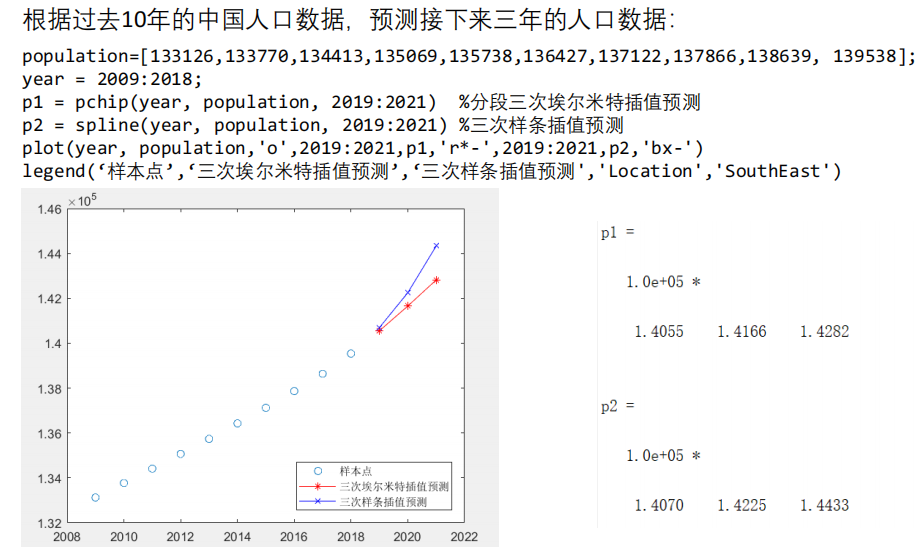
❗️注意:
- 实际建模过程中,大家尽量不要用插值算法来预测,上面只是给大家举的一个小例子;如果要预测,可以选择拟合算法,也可以使用之后要学的专门用于预测的算法。
10 课后作业
建模实例:MathorCup 第六届A题 淡水养殖池塘水华发生及池水净化处理
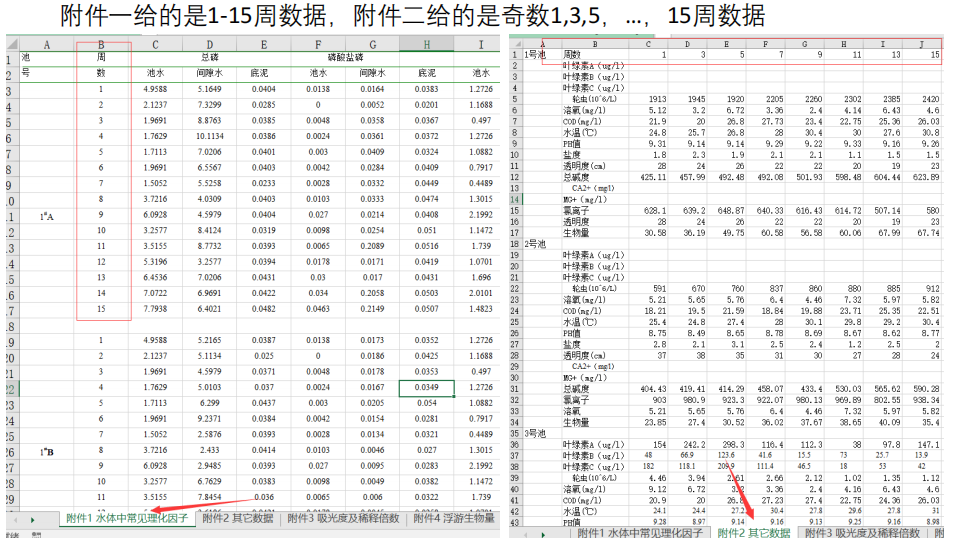
华中农业大学特等奖文章

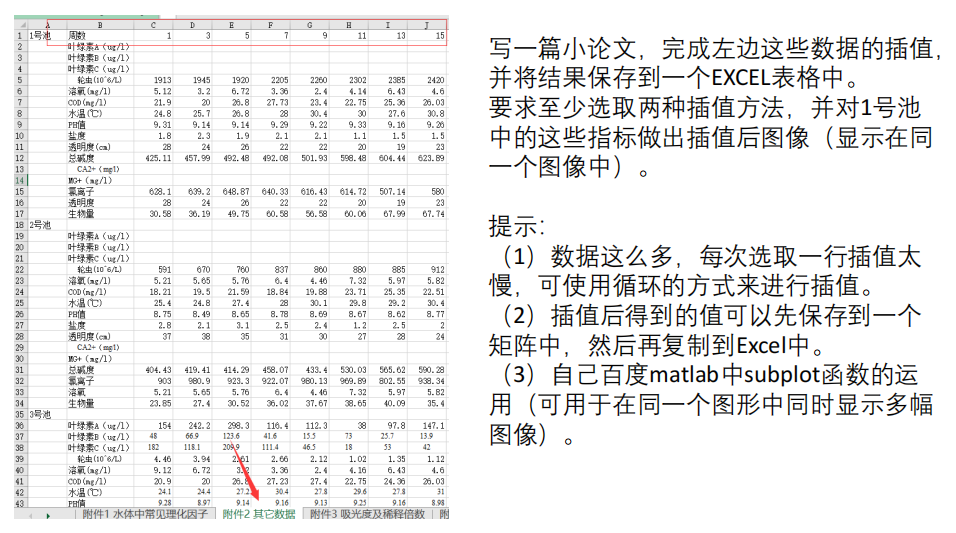
参考答案:
相关文章:

数学建模之插值法
目录 1 插值法概述2 插值法原理3 拉格朗日插值4 牛顿插值5 三次Hermite插值(重点)6 三次样条插值(重点)7 各种插值法总结8 n 维数据的插值9 插值法拓展10 课后作业 1 插值法概述 数模比赛中,常常需要根据已知的函数点进…...

rhcsa学习2(vim、创建管理用户、组等)
创建、查看和编辑文本文件 重定向符号 > 进程使用称为文件描述符的编号通道来获取输入并发送输出。所有进程在开始时至少要有三个文件描述符。如果程序打开连接至其他文件的单独连接,则可能要使用更大编号的文件描述符 上述通过通道1去写入,且写入的文…...
)
【使用教程】Github(自用)
1.下载Git⼯具 使在windows 命令⾏下边可以输⼊这两个命令: gitssh-keygen 2.配置git信息: 在命令⾏⾥输⼊: $ git config --global user.name “你在Github上注册的账号” $ git config --global user.email 你在Github上注册的邮箱 3. c…...
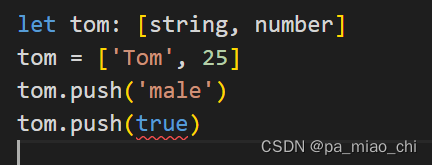
typeScript学习笔记(一)
学习资源来自: 类与接口 TypeScript 入门教程 (xcatliu.com) 一.TypeScript的安装和运行 1.安装TypeScript 通过npm(Node.js包管理器)安装Visual Studio的TypeScript插件:(Visual Studio 2017和Visual Studio 2015 Update 3默认包含了Ty…...

第4章:网络层
文章目录 一、概述和功能2.SDN二、转发1.IP数据报(1)IP数据报的首部字段(2)IP数据报的分片2.IPv4地址:<网络号>,<主机号>3.IP编址 (三个历史阶段)(1)分类IP地址①特殊IP地址②私有IP地址③网络地址转换NAT:导致IP地址变化MAC地址、IP地址变化问题(2)子网划分与子…...

C高级day1 shell 指令的补充学习
使用cut截取出Ubuntu用户的家目录,要求:不能使用":"作为分割 2.思维导图...

灰度变换与空间滤波
灰度变换与空间滤波 背景知识 空间域指包含图像像素的平面,灰度变换与空间滤波均在空间域进行,即直接在图像像素上操作,表示为 g ( x , y ) T [ f ( x , y ) ] g(x,y)T[f(x,y)] g(x,y)T[f(x,y)] ,其中 T T T 是在点 ( x , y…...
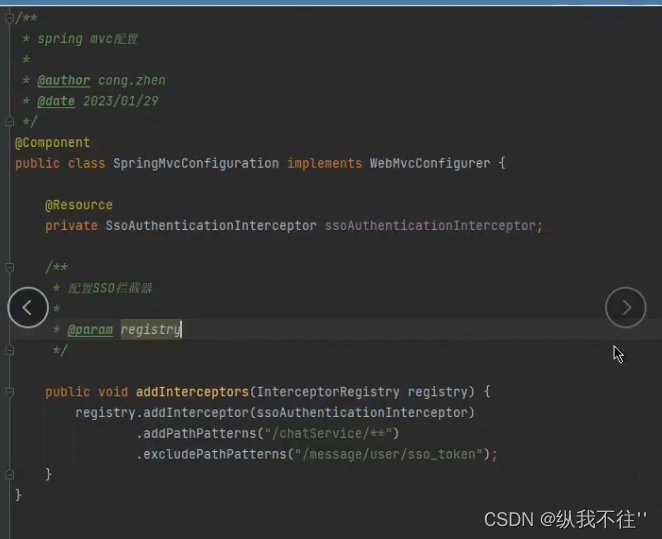
敏感接口权限校验
前端校验 (从前端或者从token里面拿一下),看一下用户有没有这个页面的权限(但是一般不用,因为nodejs也可以写后端,但是放到前端去校验不安全) 后端校验 需要梳理敏感数据接口,将这…...
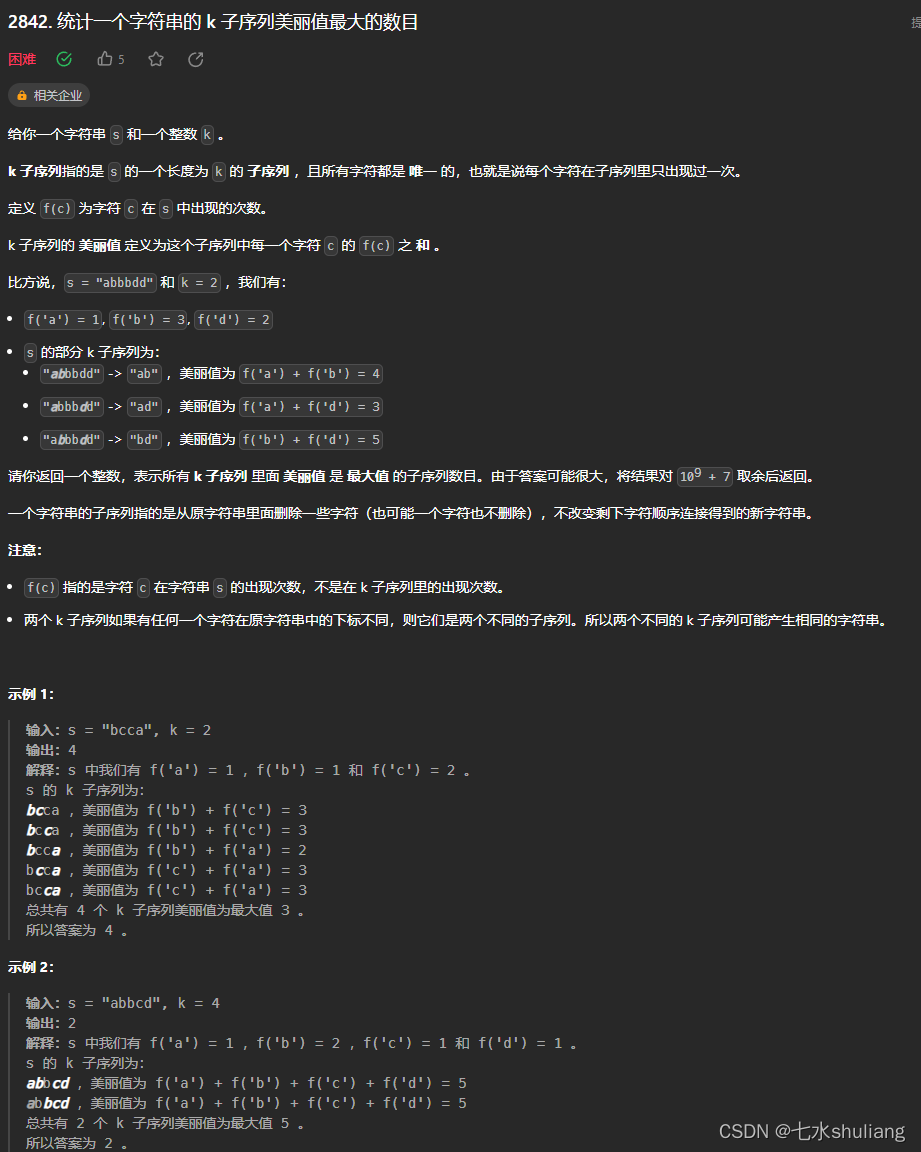
[LeetCode周赛复盘] 第 112场双周赛20230903
[LeetCode周赛复盘] 第 112场双周赛20230903 一、本周周赛总结2839. 判断通过操作能否让字符串相等 I1. 题目描述2. 思路分析3. 代码实现 2840. 判断通过操作能否让字符串相等 II1. 题目描述2. 思路分析3. 代码实现 2841. 几乎唯一子数组的最大和1. 题目描述2. 思路分析3. 代码…...
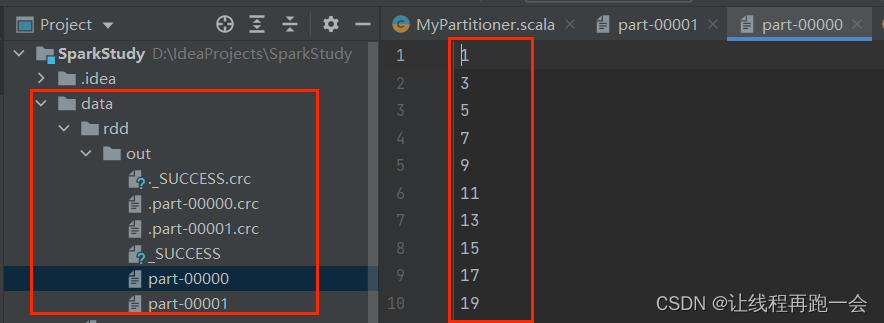
Spark【RDD编程(二)RDD编程基础】
前言 接上午的那一篇,下午我们学习剩下的RDD编程,RDD操作中的剩下的转换操作和行动操作,最好把剩下的RDD编程都学完。 Spark【RDD编程(一)RDD编程基础】 RDD 转换操作 6、distinct 对 RDD 集合内部的元素进行去重…...
【2023最新版】MySQL安装教程
目录 一、MySQL简介 二、MySQL安装 1. 官网 2. 下载 3. 安装 4. 配置环境变量 配置前 配置中 配置后 5. 验证 一、MySQL简介 MySQL是一种开源的关系型数据库管理系统(RDBMS),它被广泛用于存储和管理结构化数据。MySQL提供了强大的功…...

关于mysql数据文件损坏导致的mysql无法启动的问题
环境 rocky linux 9 (跟centos几乎一模一样) myqsl 8.0, 存储引擎使用innodb 问题描述 1. 服务器异常关机,重启启动后发现mysql无法连接,使用命令查看mysql状态: systemctl status mysqld 发现mysql服…...
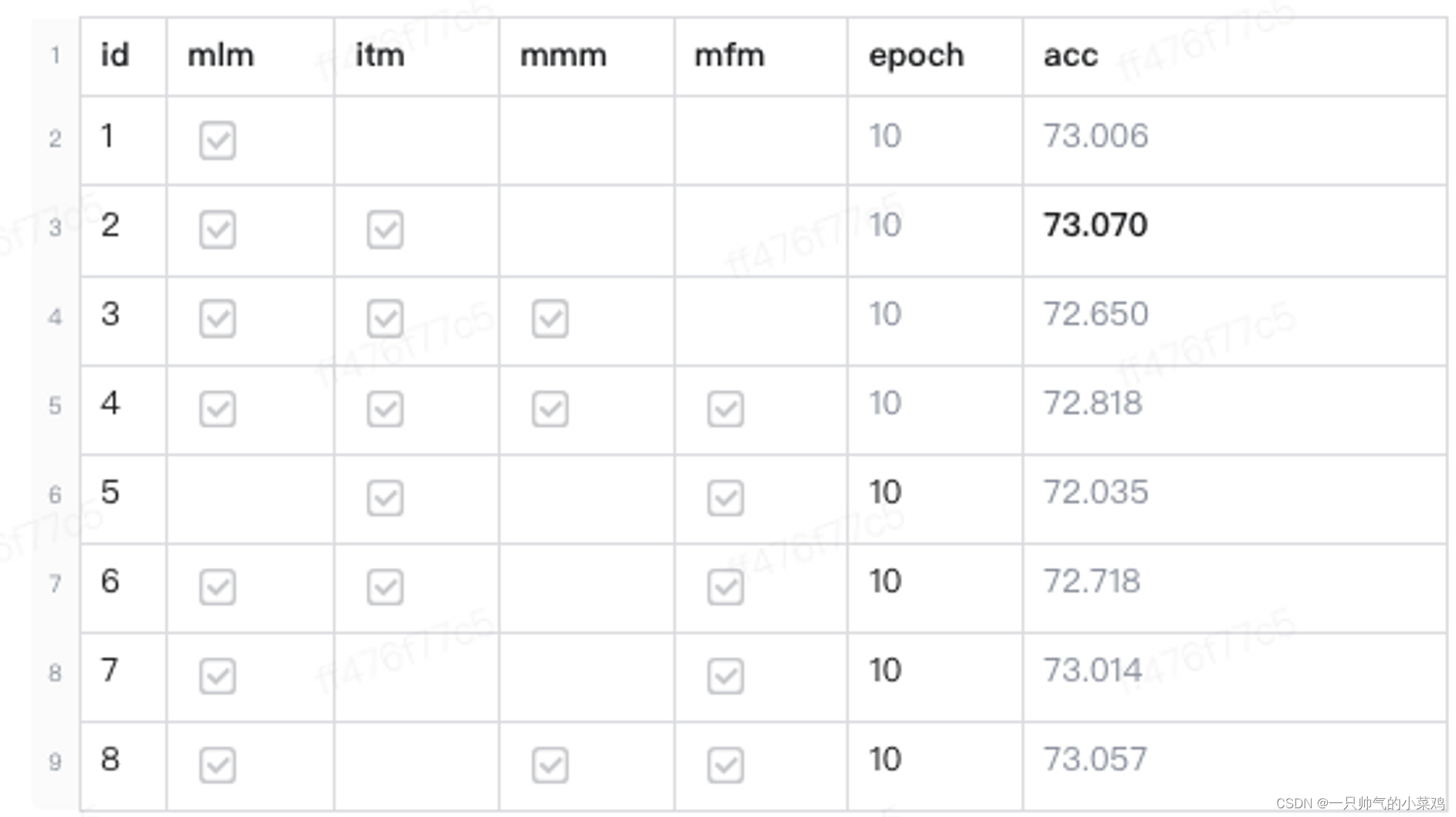
深度学习之视频分类项目小记
写在前面,最近一阵在做视频分类相关的工作,趁有时间来记录一下。本文更注重项目实战与落地,而非重点探讨多模/视频模型结构的魔改 零、背景 目标:通过多模态内容理解技术,构建视频层级分类体系原技术方案:…...
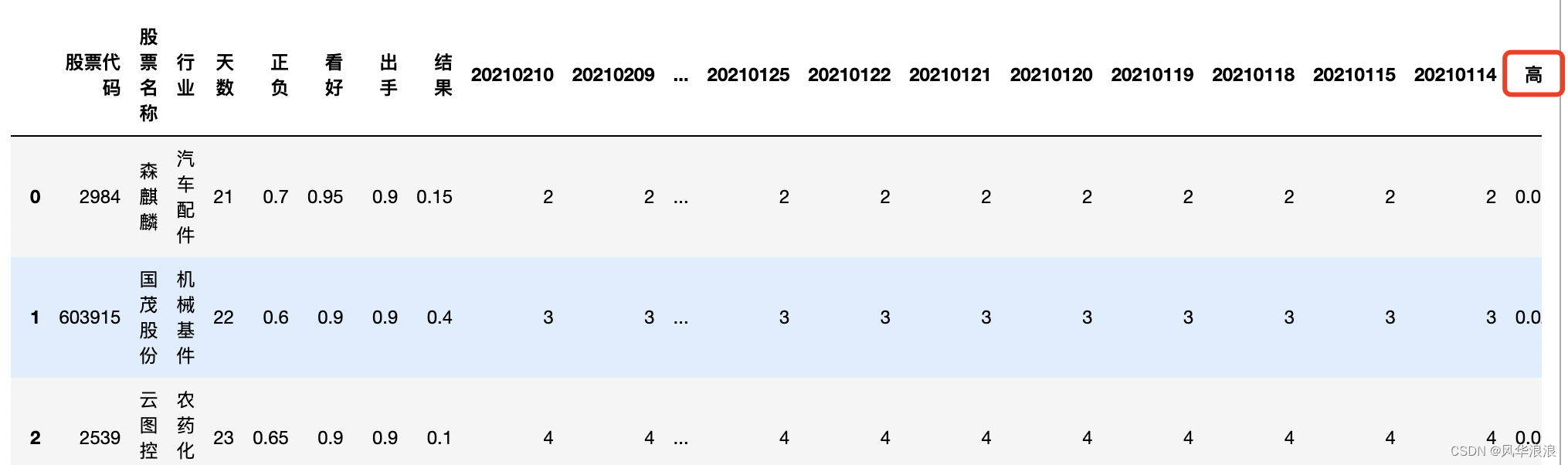
pandas(四十三)Pandas实现复杂Excel的转置合并
一、Pandas实现复杂Excel的转置合并 读取并筛选第一张表 df1 pd.read_excel("第一个表.xlsx") df1# 删除无用列 df1 df1[[股票代码, 高数, 实际2]].copy() df1df1.dtypes股票代码 int64 高数 float64 实际2 int64 dtype: object读取并处理第二张表…...
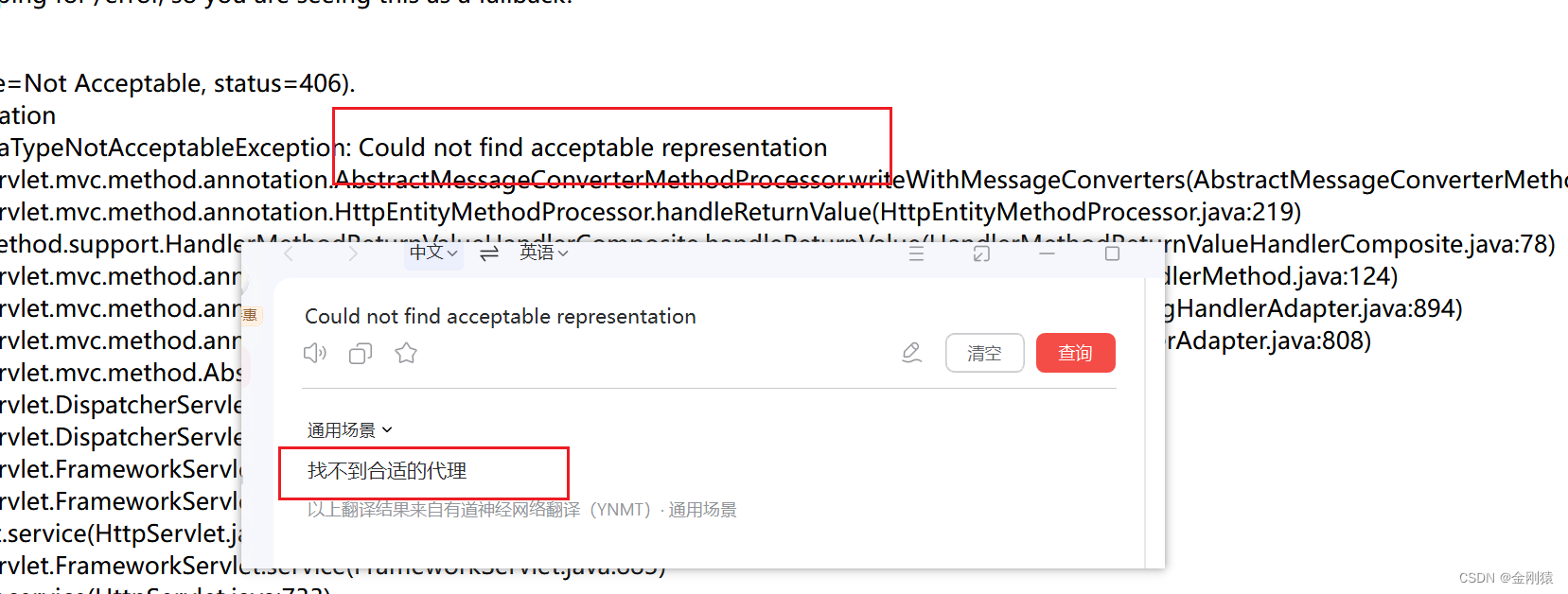
42、springboot 的 路径匹配 和 内容协商
springboot 的 路径匹配 和 内容协商 对于路径匹配,自己的总结就是: 以前路径匹配时默认不检查后缀,http://localhost:8080/aaa.json 可以直接访问到 RequstMapping(“/aaa”) 的方法。现在不行了。现在会检查后缀了。 内容协商的理解总结&…...

一文讲解Linux内核内存管理架构
内存管理子系统可能是linux内核中最为复杂的一个子系统,其支持的功能需求众多,如页面映射、页面分配、页面回收、页面交换、冷热页面、紧急页面、页面碎片管理、页面缓存、页面统计等,而且对性能也有很高的要求。本文从内存管理硬件架构、地址…...

教你如何使用API接口获取数据
随着互联网技术的发展和应用的普及,越来越多的系统和应用提供API接口供其他系统和应用进行数据交互。通过API接口,我们可以获取到各种各样的数据,例如天气预报、股票行情、新闻摘要等等。本文将介绍如何使用API接口获取数据,并附有…...
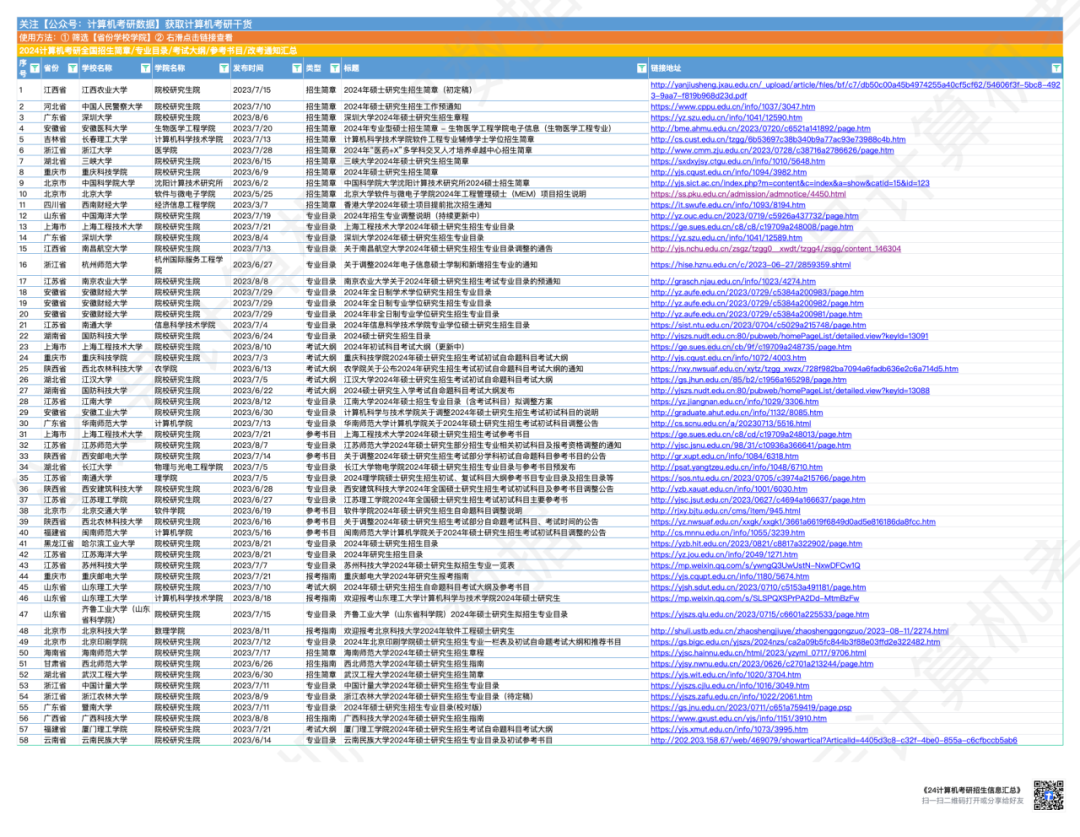
集美大学计算机改考408!福建省全面改考,仅剩一个自命题院校
9月5日,集美大学发布通知,0835软件工程、0854电子信息2024考试科目发生变更!由822数据结构调整为408计算机学科专业基础 https://zsb.jmu.edu.cn/info/1532/4701.htm 直接由一门改为考四门,难度升级不小。 目前福建省内计算机考…...
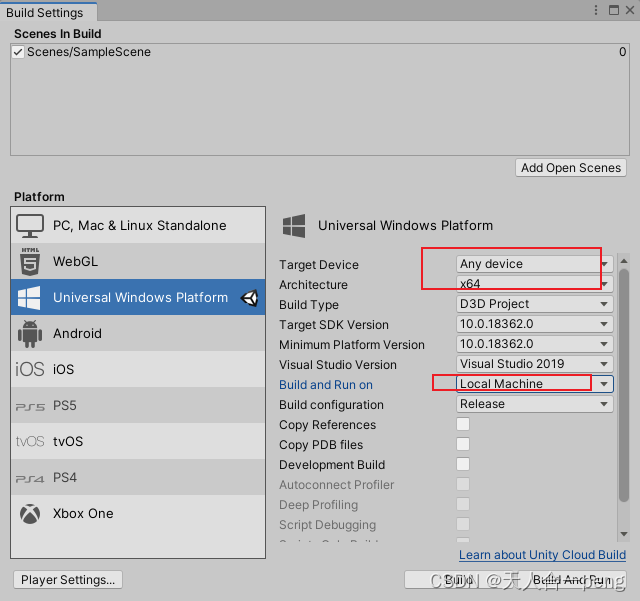
Hololens2部署很慢可能是unity工程选择不对
这样就很快,几分钟就完成了。(虽然又遇到新问题了) 第一次使用时如下,直接运行了一个多小时还没有完...

群论学习记录
群论学习记录 1. 2023.09.07 1. 2023.09.07 群论 (Group Theory) 终极速成 / 物理系零基础火箭级 notes https://zhuanlan.zhihu.com/p/378039151 https://zhuanlan.zhihu.com/p/164653537 群的定义重排定理子群陪集定理:由重排定理可推出1.4-(2&#x…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...
