浙大陈越何钦铭数据结构08-图7 公路村村通【循环和最小堆版】
题目
现有村落间道路的统计数据表中,列出了有可能建设成标准公路的若干条道路的成本,求使每个村落都有公路连通所需要的最低成本。
输入格式:
输入数据包括城镇数目正整数N(≤1000)和候选道路数目M(≤3N);随后的M行对应M条道路,每行给出3个正整数,分别是该条道路直接连通的两个城镇的编号以及该道路改建的预算成本。为简单起见,城镇从1到N编号。
输出格式:
输出村村通需要的最低成本。如果输入数据不足以保证畅通,则输出−1,表示需要建设更多公路。
输入样例:
6 15
1 2 5
1 3 3
1 4 7
1 5 4
1 6 2
2 3 4
2 4 6
2 5 2
2 6 6
3 4 6
3 5 1
3 6 1
4 5 10
4 6 8
5 6 3
输出样例:
12
分析:
一个典型的最小生成树问题,可以用Prim或Kruskal实现,本文使用Prim用循环和最小堆2种方式实现。
循环代码:
#include <stdio.h>
#include <stdlib.h>#define MAX_VERTEX_NUM 1000
#define INFINITY 65535
#define ERROR -1typedef int Vertex;
typedef int WeightType;struct _Edge
{Vertex V, W;WeightType weight;
};
typedef struct _Edge *Edge;typedef struct _AdjNode *AdjNode;
struct _AdjNode
{Vertex adjV;WeightType weight;AdjNode next;
};typedef struct AdjTable
{AdjNode firstEdge;
} AdjTable[MAX_VERTEX_NUM];struct _LGraph
{int Nv, Ne;AdjTable graph;
};
typedef struct _LGraph *LGraph;LGraph CreateGraph(int vertexNum);
void InsertEdge(LGraph graph, Edge E);
LGraph BuildGraph(int vertexNum, int edgeNum);
Vertex FindMinDist(LGraph G, WeightType dist[]);
int Prim(LGraph graph, Vertex S);/*
08-图7 公路村村通
难度:1星6 15
1 2 5
1 3 3
1 4 7
1 5 4
1 6 2
2 3 4
2 4 6
2 5 2
2 6 6
3 4 6
3 5 1
3 6 1
4 5 10
4 6 8
5 6 3126 4
1 2 5
1 3 3
1 4 7
5 6 26 6
1 2 10
2 4 20
3 4 30
1 3 40
1 4 50
2 3 604 4
1 2 10
2 3 20
3 4 30
1 4 404 6
1 2 10
1 3 40
1 4 50
2 3 60
2 4 20
3 4 30
602 1
1 2 107 21
1 2 14
1 3 11
1 4 19
1 5 12
1 6 17
1 7 20
2 3 16
2 4 15
2 5 13
2 6 10
2 7 18
3 4 20
3 5 12
3 6 11
3 7 16
4 5 14
4 6 17
4 7 19
5 6 10
5 7 15
6 7 137 21
1 2 14
1 3 11
1 4 19
1 5 12
1 6 17
1 7 20
2 3 16
2 4 15
2 5 13
2 6 10
2 7 18
3 4 20
3 5 12
3 6 11
3 7 16
4 5 14
4 6 17
4 7 19
5 6 10
5 7 15
6 7 13*/int main()
{int N, M;scanf("%d %d", &N, &M);LGraph G = BuildGraph(N, M);printf("%d\n", Prim(G, 0));free(G);return 0;
}LGraph CreateGraph(int vertexNum)
{LGraph G;G = (LGraph)malloc(sizeof(struct _LGraph));G->Nv = vertexNum;G->Ne = 0;for (int V = 0; V < G->Nv; V++){G->graph[V].firstEdge = NULL;}return G;
}void InsertEdge(LGraph G, Edge E)
{AdjNode NewNode;NewNode = (AdjNode)malloc(sizeof(struct _AdjNode));NewNode->adjV = E->W;NewNode->weight = E->weight;NewNode->next = G->graph[E->V].firstEdge;G->graph[E->V].firstEdge = NewNode;NewNode = (AdjNode)malloc(sizeof(struct _AdjNode));NewNode->adjV = E->V;NewNode->weight = E->weight;NewNode->next = G->graph[E->W].firstEdge;G->graph[E->W].firstEdge = NewNode;
}LGraph BuildGraph(int vertexNum, int edgeNum)
{LGraph G = CreateGraph(vertexNum);G->Ne = edgeNum;Edge E;E = (Edge)malloc(sizeof(struct _Edge));for (int i = 0; i < G->Ne; i++){scanf("%d %d %d", &E->V, &E->W, &E->weight);E->V--;E->W--;InsertEdge(G, E);}free(E);return G;
}Vertex FindMinDist(LGraph G, WeightType dist[])
{ /* 返回未被收录顶点中dist最小者 */Vertex minV, V;WeightType minDist = INFINITY;for (V = 0; V < G->Nv; V++){if (dist[V] != 0 && dist[V] < minDist){/* 若V未被收录,且dist[V]更小 */minDist = dist[V]; /* 更新最小距离 */minV = V; /* 更新对应顶点 */}}if (minDist < INFINITY) /* 若找到最小dist */return minV; /* 返回对应的顶点下标 */elsereturn ERROR; /* 若这样的顶点不存在,返回-1作为标记 */
}int Prim(LGraph G, Vertex S)
{ // 只计算TotalWeight,无需实际创建生成树WeightType dist[G->Nv], totalWeight;Vertex V;AdjNode W;int vCount;for (V = 0; V < G->Nv; V++)dist[V] = INFINITY;for (W = G->graph[S].firstEdge; W; W = W->next)dist[W->adjV] = W->weight;totalWeight = 0;vCount = 0;dist[S] = 0;vCount++;while (1){V = FindMinDist(G, dist);if (V == ERROR)break;totalWeight += dist[V];dist[V] = 0;vCount++;for (W = G->graph[V].firstEdge; W; W = W->next){if (dist[W->adjV] != 0){if (W->weight < dist[W->adjV]){dist[W->adjV] = W->weight;}}}}if (vCount < G->Nv) /* MST中收的顶点少于|V|-1个 */totalWeight = ERROR;return totalWeight;
}
最小堆代码:
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>#define MIN_DATA -1000
#define ELEMENT_TYPE int
#define MAX_VERTEX_NUM 1000
#define INFINITY 65535
#define ERROR -1typedef int Vertex;
typedef int WeightType;struct _MinHeap
{ELEMENT_TYPE *Elements;int Size;int Capacity;
};
typedef struct _MinHeap *MinHeap;struct _Edge
{Vertex V, W;WeightType weight;
};
typedef struct _Edge *Edge;typedef struct _AdjNode *AdjNode;
struct _AdjNode
{Vertex adjV;WeightType weight;AdjNode next;
};typedef struct AdjTable
{AdjNode firstEdge;
} AdjTable[MAX_VERTEX_NUM];struct _LGraph
{int Nv, Ne;AdjTable graph;
};
typedef struct _LGraph *LGraph;MinHeap CreateHeap(int MaxSize);
bool isEmpty(MinHeap H);
bool isFull(MinHeap H);
ELEMENT_TYPE DelMin(MinHeap H, int dist[]);
void BuildMinHeap(MinHeap H, int dist[]);
void PercUp(MinHeap H, int p, int dist[]);LGraph CreateGraph(int vertexNum);
void InsertEdge(LGraph graph, Edge E);
LGraph BuildGraph(int vertexNum, int edgeNum);void UpdateHeap(MinHeap H, int dist[], Vertex V);
Vertex FindMinDist(MinHeap H, int dist[]);
int Prim(LGraph graph, Vertex S);/*
08-图7 公路村村通
难度:2星6 15
1 2 5
1 3 3
1 4 7
1 5 4
1 6 2
2 3 4
2 4 6
2 5 2
2 6 6
3 4 6
3 5 1
3 6 1
4 5 10
4 6 8
5 6 3126 4
1 2 5
1 3 3
1 4 7
5 6 24 4
1 2 10
2 3 20
3 4 30
1 4 404 6
1 2 10
1 3 40
1 4 50
2 3 60
2 4 20
3 4 30607 21
1 2 14
1 3 11
1 4 19
1 5 12
1 6 17
1 7 20
2 3 16
2 4 15
2 5 13
2 6 10
2 7 18
3 4 20
3 5 12
3 6 11
3 7 16
4 5 14
4 6 17
4 7 19
5 6 10
5 7 15
6 7 13*/int main()
{int N, M;scanf("%d %d", &N, &M);LGraph G = BuildGraph(N, M);printf("%d\n", Prim(G, 0));free(G);return 0;
}LGraph CreateGraph(int vertexNum)
{LGraph G;G = (LGraph)malloc(sizeof(struct _LGraph));G->Nv = vertexNum;G->Ne = 0;for (int V = 0; V < G->Nv; V++){G->graph[V].firstEdge = NULL;}return G;
}void InsertEdge(LGraph G, Edge E)
{AdjNode newNode;newNode = (AdjNode)malloc(sizeof(struct _AdjNode));newNode->adjV = E->W;newNode->weight = E->weight;newNode->next = G->graph[E->V].firstEdge;G->graph[E->V].firstEdge = newNode;newNode = (AdjNode)malloc(sizeof(struct _AdjNode));newNode->adjV = E->V;newNode->weight = E->weight;newNode->next = G->graph[E->W].firstEdge;G->graph[E->W].firstEdge = newNode;
}LGraph BuildGraph(int vertexNum, int edgeNum)
{LGraph G = CreateGraph(vertexNum);G->Ne = edgeNum;Edge E;E = (Edge)malloc(sizeof(struct _Edge));for (int i = 0; i < G->Ne; i++){ // 用E->V--,E->W--解决顶点序号从1开始的问题scanf("%d %d %d", &E->V, &E->W, &E->weight);E->V--;E->W--;InsertEdge(G, E);}free(E);return G;
}Vertex FindMinDist(MinHeap H, int dist[])
{Vertex minV = ERROR;// 从堆中取出最小值,并维护最小堆的有效性。minV = DelMin(H, dist);return minV;
}int Prim(LGraph G, Vertex S)
{ // 只计算TotalWeight,无需实际创建生成树WeightType dist[G->Nv], totalWeight;Vertex V;AdjNode W;int vCount;for (V = 0; V < G->Nv; V++)dist[V] = INFINITY;for (W = G->graph[S].firstEdge; W; W = W->next)dist[W->adjV] = W->weight;totalWeight = 0;vCount = 0;dist[S] = 0;vCount++;// 根据dist对未收录顶点创建最小堆MinHeap H = CreateHeap(G->Nv);for (V = 0; V < G->Nv; V++){if (dist[V] != 0){ // H->Elements保存的是未收集顶点的编号,本例依次是1,2,3H->Elements[++H->Size] = V;}}BuildMinHeap(H, dist);while (1){V = FindMinDist(H, dist);if (V == ERROR)break;totalWeight += dist[V];dist[V] = 0;vCount++;for (W = G->graph[V].firstEdge; W; W = W->next){if (dist[W->adjV] != 0){if (W->weight < dist[W->adjV]){ /*目标是调整H->Elements,改了吗?没有,也没有必要H-Elements保存的是顶点。现在要做的是定位到W->adjV对应顶点,做percup*/dist[W->adjV] = W->weight;UpdateHeap(H, dist, W->adjV);}}}}if (vCount < G->Nv) /* MST中收的顶点少于|V|-1个 */totalWeight = ERROR;return totalWeight;
}MinHeap CreateHeap(int MaxSize)
{MinHeap H = (MinHeap)malloc(sizeof(struct _MinHeap));H->Elements = (ELEMENT_TYPE *)malloc((MaxSize + 1) * sizeof(ELEMENT_TYPE));H->Elements[0] = MIN_DATA;H->Size = 0;H->Capacity = MaxSize;return H;
}bool isEmpty(MinHeap H)
{return H->Size == 0;
}bool isFull(MinHeap H)
{return H->Size == H->Capacity;
}ELEMENT_TYPE DelMin(MinHeap H, int dist[])
{if (!isEmpty(H)){ELEMENT_TYPE min, last;int parent, child;min = H->Elements[1];last = H->Elements[H->Size--];for (parent = 1; 2 * parent <= H->Size; parent = child){child = 2 * parent;if ((child != H->Size) && (dist[H->Elements[child]] > dist[H->Elements[child + 1]])){child++;}if (dist[last] <= dist[H->Elements[child]]){break;}else{H->Elements[parent] = H->Elements[child];}}H->Elements[parent] = last;if (dist[min] < INFINITY)return min;elsereturn ERROR;}else{return ERROR;}
}void PercUp(MinHeap H, int p, int dist[])
{ /*根据顶点的dist值,决定顶点在堆中的存储位置。对dist[H->Elements[child]] > dist[H->Elements[child + 1]]的理解dist[x] > dist[y],本质是比较两个顶点之间的dist值,x,y是顶点序号。dist[x]的初始值通过dist[V] = G->dist[S][V]获得,并用dist[W] = dist[V] + G->dist[V][W]更新child是顶点在堆中的索引,H->Elements[child]存储的是顶点序号所以dist[H->Elements[child]]是顶点的dist值。*/int parent, child;ELEMENT_TYPE X;X = H->Elements[p];for (parent = p; 2 * parent <= H->Size; parent = child){child = 2 * parent;if ((child != H->Size) && (dist[H->Elements[child]] > dist[H->Elements[child + 1]])){child++;}if (dist[X] <= dist[H->Elements[child]]){break;}else{H->Elements[parent] = H->Elements[child];}}H->Elements[parent] = X;
}void BuildMinHeap(MinHeap H, int dist[])
{ // p表示顶点在堆中的位置int p;for (p = H->Size / 2; p > 0; p--){PercUp(H, p, dist);}
}void UpdateHeap(MinHeap H, int dist[], Vertex V)
{int i, idx, x;// 找到V在堆中的位置for (i = 1; i <= H->Size; i++){if (H->Elements[i] == V){idx = i;x = dist[H->Elements[idx]];break;}}// 更新V的dist值,并向上调整堆// dist[V] = dist[H->Elements[i]];/* 是否需要条件i>1?*/for (i = idx; i > 1 && dist[H->Elements[i / 2]] > x; i /= 2){H->Elements[i] = H->Elements[i / 2];}H->Elements[i] = V;
}小结:
典型的Prim应用,姥姥没有讲最小堆的具体实现,代码磨了很久,终于过了。简言之,只有对最小生成树算法逻辑有深刻的认识,同时有足够的耐心和细心,实际动手写,才能提高代码能力。
结果:
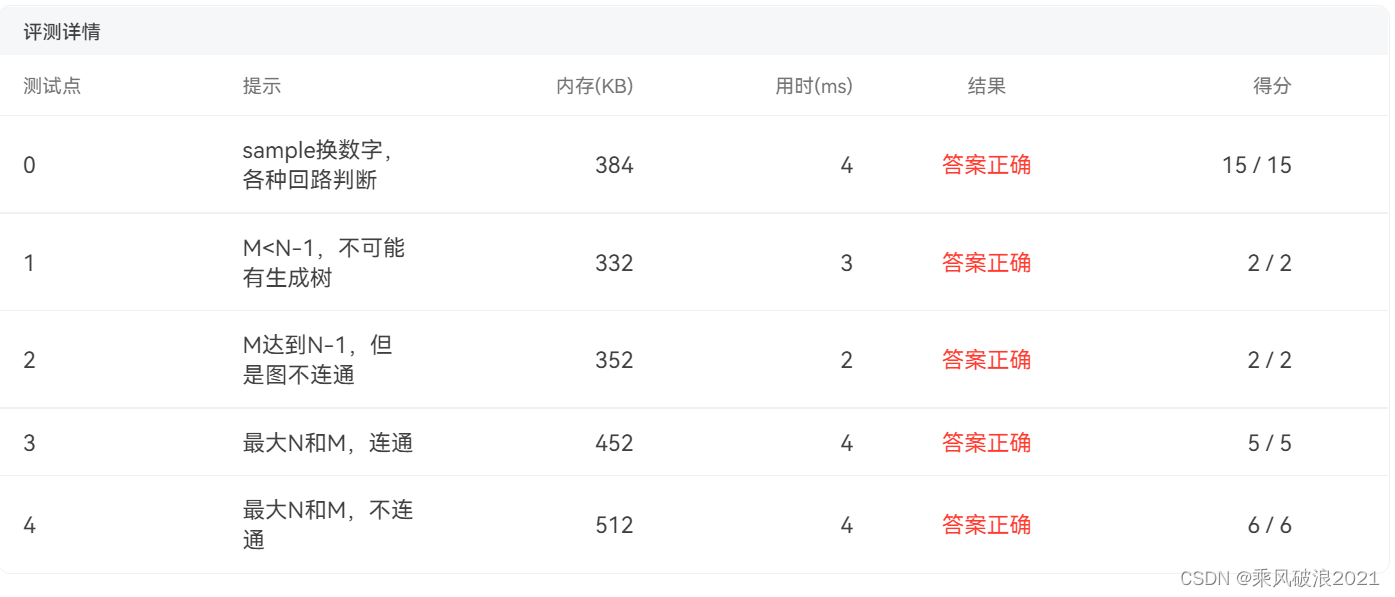
相关文章:

浙大陈越何钦铭数据结构08-图7 公路村村通【循环和最小堆版】
题目 现有村落间道路的统计数据表中,列出了有可能建设成标准公路的若干条道路的成本,求使每个村落都有公路连通所需要的最低成本。 输入格式: 输入数据包括城镇数目正整数N(≤1000)和候选道路数目M(≤3N)…...
Linux 部署1Panel现代化运维管理面板远程访问
文章目录 前言1. Linux 安装1Panel2. 安装cpolar内网穿透3. 配置1Panel公网访问地址4. 公网远程访问1Panel管理界面5. 固定1Panel公网地址 前言 1Panel 是一个现代化、开源的 Linux 服务器运维管理面板。高效管理,通过 Web 端轻松管理 Linux 服务器,包括主机监控、…...

用百度云怎么重装电脑系统
用百度云怎么重装电脑系统 随着云计算技术的飞速发展,百度云成为了人们日常生活中不可或缺的一部分。百度云不仅提供了强大的文件存储和传输功能,还可以帮助人们轻松地重装电脑系统。下面就让我们来介绍一下如何用百度云重装电脑系统。 步骤一…...

SpringCloud环境搭建及入门案例
技术选型: Maven 3.8.4SpringBoot 2.7.8SpringCloud 2021.0.4SpringCloudAlibaba 2022.0.1.0Nacos 2.1.1Sentinel 1.8.5 模块设计: 父工程:SpringCloudAlibaba订单微服:order-service库存微服:stock-service 1.创建…...

什么是序列化和反序列化?
JSON(JavaScript Object Notation)和XML(eXtensible Markup Language)是两种常用的数据交换格式,用于在不同系统之间传输和存储数据。 JSON是一种轻量级的数据交换格式,它使用易于理解的键值对的形式表示数…...

React 消息文本循环展示
需求 页面上有个小喇叭,循环展示消息内容 逻辑思路 设置定时器,修改translateX属性来实现滚动,判断滚动位置,修改list位置来实现无限滚动 实现效果 代码 /** Author: Do not edit* Date: 2023-09-07 11:11:45* LastEditors: …...
java获取jenkins发布版本信息
一.需求: 系统cicd发布时首页需要展示jenkins发布的版本和优化内容 二.思路: 1.jenkins创建用户和秘钥 2.找到对应构建任务信息的api 3.RestTemplate发起http请求 三.实现: 1.创建用户和token 2.查找jenkins API 创建 Job POST http://localhost…...
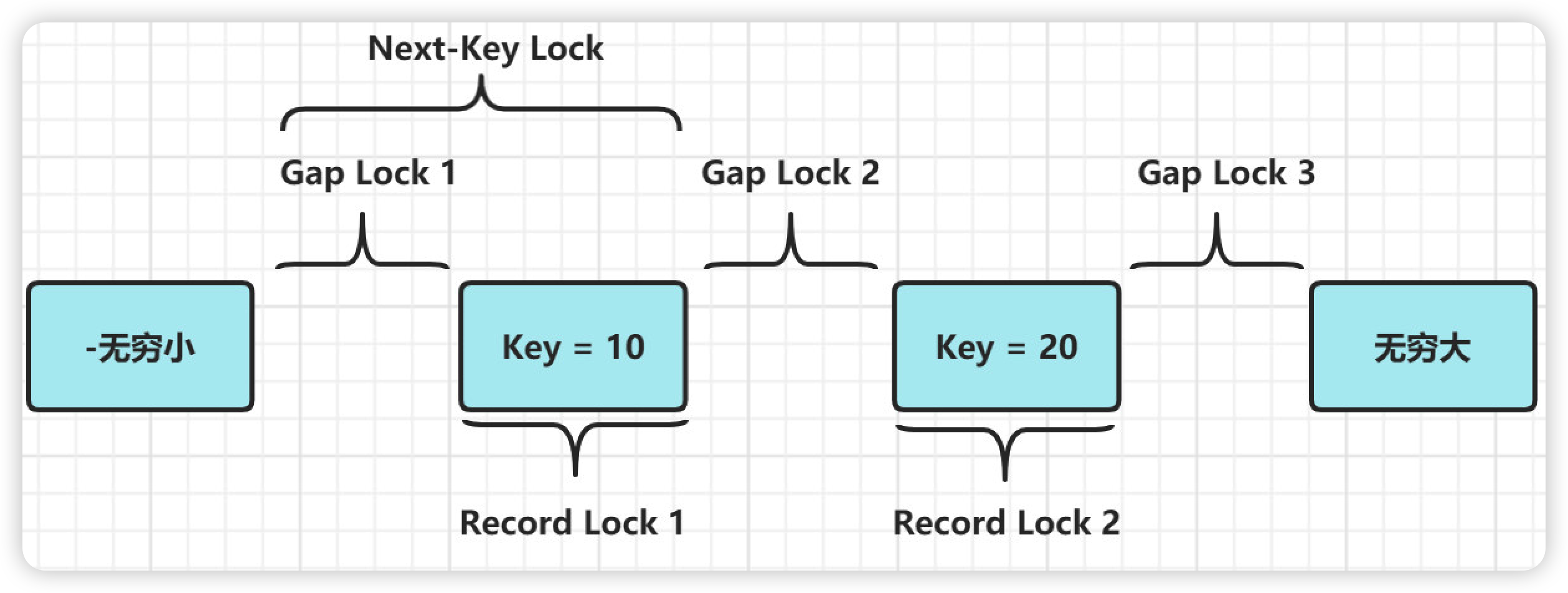
java八股文面试[数据库]——可重复读怎么实现的(MVCC)
可重复读(repeatable read)定义: 一个事务执行过程中看到的数据,总是跟这个事务在启动时看到的数据是一致的。 MVCC MVCC,多版本并发控制, 用于实现读已提交和可重复读隔离级别。 MVCC的核心就是 Undo log多版本链 …...

cl 和 “clangtidy“分别是什么?是同一样东西吗?
作者:gentle_zhou 原文链接:cl 和 "clangtidy"分别是什么?是同一样东西吗?-云社区-华为云 先说结论:这两个是不同的工具,cl是编译器,clangtidy是代码检查工具,它们不是一…...

ubuntu22.04开机自启动Eureka服务
ubuntu22.04开机自启动Eureka服务 1、创建启动脚本eurekaService.sh #我们把启动脚本放在/usr/software目录下 cd /usr/software vim eurekaService.sheurekaService.sh内容为 #!/bin/sh # this is a eurekaService shell to startup at the mechian power on.echo "eu…...

【 OpenGauss源码学习 —— 列存储(analyze)(三)】
列存储(analyze) acquire_sample_rows 函数RelationGetNumberOfBlocks 函数BlockSampler_Init 函数anl_init_selection_state 函数BlockSampler_GetBlock 函数ReadBufferExtendedPageGetMaxOffsetNumber 函数HeapTupleSatisfiesVacuum 函数heapCopyTuple…...

Element Plus table formatter函数返回html内容
查看 Element Plus table formatter 支持返回 类型为string 和 VNode对象; 若依全局直接用h函数,无需引用 下面普通基本用法:在Element Plus中,你可以使用自定义的formatter函数来返回VNode对象,从而实现更灵活的自定…...

c++ mutable
mutable 可变的,易变的 跟 constant(既C中的const)是反义词作用: 保持常量对象中大部分数据成员仍然是“只读”的情况下,实现对个别数据成员的修改使类的const函数可以修改对象的mutable数据成员。 注意事项ÿ…...
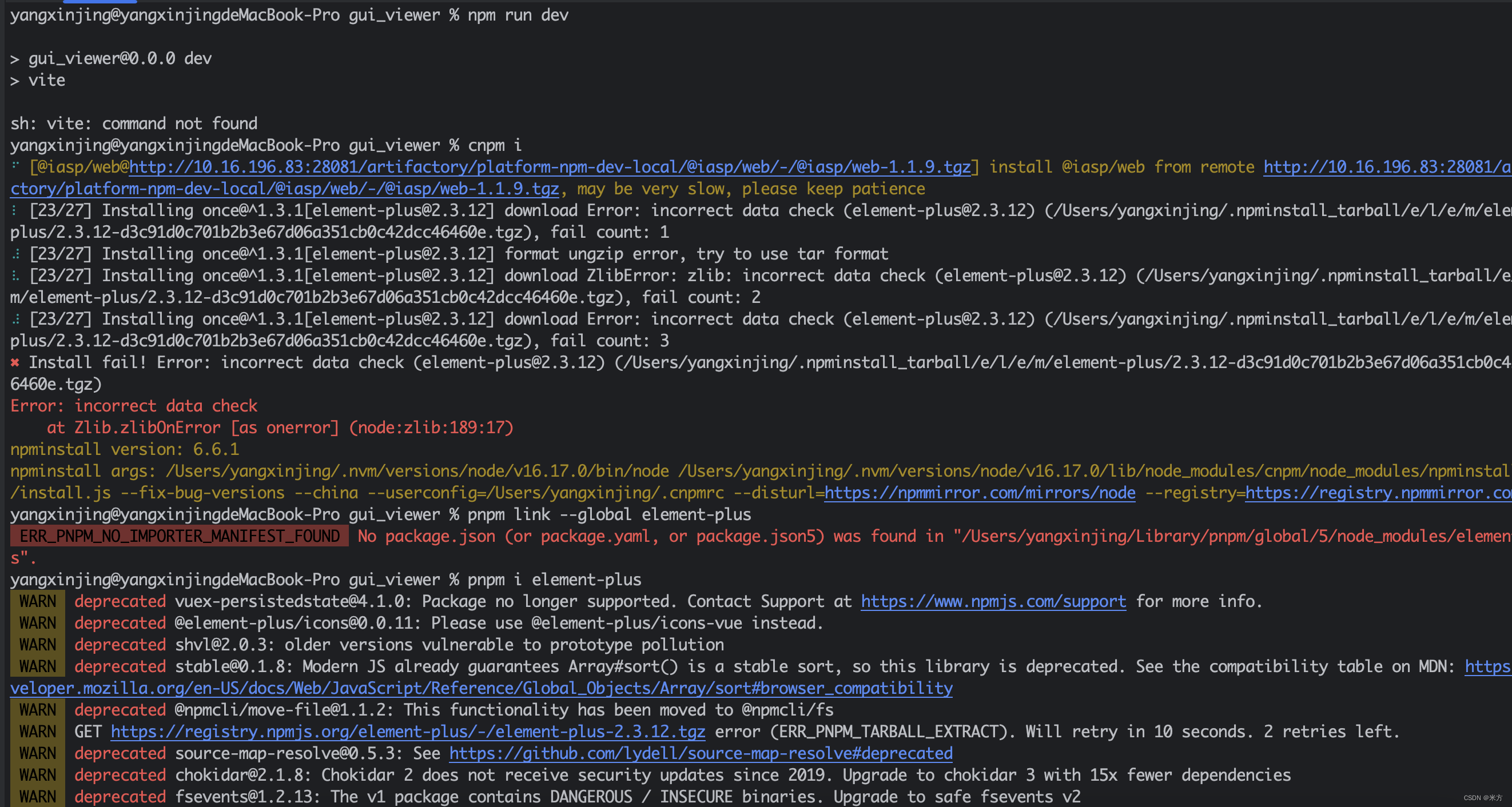
element-plus 踩的坑
原来node版本是16.17.0,装element-plus死活装不上,结果要把node版本升级到18以上,真坑呀,也没人告诉我要这么干...

Python、Rust中的协程
协程 协程在不同的堆栈上同时运行,但每次只有一个协程运行,而其调用者则等待: F启动G,但G并不会立即运行,F必须显式的恢复G,然后 G 开始运行。在任何时候,G 都可能转身并让步返回到 F。这会暂停 G 并继续…...
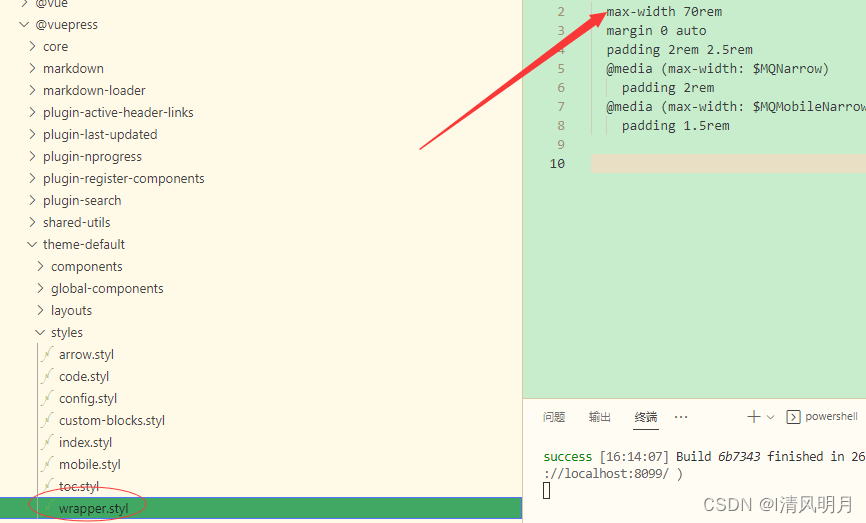
Vuepress样式修改内容宽度
1、相关文件 一般所在目录node_modules\vuepress\theme-default\styles\wrapper.styl 2、调整宽度,截图中是已经调整好的,在我电脑上显示刚刚好。...
Vue2电商前台项目——项目的初始化及搭建
Vue2电商前台项目——项目的初始化及搭建 Vue基础知识点击此处——Vue.js 文章目录 Vue2电商前台项目——项目的初始化及搭建一、项目初始化1、脚手架目录介绍2、项目的其他配置 二、项目的路由分析及搭建1、项目的路由分析2、开发项目的步骤3、非路由组件的搭建4、路由组件的搭…...

递归算法学习——N皇后问题,单词搜索
目录 编辑 一,N皇后问题 1.题意 2.解释 3.题目接口 4.解题思路及代码 二,单词搜索 1.题意 2.解释 3.题目接口 4.思路及代码 一,N皇后问题 1.题意 按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上…...

【SpringBoot】mockito+junit 单元测试
1.POM 引入以下依赖 <dependency><groupId>junit</groupId><artifactId>junit</artifactId><version>4.13.2</version><scope>test</scope></dependency><dependency><groupId>org.springframework.b…...
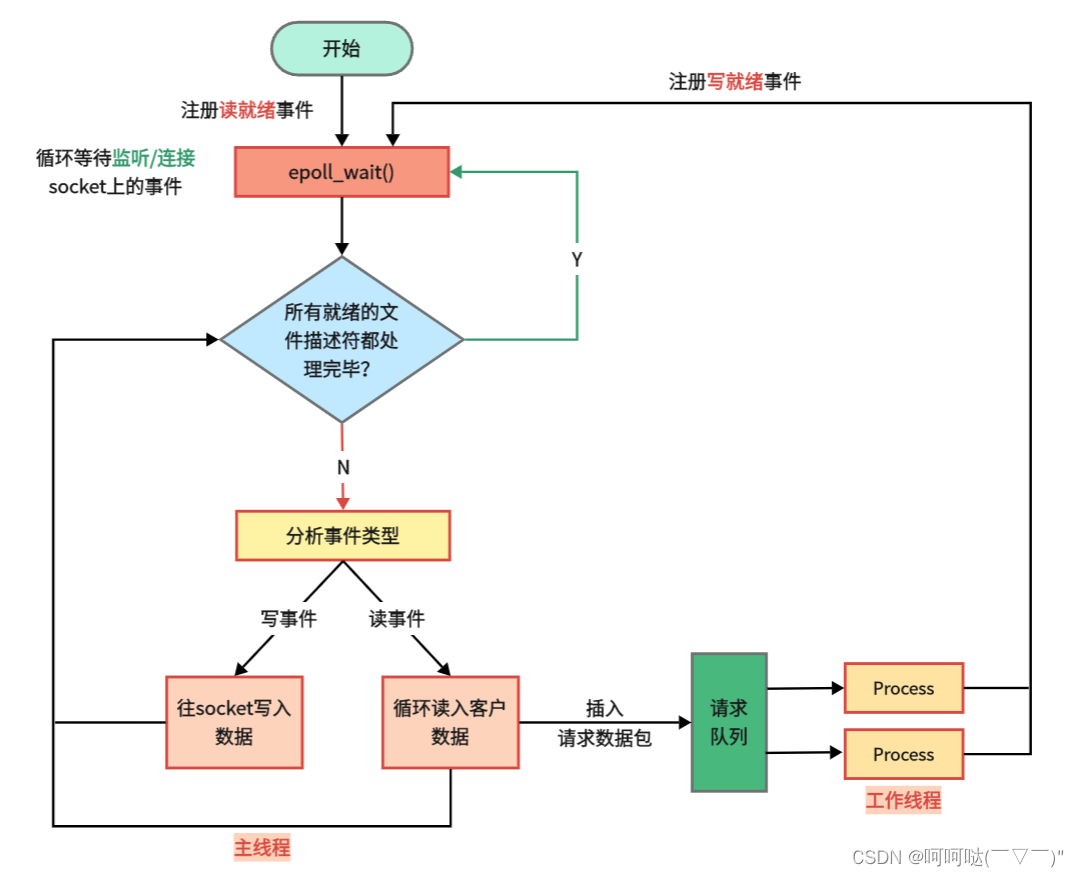
webserver 同步 I/O 模拟 Proactor 模式的工作流程
服务器基本框架、I/O 模型、事件处理模式 一、服务器编程基本框架 虽然服务器程序种类繁多,但其基本框架都一样,不同之处在于逻辑处理。 二、五种 I/O 模型 阻塞/非阻塞、同步/异步(网络IO)_呵呵哒( ̄▽ ̄)&…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...
